惯性辅助的GNSS可区分性分析和粗差探测方法研究

吴有龙,陈 帅

(1.金陵科技学院 电子信息工程学院, 南京 211169;2.南京理工大学 自动化学院, 南京 210094)

0 引言

全球导航卫星系统(global navigation satellite system,GNSS),如全球定位系统(global positioning system,GPS)、全球导航卫星系统(global navigation satellite system,GLONASS)和北斗卫星导航系统(beidou navigation satellite system,BDS),目前在世界各地广泛使用,并成为交通运输、民用和军用飞机、航空摄影测量、无人机和移动测绘系统高精度定位共性基础[1-3]。

GNSS提供的位置和速度解不受误差积累的影响。然而,在信号退化环境中,卫星信号很容易受到建筑物的遮挡,阻塞和干扰[4]。对于城区环境下导航应用,接收机接收到的信号强度通常比实际开放环境水平低10～30 dB。此外,GNSS接收机通常无法估计用户的姿态且动态环境下性能差。相比之下,惯性导航系统(inertial navigation system,INS)不受外界阻塞和干扰,具有较强的动态适应能力且支持姿态估计[5]。然而,INS存在误差积累的问题。所有类型的惯性传感器都存在一定程度的零偏、尺度因子、交叉耦合误差和随机噪声等。因此,当使用INS进行导航时,需要通过外部辅助信息对其进行标定和对准[6]。

GNSS和INS紧组合具有良好的互补特性,可以取得比单系统更好的性能,提供了一个连续完整的导航解,具有很高的长期和短期精度[7-8]。此外,与松组合和深组合相比,紧组合实现了效率和性能之间的平衡,因而得到了广泛应用。然而,由于导航传感器的观测存在各种不确定因素的干扰,组合后的导航信息并不总是可靠、准确的。如果不及时探测和剔除粗差,将直接影响组合导航的精度[9-13]。因此,实时粗差探测、识别和剔除对于保证组合导航系统的可靠性和精度具有重要意义。

粗差探测功能提供故障告警能力,保证系统的完好性;粗差识别功能是提供排除故障测量的能力,提高系统的连续性。粗差探测和识别有两类处理方法,一类是将粗差归纳为函数模型,进行粗差探测和识别,一类是将粗差归类为系统随机模型,利用权函数处理策略,进行抗差估计。针对单GNSS系统,文献[14]对数据探测法、部分最小二乘法等几种粗差探测法的观测值相互独立及相关时的可靠性进行了深入比较分析,对比了最小边界误差的效果;文献[15]通过理论和数值计算证明了测量中数据探测法中误警、漏检和误判与观测量之间相关,误判严重影响系统的可靠性。文献[16]研究了BDS/GPS组合定位可靠性分析与粗差探测,对比了包含单粗差和双粗差的单系统和双系统粗差探测成功率和识别率。针对GNSS/INS组合导航系统的3种组合模式,相关学者开展了多方面研究。文献[17-19]对松组合的抗差方法进行了研究,主要利用残差来构造统计量,通过加权因子来调节滤波矩阵,降低粗差对状态估计的影响;文献[20-22]对紧组合抗差方法进行了研究,对卫星几何分布的不佳情况下的抗差方法和不同类型故障进行了讨论分析;文献[23]探讨了深组合粗差探测与剔除方法,提出了利用预滤波器的输出和积分滤波器的估计构造检验统计量,来进行突变粗差和缓变粗差的探测和隔离。

虽然已有文献对测量领域的数据探测法中的粗差误判、可靠性理论以及相关性进行了分析,但都是基于单GNSS或者多GNSS系统进行研究的;对GNSS/INS组合导航系统的粗差探测方法主要是将粗差归纳为随机模型,利用抗差方法进行分析,不进行粗差探测和识别。为此,本文中详细讨论惯性辅助GNSS的可靠性理论,分析粗差可区分性,粗差探测和识别准确率,并比较分析不同情况下的定位结果。

1 GNSS/INS紧组合导航系统模型

紧组合导航系统状态误差方程由INS和GNSS状态组成。惯导误差方程采用“东北天”当地坐标系(n系)下的psi角误差方程,系统共包含17个状态向量,分别为3个位置状态,3个速度状态,3个姿态状态,3个加速度计零偏,3个陀螺零偏,1个接收机钟差和1个接收机钟漂,状态方程如下[17,21,24]:

(1)

GNSS/INS系统状态模型是基于17状态扩展卡尔曼滤波(extended kalman filter,EKF)方程展开的,在假设高斯分布噪声的非线性系统模型上进行一阶线性化的,式(1)在历元k离散化的状态模型为[20,22-23]:

xk=Φk-1xk-1+wk-1

(2)

式中:xk为状态矢量;Φk-1为状态转移矩阵;wk-1为方差是Qk-1的系统白噪声。

观测模型由GNSS伪距观测值与INS推算预测伪距差组成。GNSS伪距矢量ρGi和预测伪距矢量ρIi的简化数学模型如下[20,22-23]:

(3)

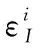
采用闭环反馈校正方式进行组合导航,以INS和GNSS的输出的伪距之差作为滤波器的观测量,观测方程为[20,22-23]:

δρ=ρIi-ρGi

(4)

因而,当观测到m颗卫星,对应的离散卡尔曼滤波观测方程为[20,22-23]:

zk=Hkxk+εk

(5)

式中:zk为观测向量;Hk为观测矩阵;εk为方差是Rk观测噪声。

2 GNSS/INS完好性基本原理

(6)

式中:lk为观测向量;Ak为设计矩阵;vk为残差向量,且[19,24]

(7)

相应的估计残差及其协方差矩阵为:

(8)

粗差探测检验是一种二元假设检验。组合导航系统中,根据残差及其协方差矩阵,构建方差因子统计量γk,即[19,24]

(9)

假设观测量中只存在单个粗差,采用数据探测法进行粗差识别。第i个观测量的检验统计量构造为[14-16,19]:

(10)

式中,hi=[0…1…0]T为第i个元素为1,其他元素为0的单位化向量。当该观测值上无粗差时,原假设成立,即wi～N(0,1),检验统计量wi≤TD=μ1-α/2,其中,TD为门限阈值,μ1-α/2为显著水平对应的标准正态分布的分位值;若存在粗差,则备选假设成立,即wi～N(λ0,1),检验统计量wi>TD,λ0为非中心化参数。α为显著水平,本文中α=0.1%,因此对应的TD=3.291。

内部可靠性是指在一定的假设检验条件下系统发现粗差的能力,用最小可探测粗差(minimum detective bias,MDB)来衡量[14-16,19]:

(11)

式中,λ0=u1-α/2+u1-β,β为检验功效。本文中1-β=20%,因此对应的λ0为4.13。

由于不同的观测量的统计量是相关的,当只有1个粗差观测量时,可以同时检测到几个粗差检验统计量大于阈值。因此,定位粗差的位置是很困难的,必须考虑观测量之间的可区分性。2个检验统计量之间的相关系数如下[15-16,19]:

(12)

式中,|ρij|≤1。理论上,当只有5颗卫星时,任意两两观测值之间的相关系数都为1,即完全相关,无法进行粗差区分。同等观测条件下,随着卫星数量的增加,卫星观测值之间的相关系数减小,将增大粗差的可区分性。反之,随着卫星数量的减少,观测值之间的可区分性将减小,发生在这两观测值上的粗差就越难被区分。

3 计算与分析

为了对所提出的粗差探测和识别方案进行验证,建立了基于EKF的紧组合GNSS/INS系统仿真平台。图1为模拟运动轨迹,运行时间共4 476 s。根据参考运动的轨迹、速度和姿态,计算出无噪声的传感器测量值。然后,模拟加入传感器零偏和白噪声原始的观测量,噪声参数按照战术级INS进行设计。仿真过程中共35颗卫星,包括5颗地球静止轨道卫星,3颗倾斜地球同步轨道卫星和27颗中圆地球轨道卫星。传感器参数和GNSS参数如表1所示。城市环境中经常出现信号严重遮挡,图2为模拟遮挡环境下的卫星分布天空可视图,其中方位角[45°-135°]和[225°-315°]方向的卫星被完全遮挡,可见卫星的编号为[01,07,08,14,19,20,21,29,30]。

表1 传感器参数

图1 模拟运行轨迹Fig.1 Simulated running trajectory

图2 卫星天空可视图Fig.2 Sky plots of satellites

图3为整个运动过程中可见星数和位置精度因子(position dilution of precision,PDOP)值随时间变化情况,可见卫星为5～8颗。在2 373～3 588 s时间段,可见卫星数最少,仅为5颗,由于遮挡环境下卫星的空间几何分布差,造成PDOP值在10～14变化,将使得这段时间内定位精度较差。

3.1 单个历元相关系数和内部可靠性分析

图4为500、1 500、2 000和2 500 s四个历元单GNSS系统和GNSS/INS组合导航系统卫星观测值之间的相关性关系,4个观测历元对应的分别有8、7、6和5颗可见卫星。单GNSS系统,5颗卫星时,各观测量之间是完全相关的,相关系数都为1,随着可见卫星数的增加,各观测量之间的相关性变低,但也存在观测值之间的相关性比较高的情况;而GNSS/INS组合导航系统,所有观测值之间的相关性显著降低,基本都小于0.2。以2 000 s历元为例,可见卫星有6颗,表2和表3分别为单GNSS系统和GNSS/INS组合导航系统的观测统计量之间的相关性数值,单GNSS系统有(2,3),(2,5)和(5,6)两两观测统计量之间的相关系数分别为0.987、0.976和0.933;当GNSS/INS组合以后,两两观测量之间的相关系数分别为0.188、0.132和0.213。

图3 可见卫星数和PDOP值Fig.3 Number of visible satellites and PDOP values

表2 历元2 000 s 单GNSS系统相关系数矩阵

表3 历元2 000 s GNSS/INS组合相关系数矩阵

表4为单GNSS系统和GNSS/INS组合导航系统对应4个历元观测量最小可探测粗差下界值。单GNSS系统,随着观测卫星的减少,各卫星之间的几何结构变差,最小可探测粗差值变大,其中19号卫星在整个观测过程中都可见,最小可探测粗差持续变大,分别为5.507、6.058、6.177和 19.201 m。当只有5颗卫星时,30号卫星的最小可探测粗差达到 2 812.279 m。GNSS/INS组合能够有效改善各观测量之间的相关性,观测卫星的数量和几何结构对可探测粗差影响较小,可探测粗差的下界值在4.4～4.7 m,总体比较平稳,便于系统探测出粗差。

图4 4个历元卫星之间的相关系数Fig.4 Correlation coefficients between satellites in four epochs

表4 单历元GNSS单系统和GNSS/INS组合导航系统的MDB值(m)

3.2 多历元相关性和内部可靠性分析

以19号卫星为例,对各个历元的内部可靠性以及相关性进行解算。整个观测阶段GNSS和GNSS/INS组合可靠性结果如图5所示。2 373～3 588 s和3 884～4 476 s阶段,只有5颗可见卫星,可见卫星的减少直接导致PDOP值增大,造成在这个阶段MDB值异常大,可探测粗差的下界值为16.57～8 821 m。0～1 300 s,1 301～1 643 s和3 589～3 883 s三个阶段,最小可探测粗差为5.419～6.732 m。图5为GNSS/INS组合的MDB值,最大值为5.593 m,最小值为4.482 m,均值为4.643 m。

图5 GNSS和GNSS/INS组合可靠性结果Fig.5 MDB of GNSS and GNSS/INS integration

图6为各卫星与19号卫星之间的最大相关系数。由图可知:对于单GNSS系统,0～1 300 s阶段可见卫星数为8,卫星的相关系数基本都小于0.6。7颗卫星时卫星相关系数为0.85左右。5颗卫星之间完全相关,相关系数都为1;1 644～2 372 s和3 589～3 883 s两个阶段可见卫星数为6。相关性大于0.95,特别在3 589～3 883 s阶段相关性都接近1。当INS辅助GNSS,各阶段卫星之间的观测量之间相关性显著降低,相关系数在0.3左右,能够有效地进行粗差识别,个别历元由于运动轨迹有机动转弯,存在大的机动性,状态模型导致相关系数偏大。

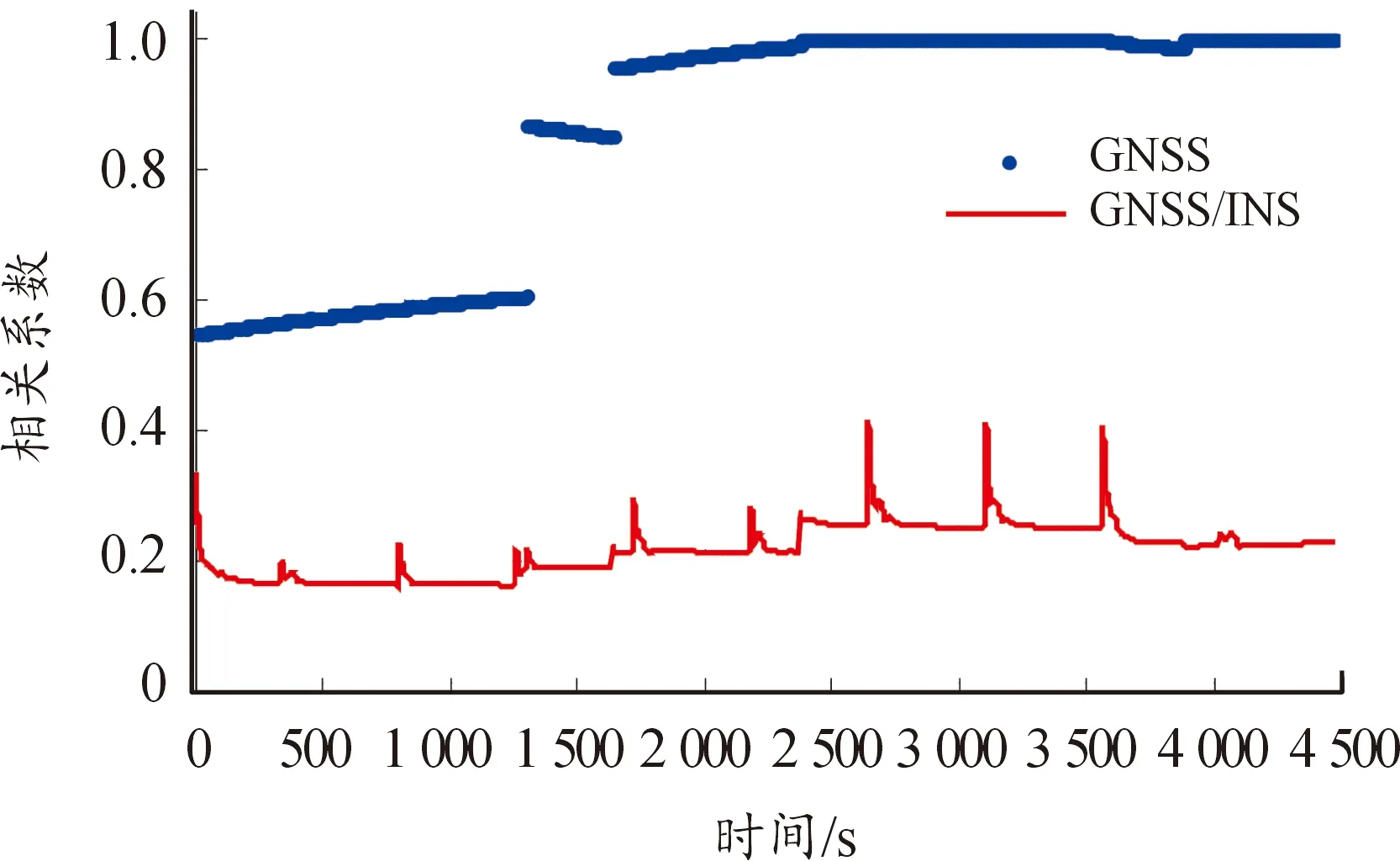
图6 各卫星与19号卫星之间的最大相关系数Fig.6 Maximum correlation coefficient between each satellite and satellite 19

3.3 粗差探测识别和定位结果分析

当有5颗可见卫星,卫星之间相关性为1,单GNSS系统只能进行粗差探测,而不能进行粗差识别,故不对5颗卫星加入粗差进行分析。当观测卫星数大于5,对19号卫星上加入一个15 m的粗差。图7给出了粗差探测的卡方检验的统计量结果,粗差探测的阈值随观测卫星的数变化而不同,单GNSS系统检测阈值为3.715～7.879,GNSS/INS组合粗差探测阈值为3.484～4.421。图中显示加入粗差的几个阶段统计量都超过阈值,探测出存在粗差。图8给出了粗差识别的数据探测法w统计量结果。从图中可知各个历元都能有效地识别出粗差,统计量都大于阈值3.291,其中统计量的最大值即对应粗差的位置。

图7 粗差探测统计量Fig.7 Outlier detection statistics

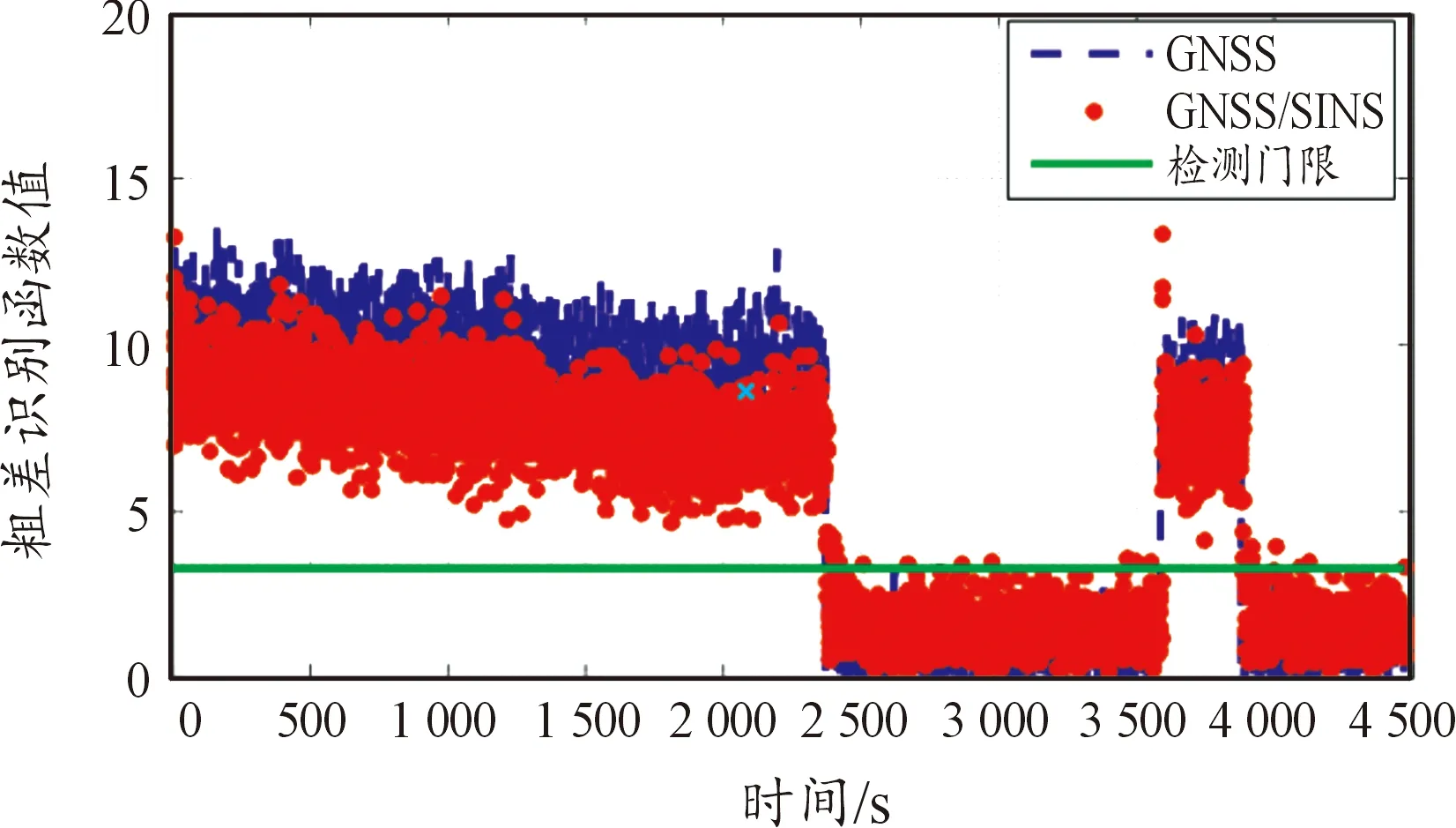
图8 粗差识别统计量Fig.8 Outlier identification statistics

图9和图10分别为单GNSS系统和GNSS/INS组合导航系统加入粗差和剔除粗差的定位结果。对于所有观测历元,GNSS/INS组合导航系统均能够准确识别粗差并剔除,定位精度高。0～1 300 s和1 301～1 643 s阶段可见星数分别为8和7,19号卫星与其他卫星之间的相关性不强,当加入15 m粗差,单GNSS系统能正确探测和正确识别粗差,剔除粗差后定位精度较高。在2 373～3 588 s和3 884～4 476 s阶段,探测粗差存在,但是由于相关性强,单GNSS系统在多个历元无法正确识别粗差的位置,导致定位性能急剧下降。

图9 单GNSS系统粗差探测和剔除定位误差Fig.9 Positioning errors of adding the outliers and excluding the outliers in single GNSS system

图10 GNSS/INS组合粗差探测和剔除定位误差Fig.10 Positioning errors of adding the outliers and excluding the outliers in GNSS/INS integrated system

表5给出了单GNSS系统和GNSS/INS组合导航系统解算结果,包括未加入粗差、加入粗差和剔除粗差3种模式的定位精度统计表。单GNSS系统未加入粗差东、北、天方向定位精度分别为1.654、1.369、6.384 m,加入粗差后定位精度分别下降为6.604、4.938、6.669 m,3个方向上定位精度分别下降了74.95%、72.28%、4.27%,剔除粗差定位精度分别下降72.73%、71.50%、47.82%。剔除粗差和加入粗差的定位结果在水平方向上相当,天向定位精度反而更差,这是由于两向遮挡环境下天向精度因子差,剔除一个观测卫星后,导致卫星空间几何结构更差,从而导致定位结果出现较大的偏差。GNSS/INS组合导航系统未加入粗差东、北、天方向定位精度分别为0.473、0.332、1.093 m;加入粗差后定位精度分别下降91.64%、92.70%、55.22%;所有历元都能准确探测和识别粗差,剔除粗差后3个方向上定位精度分别为0.634、0.451、1.148 m,精度下降了25.39%、26.39%、4.79%;而剔除粗差后相对于加入粗差的精度提高了88.79%、90.09%、52.97%。通过惯性辅助GNSS,没有误判的情况发生,定位精度得到了显著提升,惯性辅助GNSS剔除粗差后的定位精度相对单GNSS系统分别提高了89.55%、90.61%、90.62%。

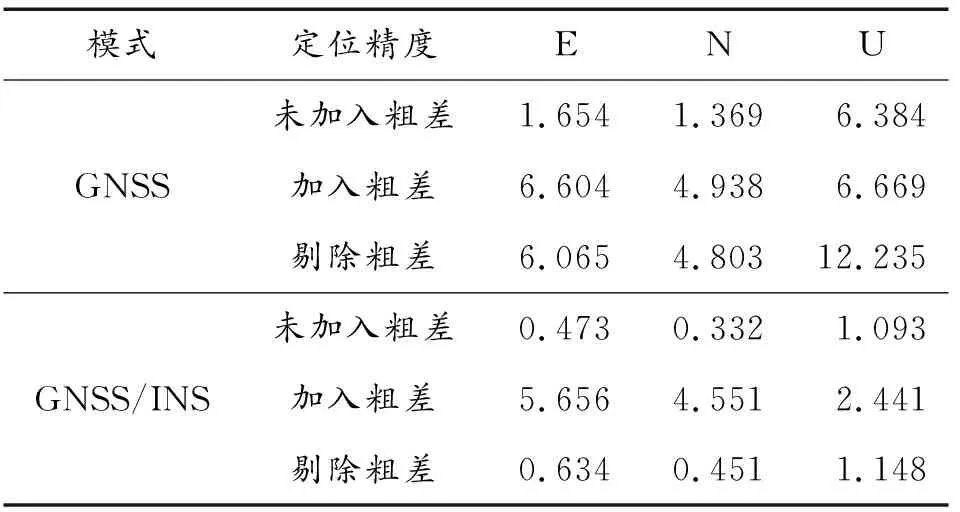
表5 定位精度(RMS)统计(m)

当观测卫星数为6,观测值之间表现为强相关性,对19号卫星分别加入10、15、20和30 m的粗差,对比分析单GNSS系统和GNSS/INS组合导航系统2种模式粗差探测和识别的效率。由表6可知,2个时间段分别加入729个和295个粗差,随着加入粗差值变大,单GNSS系统错误识别率变低。在1 644～2 372 s阶段,加入了10 m粗差,错误识别率达到了63.65%,而随着加入粗差增大,错误定位粗差率逐渐降低,分别降低至18.24%、8.64%和1.78%。3 589～3 883 s阶段,随着加入的粗差增大,错误识别率分别为73.56%、66.78%、60.34%和44.07%。对比2个时间阶段,都只有6颗观测卫星,同样大小的粗差,导致3 589～3 883 s阶段的错误定位粗差率明显高于1 644～2 372 s阶段,这是由于后一阶段观测量之间的相关性大于前一阶段,甚至接近于1,从而导致单GNSS系统误判率高。当惯性辅助GNSS进行粗差探测和识别,使得观测量之间的相关性降低,系统都能准确地进行粗差探测并且识别正确率达到100%。

表6 粗差探测和识别结果

4 结论

1) 受限观测环境下,单GNSS系统最小可探测粗差值存在异常大的情况,惯性辅助GNSS系统能够有效降低最小可探测粗差的值,且最小可探测粗差值稳定。

2) 观测卫星为5颗时,单GNSS系统由于观测量相关性为1而无法区分粗差;惯性辅助GNSS系统能够将统计量间相关性降低至0.2左右,有效弥补了可见卫星数目不足导致强相关性的问题,实现了正常探测和识别粗差。

3) 观测卫星大于6颗时,单GNSS系统在进行粗差探测和识别时无法避免由于卫星相关性较高而引起的粗差误判问题;惯性辅助GNSS系统可有效提高粗差探测和识别的正确率,保障了受限环境下的导航精度。