电磁同步线圈推进过程中动态力学状态分析

李 伟,李首德,刘世亮,熊 玲,程军胜

(1.北京石油化工学院 信息工程学院, 北京 102617; 2.中国科学院电工研究所, 北京 100190)

0 引言

电磁推进技术是将电能转化为电磁能、利用电磁力将物体推进到指定速度的现代化推进技术。随着科学技术的快速发展,国内对电磁推进器的研究热情日益高涨[1]。电磁同步线圈推进器为众多电磁推进器中的一种,它具有效率高、推进质量范围大和受控性好等优点,在推进技术领域拥有广阔的应用前景[2-4]。

电磁同步线圈推进器是利用控制系统触发电源放电,电流经过初级线圈瞬间会产生几十个特斯拉的磁场。电枢在磁场的作用下产生涡流与磁场相互作用,该作用会对电枢产生向前的推力,从而使电枢做加速运动,达到推进电枢的效果[5-8]。由于初级线圈在通入脉冲电流的瞬间产生强磁场,在对电枢产生推进作用的同时会对电枢产生很强的径向挤压力,可能会引起电枢发生变形,导致电枢及内部元件损坏[9-11],同时强电磁力会对线圈本身产生非常大的力学冲击,电磁力过大不仅会影响推进器的寿命,还会导致推进器绝缘固定外壳损坏引起线圈短路,存在爆炸的风险[12-13]。

为避免出现因电磁力过大而导致的推进器使用周期缩短、电枢形变和安全性等问题,提高推进器的可靠性,本研究中以电磁同步线圈推进器为研究对象,采用COMSOL有限元分析软件对电磁同步线圈推进过程中电枢和初级线圈在不同时刻的磁场、电流密度、应力和形变量等物理量分布状况进行了仿真分析。结合电磁同步线圈推进器的有限元仿真分析和试验验证结果,提出了更为合理的同步电枢结构优化设计方案,为高稳定性、高结构强度和轻质量的电枢设计提供理论依据和参考。

1 电磁同步线圈推进过程中数理方程

1.1 推进器模型

电磁同步线圈推进器的推进系统主要由初级线圈、推进物体和绝缘固定外壳组成[14],其中推进物体主要包含电枢和绝缘配重块。由于推进器为轴对称结构,且在推进过程中只需考虑物理量在轴向和径向的变化,不考虑切向的变化,为了简化模型,采用二维轴对称模型进行仿真,并忽略绝缘配重块质量以外因素对推进过程中的影响。同步线圈推进轴对称简化模型如图1所示,绝缘固定外壳的底部为参考平面,以z轴为对称轴,电枢运动方向为z轴正方向,图1中z=40代表电枢的初始位置、z=20代表初级线圈距离底部的高度,表1为推进器的详细参数。

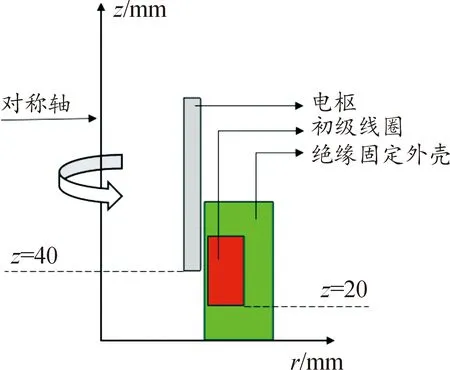
图1 推进器轴对称简化模型

表1 电磁同步线圈推进器参数

1.2 电枢受力分析

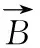
图2 电枢局部位置受力分析图

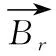
(1)

同理电枢在径向上所受电磁力为沿径向向里,受力为

(2)

1.3 数理分析

电磁同步线圈推进原理如图3所示,驱动线圈为初级,电枢为次级。假设初级线圈为1组串联线圈,次级线圈为多个独立的电感电阻回路。初级线圈由大功率脉冲电容器供电,在推进器内产生脉冲磁场,次级线圈在变化磁场中感应出不同强度的感应电流,电枢感应出的电流在原脉冲磁场的作用下运动起来。

图3 电磁同步线圈推进器原理图

从电枢整体来看,由于同步线圈推进器的内部磁场为轴向磁场,在电枢表面产生的电流以环向为主,少有径向电流,因此,在理论推导的过程中只考虑电枢的环向电流,将电枢看作多个电流环组成,每个电流环视为一个单匝线圈,在电路中等效为一个闭合电感和电阻回路,并依据感应电流分布特性,将电枢分为多个两层单匝分体电枢[15],分体电枢模型图如图4所示。

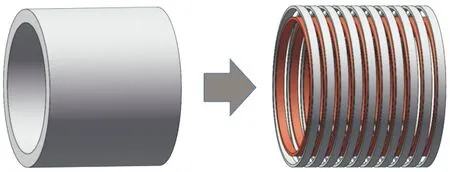
图4 分体电枢模型

分体电枢模型中每个分体电枢可视为独立的电流环,不存在直接的电接触,只存在互感。初级线圈由多匝线圈串联组成的,线圈电流相同且线圈间存在互感。其中初级线圈与分体电枢之间的互感大小为:

Msd=φsd/Id

(3)

初级线圈间的互感大小为

Mdd=φdd/Id

(4)

分体电枢间的互感大小为

Mss=φss/Is

(5)

初级线圈与分体电枢依据基尔霍夫电压定律可以列驱动回路时域电压方程为

(6)

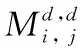
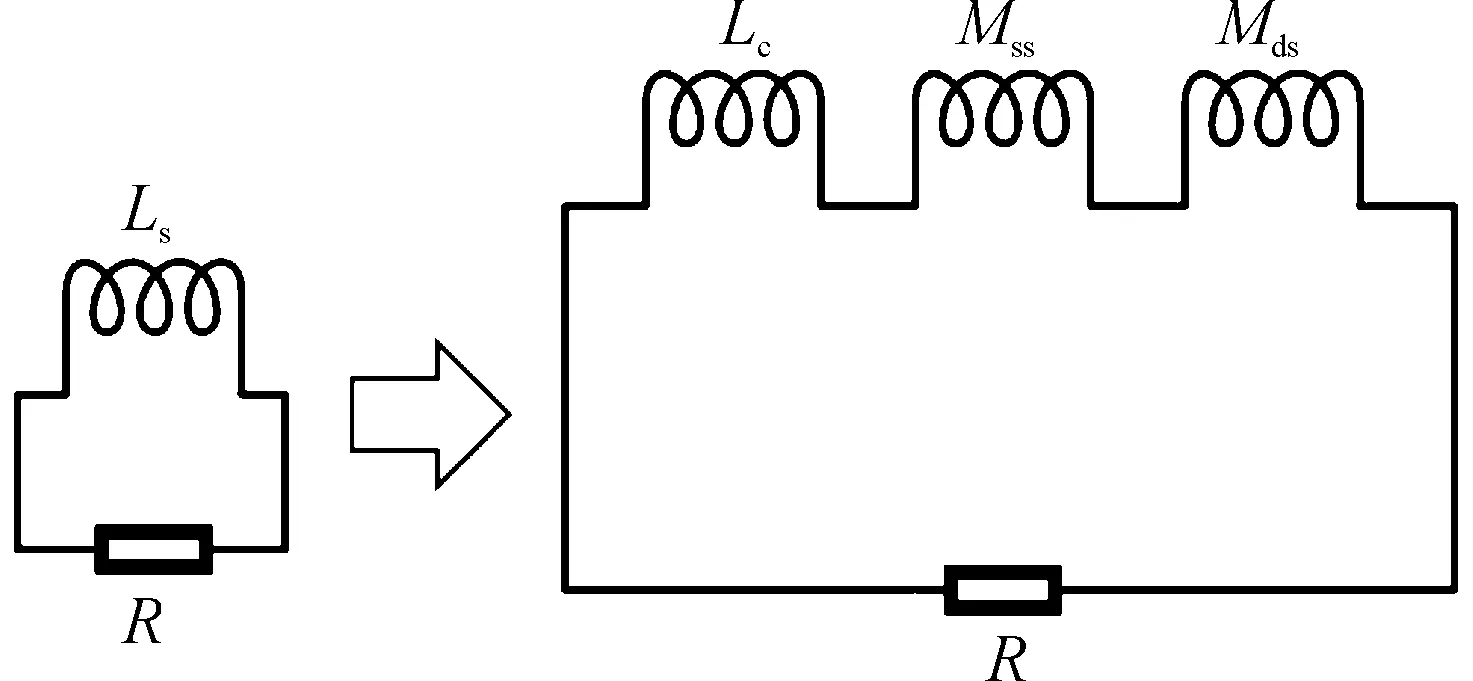
图5 分体电枢原理示意图

分体电枢由电感(Ls)和电阻(rs)组成,其中电感由分体电枢自感(LC)、分体电枢与初级线圈间的互感(Mss)和分体电枢与其余分体电枢互感(Mds)组成,电枢原理图如图5所示,电枢的驱动电压为感应电动势,因此每个分体电枢的基尔霍夫电路方程为

(7)

在推进过程中,第i个分体电枢的轴向受力大小为:

(8)

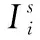
为求解初级线圈在分体电枢上产生的磁场径向分量Br,设分体电枢在z0处为高为Δz半径为r的圆柱闭合面,底面面积为A1,顶面面积为A2,侧面面积为Ar,分体电枢磁场径向分量计算模型如图6所示,其中圆柱面的磁通φt为:

(9)

互感公式定义为:

M=φ/i

(10)

初级线圈在z0位置以及z0+Δz位置与分体电枢的互感值之差,结合式(9)和式(10)可得:

M(z0+Δz)-M(z0)=

(11)

当Δz很小时,圆柱面的底面磁通与顶面磁通可视为相等,化简可得:

(12)

图6 分体电枢磁场径向分量计算模型

(13)

此时,电枢位置的径向磁通密度大小为:

(14)

其中,dM/dz为初级线圈与分体电枢的互感梯度,结合式(8)某一片分体电枢受到单匝初级线圈的轴向推力大小为:

(15)

因此,电枢的轴向推力大小为

(16)

同理,初级线圈产生的轴向磁通密度轴向分量大小为

(17)

半径为r的分体电枢的径向受力大小为

(18)

通过对电枢模型进行分析与公式推导可得,电枢受力与初级线圈电流、电枢感应电流、磁通密度有关,其中轴向力为电枢向前运动的主要动力,径向力为电枢产生形变的主要原因。

2 有限元仿真分析

在有限元分析模型中,采用容量为4 000 μF、充电电压3 kV的脉冲电容器为电磁同步线圈推进器提供电流,模拟推进器推进时间为3 ms。在模型分析中,忽略电枢与推进器之间的摩擦,不考虑空气阻力对电枢的影响。

2.1 电磁同步线圈推进器性能分析

在推进过程中,脉冲电容器放电产生的电流波形如图7所示,电流随时间呈现出先增后减的变化,在0.45 ms左右为初级线圈电流峰值为26.0 kA。在图7中也给出了电枢轴向受力波形,电枢轴向受力呈先增后减再增的变化,在初级线圈电流峰值时刻电枢轴向受力最大为132.4 kN,在推进过程中,电枢在轴向上不仅受到正向电磁力,随着线圈电流下降过程中,电枢还受到反向力,此反向力会引起电枢做减速运动。

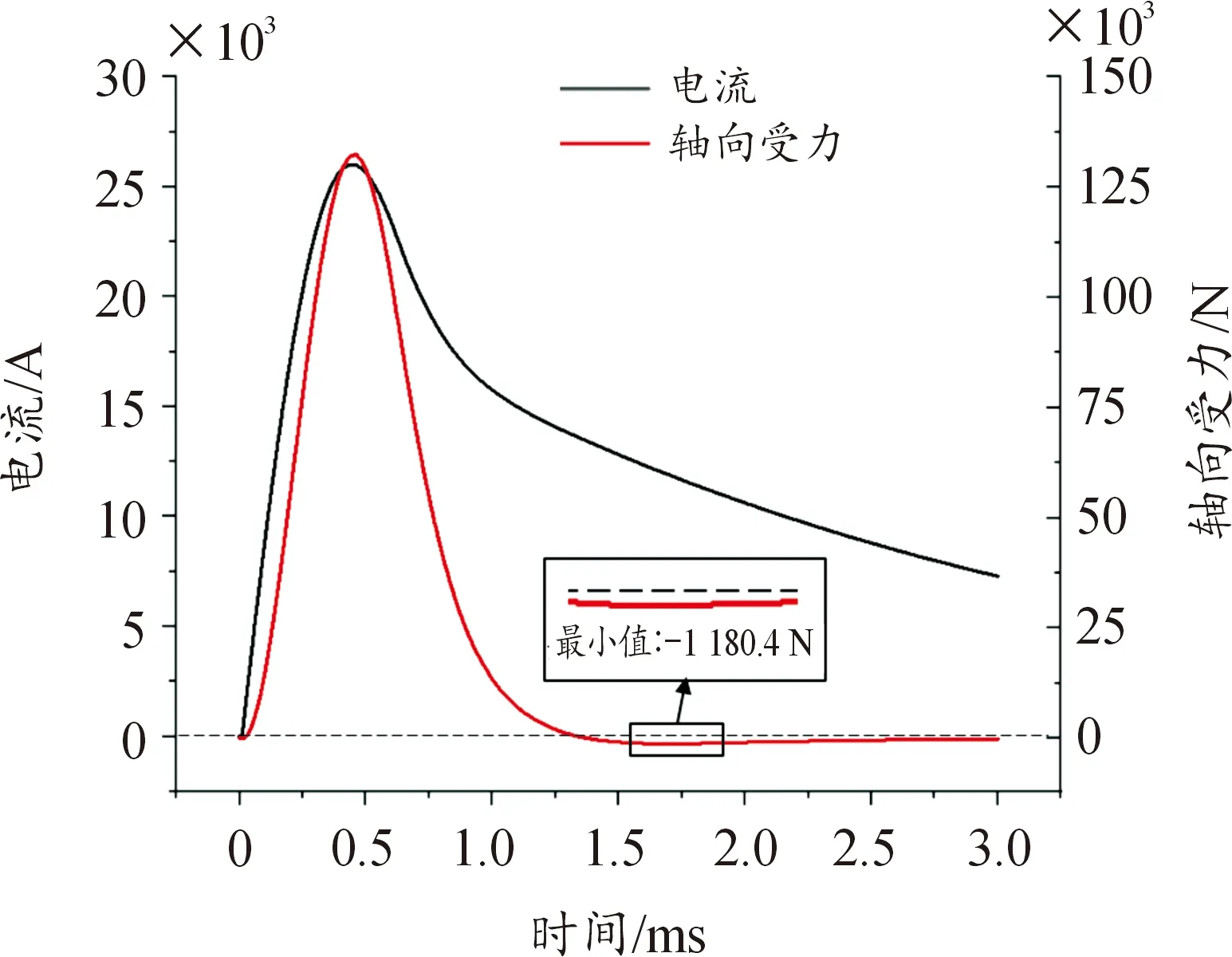
图7 初级线圈电流波形与电枢轴向受力波形

电枢在电磁力的作用下速度呈现出先增后减的变化,最大速度为68.5 m/s,最大位移为171 mm,电枢速度位移波形图如图8所示。

图8 电枢速度与位移波形

2.2 电磁同步线圈推进器磁场仿真分析

在推进过程中,电磁同步线圈推进器各时间段的磁场分布如图9所示,其中红色箭头表示磁场方向。起初磁场主要集中于推进器内的下部和初级线圈附近,且越靠近初级线圈磁场强度越高;在电枢附近,磁场方向发生了明显的改变,磁场没有完全扩散进电枢,而是聚集在电枢与线圈夹缝中,这表示在电枢内部感应出了环状电流,并且该感应电流阻止磁场扩散进电枢。当电枢移动至推进器外后,线圈环内磁场恢复至正常。

2.3 电磁同步线圈推进器电流密度仿真分析

初级线圈由均匀多匝铜线绕制而成,电流密度在线圈中均匀分布;而电枢上感应电流密度则受趋肤效应的约束,主要集中在尾部和外表面,沿电枢尾部至前端方向,感应电流密度呈逐渐降低的趋势。感应电流密度在沿外表面至内表面方向也具有相同变化规律,初级线圈和电枢上电流密度及电流方向分布如图10所示。

初级线圈通入电流为单一方向电流,由零时刻开始通入电流逐渐增大,在电枢附近产生的磁场也逐渐增强。依据楞次定律,为阻止电枢内磁通的变化,电枢中感应出与初级线圈反方向的电流如图10(a)、图10(b)所示。待初级线圈内电流达到峰值后,电流逐渐减小,电枢附近磁场强度和电枢内磁通也逐渐降低,为阻止电枢内磁通的变化,电枢将感应出与初级线圈同向电流,电枢感应正向电流主要集中在电枢的尾部外侧,其他位置为反向电流。电枢感应电流密度分布如图10(c)、图10(d)所示,随着电枢内感应正向电流的范围逐渐扩大,电枢尾部外侧与电枢其他部分感应出明显的分割线,这是由于电枢尾部与电枢其他位置感应电流方向不一致相互抵消导致的。

图9 磁场分布

2.4 电磁同步线圈推进器应力仿真分析

起初电枢感应电流密度方向和初级线圈电流密度方向相反,电枢周围磁场在轴向的分量为向上方向,依据式(2),电枢在径向上受力为沿径向向内,受到挤压力,电枢在0.2 ms和0.45 ms时刻受力分布分别如图11(a)、图11(b)所示,其中红色箭头方向代表受力方向。随着初级线圈电流的减小,电枢尾部感应电流密度方向发生反转,此时周围磁场在轴向的分量方向不变,电枢尾部在径向受到向外的拉力,其他部位在径向上受到向内的压力,在0.8 ms和1.2 ms时刻电枢受力分布分别如图11(c)、图11(d)所示。在推进过程中电枢尾部外侧感应电流密度和磁场强度均为最大值,故电枢尾部外侧受电磁力最大。

初级线圈电流密度为正向,附近磁场在轴向上分量为向上方向,依据式(2),初级线圈在径向方向受到向外的力。初级线圈内侧的磁场强度比外侧磁场强度大得多,因此线圈内侧受电磁力更大,在推进过程中电枢与初级线圈的夹缝为磁场的聚集点,即初级线圈离电枢越近的部位受到的电磁力越大。

2.5 仿真分析小结

通过有限元模型分析可以得出,电枢在运动过程中,电枢的尾部的磁场强度、感应电流密度、应力都是最大值,易导致电枢产生向内形变,因此电枢内部需要增加支撑,线圈整体受向外的应力。此外,由于在电枢运动过程中,电枢尾部对应初级线圈位置受力最大,应适当增加内侧材料厚度,延长推进器使用寿命。

3 电枢形变验证与优化

为验证电磁同步线圈推进器在推进过程中电枢的形变量,搭建了电磁同步线圈推进器实验平台,电枢与初级线圈参数与有限元分析模型保持一致。

在实验过程中,电枢采用铝合金材料。单次实验电枢形变量过于微小,约为0.2 mm,不易测量与观察,故采用多次实验叠加实验效果,在20次同参数实验后,电枢尾部形变量约为3.8 mm,将仿真模型在推进过程中最大形变量放大20倍后,电枢形变量约为3.6 mm,电枢实验后形变量与仿真模型形变量对比如图12所示。仿真模型与实际模型形变位置一致,有限元分析结果与实验结果的形变趋势与形变量保持一致。

电枢所受到的径向电磁力为电枢产生形变的主要原因。由于电流具有趋肤效应,电枢内侧感应电流要小于电枢外侧感应电流。感应电流会阻止磁场向电枢内部扩散,因此,与电枢内部相比,电枢外部的磁场及受力均明显更高,形变量也更显著。以电枢外表面为横向坐标轴,形变量大小为纵向坐标轴进行绘图,不同时刻电枢外表面的形变量如图13所示,在推进过程中,电枢首先向内产生形变,形变量由小到大再减小;随着时间的变化,电枢尾部位置产生向外的形变,其中t=0.45 ms时刻为初级线圈电流的峰值时刻,即电枢受最大电磁力时刻,此时电枢尾部位置的形变量为最大值0.184 mm。

图12 电枢形变图

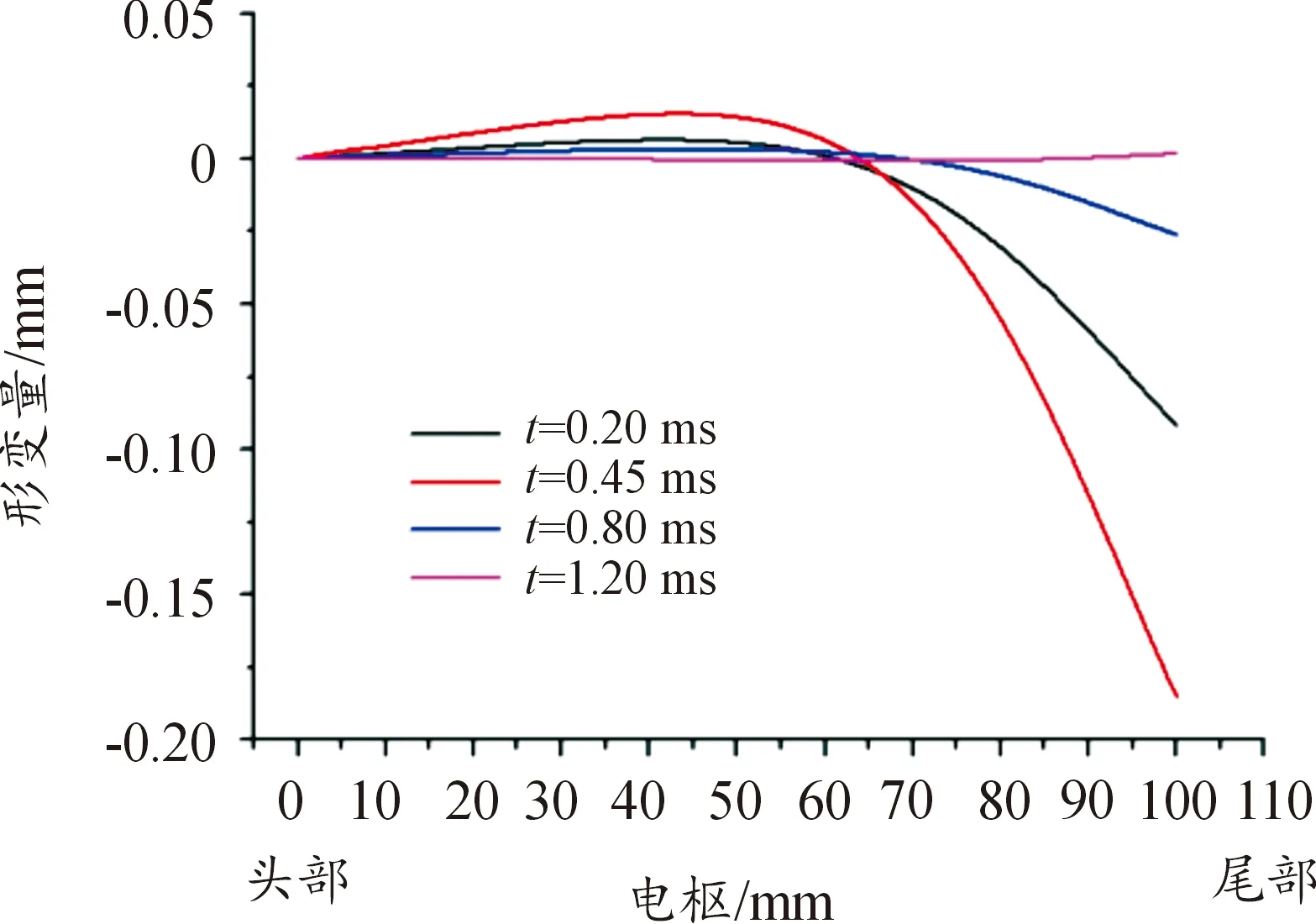
图13 电枢边界形变量

为减小电枢的形变量,对电枢结构进行优化,通过在电枢内部增加与电枢同材料加强筋的方法,来增加电枢在径向上承受电磁力的能力,共设计5种电枢优化方案,优化方案截面图如图14所示。

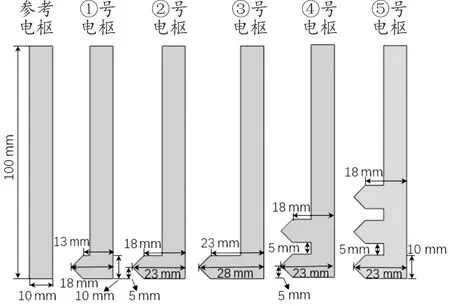
图14 优化方案电枢截面图

为探究不同优化方案电枢的应力与形变效果,对5种优化方案进行了有限元仿真,通过调节配重块质量,保证推进物体质量一致,在电流峰值时刻t=0.45 ms时电枢应力分布如图15所示,其中箭头方向为电枢受力方向,此时电枢外边界形变量分布分别如图16所示。推进器基本性能参数如图17所示。

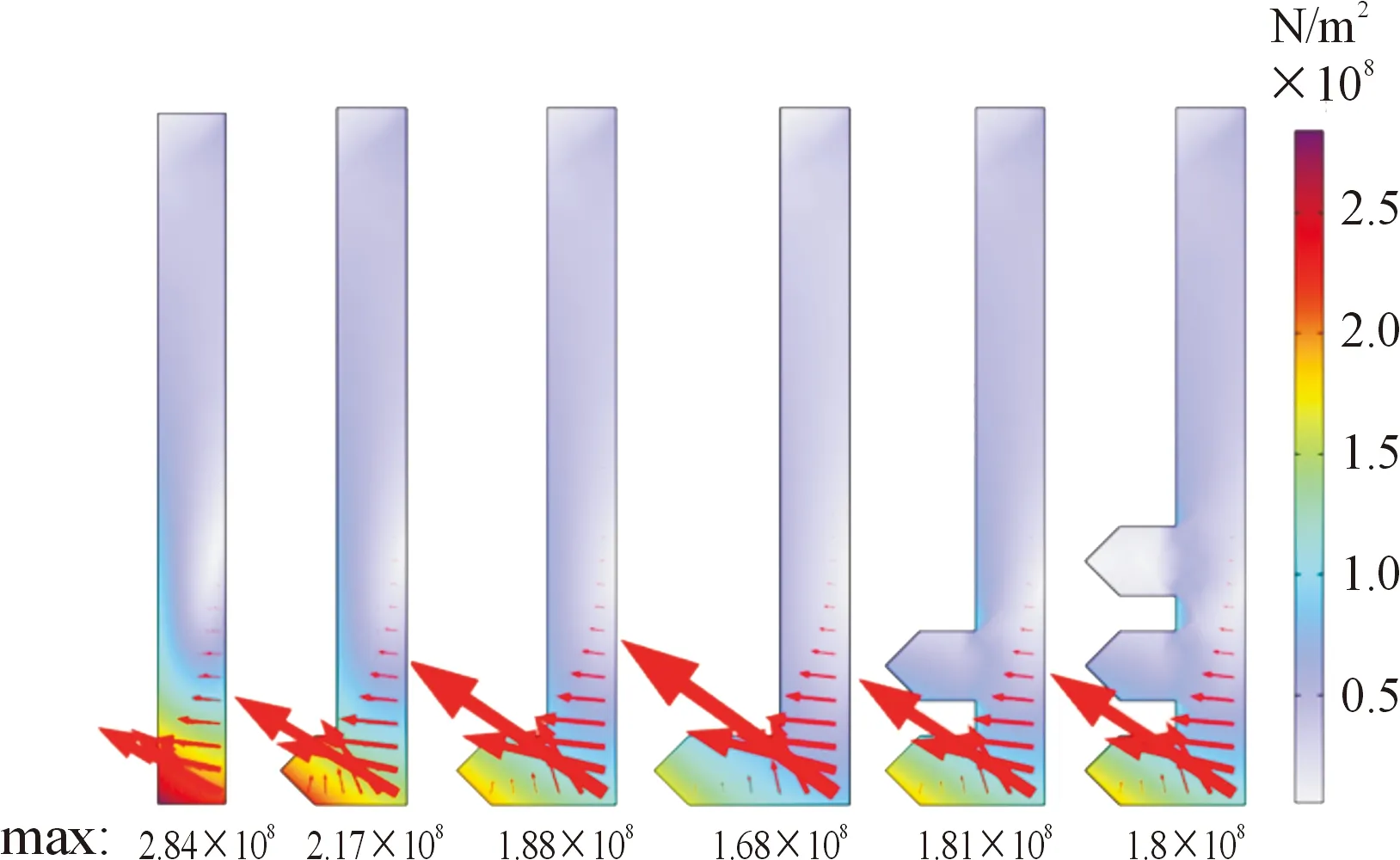
图15 电枢应力分布

图16 外侧边界形变量

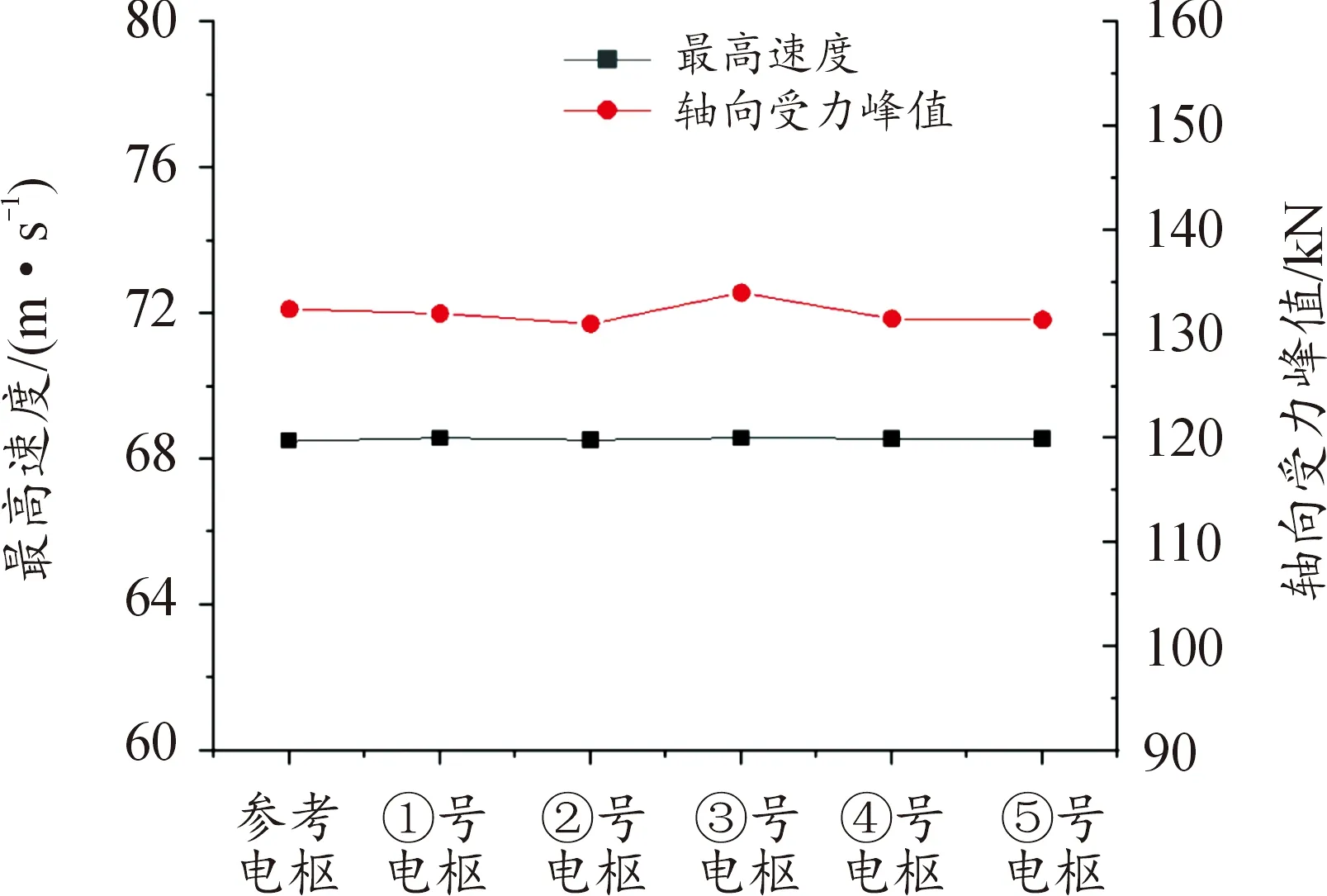
图17 性能参数

其中5种优化电枢方案与参考电枢相比,最高速度与最高轴向受力峰值均未有太大偏差,基本性能保持一致;由①、②、③号电枢方案和参考电枢仿真结果对比可知,增加电枢加强筋长度,最大应力值与最大形变量均逐渐减小;由②、④、⑤号电枢方案与和参考电枢方案仿真结果对比可得,增加加强筋厚度,最大应力值与最大形变量虽然也呈减小趋势,但效果不明显,其中④、⑤号电枢形变分布基本一致。最优结构电枢为③号电枢,最大应力值为1.68×108N/m2,尾部最大形变量仅为0.078 mm,与参考电枢相比,最大应力和最大形变分别减小约40%和57%。

4 结论

针对电磁同步线圈推进器在推进过程中动态力学状态研究,通过理论推导、仿真模拟和试验结果进行分析总结,得出以下结论:

1) 初级线圈的最大受力位置为最内侧线圈,且与电枢距离越近的位置,受应力越大,可以适当增加绝缘固定外壳在线圈内侧的厚度,增加推进器的稳定性。

2) 电枢尾部为受应力值与形变量最大位置,可以通过在电枢尾部增加加强筋,来减小电枢形变。

3) 电枢尾部加强筋长度越长,电枢所受应力与形变量越小,电枢尾部加强筋厚度对电枢应力值与形变量影响较小,本文中最优方案与参考电枢相比最大应力值减小了约40%,尾部最大形变减小了约57%。在重量允许的情况下,应优先对电枢尾部进行拉筋处理。