平面Acrobot和Pendubot的统一控制策略
黄自鑫,侯梦毓,危少奇,王乐君
1)南开大学人工智能学院,天津 300071;2)武汉工程大学电气信息学院,湖北武汉 430205;3)武汉工程大学智能机器人湖北省重点实验室,湖北武汉 430205;4)武汉纺织大学湖北省数字化纺织装备重点实验室,湖北武汉 430200;5)重庆邮电大学自动化学院,重庆 400065
欠驱动机械系统[1-3]是一类控制输入个数少于系统自由度的系统,即系统的部分驱动装置失效或缺失.相对于全驱动系统,欠驱动系统因驱动装置数目减少,可有效降低成本、减轻系统质量[4].欠驱动系统在日常生活中应用广泛,如水面舰船[5]、四旋翼无人机[6]、倒立摆[7]和双足机器人[8]等.欠驱动系统的控制问题是当前非线性控制领域的一个研究热点[9-10].由于欠驱动系统具有强耦合性和非线性[11],使得系统的稳定控制具有很大挑战性.
平面欠驱动机械臂是一类典型的欠驱动系统[12].连杆数目和被动关节位置的变化,令平面欠驱动机械臂的类型呈现多样性.根据被动关节的位置不同,平面两连杆欠驱动机械臂可分为平面Acrobot和平面Pendubot.其中,前者的第1关节和后者的第2关节为欠驱动的.具有角度约束的平面Acrobot 属于完整系统.基于平面Acrobot 控制特性和角度约束关系,LAI等[13]提出一种可同时实现系统驱动连杆和欠驱动连杆控制目标的方法.CAO等[14]根据平面Acrobot 角度约束关系,提出一种基于模糊控制的位置控制方法,实现了系统连杆的控制目标.平面Pendubot具有角加速度约束关系,属于二阶非完整系统.HUANG 等[15]利用该系统的幂零近似特性,设计一种开环迭代控制策略来实现系统连杆的控制目标.WU等[16]提出一种基于傅里叶变换和智能优化的平面Pendubot控制策略.设计了一种时间相关控制器,实现系统连杆从初始位置移动到目标位置的控制目标.
对于平面多连杆欠驱动机械臂,LAI 等[17]以平面PAAA(具有第1被动关节的平面四连杆欠驱动机械臂,P表示被动关节,A表示驱动关节)为研究对象,提出一种基于遗传算法的位姿控制策略,在每个控制阶段将系统简化为平面虚拟Acrobot,通过控制简化后的系统实现控制目标.盛阳等[18]针对平面PAAA系统,提出基于模型降阶的控制方法,利用系统特性控制虚拟的平面Acrobot,从而实现对原系统的位置控制目标.针对平面APA 系统,黄自鑫等[19]将原系统降阶为平面虚拟Acrobot 和平面虚拟Pendubot,通过控制这两个系统,实现对原系统的控制.HUANG 等[20]针对末关节为被动的平面AmP系统,提出一种基于智能优化算法的模型降阶控制策略,通过将系统退化为平面虚拟Pendubot来进行控制.上述平面多连杆欠驱动机械臂的控制策略都是通过将复杂的原系统退化为平面Acrobot 和平面Pendubot 来进行稳定控制.可见,对平面Acrobot和平面Pendubot的控制研究可促进平面多连杆欠驱动机械臂控制方法的发展.
由于被动关节位置的不确定性,若要实现对平面两连杆欠驱动机械臂的有效控制,需探索出一种同时适用于平面Acrobot 和平面Pendubot 的统一控制策略.但是,当平面全驱动机械臂的某一关节发生故障而成为被动关节时,若无法直接确定该被动关节的位置,现存的控制方法将难以直接应用.因此,若要在此情况下实现对平面两连杆欠驱动机械臂的有效控制,必需探索一种适用平面Acrobot 和平面Pendubot的统一控制策略.为解决此问题,本研究以平面Acrobot 和平面Pendubot 为研究对象,提出一种基于轨迹规划和跟踪控制的统一控制策略.首先,建立系统动力学模型并展开分析.然后,将系统控制过程分为两个控制阶段:第1 阶段,在控制器的作用下,驱动连杆沿着预先设计好的轨迹运动,从初始状态运动到目标状态.此时,欠驱动连杆进行自由旋转运动.第2阶段,为实现欠驱动连杆的控制目标,对驱动连杆设计一条振荡轨迹,并借助差分进化算法计算优化后的可调轨迹参数.控制器控制驱动连杆追踪轨迹在目标状态处作振荡运动.当驱动连杆重新稳定在目标状态时,欠驱动连杆也将达到并稳定在目标状态处.最后,利用仿真实验验证所提控制策略的有效性和普适性.
1 系统建模和特性分析
在对平面Acrobot 和平面Pendubot 系统特性进行分析前,先要构建系统对应的物理结构模型.基于已知的系统物理结构模型,建立系统对应的动力学模型(图1).其中,mi为系统第i(i= 1,2)个连杆的质量;Li为第i根连杆的长度;li为第i根连杆的质心到前一关节的长度;Ji为第i根连杆的转动惯量.

图1 平面两连杆欠驱动机械臂结构模型(a)平面Acrobot;(b)平面PendubotFig.1 Structural models of planar 2-link underactuated manipulator for (a) planar Acrobot and (b) planar Pendubot.
根据欧拉-拉格朗日法建立平面Acrobot 和平面Pendubot的统一动力学方程为
其中,M(q)为具有正定性和对称性的惯性矩阵,M(q) =(Mij)2×2;q、q̇和q̈分别为系统关节的角度向量、角速度向量和角加速度向量,q=(qi)2×1,q̇=(q̇i)2×1,q̈=(q̈i)2×1;H(q,q̇)为科式力和离心力的结合矩阵,H(q,q̇) =(Hi)2×1;M(q)和H(q,q̇)具体计算过程可参考文献[14-15];τ为施加在各个关节上的力矩向量(平面Acrobot为τ= [0τ2]T,平面Pendubot为τ= [τ10]T.其中,i= 1,2,分别指第1和第2关节.
设系统状态向量x=[x1x2x3x4]T=[q1q2q̇1q̇2]T,令x的导数为
由式(1)可知,平面Acrobot 和平面Pendubot 欠驱动连杆对应的耦合约束方程为
其中,a和p分别为驱动连杆和欠驱动连杆,对于平面Acrobot 有a=2,p= 1,对于平面Pendubot 有a= 1,p= 2;q̈a和q̈p分别为驱动连杆和欠驱动连杆的角加速度.
由式(3)可得,ts时刻系统欠驱动连杆和驱动连杆对应的运动状态约束关系为
其中,qp0和q̇p0分别为系统欠驱动连杆的初始角度和初始角速度.
2 第1阶段控制
2.1 轨迹规划
在第1阶段的控制过程中,需要实现系统驱动连杆的控制目标.为此,设计驱动连杆相应的运动轨迹为
其中,q͂a=qaf-qa0;qa0为驱动连杆的初始角度;qaf为驱动连杆的目标角度;t1为第1 阶段结束时间,本研究取t1= 1 s..由式(5)可知,当沿着该轨迹运动时,驱动连杆将从其初始位置qa0出发,在t1时刻到达目标状态qaf处,从而实现对系统驱动连杆的控制目标.
2.2 跟踪控制器设计
根据驱动连杆的控制目标,构造李雅普诺夫函数为
其中,μa1=xa-S1(t);P1为PD控制器的控制系数;xa为驱动连杆对应的状态.
对V1(x)关于时间t求导,则由式(2)可得
其中,gaa和fa分别为矩阵M(q)和f(x)中驱动连杆对应参数;τa为施加在驱动连杆上的力矩.
设计第1阶段控制的轨迹跟踪控制器为
其中,D1为PD 控制器的控制系数.由于系统的惯性矩阵M(q)为正定对称矩阵,可得到gaa≠0.
将式(8)带入式(7),可得
可见,若V̇1(x)≤0,则V1(x)有界.定义
其中,C1为正的常数.对于任意x∈Φ1,当t≥0时,x依旧属于Φ1.
设Ψ1为不变集
由式(9)可知,当V̇1(x)= 0 时,可得xa+2= 0.代入式(8),可得
将式(12)代入式(8)可得xa=qad.在此控制阶段,驱动连杆的最大不变集为
根据LaSalle 不变原理,式(10)从Φ1出发的任意x都将收敛于M1,表示为
其中,e1和e2为很小的正数.在t1时刻,式(14)成立.此时,欠驱动连杆的角度和角速度可分别表示为qp(t1)和q̇p(t1).
3 第2阶段控制
3.1 轨迹规划
为实现对系统欠驱动连杆的控制,基于驱动连杆和欠驱动连杆的耦合关系,针对驱动连杆设计一条带有可调参数的振荡轨迹如式(15),再通过控制驱动连杆实现对欠驱动连杆的控制目标.

由式(15)可知,驱动连杆将追踪第2阶段的运动轨迹S2(t)从目标状态出发做振荡运动,并在t ≥tf时返回目标状态.
当t=t1且t ≥tf时,Ṡad2(t) =S̈ad2(t) = 0;
当t1<t <tf时,
其 中 ,φ(x)= 1 - tanh2x,γ(α,β) = tanhα-tanhβ.
一般情况下,当系统驱动连杆稳定在目标状态时,由于缺少对应的控制输入,欠驱动连杆将处于一个不确定的运动状态.为了确保借助所设计的轨迹,可以使得欠驱动连杆在tf时刻稳定在目标状态,即qp(tf) =qpf,q̇p(tf) = 0.下面利用差分进化算法优化可调轨迹参数Am、w和tf从而实现驱动连杆和欠驱动连杆控制目标.
3.2 参数优化
根据欠驱动连杆目标状态设计评价函数为
其中,qp(tf)和q̇p(tf)分别为欠驱动连杆在tf时刻的角度和角速度;qpf为欠驱动连杆的目标角度.
利用差分进化算法优化轨迹参数Am、w和tf的过程概括为:
1)随机生成初始种群,假设轨迹参数Am、w和tf的初始值分别为A͂m、w͂和t͂f.
2)根据式(15)—式(17)、A͂m、w͂和t͂f,分别计算qp(tf)和q̇p(tf)并代入式(18),计算适应度函数h1.
3)当h1≤ε1(ε1为很小的正数)时,可得轨迹参数Am=A͂m,w=w͂,tf=t͂f;否则,执行下一步.
4)经过变异、交叉和选择操作更新A͂m、w͂和,转到2).
基于优化后的轨迹参数A͂m、w͂和t͂f,可得确定的驱动连杆轨迹S2(t).根据S2(t)可设计轨迹跟踪控制器来追踪该轨迹.
3.3 轨迹跟踪控制器设计
构造李雅普诺夫函数为
其中,P2为控制器的控制系数;μa2=xa-S2(t).
对V2(x)关于时间求导,可得
设计轨迹跟踪控制器为
其中,D2为PD 控制器的控制系数.将式(21)代入式(20),可得
由V̇2(x)≤0可知,V2(x)有界.定义
其中,C2为正数.对于属于Φ2的任意x,当t≥0时,x仍属于Φ2.设不变集为
由式(22)可知,当V̇2(x)= 0 时,xa+2= 0.将xa+2= 0代入式(2),可得
将式(25)代入式(21),可得xa=qaf.因此,在此控制阶段,驱动连杆的最大不变集可表述为
根据LaSalle 不变原理,当t→∞,从Ψ2出发的任意x都将收敛于M2.
4 系统仿真
以平面Acrobot 和平面Pendubot 为控制对象进行Matlab/Simulink 仿真实验.针对平面Acrobot 和平面Pendubot,分别选取两组不同的实验参数进行仿真实验,以验证所提控制策略的有效性和普适性.
平面Acrobot 和平面Pendubot 的模型参数选取如表1.控制器(9)和(21)参数设置为:P1=P2= 1和D1=D2= 1.8;差分进化算法参数设置为:变异因子pm= 0.3,pc= 0.7,迭代次数Gmax= 200,评价函数的误差范围ε1= 1 × 10-4,t1=tr=td= 1 s.

表1 平面两连杆欠驱动机械臂模型参数Table 1 Model parameters of the planar two-link underactuated manipulator.
4.1 仿真1
为验证所提控制策略的可行性,选取一组参数搭建系统Simulink 模型,利用Matlab 软件进行第1组可行性验证仿真.平面Acrobot 和平面Pendubot系统两个连杆的初始状态(角度和角速度)和目标状态参数分别设置为[q10q20q1dq2d]= [0 0 -0.847 6.481]rad和[q̇10q̇20q̇1dq̇2d] = [0 0 0 0]rad/s.
采用智能优化算法求得优化后的轨迹参数,平面Acrobot 为A1= 0.22 rad、w= 2.76 rad/s 和tf=2.23 s;平面Pendubot 为A2= 0.90 rad、w= 0.56 rad/s和tf= 3.42 s.
平面Acrobot的第1组仿真结果如图2所示.由图2 可知,当t= 2.23 s 时,平面Acrobot 系统驱动连杆和欠驱动连杆的角度和角速度最终都将稳定在其目标状态处,实现了系统的控制目标,且在整个控制过程中,系统控制输入的力矩始终维持在[-20 20]N·m.

图2 平面Acrobot的(a)角度、(b)角速度和(c)力矩的第一组仿真结果Fig.2 (Color online) The first simulation results of (a) angle, (b) angular velocity, and (c) torque for planar Acrobot.
平面Pendubot 第1 组仿真结果如图3 所示.当t= 3.42 s时,系统驱动连杆和欠驱动连杆的角度和角速度都将从初始值逐渐到达目标值,成功实现系统的稳定控制目标.并且在此控制过程中,系统的控制输入力矩在[-25 20]N·m.

图3 平面Pendubot的(a)角度、(b)角速度和(c)力矩的第一组仿真结果Fig.3 (Color online) The first simulation results of (a) angle, (b) angular velocity, and (c) torque for planar Pendubot.
4.2 仿真2
为进一步验证所提控制策略的普适性,需选取与第1 组仿真不同的实验参数进行普适性验证仿真,系统驱动连杆和欠驱动连杆的初始角度、角速度和目标角度、角速度参数选为[q10q20q1d q2d]= [0 0 -0.517 2.419]rad 和[q̇10q̇20q̇1dq̇2d] =[0 0 0 0]rad/s.
采用差分进化算法求得优化后的轨迹参数,平面Acrobot 为A1= 0.07 rad,w= 1.76 rad/s,tf=4.55 s;平面Pendubot 为A2= 0.26 rad,w= 3.42 rad/s,tf= 3.72 s.
平面Acrobot 第2 组仿真结果如图4.由图4 可见,当t= 4.55 s 时,平面Acrobot 其驱动连杆和欠驱动连杆的角度、角速度最终都将稳定在其目标值处,系统的控制目标实现.

图4 平面Acrobot的(a)角度、(b)角速度和(c)力矩的第二组仿真结果Fig.4 (Color online) The second simulation results of (a) angle, (b) angular velocity, and (c) torque for planar Acrobot.
平面Pendubot 第2 组仿真结果如图5 所示,当t= 3.72 s 时,系统驱动连杆、欠驱动连杆的角度、角速度将从初始值逐渐到达其目标值,成功实现系统的控制目标.

图5 平面Pendubot的(a)角度、(b)角速度和(c)力矩的第二组仿真结果Fig.5 (Color online) The second simulation results of (a) angle, (b) angular velocity, and (c) torque for planar Pendubot.
4.3 仿真3
考虑到实际情况中存在的干扰因素对系统控制的影响,选取与第1组仿真相同的初始状态和目标状态进行第3组加入干扰因素的仿真实验,在仿真进行全程中加入一个值为0.01的干扰常数.
通过差分进化算法求得优化后的轨迹参数,平面Acrobot 为A1= -0.72 rad,w= -0.88 rad/s,tf=4.67 s;平面Pendubot 为A2= 3.65 rad,w= 0.13 rad/s,tf= 3.35 s.平面Acrobot 第3 组仿真结果如图6所示.平面Pendubot第3组仿真实验结果如图7所示.

图6 干扰影响下平面Acrobot的(a)角度、(b)角速度和(c)力矩仿真结果Fig.6 (Color online) Simulation results of (a) angle, (b) angular velocity, and (c) torque for planar Acrobot with interference.

图7 干扰影响下平面Pendubot的(a)角度、(b)角速度和(c)力矩仿真结果Fig.7 (Color online) Simulation results of (a) angle, (b) angular velocity, and (c) torque for planar Pendubot with interference.
由图6 和图7 可知,当仿真中加入1 个干扰因素后,在t= 4.67 s 和t= 3.35 s 时,本研究所提控制策略分别实现了对平面Acrobot 和Pendubot 的控制目标,证明在干扰因素存在的前提下,所提控制策略对具有不同特性和结构的平面两连杆欠驱动机械臂控制具有普适性.
4.4 仿真4
为验证所提控制策略的先进性,选取与文献[13,15]中相同的参数来进行第4组对比仿真实验.
以平面Acrobot 为控制对象,将本研究所提控制策略与文献[13]所提控制方法进行对比.仿真中,系统初始状态和目标状态选取与文献[13]相同数值,即[q10q20q1fq2f]=[0 0 -1.999 14.106]rad和[q̇10q̇20q̇1fq̇2f] = [0 0 0 0]rad/s.
通过差分进化算法求得优化后的轨迹参数为A1= -3.38 rad,w= 4.52 rad/s,tf= 3.21 s.平面Acrobot 第4 组对比仿真结果如图8 所示.由图8 可知,所提控制策略在t= 3.21 s 时实现了平面Acrobot的控制目标.与文献[13]中的控制方法在t= 6 s实现控制目标相比,本研究控制策略实现控制目标所用时间更短,更具先进性.

图8 对照仿真中,平面Acrobot的(a)角度、(b)角速度和(c)力矩仿真结果Fig.8 (Color online) The results of (a) angle, (b) angular velocity, and (c) torque for planar Acrobot in comparative simulation.
以平面Pendubot为控制对象,将本研究所提控制策略与文献[15]中的控制策略进行对比,系统的初始状态和目标状态选取与文献[15]相同数值,即[q10q20q1fq2f]= [2.80 1.90 2.01 0.94]rad 和[q̇10q̇20q̇1fq̇2f]= [0 0 0 0]rad/s.
通过差分进化算法求得优化后的轨迹参数为A1= 1.04 rad,w=1.14 rad/s,tf= 6.62 s.平面Pendubot第4组对比仿真结果如图9所示.由图9可见,当t= 6.62 s 时,平面Pendubot 连杆角度和速度都到达了目标值.与文献[15]所提控制策略在t=65.29 s 时实现平面Pendubot 的控制目标相比,本研究所提控制策略实现控制目标所用时间更短,具有一定的先进性.
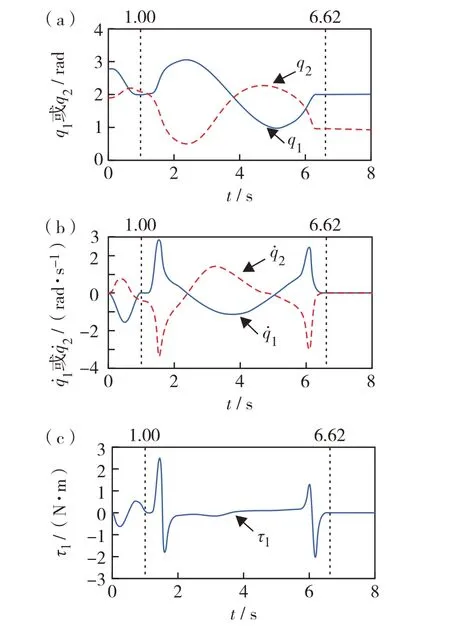
图9 对照仿真中,平面Pendubot的(a)角度、(b)角速度和(c)力矩结果Fig.9 (Color online) The results of (a) angle, (b) angular velocity, and (c) torque for planar Pendubot in comparative simulation.
结 语
针对平面两连杆欠驱动机械臂的统一控制问题展开研究,提出一种基于轨迹规划和跟踪控制的控制策略.在两个控制阶段规划轨迹并追踪轨迹运动,成功实现了系统驱动连杆和欠驱动连杆的控制目标.采用差分进化算法实现轨迹参数的优化,使对平面Acrobot 和平面Pendubot 的控制更加稳定.未来还将开展对被动关节处于不同位置的平面多连杆欠驱动机械臂统一控制问题展开研究,以期提高平面多连杆欠驱动机械臂的控制效率,进一步推动平面欠驱动机械臂和非线性系统控制理论的发展.
参考文献 / References:
[1]HUANG Zixin, WEI Shaoqi, HOU Mengyu, et al.Finitetime control strategy for swarm planar underactuated robots via motion planning and intelligent algorithm [J/OL].Measurement and Control.(2022-09-20).doi:10.1177/00202940221116606..
[2]黄自鑫,秦翔宇,陈振,等.基于智能优化算法的欠驱动机械臂位姿控制[J].控制工程,2022,29(11):1948-1953.HUANG Zixin, QIN Xiangyu, CHEN Zhen, et al.Positionposture control of planar underactuated manipulator based on intelligent optimization algorithm [J].Control Engineering of China, 2022, 29(11): 1948-1953.(in Chinese)
[3]黄自鑫,王乐君.一类平面欠驱动机械系统控制方法综述[J].武汉工程大学学报,2021,43(4):448-454,467.HUANG Zixin, WANG Lejun.Review of control method of planar underactuated mechanical system [J].Journal of Wuhan Institute of Technology, 2021, 43(4): 448-454,467.(in Chinese)
[4]ZHANG Ancai, SHE Jinhua, QIU Jianlong, et al.Design of motion trajectory and tracking control for underactuated cart-pendulum system [J].International Journal of Robust and Nonlinear Control, 2019, 29(8): 2458-2470.
[5]刘壮.欠驱动水面舰船航迹自抗扰系统的研究与设计[J].舰船科学技术,2017,39(14):31-33.LIU Zhuang.Research and design of auto-disturbance rejection system for underactuated surface ship [J].Ship Science and Technology, 2017, 39(14): 31-33.(in Chinese)
[6]刘子龙,窦鹏程.四旋翼无人机的位置和姿态控制算法研究[J].小型微型计算机系统,2022,43(4):754-758.LIU Zilong, DOU Pengcheng.Position and attitude control algorithm study of quadrotor UAV [J].Journal of Chinese Computer Systems, 2022, 43(4): 754-758.(in Chinese)
[7]HUANG Zixin, LAI Xuzhi, ZHANG Pan, et al.A general control strategy for planar 3-DoF underactuated manipulators with one passive joint [J].Information Sciences, 2020,534: 139-153.
[8]王雨轩,陈思溢,黄辉先.基于改进深度强化学习的倒立摆控制器设计[J].控制工程,2022,29(11):2018-2026.WANG Yuxuan, CHEN Siyi, HUANG Huixian.Inverted pendulum controller based on improved deep reinforcement learning [J].Control Engineering of China, 2022, 29(11): 2018-2026.(in Chinese)
[9]韩连强,陈学超,余张国,等.面向离散地形的欠驱动双足机器人平衡控制方法[J].自动化学报,2022,48(9):2164-2174.HAN Lianqiang, CHEN Xuechao, YU Zhangguo, et al.Balance control of underactuated biped robot for discrete terrain [J].Acta Automatica Sinica, 2022, 48(9): 2164-2174.(in Chinese)
[10]张春蕾,王立东,高闯,等.输入饱和及输出受限的纯反馈非线性系统控制[J].控制工程,2021,28(3):531-539.ZHANG Chunlei, WANG Lidong, GAO Chuang, et al.Pure feedback nonlinear system control with input saturation and output constraints [J].Control Engineering of China, 2021, 28(3): 531-539.(in Chinese)
[11]张桐松,邵雪卷,张井岗,等.欠驱动桥式吊车系统的非线性扩张状态观测器设计[J].自动化仪表,2022,43(1):19-28.ZHANG Tongsong, SHAO Xuejuan, ZHANG Jinggang, et al.Design of nonlinear extended state observer for underdrive overhead crane system [J].Process Automation Instrumentation, 2022, 43(1): 19-28.(in Chinese)
[12]HUANG Zixin, LAI Xuzhi, ZHANG Pan, et al.A general control strategy for planar 3-DoF underactuated manipulators with one passive joint [J].Information Sciences, 2020,534: 139-153.
[13]TAFRISHI S A, SVININ M, YAMAMOTO M.Inverse dynamics of underactuated planar manipulators without inertial coupling singularities [J].Multibody System Dynamic,2021, 52: 407-429.
[14]LAI Xuzhi, SHE Jinhua, CAO Weihua, et al.Stabilization of underactuated planar Acrobot based on motion-state constraints [J].International Journal of Non-Linear Mechanics, 2015, 77: 342-347.
[15]CAO Junqing, LAI Xuzhi, WU Min.Position control method fora planar Acrobot based on fuzzy control [C]//The 34th Chinese Control Conference.Piscataway, USA:IEEE, 2015: 923-927.
[16]HUANG Zixin, LAI Xuzhi.Control strategy based on iterative method for planar pendubot [C] // The 37th Chinese Control Conference.Piscataway, USA: IEEE,2018: 858-861.
[17]WU Jundong, WANG Yawu, YE Wenjun, et al.Control strategy based on Fourier transformation and intelligent optimization for planar Pendubot [J].Information Sciences, 2019, 491: 279-288.
[18]LAI Xuzhi, ZHANG Pan, WANG Yawu, et al.Positionposture control of a planar four-link underactuated manipulator based on genetic algorithm [J].IEEE Transactions on Industrial Electronics, 2017, 64(6): 4781-4791.
[19]盛洋,赖旭芝,吴敏.基于模型降阶的平面三连杆欠驱动机械系统位置控制[J].自动化学报,2014,40(7):1303-1310.SHENG Yang, LAI Xuzhi, WU Min.Position control of a planar three-link underactuated mechanical system based on model reduction [J].Acta Automatica Sinica, 2014, 40(7): 1303-1310.(in Chinese)
[20]黄自鑫,秦翔宇,王乐君.二阶非完整平面欠驱动机械系统的位置控制[J].武汉工程大学学报,2021,43(5):567-572.HUANG Zixin, QIN Xiangyu, WANG Lejun.Position control of second-order nonholonomic planar underactuated mechanical system [J].Journal of Wuhan Institute of Technology, 2021, 43(5): 567-572.(in Chinese)
[21]HUANG Zixin, QIN Xiangyu, WANG Lejun, et al.A general control strategy of planar multi-link underactuated manipulator with passive last joint based on nilpotent approximation and intelligent optimization [C]// Chinese Automation Congress.Piscataway, USA: IEEE, 2020:4029-4031.

