曲线导轨上高速磁浮列车运动稳定性

余志武 黎燕霞 徐磊 马建 赵淼

摘要：研究了高速磁浮列車在定常气动荷载作用下曲线上的运动稳定性。建立了考虑气动荷载影响的高速磁浮车在曲线导轨上的动力学模型，经过特征值分析提出了磁浮车的临界速度概念，分析了临界状态时车速、控制参数、气动系数对高速磁浮车曲线导轨上的临界速度影响。结果表明：当系统达到临界状态时，它有两个临界速度。在临界状态条件，位移控制参数由20 000 kN/m降为2 000 kN/m，气动系数从0.05降为0.01，第一类临界速度变大。第一个临界速度出现特征值的实部为零而虚部不为零，第二个临界速度出现在特征值的实部和虚部都为零。失稳是由于偏离平衡位置引起的，位置由曲线导轨特征和侧风荷载产生。气动升力和向心的风荷载会提高稳定性;气动降力和离心的风荷载会降低稳定性;水平角可与向心力配合，竖直角允许设置的范围小。

关键词：高速磁浮列车;临界速度;特征值;气动效应;运动稳定性

中图分类号：U237 文献标志码：A

本文引用格式：余志武，黎燕霞，徐磊，等. 曲线导轨上高速磁浮列车运动稳定性[J]. 华东交通大学学报，2023，40（1）：25-33.

Motion Stability of High-Speed Maglev Train on Curved Track

Yu Zhiwu1，2，Li Yanxia1，2，Xu Lei1，2，Ma Jian3，Zhao Miao3

（1. School of Civil Engineering， Central South University， Changsha 410075， China; 2. National Engineering Research Center of

High-speed Railway Construction， Central South University， Changsha 410075， China; 3. Guangzhou Sifang Bond Industrial Co.，Ltd.， Guangzhou 510700， China）

Abstract：Motion stability of the high-speed maglev vehicle under steady aerodynamic load was studied. The dynamic model of the high-speed maglev vehicle on the curved guideway considering influence of aerodynamic loads was established. The critical speed concept of the maglev vehicle considering aerodynamic loads′ effect based on eigenvalues was presented. Vehicle speed， control parameters， and aerodynamic coefficients to make the critical speed of the high-speed maglev vehicle change in the critical state were also analyzed. The results show that when the system reaches the critical state， it has two critical speeds. Under the conditions in the critical state， the position control parameters vary from 20 000 kN/m to 2 000 kN/m， and aerodynamic coefficients vary from 0.05 to 0.01， the critical speed gets larger. When the real part of the eigenvalue is zero， but the imaginary part is not zero， the first kind of critical velocity occurs. When both the real part and the imaginary part of the eigenvalue is zero， the second kind of critical velocity appears. Instability is caused by the change from the equilibrium position for the curved guideway and wind loads. Aerodynamic downward force and centrifugal wind loads are not good for stability， but aerodynamic upward force and centripetal wind loads improve stability. The horizontal angle can be matched with the centripetal force， but the vertical angle is allowed to be set in a small range.

Key words： the high-speed maglev vehicle; critical speed; eigenvalue; aerodynamic effect; motion stability

磁浮EMS（electric magnetic suspension）车辆具备低能耗、更环保、低噪音、少维护、更强的爬坡能力，更小的曲线半径，受到越来越多的关注。考虑气动荷载，维持磁浮系统在曲线上的运动稳定性对保证磁浮交通的安全至关重要。

一些学者研究了悬浮系统的稳定性。吴晗等[1]计算了车辆导轨耦合系统在考虑间隙反馈控制时滞的影响;黎松奇等[2]推导系统动力稳定应满足的基本条件;洪远卓等[3]利用SIMPACK动力学软件对四模块空簧中置型磁浮车辆的运行稳定性进行了仿真分析;杨志安等[4]应用MLP法得到了磁浮列车响应曲线和相图;洪华杰等[5]得出了防滚装置参数设定的基本准则;梁潇等[6]得到状态观测器参数对系统性能的影响规律;黎松奇等[7]研究磁浮车通过轨道变坡点时稳定性的影响;洪华杰等[8]基于奈奎斯特稳定性理论得到了车轨耦合系统稳定的充分条件;朴明伟等[9]并应用灵敏度函数和最大奇异值进行了鲁棒稳定性分析;马铁刚[10]利用ADAMS和MATLAB协同平台，进行了单轨正交模型的高速运行仿真;陈晓昊等[11]通过Routh-Hurwitz稳定性判据判断系统特征根分布，定量给出了系统发生Hopf分岔时滞临界值;周又和等[12]采用Liapunov特征指数判别动力稳定性;忽伟[13]建立了刚性、柔性轨道的磁悬浮系统模型，得到了控制参数的稳定域。

一些学者研究磁浮车的平面曲线、竖曲线的匹配关系。谢毅等[14]认为线路横坡角小于10°时，平面缓和曲线最小长度主要受最大侧向冲击控制，横坡角继续增大后，则取决于最大横坡扭转率;李茂春等[15]通过作图法对四悬架进行理论计算分析;王泽汉等[16]研究表明目前的车辆参数及结构状态下车辆不可以通过S形曲线;李东帅等[17]研究表明，深度神经网络预测的轨道不平顺值与真实值相对精度超过 99%;时瑾等[18]研究车辆过圆曲线时悬浮力变化，分析转向架结构和圆曲线的几何匹配关系，计算车辆部件偏移量、悬浮力变化量、弹簧变形量等，给出最小圆曲线半径的合理取值;黄志辉等[19]探讨了空气弹簧的最大拉伸量和最大压缩量，计算了第1、第5模块相对车厢的最大点头角;米隆等[20]对平、竖缓和曲线长度及参数匹配关系进行了量化研究;张耿等[21]基于磁通管法得到的电磁力更接近有限元计算结果;代一帆等[22]研究结果表明，相比与凸竖曲线圆曲线半径重叠，凹竖曲线与圆曲线半径重叠具有更好的匹配灵活性。

一些学者关注气动荷载对磁浮车振动的影响。李人宪等[23]研究在横向风的作用下，轮轨型列车的横向稳定性优于磁浮列车，而吸力型的横向稳定性又优于斥力型车;Wu等[24]研究了空气动力效应对高速磁悬浮列车运动稳定性内在机理;Kwon等[25]研究了阵风对磁悬浮列车的响应影响;Yau[26]计算了非定常气流对车辆-轨道耦合系统的影响;武建军等[27]利用有限元软件，采用Kutta-Merson进行动力分析，研究磁悬浮车辆在风场作用下的响应。以上研究对气动荷载计算有了初步的研究，但是没有分析气动荷載对曲线导轨上的磁浮车运动稳定性的影响。下面的几点值得关注：① 在以往的研究中，气动荷载采用有限元方法计算气动力作用在磁浮车辆上，然而气动力是一种随机荷载;② 前面的研究集中在低、中速车辆，气动荷载考虑不多;③ 目前，曲线上的稳定性研究不多。基于前面的考虑，建立一个考虑气动力的双自由度磁浮车模型。使用这个模型，我们可以分析气动荷载对磁浮车运动稳定性的影响。

1 系统模型

刚体横向、竖向两自由度的模型，是分析磁浮车曲线运动的基本单元。如果是考虑磁浮车曲线运动的振动特征，需要考虑多个自由度。但是，分析磁浮车在曲线上的运动宜考虑包含基本运动特征的两个自由度模型。

1） 悬浮器的控制模型。在保证基本精度的前提下，可以对电磁力进行简化。磁流关系在理想平衡点附近线性化。等效磁动刚度和等效磁动阻尼是常量。电磁力的公式如下

FEi=FE0+kep（δ-δ0）+kedδ

FE0

=

kep=

+

ked=a3kd

a1=

（kpδ0-i0R）

a2=

（kpδ0-i0R）2

a3=

（1）

式中：FEi为电磁力，N;FE0为初始电磁力，N;kep为等效磁动刚度，N/m;ked为等效磁动阻尼，N/（m/s）;μ0为真空磁导率;N为电磁铁或圆匝数;Am为有效磁板面积;i0为电流，A;δ为磁铁和桥梁间的间隙;R为电阻。

2） 随机激励模型。ξ1为导轨竖向轨道不平顺激励，ξ2为磁浮车重量横向激励，ξ3为导轨横向轨道不平顺激励，ξ4为磁浮车重量竖向激励。需满足以下关系

Rx1（τ）=E[ξ1（t） ξ1（t+τ）]=2πS1 δ（τ）

Rx2（τ）=E[ξ2（t） ξ2（t+τ）]=2πS2 δ（τ）

Rx3（τ）=E[ξ3（t） ξ3（t+τ）]=2D3 δ（τ）

Rx4（τ）=E[ξ4（t） ξ4（t+τ）]=2D4 δ（τ）  （2）

式中：E为协方差;t为时间变量;τ为时间间隔;S1和S2皆为导轨随机不平顺功率谱密度;D3和D4皆为磁浮车质量激励的白噪声强度。

3） 刚体运动模型。在曲线地段，横坡和纵坡同时存在。所以，刚体的运动平面需通过XOY平面绕Y轴旋转β角度后再绕x轴旋转α角，得xoy平面（图1）。

本文以凸竖曲线进行分析参考。在平、竖曲线重叠地段，列车受到由平曲线产生的水平离心力FH和由竖曲线产生的竖向离心力FV，轨道对列车的支承磁浮力为N，列车受到重力mc的作用，如图1所示。设列车运行速度为v，纵坡坡度为β，平面曲线半径为RH，竖曲线半径为RV[22]。

mcc+sinα+cosα-

（mcgcosβsinα+fhv）-（fmh0-kep1（y-y0）+

ked1y）+kδyξ1（t）+kmc1yξ3（t）=0

mcc+cosα+sinα+

mcgcosαcosβ-fvv-（fmv0-kep2（z-z0）+

ked2z）+kδzξ2（t）+kmc2zξ4（t）=0  （3）

其中，电流和气动力如下：

fmvo=;

fmho=;

I0=（mccosα+mcsinα-

mcgsinαcosβ-fhv/μ0Am）（1/2）

或

I0=（-mccosα+mc

sinα-mcgcosαcosβ-fvv/μ0Am）（1/2）;

kep1=-，

ked1=，

kep2=-，

ked2=。

對于凸竖曲线，竖曲线半径RV取正;对于凹竖曲线，竖曲线半径RV取负;对于竖向气动升力fvv为负，对于竖向气动降力fvv为负;对于横向气动向心力fhv为正，对于横向气动离心力fhv为负;法向vc向下取正，横向zc向右取正;v为速度，m/s;mc为磁浮车质量，kg;fmh0为初始横向磁浮力，N;fmv0为初始竖向磁浮力，N;kep1为磁铁横动刚度，N/m;kep2为磁铁竖向向动刚度，N/m;ked1为磁铁横向动阻尼，N/（m/s）;ked2为磁铁竖向动阻尼，N/（m/s）;y0为磁铁横向初始位移;z0为磁铁竖向初始位移;kδy为导轨横向不平顺系数，kδz为导轨竖向不平顺系数;kmc1为磁浮车重量横向激励系数，kmc2为磁浮车重量竖向激励;kp为PD控制器间隙的反馈系数，kd为PD控制器间隙的一阶导数的反馈系数;u0为电磁铁电压;I0为平衡电流。

fhv=

C2 ρAv（U+v）

fvv=

C3 ρAv（U+v）（4）

式中：ρ为空气密度;Av为车辆的参考面积;C2为横向气动荷载系数;C3为竖向气动荷载系数。

2 力学分析

考虑反馈控制量x=[  y    z]作为状态变量，磁浮车横竖向的系统方程为

=Ax+B  （5）

A=a11 a12 a13 a14

a21 a22 a23 a24

a31 a32 a33 a34

a41 a42 a43 a44，B=b11

b21

b31

b41  （6）

式中：

a11=±ked1，a12=-（kep1+kmc3ξ3（t）），a13=0，

a14=0，a21=1，a22=0，a23=0，a24=0，

a31=0，a32=0，a33=-ked2，

a34=-（kep2+kmc4ξ3（t）），a41=0，a42=0，

a43=1，a44=0;

b11=sinα+cosα-

mcgcosβsinα-fhv/fmh0+kep1y0+kδyξ1（t），

b31=cosα+sinα+

mcgcosαsinβ-fvv/fmv0+kep2z0+kδzξ2（t），

b21=0，b41=0

特征值公式为

λ4 +a1λ3+a2λ2=0 （7）

其中：

a1=ked1+ked2，a2=ked1·ked2

式（5）稳定性的条件为特征根的实数部分小于零。根据劳斯判据准则，非负特征根的充要条件为

a1>0，a1a2>0  （8）

控制参数的范围主要由式（7）确定。如果气动力改变，控制参数的范围也跟着改变。

·>0

或

+>0   （9）

如果反馈控制参数kp固定，电磁铁悬浮间隙y0 与z0 保持不变。根据式（1），当气动力变化，平衡电流I0跟着变化，从而改变了系统的平衡位置。线性化系统式（1）依赖于平衡点的位置（u0，y0）和（u0，z0）。平衡位置的改变影响着闭环系统的特征值矩阵，也影响着式（7）特征值的系数。向心力时稳定，离心力依据条件稳定;升力时稳定，降力依据条件稳定。因此，气动力影响着悬浮系统的稳定性。

随着速度的增加，气动力也增加。自然，平衡点的位置（I0，y0）和（I0，z0）随着速度也变化。这意味着如果不考虑气动力，刚性导轨上的磁浮车系统是独立的。如果考虑气动力，悬浮系统的稳定性与车辆速度息息相关。如果气动力不考虑或者设置为零，控制参数的选择条件满足式（8）。然而，随着速度的增加，气动力超过某一个数值，控制参数就不能满足稳定的条件。因此，磁浮车系统的分叉和失稳就发生了。

依据前面的分析，新的临界速度概念被提出来，用来分析当气动力作用时磁浮车的稳定性。在某一个气动力条件下，当车辆的速度超过一个特定值时，特征矩阵的特征值实数部分等于零，悬浮系统达到了一个临界的状态，分叉产生。这个速度叫作临界速度。

式（5）稳定的充要条件就是特征值的实数部分小于零。在临界状态，特征值的实数部分等于零。假设负数根为λ=α+iβ都是特征方程式（7）的根（α和β都是实数）。将其代入特征方程式，实数部分和虚数部分分离，得到

-α1 β2=0

-β3+α2 β=0（10）

当特征值λ的实数部分等于零，磁浮系统在平衡位置的稳定为临界状态。特征方程的4个特征根包含一对共轭负数根和两个实数根。系统的稳定性有以下两类临界状态。

1） 第一类临界状态：共轭特征根的实数部分为零。因此，α=0，λ=± β，悬浮系统的一个动力分叉（Hopf分叉）发生。这直接导致磁浮系统在干扰作用下出现极限环运动而不是收敛到零。

然后，获得

α1=0，α2= β2  （11）

这种情况导出临界速度vcritical-A。

2） 第二类临界状态：实数特征值等于零。比如，α=β=0，λ=0。因此，一个静态的分叉发生了，导致磁浮车以意外的方式移动和系统的不稳定。因此式（9）变为α2=0。这种情況导出的临界速度vcritical-B和vcritical-B。

3 数值分析

为了分析悬浮系统的稳定性，使用磁浮系统的参数如表1，气动系数如表2。参考铁路设施的空气动力学部分标准（BS EN 14067-6：2018），并计算了气动力。目前，基本没有什么气动力数据。在这次研究中，磁浮车气动力的计算通过使用在高速车-轨耦合的气动分析的相关数据。设置相关的面积为Am=10 m2，空气密度为ρ=1.225 kg/m3，假定风速为10.7 m/s。气动力分为气动升力、气动降力、气动向心力、气动离心力。气动系数不随着车速发生变化。

反馈控制参数设置为kp=20 000，kp=2 000两种工况。选定的反馈控制参数满足不考虑气动力的稳定条件。特征值，考虑车速、气动升力、气动降力、气动离心力、气动向心力，在参数影响下确定了临界速度。

3.1 气动向心力和气动升力

图2和图3分别展示了特征值随着气动力系数的变化。

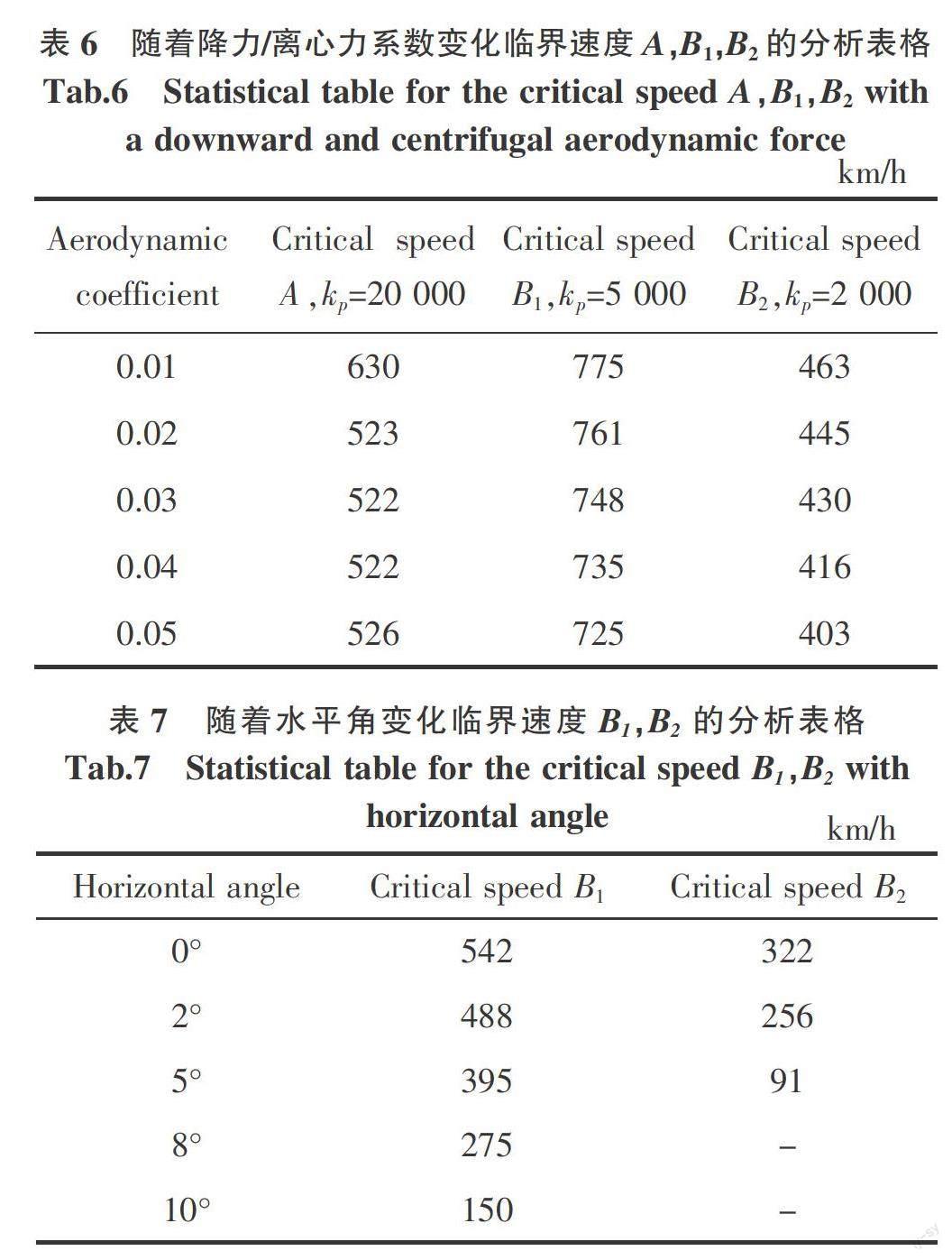
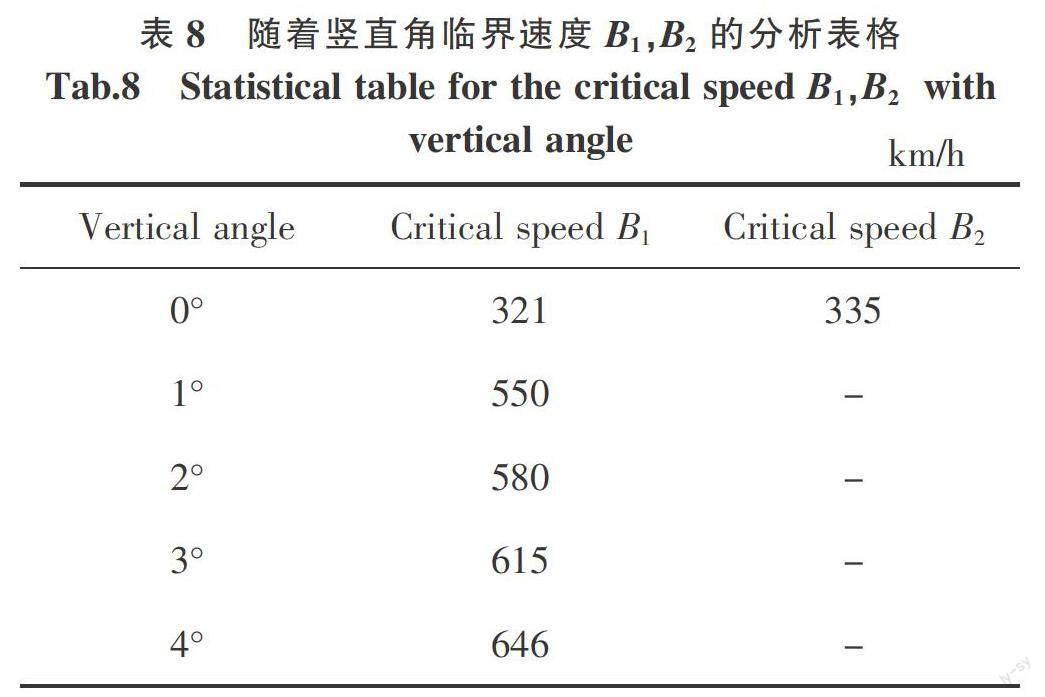
从表3～表5中可以看出：随着车速增加，临界速度A总体趋势减小，临界速度B1和B2增大。向心力作用下，随着水平角的增大，临界车速B1增大，临界车速B2减小;升力作用下，随着竖直角的增大，临界车速B1增大，临界车速B2减小。

3.3 临界速度存在的条件

正如3.1和3. 2部分讨论，当气动系数越小，第一类临界速度vcritical-A较大。当竖向坡度越大，第二类临界速度vcritical-B较大。

1） vcritical-A的平方根内的表达式为零是车速达到临界速度A的一个必要条件。

（-mcgcosβ）（cosα+sinα）+

（sinα-cosα）>0（12）

如果刚性导轨上的磁浮车系统中考虑气动荷载满足式（12）和气动力不考虑时或者车速为零，悬浮系统在平衡位置是稳定的。系统在平衡位置上的稳定性描述如下。当车速vvcritical-A，系统受到扰动不再收敛，发生极限环;当v=vcritical-A，系统的Hopf分叉发生了，系统达到了临界状态。

2） vcritical-B和vcritical-B的平方根内的表达式为零是车速达到临界速度B的一个必要条件。

-cosα+sinα+

mcgcosβcosα-（）2μ0AN2>0（13）

-sinα-cosα+

mcgcosβsinα-（）2μ0AN2>0（14）

如果刚性导轨上的磁浮车系统满足式（13）和式（14），气动力不考虑时或者车速为零，悬浮系统在平衡位置是稳定的。系统在平衡位置上的稳定性描述如下。当车速vvcritical-B，系统受到扰动不再收敛，发生极限环运动;当v=vcritical-B，系统的Hopf分叉发生了，系统达到了临界状态。

4 结论

1） 当在气动向心力工况时，第一类临界速度产生了。在这种情况下，临界速度随着位移控制参数的增加而减少;当在气动降力工况时，第二类临界速度产生了。不受控制速度反馈系数的影响。

2） 当磁浮车受到气动向心力和气动升力时，在水平角由0°增加到2°，临界速度B2由504 km/h降低到410 km/h;在竖直角由0°增加到4°，临界速度B2由500 km/h降低到278 km/h;气动升力系数由0.01增加到0.05，临界速度A1由620 km/h降低到530 km/h，临界速度B2由506 km/h增加到640 km/h。

3） 当磁浮车受到气动离心力和气动降力时，在水平角由0°增加到5°，临界速度B2由322 km/h降低到91 km/h;在竖直角由0°增加到1°，临界速度B2由335 km/h发展到无临界速度;气动升力系数由0.01增加到0.05，临界速度A1由630 km/h降低到526 km/h，临界速度B2由463 km/h减小到403 km/h。

参考文献：

[1] 吴晗，曾晓辉，史禾慕. 考虑间隙反馈控制时滞的磁浮车辆稳定性研究[J]. 力学学报，2019，51（2）：550-557.

WU H，ZENG X H，SHI H M. Stability analysis of maglev vehicle with delayed position feedback control[J]. Chinese

Journal of Theoretical and Applied Mechanics，2019，51（2）：550-557.

[2] 黎松奇，张昆仑，陈殷，等. 弹性轨道上磁浮车辆动力稳定性判断方法[J]. 交通运输工程学报，2015（1）：43-49.

LI S Q，ZHANG K L，CHEN Y，et al. Judgement method of maglev vehicle dynamic stability on flexible track[J]. Journal of Traffic and Transportation Engineering，2015（1）：43-49.

[3] 洪远卓，罗华军，佟来生，等. 新型四模块中低速磁浮车辆直线段运行稳定性研究[J]. 机车电传动，2020（6）：88-92.

HONG Y Z，LUO H J，TONG L S，et al. Study on operation stability of new four modules middle-low speed maglev vehicles on a straight track[J]. Electric Drive for Locomotives，2020（6）：88-92.

[4] 杨志安，崔佳磊. 基于MLP法的磁浮列车非线性系统的稳定性分析[J]. 唐山学院学报，2019 32（3）：1-7.

YANG Z A，CUI J L. Stability analysis of nonlinear systems in the maglev train based on MLP method[J]. Journal of Tangshan College，2019，32（3）：1-7.

[5] 洪华杰，李杰，张锰. EMS型磁浮列车系统滚动稳定性研究[J]. 控制工程，2006，13（4）：314-316.

HONG H J，LI J，ZHANG M. On the rolling stability of EMS maglev train system[J]. Control Engineering of China，2006，13（4）：314-316.

[6] 梁潇，马卫华，肖溪玥，等. 状态观测器参数对磁浮车辆悬浮稳定性影响的仿真研究[J]. 铁道科学与工程学报，2019，

16（4）：1026-1032.

LIANG X，MA W H，XIAO X Y，et al. Simulation research on the effect of stateobserver parameters on suspension stability of maglev vehicles[J]. Journal of Railway Science and Engineering，2019，16（4）：1026-1032.

[7] 黎松奇，张昆仑，刘国清，等. EMS型磁浮列车通过变坡点的稳定性研究[J]. 信息与控制，2015，44（4）：493-498.

LI S Q，ZHANG K L，LIU G Q，et al. The stability study of EMS-type magelv vehicle through grade change point[J]. Information and Control，2015，44（4）：493-498.

[8] 洪华杰，李杰，张锰. 磁浮车轨耦合系统稳定性分析[J]. 控制理论与应用，2006（3）：421-428.

HONG H J，LI J，ZHANG M. Stability analysis of magnetic levitation system with vehicle-guideway interaction[J]. Control Theory and Applications，2006（3）：421-428.

[9] 朴明伟，石得春，梁世宽，等. 高速磁浮车EMS主动控制的鲁棒稳定性分析[C]//北京：2005全国计算机辅助工程（CAE）技术与应用高级研讨会论文集，2005.

PIAO M W，SHI D C，LIANG S K，et al. Stability robustness analysis of high-speed maglev train′s EMS active control[C]//Beijing： Proceedings of 2005 National Advanced symposium on Computer Aided Engineering（CAE） Technology and Application，2005.

[10] 馬铁刚. 高速磁浮车主动悬浮导向控制稳定性研究[D]. 大连：大连交通大学，2005.

MA T G. The study on stability of levitation and guidance active control in high-speed maglev train[D]. Dalian：Dalian Jiaotong University，2005.

[11] 陈晓昊，马卫华. 控制器时滞对磁浮系统稳定性影响分析[J]. 机车电传动，2019（2）：139-147.

CHEN X H，MA W H. Analysis on the effect of controller time delay on the stability of maglev system[J]. Electric

Drive for Locomotives，2019（2）：139-147.

[12] 周又和，武建军，郑晓静，等. 磁浮列车的动力稳定性分析与Liapunov指数[J]. 力学学报，2000（1）：42-51.

ZHOU Y H，WU J J，ZHENG X J，et al. Analysis of dynamic stability for magnetic levitation vehicles by Liapunov characteristic number[J]. Acta Mechanica Sinica，2000（1）：42-51.

[13] 忽伟. 磁悬浮列车的运动稳定性研究[D]. 天津：河北工业大学，2014.

HU W. Research on motion stability of maglev vehicles[D]. TianJing：Heibei University of Technology，2014.

[14] 谢毅，寇峻瑜，余浩伟. 高速磁浮最小曲线半径及缓和曲线长度研究[J]. 铁道工程学报，2020（4）：43-48.

XIE Y，KOU J Y，YU H W. Research on the minimum plane curve radius and transition curve length of high-speed maglev[J]. Journal of Railway Engineering Society，2020（4）：43-48.

[15] 李茂春，郭庆升. 四悬浮架中低速磁浮车辆曲线通过分析[J]. 新型工业化，2021，11（3）：128-130.

LI M C，GUO Q S. Curve passing analysis of medium and low speed maglev vehicle with four suspension frames[J]. The Journal of New Industrialization，2021，11（3）：128-130.

[16] 王泽汉，杨新斌. 中低速磁浮车辆S形曲线通过性能分析[J]. 铁道车辆，2020，58（11）：1-3.

WANG Z H，YANG X B. Analysis of S-curve negotiation performances for medium-low speed maglev vehicles[J]. Railway Vehicle，2020，58（11）：1-3.

[17] 李东帅，黄靖宇. 基于深度学习的高速磁浮轨道不平顺预估[J]. 华东交通大学学报，2020，37（3）：44-51.

LI D S，HUANG J Y. Prediction of high-speed maglev track irregularity based on deep learning[J]. Journal of East China Jiaotong University，2020，37（3）：44-51.

[18] 时瑾，魏庆朝，鲍凤麒. 中低速磁浮交通圆曲线参数影响因素分析[J]. 都市快轨交通，2010（3）：68-71.

SHI J，WEI Q C，BAO F Q. Influence factors of circular curve parameters on medium and low speed maglev system [J]. Urban Fast Rail Transit，2010（3）：68-71.

[19] 黄志辉，高定刚. 常导中低速磁浮车辆竖曲线通过分析[J]. 铁道车辆，2005，43（11）：5-6.

HUANG Z H，GAO D G. Analysis of negotiation through vertical curves by magnetic levitation vehicles with common conductor and medium or low speed[J]. Railway Vehicle，2005，43（11）：5-6.

[20] 米隆，招阳，魏庆朝，等. 磁浮交通系统线路缓和曲线参数取值方法研究[J]. 北京交通大学学报，2007（4）：92-100.

MI L，ZHAO Y，WEI Q C，et al. Research on alignment parameters of high-speed maglev railway transaction curve [J]. Journal of Beijing Jiaotong University，2007（4）：92-100.

[21] 張耿，李杰. 低速磁浮列车竖曲线电磁力计算[J]. 中国电机工程学报，2012，32（3）：150-156.

ZHANG G，LI J. Calculation of electromagnetic force of low-speed maglev on a vertical curve[J]. Proceedings of the CSEE，2012，32（3）：150-156.

[22] 代一帆，刘万明. 高速磁浮平、竖曲线重叠地段线路参数研究[J]. 交通科学与工程，2019，35（2）：100-105.

DAI Y F，LIU W M. Research on alignment parameters of high-speed maglev at horizontal and vertical curve overlapped region[J]. Journal of Transport Science and Engineering，2019，35（2）：100-105.

[23] 李人憲，翟婉明. 磁悬浮列车横风稳定性的数值分析[J]. 交通运输工程学报，2001，1（1）：99-101.

LI R X，ZHAI W M. Numerical anlysis of crosswind stability of magnetically levitated trains[J]. Journal of Traffic and Transportation Engineering，2001，1（1）：99-101.

[24] WU H，ZENG X H，YU Y. Motion stability of high-speed maglev systems in consideration of aerodynamic effects：A study of a single magnetic suspension system[J]. Acta Mechanica Sinica（English Series），2017，33（6）：1084-1094.

[25] KWON S D，LEE J S，MOON J W，et al. Dynamic interaction analysis of urban transit maglev vehicle and guideway suspension bridge subjected to gusty wind[J]. Engineering Structures，2008，30（12）：3445-3456.

[26] YAU J D. Aerodynamic vibrations of a maglev vehicle running on flexible guide ways under oncoming wind actions[J]. Journal of Sound and Vibration，2010，329（10）：1743-1759.

[27] 武建军，史筱红. 横向风场作用下磁悬浮车体运动稳定性数值研究[J]. 兰州大学学报（自然科学版），2009，45（2）：96-102.

WU J J，SHI X H. Numerical analyses of dynamic stability of maglev vehicles in crosswind field[J]. Journal of Lanzhou University（Natural Sciences），2009，45（2）：96-102.