基于车桥耦合振动的公路梁桥行车舒适性分析

陈水生 葛世祺 桂水荣 赵辉

摘要：鑒于梁式桥行车舒适性差的特点，为探究过桥车辆在公路梁桥行驶过程中的乘坐舒适性，以一座梁式桥为分析对象，基于车桥耦合振动理论，进一步建立车桥耦合振动微分方程。采用自编车桥耦合MATLAB程序计算车辆座椅加速度，以国际标准ISO2631-1的加速度均方根值评价方法对司乘人员乘坐舒适性进行评价，分析车辆类型、乘坐位置、车重、桥面不平顺、车速等因素对车辆乘坐舒适性的影响。结果表明：不同的车辆类型，小汽车的行车舒适性优于货车和公交车;多排座椅的两轴公交车，前排座椅的乘坐舒适性比后排座椅的乘坐舒适性好且座椅距离车辆质心位置越远，乘坐舒适性就越好;不同乘客处于同排位置，站立乘客的舒适性要比座椅乘客的舒适性差;车辆乘坐舒适性对桥面路况等级很敏感，其随桥面路况的恶化而迅速降低;不同的车重，车辆乘坐舒适性随车重的增加而提高;车辆行驶速度对乘坐舒适性有一定的影响，但影响较小，为提高乘坐舒适性，建议对梁式桥的行驶车辆采取限速措施。

关键词：行车舒适性;车桥耦合;Newmark-β算法;加速度均方根值

中图分类号：U443.3 文献标志码：A

本文引用格式：陈水生，葛世祺，桂水荣，等. 基于车桥耦合振动的公路梁桥行车舒适性分析[J]. 华东交通大学学报，2023，40（1）：1-9.

Analysis on Driving Comfort of Highway Beam Bridge Based on

Vehicle-Bridge Coupling Vibration

Chen Shuisheng， Ge Shiqi， Gui Shuirong， Zhao Hui

（School of Civil Engineering and Architecture， East China Jiaotong University， Nanchang 330013， China）

Abstract：In view of the characteristics of the poor driving comfort for beam bridges， to explore the passing vehicle ride comfort in the process of driving on the highway bridge， a vehicle-bridge coupling vibration differential equation was established with a beam bridge as the analysis object， based on the theory of vehicle bridge coupling vibration. The seat acceleration of the vehicle was calculated by using the self-programmed vehicle bridge coupling MATLAB program， and the ride comfort of the driver and passenger was evaluated by the international standard ISO2631-1 root mean square acceleration value evaluation method. The influences of vehicle type， seat position， vehicle weight， bridge surface roughness， speed and other factors on the ride comfort of the vehicle were analyzed. The results show that the driving comfort of cars is better than that of trucks and buses for different vehicle types. For a two-axle bus with multiple rows of seats， the ride comfort of the front seat is better than that of the back seat in different riding positions， and the farther the seat is from the vehicle centroid， the more comfortable the ride is. If different passengers are in the same row， the comfort of standing passengers is worse than that of seat passengers. Vehicle ride comfort is very sensitive to bridge deck road condition， and it decreases rapidly with the deterioration of bridge deck road condition. For different vehicle weight， vehicle ride comfort increases with the increase of vehicle weight. Vehicle speed has a certain influence on ride comfort with less effect. It is suggested that beam bridge vehicle speed limit measures be taken in order to improve the ride comfort.

Key words： driving comfort; vehicle-bridge coupling; Newmark-β algorithm; root mean square value of acceleration

Citation format：CHEN S S，GE S Q，GUI S R，et al. Analysis on driving comfort of highway beam bridge based on vehicle-bridge coupling vibration[J]. Journal of East China Jiaotong University，2023，40（1）：1-9.

近年来，随着桥梁交通量的日趋增大，过桥车辆类型各异且车辆规格尺寸变的越来越复杂，在多种复杂因素的影响下，司乘人员的乘坐舒适性受到不同程度的影响。考虑以车桥耦合振动理论为基础的车辆乘坐舒适性研究很有必要，能为公路梁式桥的管养提供科学的依据，研究意义重大。

学者们对公路桥梁的乘坐舒适性也有研究，取得了很有价值的成果，如：王贵春等[1]应用ANSYS有限元软件模拟550 m福建长门大桥，运用D′Alembert原理建立9自由度三轴空间整车模型，分析桥梁在多车通过时考虑不同车速与车重下的动力响应与行车舒适性;吴庆雄等[2]以日本新西海桥为研究对象，对该桥的自由振动进行分析，建立考虑车辆与不平顺桥面相互作用力学模型，分析该桥在移动车辆作用下的冲击系数与行车舒适性;胡振东等[3]对过桥车辆的舒适性问题采用移动荷载简支梁模型，给出了车速与垂直加速度的影响关系，分析路桥过渡段及临界速度情况下车辆最大加速度;李雪红等[4]以某大跨度斜拉桥为研究对象，为提出大跨度桥梁行车舒适性评价标准进行实测，分析车辆驾驶员座椅振动特性，采集不同车速车内振动加速度有效值，结合国际通用标准ISO2631-1评价车内司乘人员人体客观感受，提出大跨度斜拉桥行车振动舒适性评价标准，并对该桥舒适性进行评价;韩万水等[5]在发展、完善颤振抖动的基础上，建立风-汽车、汽车-桥梁系统空间耦合振动力学模型，将风、车辆、桥梁三者作为一个相互作用的系统，并以杭州湾跨海大桥为工程背景，采用国际标准ISO2631-1对不同桥面不平顺下的车辆行车舒适性进行评价。

可以看出，上述学者的研究成果丰硕，但也存在如下不足：① 学者们主要侧重于大跨度桥梁的乘坐舒适性进行研究，对梁式桥的乘坐舒适性研究较少;② 现行的桥梁行车舒适研究中所采用的车辆模型多为7自由度整车，虽能反应行车舒适性所关心的车辆垂直、俯仰和侧倾振动，但未考虑座椅弹簧和阻尼对于舒适性的影响。因此，针对已有研究的不足，本文考虑座椅弹簧和阻尼的影响，根据D′Alembert原理详细推导了人-座椅-车辆振动方程。运用ANSYS软件建立20 m药湖高架桥的有限元模型，采用Newmark-β数值积分法求解座椅加速度，评价司乘人员的乘坐舒适性，并给出提高行车舒适性建议。

1 车桥耦合振动系统

1.1 车辆模型

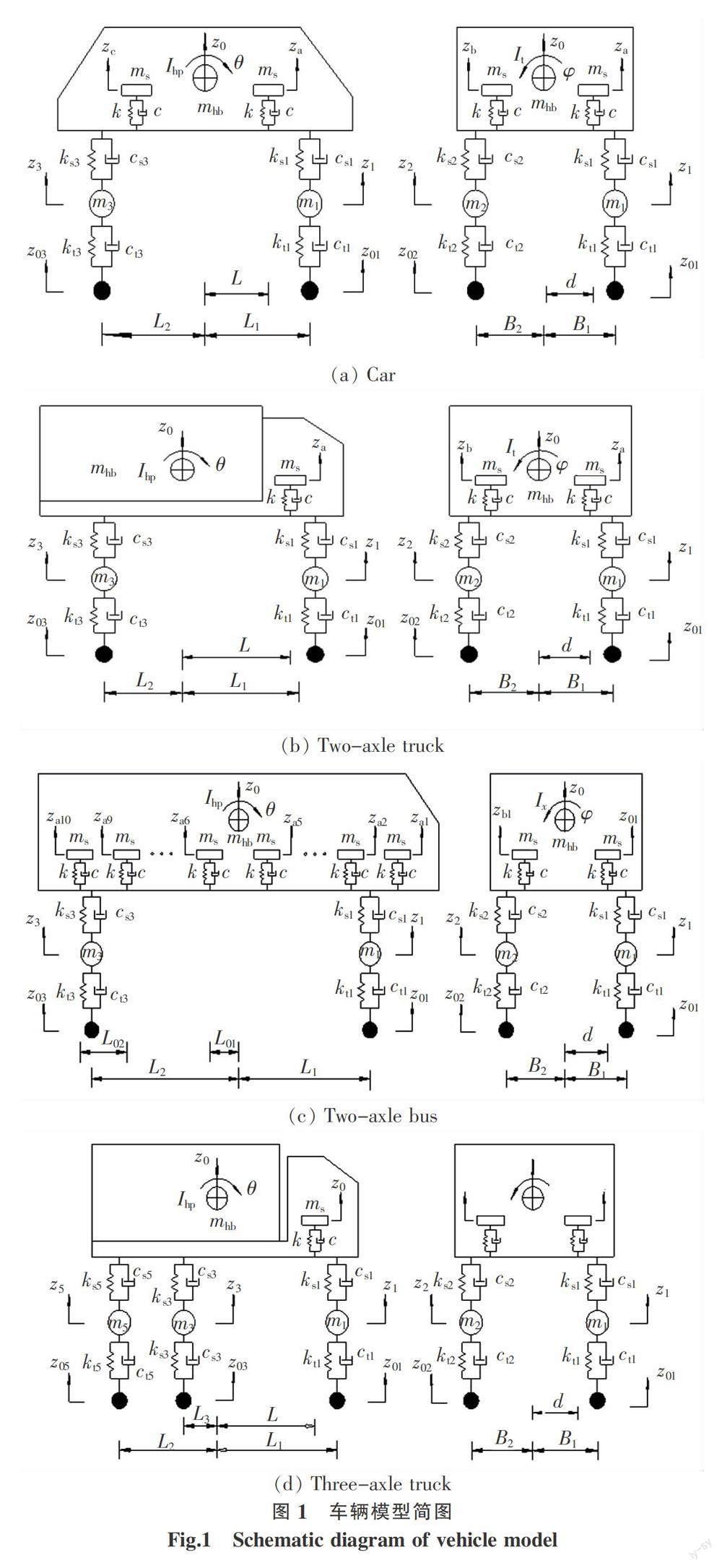
为了研究不同车型对行车舒适性造成的影响，以小汽车、两轴货车、两轴公交车和三轴货车为研究对象，详细推导了考虑座椅弹簧、阻尼的车辆振动微分方程，不同车辆模型的简图如图1所示[6-7]。

图1中的符号含义如下：z0为车辆垂直位移，m;θ为车辆俯仰转动角度，rad;φ为车辆侧倾转动角度，rad;Ihp为俯仰转动惯量，kg·m2;Ir为侧倾转动惯量，kg·m2;za，za为车辆座椅垂直位移，m;z1，z2，…，z6为车辆轮胎垂直位移，m;z01，z02，…，z06为地面不平顺位移输入，m;mhb为车辆总重，t;m1，m2为前轴轮胎质量，kg;m3，m4为中轴轮胎质量，kg;m5，m6为后轴轮胎质量，kg;ks1，ks2，…，ks6为上部弹簧刚度，kN/m;cs1，cs2，…，cs6为上部阻尼系数，kN/m;kt1，kt2，…，kt6为下部弹簧刚度，kN/m;ct1，ct2，…，ct6为下部阻尼系数，kN/m;ms为座椅质量，kg;k为座椅下部弹簧刚度，kN/m;c为座椅下部阻尼系数，kN/m;L1为前轴到车辆质心距离，m;L2为后轴到车辆质心距离，m;L3为中轴到车辆质心距离，m;L01为公交车中排座椅到车辆质心纵向距离，m;L02为公交车辆每排座椅间距，m;L为前后排座椅到车辆质心纵向距离，m;B1为前轴到右侧轮胎宽度，m;B2为前轴到左侧轮胎宽度，m;d为座椅到车辆质心横向距离，m。

根据D′Alembert原理建立不同类型车辆的振动方程，在此以两轴小汽车为例，建立其11自由度的车辆振动方程

Mv+Cv+KvZ=Fvint（1）

式中： Mv，Cv，Kv分别为车辆振動系统的质量、阻尼和刚度矩阵;Fvint为车辆振动作用下的各自由度的惯性列向量;Z为车辆的各自由度列向量，其中Z=[z1  z2  z3  z4  z0  θ  φ  za  zb  zc  zd]T。

1.2 桥梁模型

根据广义坐标离散的方法建立桥梁振动方程

Mb+Cb+Kbs=-Fvint-Fg （2）

式中：Mb，Cb，Kb分别为桥梁振动系统的质量、阻尼和刚度矩阵;Fvint为车辆振动过程中，车轮对桥面作用的惯性荷载向量;Fg为车辆重力荷载引起的各车轮作用点处向量;s为单元结点向量。

由于本文使用典型Rayleigh阻尼，模态空间取r阶模态，根据振型分解法有s=φiyi=Φy，根据模态综合法，对桥梁振动方程式（2）进行改写得

I+X+Ωy=-ΦT（Fvint+Fg）     （3）

式中：I，X，Ω分别为桥梁模型的广义质量、广义阻尼和广义刚度矩阵，其表达式如下：I=1

…

1，X=2ζ1ω1

…

2ζnωn，Ω=ω12

…

ωn2;

式中：ζn为桥梁第n阶阻尼比，本文将钢筋混凝土结构的阻尼比作为桥梁模型的阻尼比，阻尼比ζn大小设置为2%;ωn为桥梁第n阶自振频率;Φ为桥梁n阶振型向量矩阵;y为桥梁广义坐标列向量。

1.3 桥面不平顺

桥面不平顺是引起车-桥耦合系统振动的主要激励之一[8]，可分为竖向不平顺和横向不平顺。有研究表明[9-10]，当车辆行驶速度大于20 km/h时，横向桥面不平顺对车桥耦合振动影响较小。因此本文只考虑竖向桥面不平顺。通常情况下，桥面不平顺可视为平稳高斯随机过程，当过桥车辆以速度v匀速行驶时，其功率谱密度函数Gq（f）可以表示为

Gq（f）=2πGq（n0）n02（4）

式中：Gq（n0）为桥面不平顺系数，其值大小与桥面等级有关;n0为参考空间频率，n0=0.1 m-1; f为时间频率。

根据功率谱与幅值谱的关系，可以得到每一小段时间频率所对应的不平度幅值Ai，即Ai=Gq（fmid-i）·Δfi1/2，将m个小区间的Ai相叠加则可得到桥面不平顺的时域样本q（t）为

q（t）=Ai sin（2πfmid-it+θi）（5）

式中：fmid-i为每一小段时间频率的中值;θi为均匀分布在[0，2π]的随机变量。

1.4 车桥耦合振动模型

假定轮胎和桥面始终接触且不脱离[11-12]，考虑桥面不平顺的影响，通过轮胎与桥面接触处的作用力平衡条件和位移协调条件，建立车桥耦合方程，车辆的第i个车轮与桥面接触位置处的相互作用力可表示为

F=kti（-NΦy-qi+zi）+

cti（-vNi，xΦy-NΦy-i+i）+Fgi  （6）

将式（6）代入式（3）可得

I+（X-ΦTNiTctiNiΦ）+（Ω-ΦTNiT（ktiNΦ+

ctivNi，xΦ））y+ΦTNiTctizi+ΦTNi kti zi

=-ΦTNi（ktiqi+ctii）-ΦTNiTFi     （7）

联立式（1）和式（7），可得车桥耦合振动方程

Mbv+Cbv+Kbvu=Fg+Fw     （8）

式中：Mbv，Cbv，Kbv分別为车桥耦合振动系统的质量、阻尼和刚度矩阵;u为广义坐标列向量;Ni为车辆第i个车轮与桥面相互作用点处的位移场插值函数;Ni，x为Ni对车辆行驶方向的导数;nl为车轮数;Fg为车辆自重所引起的各车轮接触点处的荷载向量;Fw为路面不平顺随机激励作用于车轮和桥面接触点处的惯性荷载向量。

2 行车舒适性评价指标

当车辆在桥面行驶时，车辆振动通过座椅持续对驾驶员和乘客造成不同程度影响，导致司乘人员产生心理压力和焦躁不安，甚至会产生恶心、眩晕、操作能力下降。目前，行车舒适性的评价主要是基于人体对振动的感觉，其评价方法主要可以分为以下两种。

2.1 主观评价法

该方法主要根据乘客乘坐过程中的主观感受进行评价分析，通常由经过专门培训且经验丰富的评车工程师对车辆乘坐舒适性给出定性评价[13]。

2.2 客观评价法

主要有以下4种客观评价法：① 加速度均方根值法[14]，将不同频率下的座椅加速度均方根值进行频率加权，最后得到一个总的加速度均方根值作为评价指标;② K系数法[15]，考虑频率5 Hz以下的单向振动，且要求振动过程确定，实用性不强;③ 吸收功率法[16]，将人体竖向、横向的振动能量相加，用一个综合值表示，但该方法没有给出一个详细的评判标准，也未给出一个明确的舒适性界限，存在缺陷;④ 总体乘坐值法[17]，考虑了人体振动的12个分量，但所考虑的自由度数目过多，应用相对复杂，存在一定的局限性。

2.3 本文所采用的舒适性评价方法

综合比较上述方法的优缺点，在参考已有研究的基础上[17-18]，本文考虑采用加速度均方根值评价法，其表达式为

arms=          （9）

式中：arms为加速度均方根值;T为振动信号的持续时间;aw（t）为经过振动计权叠加后的振动信号加速度。

采用加速度均方根值评价法的主要计算步骤如下。

1） 对座椅加速度进行傅里叶变换（FFT），得到加速度功率谱密度函数。

2） 对不同频率下的加速度均方根值进行频率加权，所采用的竖向振动频率加权函数如下

wi（f）=0.5f 0.50 Hz≤f≤4 Hz

1        4 Hz≤f≤8 Hz

8/f       8 Hz≤f≤20 Hz（10）

arms=      （11）

式中： wi为频率加权系数;aw（i）为不同频率下的加速度均方根值。

3） 依据国际标准ISO2631-1对乘坐舒适性的评价标准，将总体加权加速度均方根值与历史数据进行对比（表1），完成车辆-人体舒适性评价。

3 实例分析

3.1 工程背景

以江西省昌樟高速公路的药湖高架桥为分析对象。该桥全长9 100 m，为装配式预应力空心板梁桥，单跨跨径20 m，横向布设8片梁。全桥桥面系采用主梁简支桥面连续结构体系，桥面铺装层采用10 cm的C40防水混凝土和4 cm沥青铺装层，每隔200 m设置伸缩缝一道，桥梁横断面如图2所示。

采用ANSYS有限元软件建立药湖高架桥的三维有限元模型，其中主梁和左右护栏采用实体单元Solid65，桥面铺装层采用壳单元Shell63，桥梁有限元模型如图3所示。ANSYS提取的桥梁前10阶频率与振型如表2所示。

3.2 行车舒适性影响因素分析

影响桥梁行车舒适性的因素较多，其中主要包括两个方面：一方面是桥梁结构参数对舒适性的影响，例如：不同桥型、不同桥梁结构几何参数等;另一方面为过桥车辆运行参数，例如：车辆类型、乘坐位置、车重和行车速度等。本文主要考虑过桥车辆的运行参数，着重分析不同车辆类型、乘坐位置、车重、桥面不平顺、车速这5种因素对药湖高架桥行车舒适性的影响。由于行车舒适性是一个累计量，车辆在桥面行驶时间不宜太短，取药湖高架桥的前10跨200 m进行行车舒适性研究。对于4种不同车型的过桥车辆，其中小车以前后2排座椅的加速度均方根均值表示车辆舒适性客观感受，而两轴货车、三轴货车则以司机座椅位置处的加速度均方根值评价车辆舒适性，最后两轴公交车则考虑前后10排座椅加速度均方根均值作为公交车辆舒适性评价指标。若无特殊说明的情况下，车辆行驶速度均取80 km/h，沿桥面中心线位置行驶，桥面不平顺等级设置为B级。

3.2.1 车辆类型

为了探究不同车型对行车舒适性的影响，图4给出了不同车型对座椅加速度峰值的影响。由图4可知：不同的车型的座椅加速度峰值从大到小依次为：两轴货车、三轴货车、两轴公交车、小车，其中两轴货车的加速度均方根值为0.338 m/s2，分别是小车、两轴公交车和三轴货车加速度均方根值的1.79倍、1.30倍和1.09倍。

在相同车辆行驶速度和桥面路况等级下，表3给出了不同车型对座椅加速度均方根值和舒适度的影响，由表3可知：不同车型的行车舒适性差异较大，行车舒适性由好到坏依次为小车、两轴公交车、三轴货车、两轴货车。依据表1加速度均方根值与人体客观感觉对应关系可以得出不同车型影响下的人体客观感受。即当乘客乘坐小车、两轴公交车或司机驾驶三轴货车时，人体的客观感受主要表现为没有不舒适;当司机驾驶两轴货车时，人体的客观感受则变为有一些不舒适。

3.2.2 乘坐位置

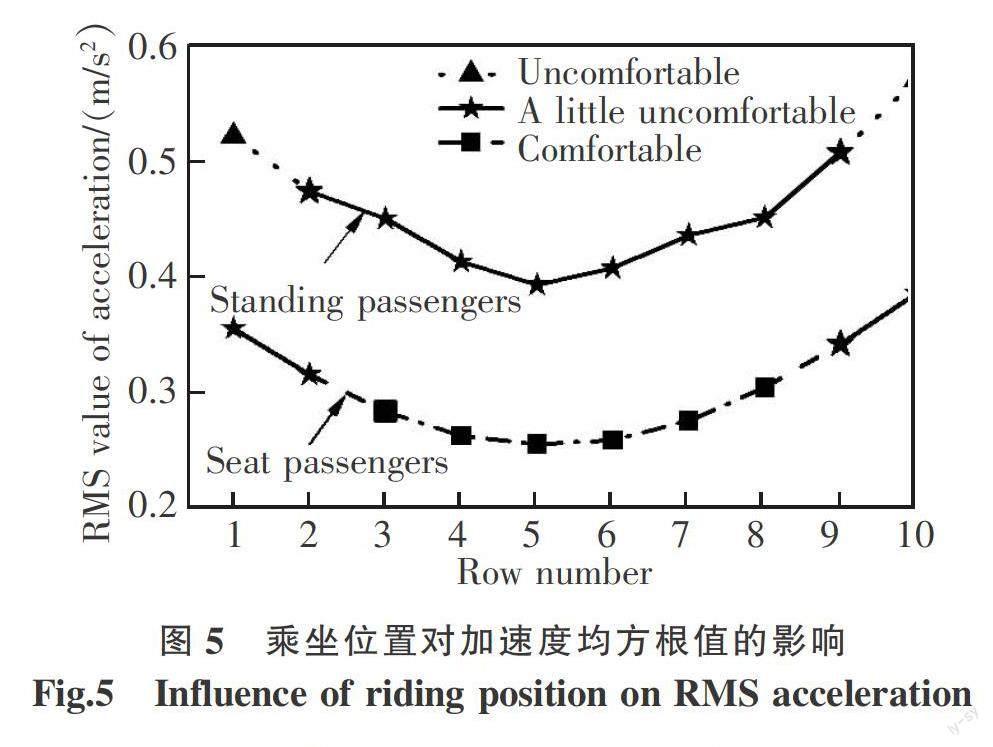
为了研究乘坐位置对行车舒适性的影響，以10排座椅的两轴公交车为例，图5给出了座椅乘客和站立乘客的加速度均方根值变化曲线。由图可知：① 行车舒适性对乘坐位置的变化较为敏感;第1、10排站立乘客的客观感受表现为不舒适，第2～9排站立乘客的客观感受表现为有一些不舒适;第1、2、9、10排座椅乘客的客观感受表现为有一些不舒适，其余排座椅乘客的客观感受表现为没有不舒适。② 同一车辆，无论是站立乘客还是座椅乘客，不同乘坐位置的舒适性感受是不相同的，具体表现为：车头和车尾位置的乘坐舒适性比车辆中部位置的乘坐舒适性差。这是因为车头、车尾位置到车辆质心的距离较大，在相同的激励条件下，车辆振动对车头、车尾位置的影响更大。

站立乘客的加速度均方根值范围介于0.392 ～ 0.569 m/s2之间，座椅乘客的加速度均方根值范围则介于0.255～ 0.385 m/s2之间，站立乘客的加速度均方根最小值大于座椅乘客的加速度均方根最大值，说明站立乘客的舒适性比座椅乘客的舒适性差，这是因为车辆行驶过程中，座椅对乘客所受振动具有减震效果。

3.2.3 车重

以两轴货车为研究对象，车体质量的取值范围为10 ～ 35 t。车重对座椅加速度均方根值的影响如图6 所示，由图6可知：座椅加速度均方根值随着车体质量的增加迅速减小，当车重增加到30 t时，座椅加速度均方根值与车重的关系近似呈现线性关系;司乘人员的乘坐舒适性也会随着车体质量的增加不断提高;当车体质量介于10～13 t之间时，司乘人员的客观感受表现为不舒适;当车体质量介于14～28 t 范围内时，司乘人员的客观感受表现为有一些不舒适;当车体质量大于28 t时，司乘人员的客观感受表现为没有不舒适。

3.2.4 桥面不平顺

有研究表明[19]，车桥耦合振动响应近似服从高斯随机过程，可以采用拉伊达法[20]对座椅加速度均方根值进行分析。以小汽车为研究对象，根据式（5）随机生成5 000组桥面不平顺样本，采用蒙特卡罗法对车辆振动响应进行统计分析，不同桥面等级对座椅加速度均方根均值和标准差值的影响如表4所示。由表4可知：① 随着桥面等级的降低，车体振动响应会剧烈增加，导致座椅加速度均方根均值不断增大;D级桥面路况的座椅加速度均方根均值最大，为0.675 m/s2，其值分别为A级、B级、C级桥面座椅加速度均方根均值的8倍、4倍、2倍;不同桥面等级的座椅加速度均方根标准差介于0.014～0.016之间，离散性较小。② 桥面不平顺直接决定了驾驶员和乘客乘坐舒适程度的好坏;当车辆在A级和B级桥面上行驶时，乘客的客观感受表现为没有不舒适的概率为99.73%;当车辆在C级桥面上行驶时，乘客的客观感受表现为有一些不舒适的概率为68.26%;当桥面等级为D级时，乘客的客观感受表现为不舒适的概率为99.73%。

3.2.5 车速

为研究车速对行车舒适性的影响，以小汽车为研究对象，不同车速对座椅加速度均方根值的影响如图7所示，由图7可知：随着车速的提高，座椅加速度均方根值和车速间近似呈现线性增长的关系;当车速处于30～140 km/h范围内时，座椅加速度均方根值始终小于0.315 m/s2，司乘人员客观感受主要表现为没有不舒适，但行车舒适性依然随着车速的增加而逐渐下降。

4 结论

本文基于车桥耦合振动理论，建立考虑桥面不平顺激励的人-座椅-车辆振动方程，使用MATLAB编制车桥耦合振动程序，计算车辆在行驶过程中的座椅加速度响应。采用加速度均方根值评价法并结合ISO2631-1完成舒适性客观感受评价，对不同影响因素下的移动车辆进行舒适度分析，可以得出以下主要结论。

1） 车辆类型对行车舒适性影响较大，在不考虑其他影响因素的条件下，小汽车的行车舒适性优于两轴货车、两轴公交车、三轴货车。

2） 两轴公交车中部位置的乘坐舒適性最佳，车头位置次之，车尾位置最差;站立乘客的舒适性感受要差于座椅乘客。

3） 车体重量的增加会使得舒适度不断提高，但是车重的增加也会致使惯性变大、制动距离变长，导致车辆间容易发生追尾事故，这是桥梁行车舒适性需要进一步研究的重点与难点。

4） 桥面不平顺直接决定了驾驶员和乘客乘坐舒适程度的好坏，随着桥面路况等级的降低，车桥耦合振动会愈发剧烈并严重影响桥梁行车安全与司乘人员乘坐舒适性。

5） 车速的提高会对司乘人员舒适性造成不利影响，但是影响程度相对较低。

参考文献：

[1] 王贵春，李武生. 基于车桥耦合振动的车辆舒适性分析[J]. 振动与冲击，2016，35（8）：224-230.

WANG G C，LI W S. Analysis on the vehicle ride comfort based on vehicle-bridge coupled vibration[J]. Journal of

Vibration and Shock，2016，35（8）：224-230.

[2] 吴庆雄，陈宝春，高桥和雄，等. 新西海桥的振动特性及舒适性评价研究[J]. 公路交通科技，2008（5）：61-67.

WU Q X，CHEN B C，KAZUO T，et al. Vehicle-bridge dynamic analysis and riding comfort evaluation of new saikai bridge[J]. Journal of Highway & Transportation Research & Development，2008（5）：61-67.

[3] 胡振东，王华林. 高速车辆过桥时的舒适性分析[J]. 振动与冲击，2002，21（4）：104-106.

HU Z D，WANG H L. Analysis of comfort properties for high-speed vehicle moving along bridge[J]. Journal of Vibration and Shock，2002，21（4）：104-105.

[4] 李雪红，周叶波，王仁贵，等. 大跨斜拉桥行车振动舒适性评价[J]. 公路，2011（11）：95-98.

LI X H，ZHOU Y B，WANG R G，et al. Evaluation of vibration comfort of long-span cable-stayed bridge[J]. Highway，2011（11）：95-98.

[5] 韩万水，陈艾荣. 风环境下大跨度斜拉桥上的车辆驾驶舒适性评价[J]. 中国公路学报，2008，21（2）：54-60.

HAN W S，CHEN A R. Ride comfort assessment of vehicles running on long-span cable-stayed bridge under crosswind[J]. China Journal of Highway and Transport，2008，21，（2）：54-60.

[6] 喻凡，林逸.汽车系统动力学[M]. 北京：机械工业出版社，2005.YU F，LIN Y. Vehicle system dynamics[M]. Beijing：China Machine Press，2005.

[7] SEKULIC D，DEDOVIC V，RUSOV S，et al. Analysis of vibration effects on the comfort of intercity bus users by oscillatory model with ten degrees of freedom[J]. Applied Mathematical Modelling，2013，37（18/19）：8629-8644.

[8] 陈水生，赵辉，李锦华，等. 车辆各轮相干桥面不平顺激励的车桥耦合振动[J]. 计算力学学报，2021，38（3）：393-400.

CHEN S S，ZHAO H，LI J H，et al. Vehicle bridge coupled vibration excited by vehicle wheel with coherent deck irregularity[J]. Chinese Journal of Computational Mechanics，2021，38（3）：393-400.

[9] 薛宇欣，周勇军，赵煜，等. 基于空间桥面不平顺的简支梁桥冲击系数研究[J]. 合肥工业大学学报（自然科学版），2021，44（3）：389-395.

XUE Y X，ZHOU Y J，ZHAO Y，et al. Research on dynamic load allowance of simply supported girder bridge based on spatial bridge deck roughness[J]. Journal of Hefei University of Technology（Natural Science Edition），2021，44（3）：389-395.

[10] 王刚强. 基于空间桥面不平顺的车辆-桥梁耦合系统响应分析[D]. 西安：长安大学，2020.

WANG G Q. Response analysis of vehicle-bridge coupling system based on spatial deck irregularity[D]. Xi′an：Chang′an University，2020.

[11] 桂水荣. 公路梁桥在移动荷载作用下車桥耦合振动响应研究[D]. 南昌：华东交通大学，2007.

GUI S R. Response study of road beam bridges subjected to moving load[D]. Nanchang：East China Jiaotong University，2007.

[12] 陈水生，付仂，桂水荣. 富山赣江特大桥车桥耦合振动响应及冲击系数研究[J]. 华东交通大学学报，2018，35（5）：27-34.

CHEN S S，FU L ，GUI S R. Study on vehicle-bridge coupling vibration response and impact coefficient of Ganjiang bridge in Fushan[J]. Journal of East China Jiaotong University，2018，35（5）：27-34.

[13] TENG T L，CHANG F A，PENG C P. Analysis of human body response to vibration using multi-body dynamicsmethod[J]. Proceedings of the Institution of Mechanical Engineers Part K Journal of Multi-body Dynamics，2006，220（3）：191-202.

[14] 陈代海，周帅，李整，等. 基于车致振动响应的双层钢桁梁桥行人舒适性分析[J]. 公路工程，2022，47（2）：7-13.

CHEN D H，ZHOU S，LI Z ，et al. Analysis of pedestrian comfort of double-deck steel truss bridge based on vehicle induced vibration response[J]. Highway Engineering，2022，47（2）：7-13.

[15] SUGGS C W，ABRAMS C F，STIKELEATHER L F. Application of a damped spring-mass human vibration simulator in vibration testing of vehicle seats[J]. Ergonomics，

1969，12（1）：79-90.

[16] 陈超，张玉新，邓继业，等. 工程车辆乘坐舒适性研究现状与关键技术[J]. 建筑机械，2012（1）：71-75.

CHEN C，ZHANG Y X，DENG J Y，et al. Research status and key technologies of construction vehicle ride comfort[J]. Construction Machinery，2012（1）：71-75.

[17] GRIFFIN M J. Non-vascular disorders associated with hand-transmitted vibration[J]. Handbook of Human Vibration，1990：595-608.

[18] 徐宁. 基于人-椅-车模型的舒适性评价及座椅参数优化[D]. 青岛：青岛大学，2019.

XU N. Comfort evaluation and seat parameter optimization based on human-chair-car model[D]. Qingdao：Qingdao University，2019.

[19] 朱思宇. 车—桥耦合系统振动的随机特性及极值分析（U1334201）[D]. 成都：西南交通大学，2017.

ZHU S Y. Random characteristics and extreme value analysis of vibration of vehicle-bridge coupling system（U1334201）[D]. Chengdu：Southwest Jiaotong University，2017.

[20] 熊艳艳，吴先球.粗大误差四种判别准则的比较和应用[J].大学物理实验，2010，23（1）：66-68.

XIONG Y Y，WU X Q. Comparison and application of four discriminant criteria for gross error[J]. University Physics Experiment，2010，23（1）：66-68.