运用“数字天平”理解反比例关系

文|周本圣

如何运用“数字天平”帮助学生更好地理解反比例关系？可以采用以下教学过程。

一、感知平衡现象

出示跷跷板、天平等图片。

提问：这几幅图都反映了一种什么样的现象？这里的平衡与什么有关？

记录学生表达出的关键词，如质量、大小、多少、距离、长度等。

二、实验探索规律

1.介绍数字天平

教师介绍：数字天平的两侧各有10个挂钩；挂钩之间的距离相等，按距离支点的远近分别是1-10 个单位；实验所提供的挂片都是等重的（如图1）。

图1

2.实验活动

挂片数量相同，位置也相同。

提出思考：如果两个挂片分别挂在位置5 的地方，你猜天平会不会保持平衡？学生动手操作，验证猜想。

继续猜想与验证：同时挂在“6”的位置呢？“8”呢？你们有什么发现？

预设学生发现只要两个挂片分别挂在相同的位置，天平保持平衡。

提出思考：两边各挂3 个挂片，怎么挂天平一定保持平衡？

预设学生发现3 个挂片放在一起，挂在相同位置上就一定能保持平衡。

证明 我们定义由引理2.2可知，f(x)的梯度f(x)的Lipschitz常数L=1且proxg=PC ,proxh=PD。则由三算子分裂

动手操作，验证猜想。

3.实验活动

挂片数量不同，位置也不同。

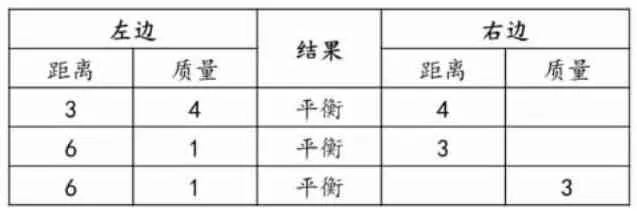
提出思考：如果在左边“3”处放4个挂片，在右边“4”处放几个挂片才能保证平衡？先猜测，再动手操作，把结果填入表中。

继续思考：如果在左边“6”处放1个挂片，在右边“3”处放几个挂片才能保持平衡？在“几”处放3 个挂片也能保持平衡呢？

填写表格，观察数据，寻找发现。

?

提出思考：填完上表，你有什么发现？

交流表达：3×4=4×3、6×1=3×2、6×1=2×3。

归纳板书：左边的距离×质量=右边的距离×质量。

教师追问：你发现要使天平保持平衡，距离和质量成什么比例关系？

组内交流，归纳小结：要使天平保持平衡，距离和质量成反比例关系。

三、体验反比例关系

1.先填写表格，再动手验证

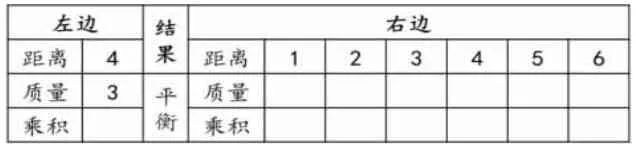
在左边“4”处放3 个挂片，在右边哪处放几个挂片才能保持平衡？

?

填写表格，再进行操作验证。

2.先判断结果，再操作验证

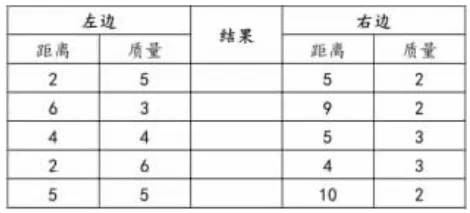
根据表格中的数据，先判断天平是否平衡，再操作验证。

?

3.介绍杠杆原理

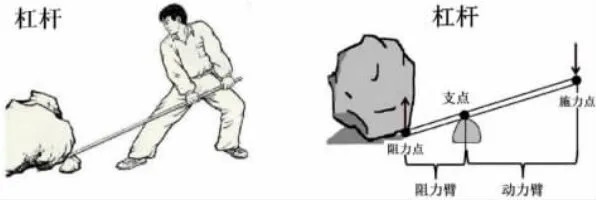
在“数字天平”的帮助下，学生经历“感知—猜想—验证—发现—归纳—应用”的实验探究过程，从特殊到一般，加深了对反比例关系的深度理解。