考虑注意力和时空特征深度学习的网约车行程时间预测

杨谊潇,邬群勇

(福州大学空间数据挖掘与信息共享教育部重点实验室,卫星空间信息技术综合应用国家地方联合工程研究中心,数字中国研究院(福建),福建 福州 350108)

0 引言

精确预测行程时间在道路导航、路径优化、乘客出行过程中扮演着重要的角色,但行程时间预测受到交通拥堵状态[1]、出发时刻、天气状况、驾驶人喜好等诸多因素的影响,很难准确预测.故研究精准的行程时间预测具有重要应用价值.精准、高效、可靠的行程时间预测模型一直是研究的热点,现有研究中,大多数研究者以期融入尽可能多的特征数据作为模型输入最大程度地还原应用场景,从数据驱动的角度着手进行行程时间预测,基于数据驱动的预测方法主要分为基于参数的机器学习方法和深度学习方法.基于参数的机器学习大都采用拟合回归的方式进行线性预测,一般适应于简单的数据形式.如文献[3]通过聚类分析和多项式拟合方法对历史轨迹数据进行建模,匹配与查询条件最近的历史模式.文献[4]采用自回归移动平均模型针对非平稳性的数据进行时间序列的建模,对于低时速、短距离的路段误差较大.文献[5]针对短距离交叉口的公交车辆行程时间预测采用多数据融合的方法,考虑单路段、多路段拟合进行实验,预测精度相比较有明显的提高.而深度学习主要通过现有神经网络结构的组合模型融入复杂数据进行时间预测.文献[6]提出卷积时空图注意力网络,将行程中的路段看为一个序列,通过设置一定大小卷积核的卷积网络去捕获子路段的空间信息,作为模型的输入去预测行程时间,能够更好地表征现实世界的场景.文献[7]提出了一种新颖的门控循环单元模型,将输入信息与隐藏状态信息在输入模型之前进行交互,并提出一个软残差结构设计进行时间预测,取得了很好的效果.基于路段的组合模型计算效率高,但随着路径长度的增加,预测精度会有所下降.Wang等[8]考虑时空信息、交通信息、个性化等辅助信息,提出一种新的基于路径的时间预测模型,由浅层线性层、深度神经网络、循环神经网络组成,相比较WD(wide deep)[9]模型能够很好地挖掘路段的局部信息.Duan等[10]考虑到数据获取的延迟,用长短期记忆(long short-term memory,LSTM)预测多个时间段的旅行时间,当观测到的旅行时间未被获取时,预测的旅行时间将被输入到模型中,弥补了数据稀疏问题.Hong等[11]提出一种异质结构信息的处理方法,将时间分为3个不同时间间隔(临近、一天、一周)作为模型的输入,可以很好地提取时间上的异质性信息.Li等[12]通过OD点提出一种多任务表征学习方法,支持在有限的信息下进行时间预测,但对数据量的大小要求很高.文献[13]采用长短期LSTM的方法从粗、细两种时间粒度去预测出租车短期时序的通行时间,但由于数据比较陈旧不具有时效性.

现有方法大多没有融合路径信息中的空间依赖性,较少关注交通拥堵变化对行程时间的影响,而严重的交通拥堵会导致时间预测的准确度大大降低,考虑交通拥堵变化对时间预测的影响,研究一种基于注意力机制的时空特征深度学习时间预测模型,利用卷积神经网络、注意力机制去捕获在交通过程中由于交通拥堵变化所产生的影响,通过长短期记忆网络去处理轨迹路段信息.为了能够平衡基于路段和端到端的预测方法,采用多任务学习机制去预测行程时间,最后通过全连接层输出总的时间预测信息.

1 数据和方法

1.1 数据

数据采用的是滴滴联合SIGSPATIAL共同在数据竞赛平台biendata发布的2020年8月17日至8月31日深圳市网约车订单数据,总共包括519 299条轨迹.以网约车单个订单数据的行程轨迹为数据集的基本单位,每个订单表示一条包含多个路段的轨迹,即路径.单条路径R是由多个路段组成,即{R1,R2,R3,…,Rn},n表示路段的个数.每个路段记录当前时刻(curr)和到达时刻(arriv)的拥堵状态.拥堵状态分为5个等级,由0、1、2、3、4表示不同路段的拥堵等级.当前时刻的拥堵状态表示为行程出发前每个路段的拥堵状况,到达时刻的拥堵状态表示车辆到达该路段的拥堵状态.单个路段的通行时间(lk_t)、长度(dist_gap)、路径所花费的总距离、总时间、行程出发时的天气状况、驾驶人编号(司机id)、路径的出行时刻等信息,如表1所示.

表1 数据集描述

1.2 方法

一种考虑交通拥堵变化的深度预测模型,如图1所示,模型主要分为4个部分: 基于卷积的路径时间距离特征提取、基于注意力机制的拥堵时间异常特征提取、时序模型时间预测和多任务学习机制.基于卷积的路径时间距离特征提取主要是通过卷积神经网络捕获路段中的时间、距离和交通拥堵状况信息;基于注意力机制的拥堵时间异常特征提取则是注重导致路径拥堵的交通路段信息;时序模型时间预测训练模型学习的路径信息,多任务学习机制是为了权衡预测路段与路径弊端的方法.考虑到路径发生中的背景信息,将天气、司机编号等信息输入到模型,丰富模型的内容.

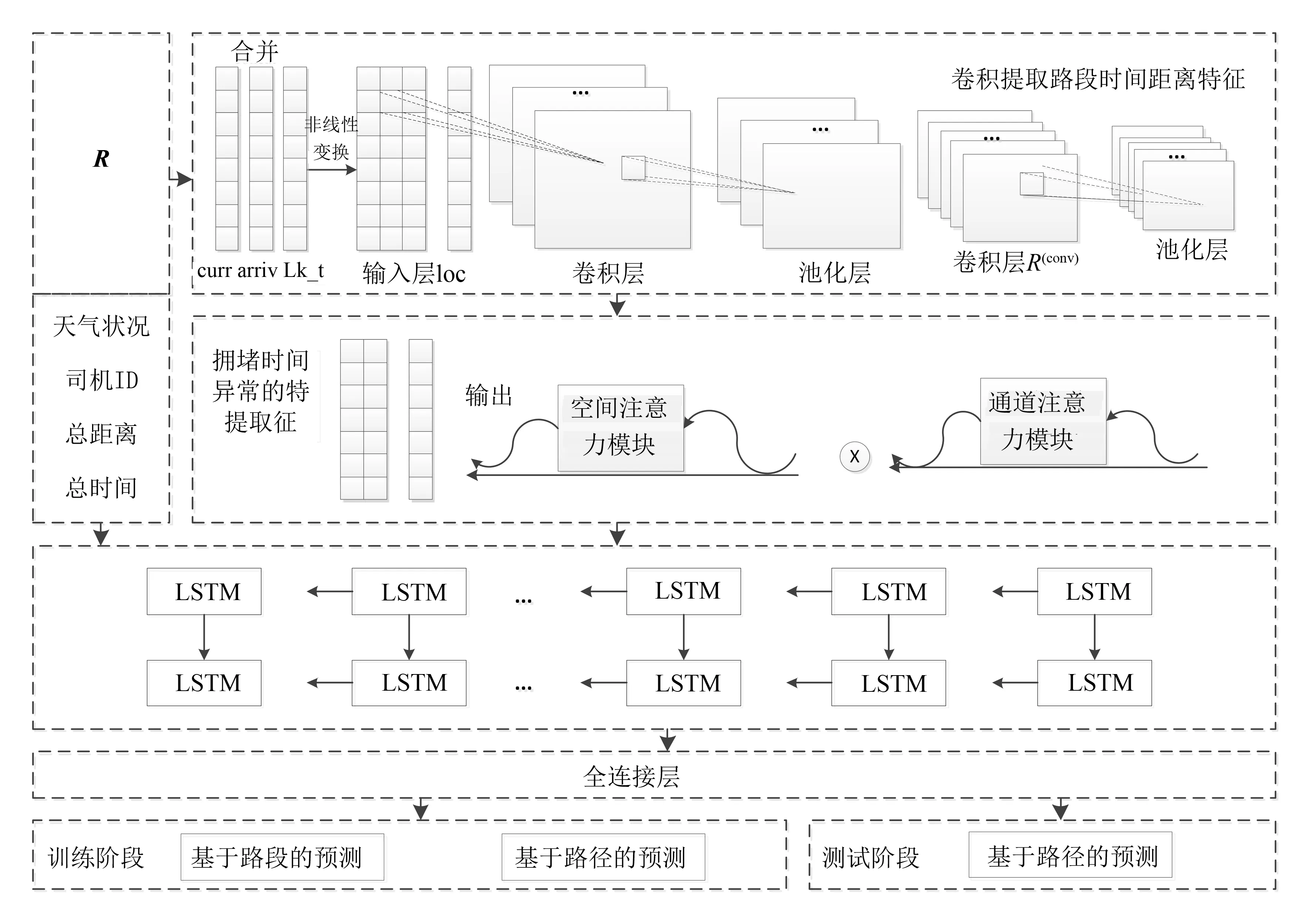
图1 模型结构Fig.1 Model structure

1.2.1基于卷积操作的路径特征信息提取

卷积层由多个卷积核组成,通过对输入数据进行卷积运算来提取路径过程中的特征信息.在行程过程中路段的拥堵状态、通行时间和路段的距离对于行程预测非常重要,不同的路况信息表示着车辆行驶的速度有差别,拥堵的交通状态则会造成车辆的逗留甚至停滞,增加了时间预测的难度.将路段的通行时间、距离、当前时刻和到达时刻路段拥堵状态连接作为卷积网络的输入.输入前,先将连接路段序列的特征矩阵通过一个非线性变换映射到高维空间R(cat)∈S(d),即d维的输入通道,每个输入通道作为一个特征监视器提取原始序列的路段特征信息,整个输出序列R(cat)∈S(|n| ×d),变换映射如公式(1),n表示路径中包含的路段数.为了提高模型的有效性,模型考虑了基于路段和基于路径的多任务学习机制,本文通过引入一个k×d的卷积核获得局部路段loc,loc∈S(|n-k+1| ×d),如R(cat).为了加深卷积网络的深度获得更大的感受野,充分提取路径中的特征信息,在卷积的过程中不断增加网络的通道数,具体的操作可以表示为loci和R(conv).通过对路段序列进行卷积运算,识别拥堵状态内在的信息来学习不同拥堵状态产生的影响,网络的输出out输入到注意力机制中.则有

R(cat)=tanh(Wloc·[R.curr∘R.arriv∘R.lk_t∘R.dist])

(1)

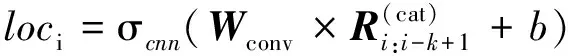
(2)

R(conv)=Maxpool(σcnn(Wconv1×loc+b1))

(3)

out=Maxpool(σcnn(Wconv2×R(conv)+b2))

(4)

其中:i表示路径中i_th路段;k表示卷积核的大小,取值为3;Wloc、Wconv、Wconv1、Wconv2表示可学习的权重矩阵;∘是合并运算;σcnn是ReLU激活函数;b、b1、b2是偏差.

1.2.2基于注意力机制的拥堵特征提取

为充分考虑交通拥堵所产生的通行时间异常,引入卷积块的注意力模块[14](convolutional block attention module,CBAM)机制,相比较SENet[15]网络的通道注意力模块,CBAM在通道和空间两个维度上进行卷积运算,卷积运算中每个通道都可以表征为特征监视器.通道注意力机制模块采用两个自适应的均值池化层和最大池化层同时对输入要素进行卷积操作,用来提取不同通道之间的关系,区分出不同通道的重要程度.为提取通道中更细致的特征信息采用最大池化的卷积运算作为补充,重点识别交通拥堵严重的路段信息.作为通道注意力模块的补充,空间注意力模块是将上述操作的输出作为输入应用均值池化和最大值池化,并将其连接输入到标准的卷积运算中获取空间信息.池化操作可以使通道中重要的信息高亮,卷积可以捕获哪些地方需要抑制或者强调,具体操作为

Mc(out)=σ(MLP(Avgpool(out))+MLP(Maxpool(out)))

(5)

Ms(out)=σ(f(k*k)([Avgpool(Mc(out));Maxpool(Mc(out))]))

(6)

其中:σ为sigmoid激活函数;Avgpool、Maxpool分别是均值池化和最大池化层;MLP是共享的多层感知机;k为卷积操作中的卷积核大小,取值为3.

1.2.3时序模型时间预测

长短期记忆网络(LSTM)解决了反向传播过程中梯度消失和梯度爆炸问题,具有较强的预测和容错能力.采用多层LSTM预测行程时间,通过调节输入门、遗忘门、输出门的比例系数去选择有多少信息被输入、更新、输出.不同的路径所包含的路段数量是不相等的,在进行路径预测的过程中输入的数据需要是一个定长的特征矩阵,采用一个线性变换映射到一个固定序列.在进行路径序列的预测过程中我们关注到增加路径的属性信息对于模型精度的提高有所帮助,因此在实验过程中引入司机id、总时间、总距离、天气状况等因素作为特征因子同拥堵特征提取后的输出out拼接后一同输入到LSTM中.LSTM隐藏状态的更新可以表示为{r1,r2,…,rn-k+1},具体操作为

ri=σrnn(Wx·outi+Wh·ri-1+Wa·attr)

(7)

其中:Wx、Wa、Wh为可学习权重;σrnn是非线性激活函数;ri为i_th局部路段的隐藏层;attr表示属性信息.

1.2.4多任务学习机制

多任务学习机制分别对局部路段和整条路径预测,为了提高预测的精度,在基于路径的预测中采用残差网络加深网络的层数,每个残差网络结构通过shorcuts将输入特征矩阵与输出特征矩阵相加.在实际出行预测中,不同的路段、路经的红绿灯个数对于轨迹花费的时间影响是不同的,采用自注意力机制对LSTM隐藏层进行权重的计算,重点预测通行时间较长的局部路段,采用softmax对隐藏状态ri赋予权重,动态更新权重参数旨在预测精确的通行时间,具体见ri.局部路径的预测采用多个全连接层进行结果的输出,LSTM通过对局部路段out1,out2,…,outi-k+1训练对应的输出r1,r2,…,ri-k+1进行时间预测,所预测的局部路段的通行时间表示为h1,h2,…,hi-k+1,这里的i表示第i个局部路段,r表示的是LSTM每个时间步的隐藏层.定义模型的损失函数为路径和路段预测的加权组合,具体公式为

ri=risoftmax(ri)

(8)

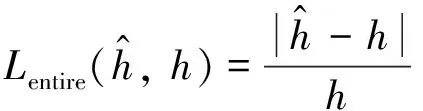
(9)

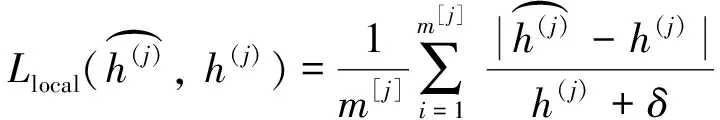
(10)

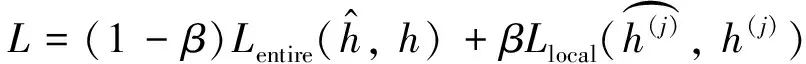
(11)

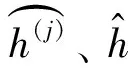
在模型训练阶段两者都采用,在测试阶段采用整条路径的预测结果代替模型的预测结果.

2 实验结果与分析

实验环境为: Windows 10操作系统,处理器为英特尔Core i7-10870H @ 2.20 GHz 八核,16 GB内存与512 GB固态硬盘,使用Python语言,在PyTorch框架下进行实验.采用2020年8月17—30日的8点到10点的数据作为训练集,用2020年8月31日8:00—10:00的订单数据进行验证.

模型引入的司机id、天气状况等数据不是数值型的,需要对其进行编码.较传统one-hot编码而言,embedding的编码方式对类别值特别大的属性特征可以有效降低维度,提高模型计算的效率;并且embedding的编码方式使数据间有了联系,相似的词语会有近似的语义信息,在编码空间会更接近.因此,采用embedding编码方式,将每个值通过一个参数矩阵映射到一个编码空间.

2.1 模型消融实验

模型的卷积核、注意力机制、LSTM预测的设置对于预测精度有重要的影响.实验通过改变卷积核k=3,5,7,相比较k=3,模型的精度分别降低了0.88%和0.71%,分析原因是实验数据维度较小,卷积核为3 的时候能够精确地学习到路段中的有效信息.采用包含和去掉自注意力机制模块进行对比实验,模型的预测误差分别为10.59%和12.72%,相比较前者精度降低了2.13%,证实自注意力机制对交通拥堵变化做出有效的关注.分别进行了一层、二层、三层的LSTM堆叠实验,结果表明层数的增加会增大内存开销和时间开销,但在层数的堆叠过程中预测效果没有提升,三层LSTM中结果相比较两层预测精度降低了1.08%.最终本文采用卷积核为3,基于注意力机制的双层LSTM模型作为最终的预测模型.

2.2 预测结果对比分析

2.2.1模型预测精度

实验采用平均绝对误差(MAE)和平均绝对百分比误差(MAPE)来验证模型精度.实验主要与随机森

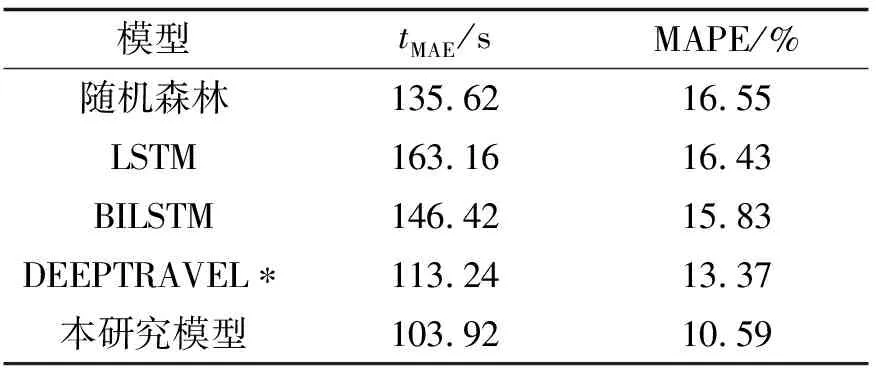
表2 不同模型的预测精度

林,LSTM网络模型、BILSTM网络(bi-directional long short-term memory)、DEEPTRAVEL作为对比,实验结果如表2所示.

从表2可以看出,随机森林与LSTM的模型预测基本一样,BILSTM模型的预测稍有提高,DEEPTRAVEL是基于改进后双向LSTM时间预测,精度又有进一步提升.模型实验表现明显优于上述模型,两个衡量指标均有明显的提升.相对于DEEPTRAVEL而言,MAE和MAPE分别提升了8.23%和20.79%.

2.2.2不同距离下的模型预测

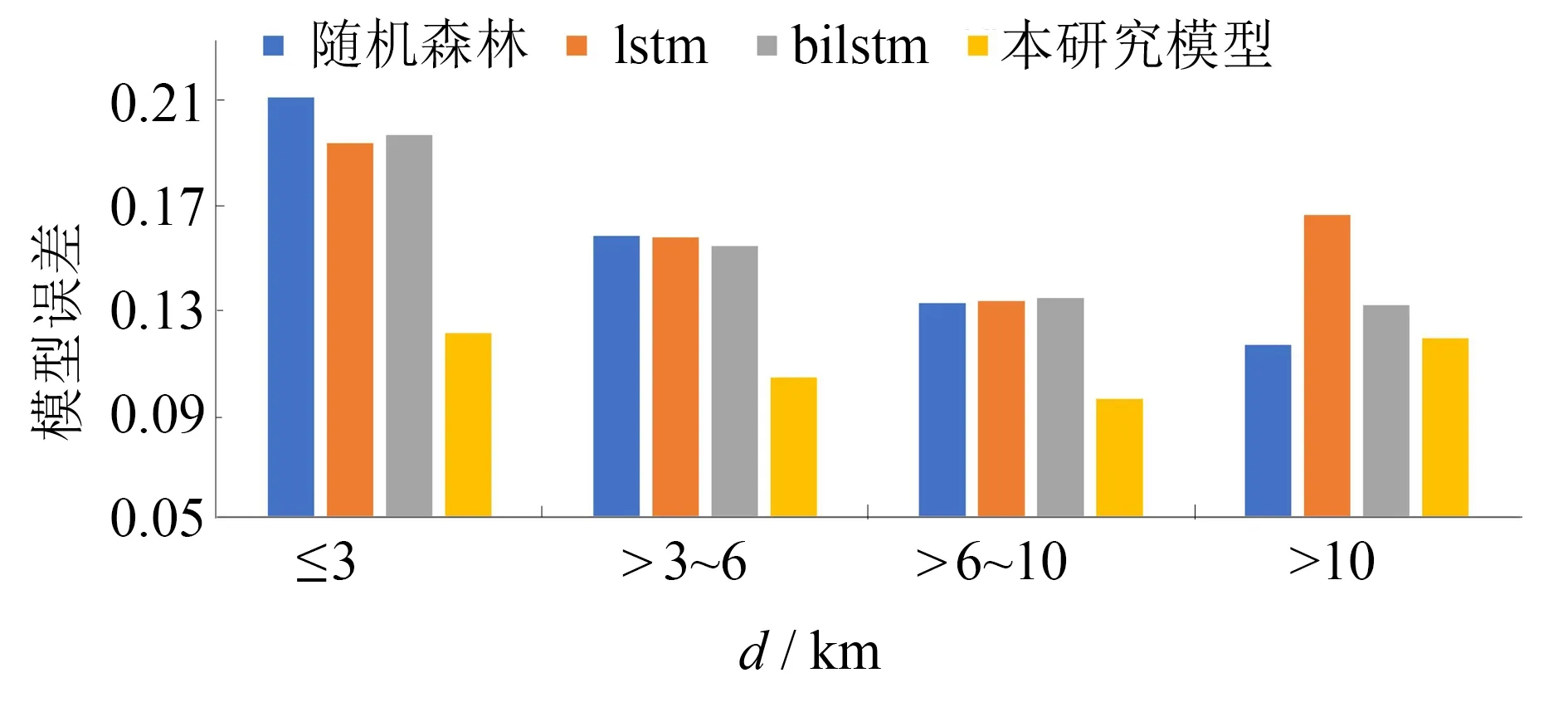
图2 不同距离下的模型预测误差Fig.2 Model prediction errors at different distances

随着轨迹序列的增加,模型的预测难度也逐渐增大.为了进一步验证模型的稳定性,针对不同距离的轨迹信息进行预测,为确保实验结果的准确性,采用每组实验平均30次的预测结果作为最终的预测结果.根据滴滴平台的计价规则,将距离划分为0～3、>3～6、>6～10 km,以及大于10 km的数据集,实验结果如图2所示.

从图2可以看到小于3 km的预测误差普遍偏高,这是由动态交通状态的局限性造成的,短途的轨迹数据预测难度更大,受交通状态的影响因素更严重,例如突发事件、交叉路口的延迟等等.相比较≤3、>3～6、>6～10 km的预测误差有所降低,但是超过一定的距离,LSTM与BILSTM的表现并不好.提出的模型则在不同距离的时间预测均表现出稳定精确的预测结果.图3给出了随机从测试集中抽取的50条轨迹数据真实值与预测值之间的误差,按照行驶时间从长到短进行排列.通过计算得知模型对轨迹的预测精度可以达到90%左右,充分证明模型的有效性.但从图中可以看出有些路径预测误差过大,通过查看数据集,发现这些轨迹数据有些是因为路径距离太长途径红绿灯数量较多,增加了路径的等待时间;有些路径是因为存在长时间停留在某个路段的状况,这种现象是很少见的.

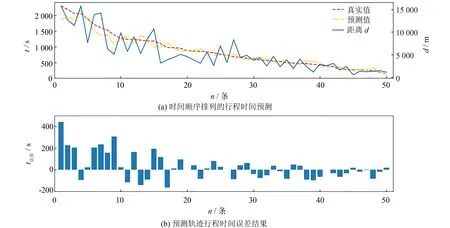
图3 随机50条轨迹预测结果展示Fig.3 50 random trajectory prediction results are displayed

2.2.3不同特征输入对比

表3 不同输入特征的预测精度

模型对不同的特征输入会有不同的表现,通过实验分别来验证其作用.ETA_time表示包含各路段通行时间和交通拥堵变化的特征输入;ETA_dist表示包含各路段的距离和交通拥堵变化的特征输入;ETA_td表示去除交通拥堵变化的特征;ETA表示输入完整的特征要素.实验结果如表3所示.从表3可以看出,所有的输入特征都发挥了重要的作用,其中路段距离要比路段时间特征效果更好,保留两个特征的ETA_td预测结果超过了ETA_time和ETA_dist,表明模型对于路径的特征提取距离和时间是非常有效的,完整的特征输入ETA输出结果最优,证实在到达时间预测的过程中考虑各路段的距离和通行时间、交通拥堵状态是非常必要的.

3 结语

集成多种机器学习结构去预测网约车的行程时间,提出一种新的深度学习模型.模型采用基于注意力机制的卷积神经网络,降低因交通拥堵状况对预测精度的影响,通过双层LSTM、多任务学习机制从路段和路径两个角度来预测旅行时间,以滴滴出行平台数据验证了模型的有效性.研究的主要结果如下.

1) 对比了其他机器学习的模型,在预测精度上有明显的提升,相比较文献[2]提出的DEEPTRAVEL,衡量指标MAE和MAPE分别提升了8.23%和20.79%.

2) 模型的预测首先取决于数据的选择,在实验中得出路段通行时间和距离对于通行时间预测影响很大,交通拥堵导致的通行时间异常也会导致预测的精度下降,模型在考虑交通拥堵变化的状况下预测精度提高了2.03%.

3) 验证模型对不同距离范围内的路径进行预测,模型在不同范围内的预测精度变化不大,证明模型可以适应不同距离的预测模式.

接下来将进一步采用图卷积优化模型实验,以期探索出一个更有针对性的深度学习模型.