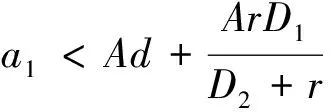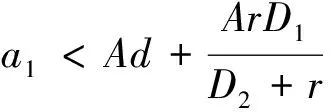非线性出生率对双斑块模型动力学行为的影响
朱紫睿,陈丽娟
(福州大学数学与统计学院,福建 福州 350108)
0 引言
种群在斑块间的扩散对种群的生存发展有着重要影响,近几年来,学者们对种群扩散模型的研究越来越多,并且得到了很多新颖的结果[1-7].例如,Huang等[8]研究了如下具有扩散的双斑块模型,即

(1)
其中:N1和N2为斑块1和2中物种的种群密度;参数D为扩散强度;s反应了扩散的不对称性.
学者们对单种群双斑块扩散模型的研究也取得了很大进展,文献[7]中提出了具有加法Allee效应的单种群双斑块扩散模型,即

(2)
其中:x1和x2为斑块1和2中物种的种群密度;m和a是Allee效应常数;D1(D2)代表从斑块1(2)到斑块2(1)的扩散率.其研究结果表明: 加法Allee效应和扩散率会导致种群或持久生存或灭绝,并且两个斑块内种群的总密度会随着a和D1的增大而增大,随m和D2的增大而减小,并且该系统存在鞍结分支.
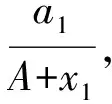
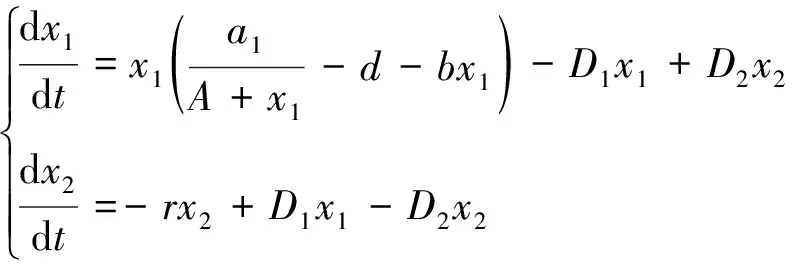
(3)

1 平衡点的存在性
对于系统(3),将讨论其平衡点的存在性,易知系统(3)始终有平衡点E0(0,0),其他平衡点可由以下方程组得到,即

(4)
为了得到系统的正平衡点,考虑由方程组(4)得到的方程为
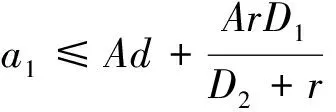
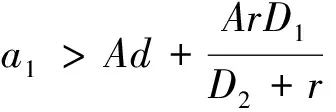
2 平衡点的稳定性
系统(3)在点E0(0,0)处的雅可比矩阵为
所以系统(3)在E0(0,0)处的雅可比矩阵的行列式和迹分别为


(5)

则系统(5)变为

(6)
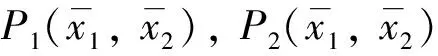
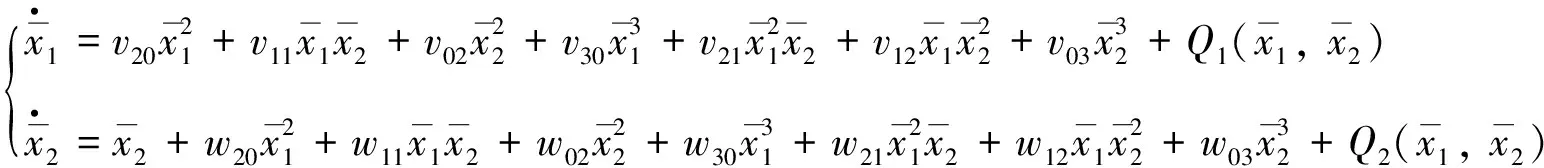
(7)


接下来,继续讨论正平衡点E*(x12,x22)的稳定性.系统(3)在点E*(x12,x22)处的雅可比矩阵为
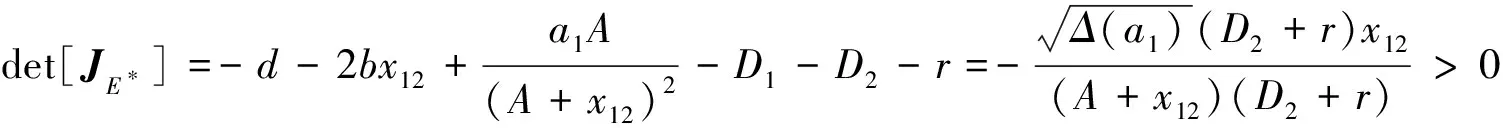

综上所述,可以得到以下定理.
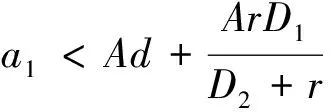

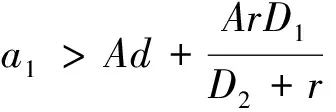
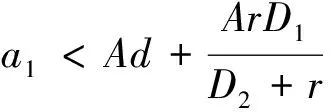
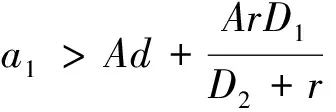
接下来将通过图1来验证定理2、推论1和推论2中的结论.

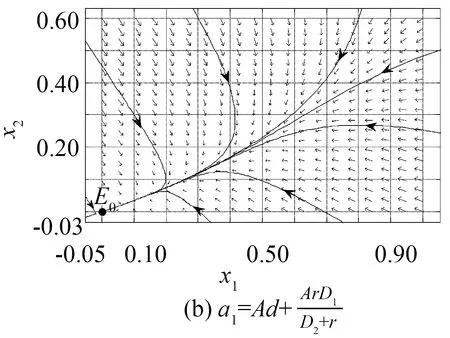
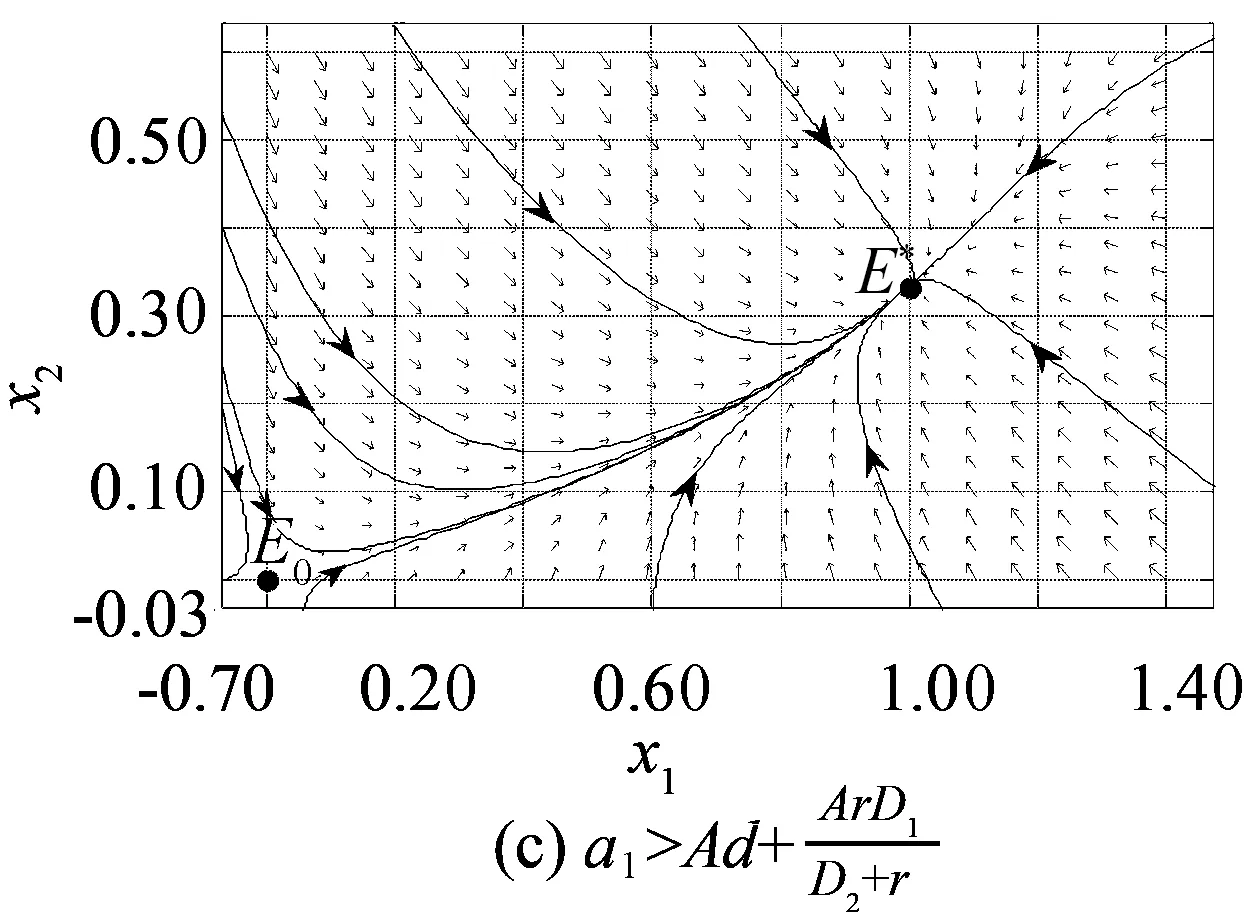
图1 系统(3)的相图
3 非线性出生率和扩散的影响
下面分别讨论非线性出生率和扩散对总种群密度的影响.由于有

接下来,通过数值模拟探究扩散对种群总密度的影响,令a1=3,A=2,D2=d=b=r=1,发现T1随着D1的增大而减小(具体见图2(a)).令a1=3,A=2,D1=d=b=r=1,发现T1随着D2的增大而增大(具体见图2(b)).这是符合生态学意义的,D1(D2)是从斑块1(2)到斑块2(1)的扩散率,当没有扩散时,斑块2内种群增长率是负的.因此,当D2变大时,种群更容易从斑块2扩散到斑块1中,即种群扩散到增长率更大的斑块,从而种群总密度增大,反之,当D1增大时,种群容易从斑块1扩散到斑块2中,这使得种群更容易灭绝,从而减少了种群总密度.


图2 扩散对系统(3)的种群总密度的影响
4 结论