考虑磨削热变形的表面微观形貌建模与仿真

胡宁 , ，陈海锋

（1. 湖南科技大学 难加工材料高效精密加工湖南省重点实验室，湖南湘潭 411201；2. 湖南科技大学 机电工程学院，湖南湘潭 411201）

表面微观形貌对工件的耐磨性、密封性及疲劳 寿命等使役性能起着关键作用，是磨削质量的重要评价指标之一，对磨削后工件的表面微观形貌进行预测与评价，按照建模方法的不同可分为经验模型和理论模型[1-2]。经验模型主要是通过大量实验总结得到加工参数与表面粗糙度参数之间的关联规律。刘金华等[3]采用多元非线性回归分析法建立关于加工工艺参数与齿轮齿面粗糙度之间的回归模型，并且通过单因素实验验证了模型的准确性。Alao 和Konnehr[4]建立了依据二次回归方程的单晶硅材料磨削表面粗糙度经验模型，通过数据拟合出磨削工艺参数和表面粗糙度之间的关系。经验模型具有预测准确、形式简单等优点，但需要大量实验数据作参考因子且有时所建立的回归模型只适用于一种特定材料，不具有普适性。相比于经验模型，理论模型通过数学方程去解释磨削的整个过程，能够将加工工艺参数的改变映射到输出的工件表面形貌建模上，以达到普适性的要求。梁志强等[5]将所建仿真砂轮形貌与实际扫描砂轮形貌进行对比，确定一定准确性后，运用拓扑法建立了关于理论的螺旋伞齿轮表面形貌模型，且仿真结果与实际也较为吻合。Zhou 等[6]采用硅胶粘合剂复制CBN砂轮磨粒形貌，以获得更加准确的砂轮磨粒形状，同时考虑了多颗磨粒切削轨迹之间的耕犁干涉问题，建立了工件表面微观形貌仿真模型。Wang 等[7]将砂轮磨粒设计成球形，将两侧耕犁截面简化为类抛物线，通过建立关于数学的理论模型，将工件表面的磨削形貌进行仿真研究。张升武[8]建立了考虑自激振动的磨削工件表面微观形貌理论仿真模型，从理论角度分析动态接触刚度、接触载荷及阻尼对磨削形貌的影响规律。

目前，国内外学者在理论建模时主要考虑了耕犁滑擦、自激振动的影响，然而，除了上述因素外，磨削过程中产生热变形对表面微观形貌也会有一定的影响。张勇等[9]在对圆柱体零件进行磨削实验时发现，零件较薄的表层存在一定的热变形。李通[10]对60 mm 长的40Cr 钢在磨削后的截面进行测量，发现当磨削温度达到120 ℃时，磨削热产生的变形量达到了67 μm，且变形量随着磨削热的持续上升呈线性增长。因此，研究考虑磨削热变形的表面微观形貌建模方法，对优化磨削加工参数以获得更好的表面质量具有重要的理论意义和工程价值。

1 砂轮表面形貌建模

砂轮表面的微观形貌是影响工件磨削材料去除的重要因素，砂轮自身的磨粒分布情况、磨粒相对大小以及磨粒所呈现的形状等属性决定了工件磨削后的表面质量。虽然砂轮实际磨粒形状复杂多变，但是考虑到磨粒本身存在正前角，因此将砂轮形貌磨粒假设为关于半球体内接的四面体也是具有一定合理性的[11]（如图1 为磨粒切削截面）。在砂轮仿真建模过程中，设置磨粒度号M= 120，组织号S= 8，并且砂轮整体采用半径r0= 50 mm，宽度b= 10 mm进行研究。

图1 考虑磨削热变形的磨削示意图

根据文献[12]可知，磨粒最大直径、磨粒平均直径为：

式中：dg,max为最大磨粒直径；dg,ave为平均磨粒直径；µ为 均值； σ为标准差。

根据Doman 等[13]提出的磨粒切刃高度服从高斯正态分布因此在建立砂轮模型过程中，假定由砂轮磨粒大小影响并决定磨粒分布状态，设定切刃的露出高度符合正态分布即h的分布函数为

同时假定砂轮表面相邻磨粒之间平均间距为

式 中：dg,i,j,k和dg,l,m,n分 别 为 磨 粒Gi,j,k和Gl,m,n的 直径。如不满足上述条件，需将Gl,m,n重新赋值并计算。

2 考虑磨削热变形的表面微观形貌建模方法

磨削加工的过程可以分为滑擦、耕犁和切削3 个阶段，由于磨削热的影响，磨粒与工件接触过后产生的切削和耕犁部分会随之发生变化，进而影响工件的整个表面磨削微观形貌的粗糙度。已有研究表明[14]，耕犁效应表现为实时切削的磨粒部分将工件材料挤压堆积至两侧形成隆起状，且研究认为每侧耕犁隆起部分的面积与切削效率和实时切削截面的面积有关，在此基础上，考虑到磨削热引起的弹性恢复形变，冷却后，磨料切削形成的截面将向内收缩。如图1 中实现所示，本文将磨削热引起的弹性收缩变形量假设为实时切削部分的12.5%，并以此进行理论的研究。

2.1 考虑磨削热变形的单颗磨粒三维轨迹建模

如图1 所示，为了方便研究与建模，将隆起部分设为三角形，并且每一侧隆起部分的面积Ap与磨粒的实时切削面积Si呈一定比例关系[15]为

式中ζ 为切削效率比，本文选择ζ =0.75%。

图1中S为实时切削截面面积，因此由图1 中所示的磨粒截面几何关系整理为

式中：a为一半的耕犁底边；h为 耕犁的高度；H为实时切削磨粒的三角底边；as为实时切削磨粒部分的高度值；H和as同a和h一样可以按一定比例可以相互表示。

为了描述单颗磨粒G 的实时切削状态，对yoz平面的切削截面进行分析。磨粒切削实时截面图如图2 所示。

从短期来看，分类监管之下，监管部门通过对III类村镇银行监管强度的提高，降低其贷款违约的平均概率，提高其预期收益率水平，进而带来预期收益上升的激励效应，但是由于银行自身不合规贷款规模较大，监管强度的提高使得此类村镇银行贷款规模迅速下降，进而造成预期收益下降的激励负向反馈;同理，对Ⅰ类村镇银行降低监管强度能够通过提高其贷款规模水平从而带来预期收益上升的激励效应，同时也会造成其贷款违约概率上升引致抑制预期收益上升的激励负向反馈，E+、E－则分别代表分类监管为村镇银行整体带来的激励正效应与负效应。

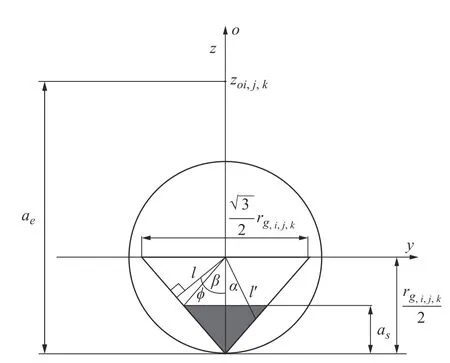
图2 磨粒切削实时截面图

阴影部分为实时切削部分as， β作为实时切削的最大阈值的存在。当 α无 限逼近 β时，可由几何关系推导出as与 β之间的关系，同时考虑磨削热变形对理论切削的影响，并且在计算yoz截面的理论公式的同时将耕犁和磨削热变形的影响以高度值的方式统一表现出来，故可得：

式中：rg,i,j,k为磨粒G的直径；as为磨粒实时切入深度，其与磨粒中心的切削轨迹有关，对于磨粒G 其切削轨迹最低点到坐标原点的距离表示为r0+在切削区域内的圆心坐标表示为zo,i,j,k。根据图2 位置关系可得

式中：ae为实际切削深度；r0为 砂轮半径；ap为理论切削深度。

由于砂轮在实际加工切削对刀时，是以试切火花为基准进给，再以预定的切削深度进给，因此实际切削深度可表示为

式中rg,max为最大磨粒直径。

与此同时，在砂轮磨削过程中，如图1 所示，建立关于砂轮坐标系o-xyz以及对应的极坐标。磨粒G 在砂轮上的位置可表示为以及极坐标此处砂轮为顺时针工作，整体磨粒均呈现逆磨状态，同时结合图1 中砂轮工作的几何关系，可得出关于xoz平面的单颗磨粒G 的运动轨迹：

式中：x和z分别为磨粒G 在轨迹中的瞬时位置坐标；ω为磨粒G 在工件上的工作角速度；vw为工件相对进给速率；t为砂轮相对工作时间。

设不同磨粒之间的相位差为 φ/ω，式（11）可写为：

对应的，将图1 中所示yoz截面的考虑磨削热变形的相对轨迹方程式（8）和式（12）进行联立，得到考虑耕犁和磨削热变形的单颗磨粒G 的三维轨迹方程为：

通过对上述方程的计算，得到单颗磨粒G 的三维轨迹切削图，如图3 所示。

2.2 磨削表面微观形貌生成

在计算得到单颗磨粒G 的三维轨迹方程后，选用将工件表面划分为多个网格，并将网格点上对应的高度值进行输入，最终生成表面形貌的方法。该方法的基本思想为：

1） 首先根据砂轮仿真形貌和所输入的加工工艺参数的情况下，通过式（13）求出每颗磨粒在所经历的切削轨迹上的每一点的坐标值以及其在xoy平面上的映射值；

2）将工件表面进行网格划分，网格之间的间距根据所设置的仿真精度进行确定，在本文中，所选用精度为5 μm，工件xoy表面的网格点坐标采用表示，同时为了考虑工件的原始平面状况，每个网格点的初始高度值用表示；

3） 由于砂轮磨粒在工件xoy表面上的映射不是均匀分布的，单个网格点上所经历的磨粒个数是相对有限的，因此为了提升计算机的计算效率，以其网格点为中心，取一个矩形的搜索范围，然后将所经过区域范围内的磨粒视作与平面点相互匹配的点，最后通过计算机计算这些匹配点的最低高度值；4）依次对工件表面所有网格点重复以上操作，求得每个网格点上所匹配到的磨粒个数所经历的轨迹最低点，并对其进行最低值的筛选，赋值到对应网格点的高度值该高度值的上标表示为砂轮磨粒的位置，下标表示工件表面网格点的坐标。然后将这些高度值进行连接并形成磨削工件表面的微观形貌。因此，所建立的平面工件磨削表面形貌仿真流程图如图4 所示。

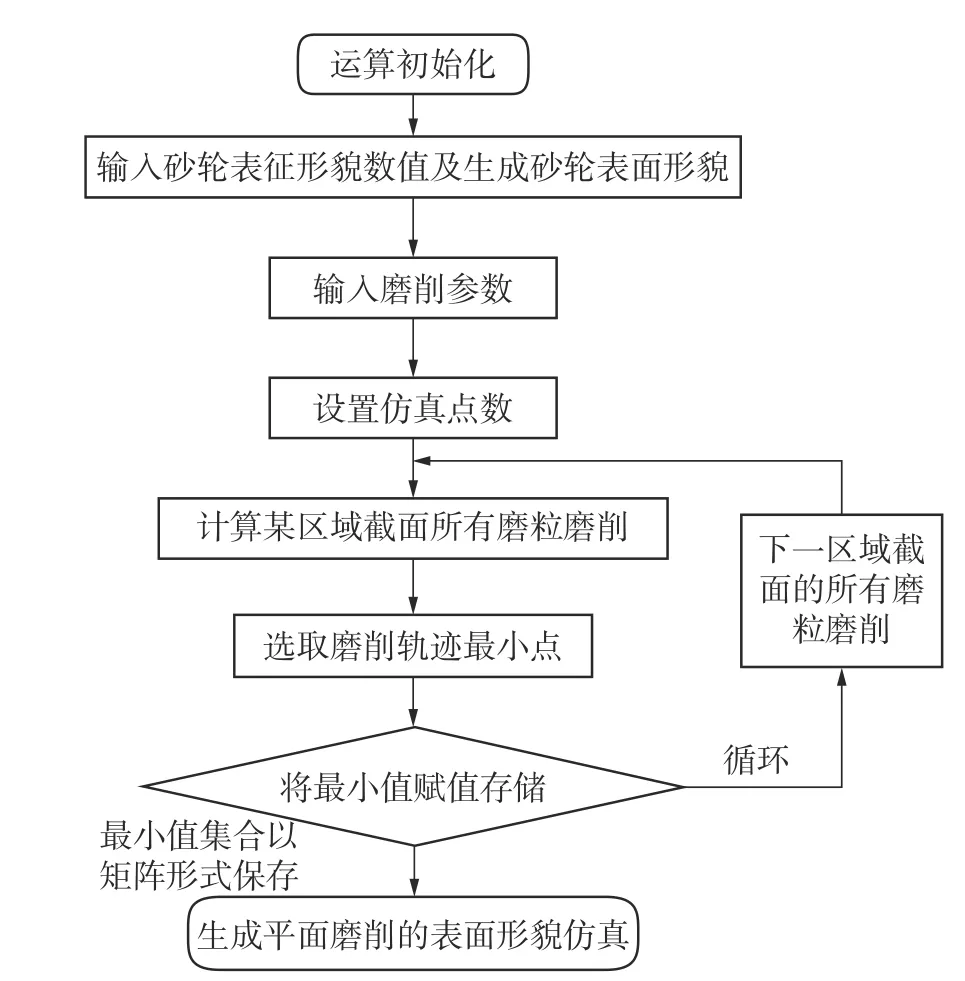
图4 平面工件磨削表面形貌仿真流程

3 实验验证

3.1 齿轮钢平面磨削实验

为验证仿真模型的正确性，采用VMC850 立式数控加工机床对1 2Gr2Ni4A（长16 mm、宽9 mm、高9 mm）材料进行平面磨削实验，实验装置如图5 所示，加工工艺参数如表1 所示。磨削加工完成后，对工件进行清洗，采用白光干涉仪（VeecoWyko NT9100）对工件表面微观形貌进行观测。

表1 干研磨磨削加工参数

图5 齿轮钢平面磨削装置

3.2 磨削仿真与实验对比分析

采用与实验相同的加工工艺参数进行仿真，得到仿真形貌如图6 所示。对比发现所建仿真形貌图与文献[7]中的形貌图两者基本一致，且考虑磨削热变形下的表面微观形貌仿真粗糙度误差最大为13.31%，因此可知本文所建考虑磨削热变形的平面磨削微观形貌是具有一定准确性的。针对图7 和 图8以及表2 的仿真粗糙度与实验所得粗糙度之间的比较，随着砂轮转速的提升，工件表面仿真形貌逐渐趋于平整，峰值高度也有明显下降，整体表现与实验结果也是相当吻合；随着磨削深度的不断增加，仿真的工件表面粗糙度与实验结果均有所上升。对此可推测原因是砂轮转速增加的情况下对于砂轮磨粒在单位时间内有效工作切削次数的增多，多个磨粒累计作用下，工件表面残余高度趋于稳定且减小，因而工件表面整体质量得到改善。当砂轮磨削深度增加时，所参与的磨粒增多，其中大颗的磨粒能有更多机会参与切削，不仅如此磨削深度的增加会产生更加剧烈的磨削热变形，从而提升表面微观形貌的粗糙度。

表2 关于实验与仿真结果之间的粗糙度对比表

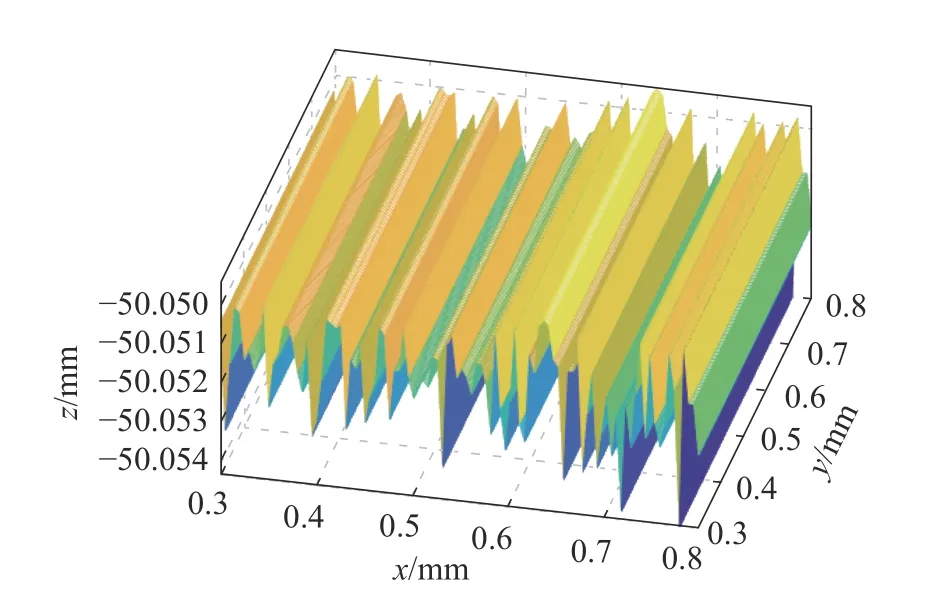
图6 考虑磨削热变形的优化仿真微观形貌

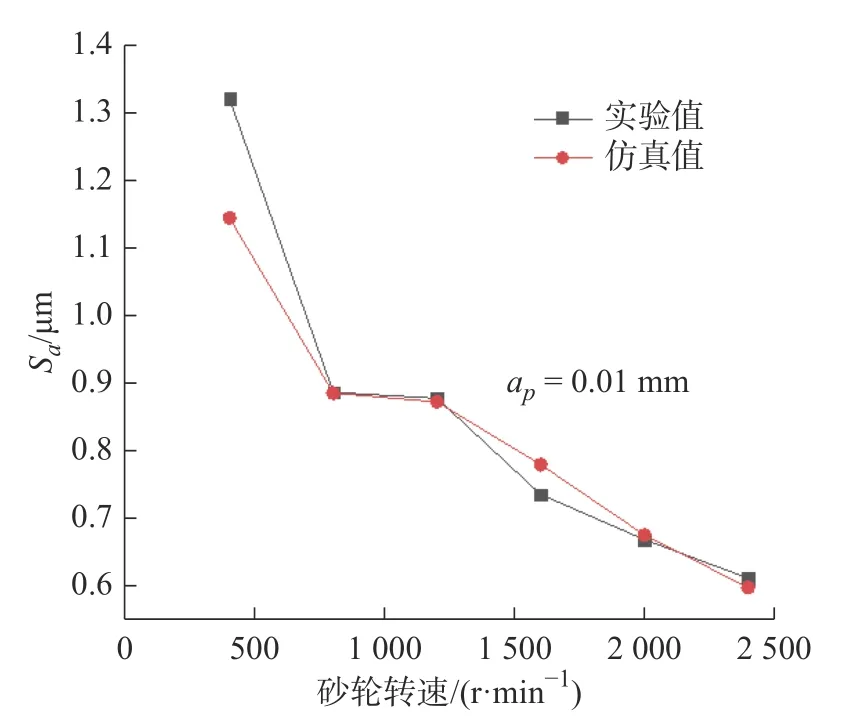
图7 不同砂轮转速下实验与仿真粗糙度

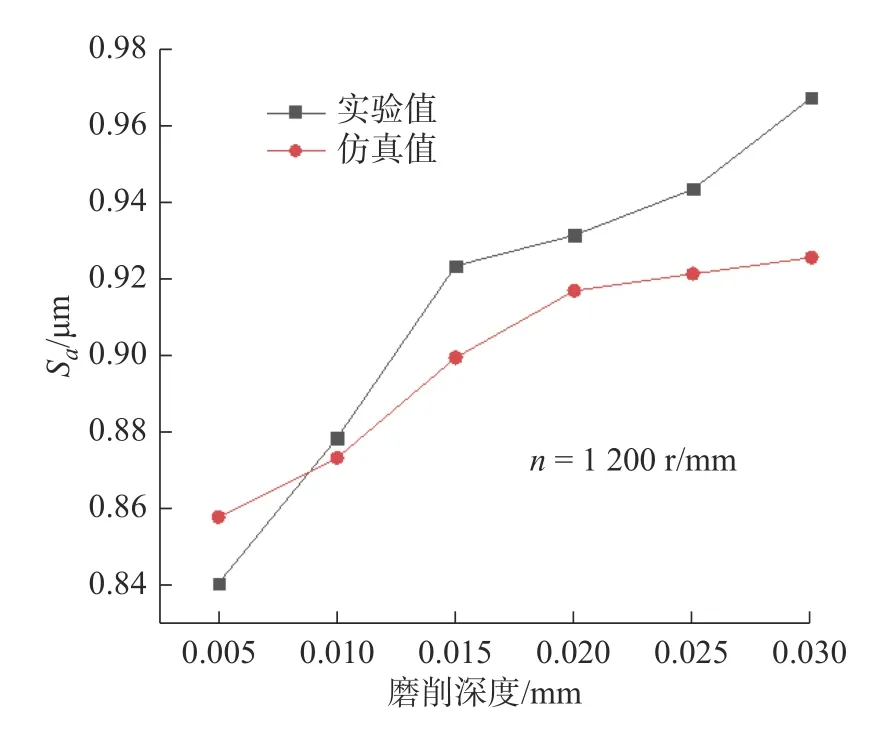
图8 不同磨削深度下实验与仿真粗糙度

虽然所提出的磨削热变形影响下的模型相比实验所得粗糙度的数据结果有所接近，但在相对较低转速400 r/min 情况下仍存在不小误差。针对这一现状分析在实际加工过程中，磨粒切削挤压工件，导致表面材料发生塑性变形，两侧隆起部分对原本切削后留下的轨迹凹坑进行了填补，甚至对之前的切削轨迹边缘起到了高度的增加，但是在磨削相对低速的情况下，砂轮磨粒的磨损会比较严重，导致磨粒脱落，以及工件的损伤也较大，因此会造成工件表面微观形貌粗糙度上升，而且外部的因素，如机床振动也会对工件磨削产生较大的激振效果，从而影响实验结果。

4 结论

1） 基于高斯正态分布与磨粒两两互不干涉原则对砂轮表面形貌进行仿真。通过单颗磨粒切削运动轨迹的研究和磨削热变形所产生的恢复形变以及耕犁效应的影响下，建立了单颗磨粒的三维轨迹数学方程，并根据区域优化和将最终将残余高度值拓扑映射至工件表面的模型设计原理，生成表面三维数值微观形貌模型。

2） 经过试验所得形貌与仿真结果的粗糙度数据对比，发现两者表面微观形貌特征基本一致。通过对不同的砂轮转速或不同的切削深度出发，了解了考虑磨削热变形下表面微观形貌生成的原理，并且可发现本次的理论建模的粗糙度误差最大可控制在13.31%，这不仅进一步说明了所建模型和求解的算法具有一定正确性与有效性，也从侧面说明了所提出的磨削热变形影响因素在磨削环境中具有一定可行性。

3） 该模型可以根据不同输入的加工工艺参数进行平面工件表面三维形貌的数值仿真，同时也可用于分析理论形貌的生成过程的研究及加工参数对结果的影响机理研究。