复杂曲面慢刀伺服加工刀具半径补偿算法
周玮,康敏 , ,郭航言
(1. 南京农业大学 工学院,南京 210031;2. 南京农业大学 江苏省智能农业装备重点实验室,南京 210031)
复杂光学曲面元件具有优异的光学性能,可实现由多个光学元件组合而成的复杂结构才具有的功能,有利于优化光学系统结构,进一步提高光学系统性能,在国防、航空航天等领域发挥着越来越重要的作用[1-4]。慢刀伺服车削技术可实现复杂光学曲面元件的重复加工,具有亚微米级或更高的面形精度、加工后无需处理可达纳米级表面粗糙度、加工效率高等优点,为高效率、高精度加工复杂光学曲面提供了一条新途径[5-7]。
刀具路径规划是实现复杂曲面慢刀伺服车削加工中的重要一环,直接决定着复杂曲面元件能否具有其特殊的光学性能。法向补偿算法较早应用于刀具补偿中,但法向补偿算法会在各运动轴上产生补偿分量,使各运动轴产生往复变速运动,慢刀伺服加工设备中X轴上质量元件较大,往复运动中换向瞬间会产生较大的跟踪误差,导致面形加工精度较低。为提高面形加工精度、满足机床动态性能,马富荣等[8]以正弦波面为例展开研究,提出了基于等距点的刀具半径补偿算法,使X轴的速度及加速度保持恒定;李佳伟等[9]指出法向刀具补偿算法在各运动轴上会产生附加运动量,导致某些运动轴速度或加速度产生突变,超出机床的动态响应能力,在此基础上提出了基于线段逼近刀具半径定向补偿的数值算法,保证了X轴单向匀速运动,提高了工件的加工精度;关朝亮等[10]对离轴抛物面加工的刀具补偿进行了研究,提出应将补偿量只加在机床负载较小的轴上,大幅度上减小了X轴的跟踪误差。上述研究均属于Z向补偿算法范畴,其实质是等距点先经插值算法拟合出等距曲线,再将刀触点x向坐标带入等距曲线获取近似刀位点,但所求刀位点精度与插值误差存在关联,目前关于方面的研究相对较少。
本文以慢刀伺服加工技术为背景,研究了法向补偿算法及Z向补偿算法的补偿原理;分析了待插点距插值节点的距离对插值误差及刀位点求解精度的影响;提出了基于弦长垂线的刀具补偿算法,并通过仿真、加工试验对该算法的可行性进行了验证,为高效率高精度的加工复杂曲面元件提供了一种新的刀具补偿方案。
1 慢刀伺服加工技术原理
慢刀伺服加工技术是一种超精密车削方法,可以高精度高效率地加工出复杂光学曲面,其加工机床典型布局形式与普通金刚石车床布局形式类似,包括X轴、Z轴两个直线轴和一个旋转轴C轴,慢刀伺服车削机床通过C、X、Z三轴联动带动金刚石刀具相对于工件端面在圆柱坐标系内实现螺旋形轨迹的切削运动,以实现对复杂曲面的加工[11]。图1所示为实验室自行研制的慢刀伺服数控机床结构示意 图。

图1 慢刀伺服数控机床结构示意图
2 刀具路径规划
慢刀伺服车削中,刀具刀刃与加工表面相切的点称为刀触点(Cutting contact point, CCP),由于复杂曲面各处曲率不同,因而实际切削时,刀触点可以是刀具刀刃上任意位置的点,因此需要在刀具上指定一固定点来确定刀具在切削过程中所处的位置,该点称为刀位点(Cutting location point, CLP)[12]。实际切削过程中,在曲面法线方向与Z轴方向处于非平行状态时,若刀位点由刀触点直接加上刀尖圆弧半径得到,刀具刀刃与曲面有可能形成过切区域,加工时会切除过多的材料,导致加工误差较大,难以满足曲面精度要求。慢刀伺服车削加工前需要根据曲面形状、刀具参数对刀具运动路径进行规划来求取正确的刀位点,以消除过切区域。刀具路径规划主要包括刀触点生成、刀具形状补偿、刀具轨迹插值等步骤[13],具体流程如图2 所示。

图2 刀具补偿流程图
2.1 刀触点轨迹规划
常用刀触点轨迹规划方法为等参数法、等截面法、等间距法和等残余高度法[13-14]。本文根据慢刀伺服加工中C轴为旋转轴,以及待加工工件多为回转体的特点,选取等截面法实现路径规划,以螺旋柱面为约束面[15-16]。慢刀伺服车削数控系统只能处理指定点间的运动,因此刀触点轨迹需要按照相应规则进行离散,刀触点轨迹离散常用方法为等角度离散和等弧长离散[17-19]。在慢刀伺服加工中,相邻数据点间运动时间ΔT恒定,等弧长离散会造成相邻数据点圆心角Δθ发生变化,如继续保证ΔT恒定,则C轴需变速进给,C轴因此产生加速度,慢刀伺服机床C轴为半闭环控制,故C轴会因加速而产生跟踪误差,降低了复杂曲面的加工质量。等角度离散法可实现C轴匀速运动,有效解决了等弧长离散存在的弊端。复杂光学曲面在实际加工中,刀具由工件边缘处切入,故等角度离散后刀触点轨迹为:
式中:ri为第i个刀触点到工件中心的距离;θi为初始刀触点与第i个刀触点间的夹角;Δθ为离散角;zi为第i个刀触点矢量高;af为X向每转进给量;D为工件直径。
2.2 传统刀具补偿算法
刀具补偿是为求解出正确的刀位点,补偿前需要确定刀具参数,一般刀具补偿所涉及的参数包括刀尖圆弧半径Rt、刀具后角αt、刀具前角λt,其中刀尖圆弧半径必须小于等于曲线的曲率半径,Rt≤1/K,K为曲线的最大曲率;刀具后角根据文献[20]所述方法做出选择,须保证刀具后角不与工件面形发生干涉;本文所选用前角λt为零。综上所述,刀具补偿仅需考虑切削平面上刀尖圆弧半径Rt的补偿,本文切削平面即为机床坐标系下的XZ平面。
2.2.1 法向补偿
刀具法向补偿模型如图3 所示,图3a)中,CC为工件与切削平面的截交线,截交线CC方程可由式(2)求出;CL为刀位点所在的曲线;n为刀触点P处曲面的法向矢量;np为法向矢量在切削平面上的投影;tp为刀触点P在截交线CC处的切向量;nz为平行于Z轴的向量。从图3b)可知,刀触点P的法向量np不一定平行于Z轴方向,若刀触点P直接Z向相加得到刀位点Lz1,可能会引起刀具过切,使刀具刀刃与待加工工件表面形成过切区域,导致复杂曲面元件面形精度较差,图3b)中黑色区域即Z向相加下所产生的过切区域。

图3 刀具圆弧半径补偿原理图
式中:f(x,y)为复杂曲面方程;θi为刀触点与工件圆心连线与X轴正向夹角。
法向补偿补偿算法可避免过切区域的产生,参照图3b),法向补偿算法具体操作步骤如下:
步骤1 按等角度离散法生成复杂曲面的离散刀触点,将生成的刀触点划分在nL条经过曲面中心的截交线CC上,nL= 360/Δθ;
步骤2 由曲线CC求解出P点处的切向量tp,再由几何关系np·tp= 0 求解出单位向量np;
步骤3 法向补偿下刀位点Lz2坐标为
从图3b)中可知,法向补偿算法优点在于所求刀位点精度较高,能有效消除过切区域,保证刀具刀刃与截交线CC相切与一点P,但法向补偿会在X向和Z向分别产生补偿分量Δx、Δz,但各刀触点处的法向量不同,补偿分量Δx、Δz也并非完全相同。补偿分量Δx会造成X轴做往复变速运动,而X轴工作台上负载质量较大,换向瞬间会产生较大的跟踪误差,不利于X向位置的精确控制。Z轴上负载质量较小,补偿分量Δz对Z轴的运动特性影响不明显,可以将补偿分量全部集中到Z轴上,以保证X轴可实现匀速运动。
2.2.2Z向补偿
Z向补偿是将补偿量全部集中到Z轴上,保证X轴实现匀速运动,以消除X轴换向时产生的跟踪误差,提高面形加工精度,参照(图3b)),Z向补偿算法具体操作步骤如下:
步骤1 按等角度离散法生成复杂曲面的离散刀触点,将生成的刀触点划分在nL条经过曲面中心的截交线CC上,nL= 360/Δθ;
步骤2 对同一条截交线CC上的刀触点进行法向补偿,求解出刀位点Lz2;
步骤3 利用所求刀位点Lz2,结合三次B 样条算法求解出等距线CL;
步骤4 将刀触点P的X向坐标xp带入等距曲线CL,即得到刀位点Lz3;
参照上述步骤,Z向补偿算法中,法向补偿所得刀位点即为插值节点,刀触点P的X向坐标xp即为待插点,各插值节点结合三次B 样条算法得到等距线CL,将待插点坐标带入等距曲线可求得近似刀位点坐标,但该算法所求刀位点精度受插值精度及待插点距插值节点的距离Lc共同影响。本文所用三次B 样条算法插值精度较高,故只要考虑Lc对计算结果精度的影响。
以sin(x)函数为例,探究Lc与插值误差之间的关系,具体操作如下:
步骤1 设定变量区间为0 ~ 90°,选取变量区间内的理论点作为插值节点,插值节点以0 为起始点,逐次增加10°;待插点以0 为起始点,逐次增加0.5°,要求插值节点、待插点在0 ~ 90°内;
步骤2 利用三次B 样条算法,拟合出插值节点函数方程法f(x);
步骤3 由式E(x) = |f(x) - sin(x)|求解出误差函数E(x),将待插点代入误差函数,求解出插值误差,误差变化趋势如图4 所示;
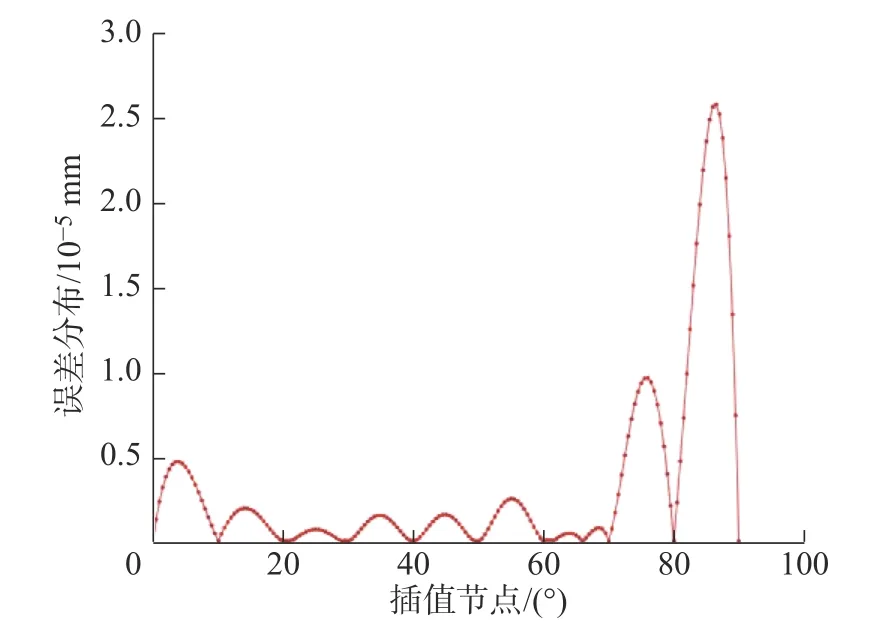
图4 Lc 与插值误差关系图
参照图4 可知,待插点距插值节点距离Lc越小,插值误差越小,插值精度越高。原因是:三次B 样条算法拟合精度较高,但该算法依靠数据点拟合曲线,拟合出的曲线本身便存在误差,而数据点本身为精确值,却不存在误差,所以越靠近给定数据点时误差越小,故在近似刀位点求取过程中,可通过减小Lc以提高近似刀位点的求解精度,提高面形加工精度。
2.3 弦长垂线刀具补偿算法
为进一步提高近似刀位点的求解精度,本文在上节研究的基础上提出一种基于弦长垂线的刀具补偿算法,该算法目的是较大程度上减小了Lc,求取高精度的近似刀位点坐标,提高复杂曲面面形的加工精度。参照图5,弦长垂线刀具补偿算法在柱坐标系下完成,具体操作步骤如下:

图5 弦长垂线刀具补偿原理图
步骤1 利用Z向相加算法求出点Lz1坐标,由于刀具半径小于截交线CC曲率半径,刀尖圆弧半径和截交线的交点除点P外,还有一点P′,根据式(4)求出P′坐标,即:
式中:(X0,Z0)为Lz1点的坐标;z=f(ρcosθ,ρsinθ)为柱坐标下截交线CC方程。
步骤2 求出直线PP′的斜率,由于PP′ ⊥Lz1C,由KPP′·KLz1C =-1,求出直线Lz1C的斜率,进而求出直线Lz1C的直线方程,根据式(5)求出C点坐标,即:
步骤3 根据式(6)求出E点坐标,即:
步骤4 点Lz1沿CE向量移动,移动距离为CE的长度,进而求得插值节点Lz4;
步骤5 利用所求插值节点Lz4,结合分段三次样条插值算法求解出等距线CL;
步骤6 将刀触点P的X向坐标xp代入等距曲线CL,即得到刀位点Lz5;
与法向补偿相比,弦长垂线刀具补偿算法避免了X向产生补偿分量Δx,保证了X轴单向匀速运动,消除了因法向补偿后X轴做往复变速运动所产生的跟踪误差;与Z向补偿相比,在保证等距曲线CL精度的前提下,弦长垂线补偿算法目的是减小待插点距插值节点的距离,以提高近似刀位点求解精度。
3 刀具路径规划仿真及试验分析
3.1 等角度及等弧长离散误差仿真
以离散弧长Δl= 1 mm,离散角Δθ= 3°为参数生成离散刀触点,将两种离散法生成的刀触点Z值进行分段三次样条插值,将插值点与理论点相减获取离散误差。如图6 所示,等角度离散法靠近圆心处离散误差较小,外侧离散误差较大;等弧长离散法靠近圆心处离散误差较大,外侧离散误差较小,从整体误差分布看等角度离散法的离散误差较小。本文所加工环曲面被广泛应用于眼镜片制作领域中,要求环曲面圆心处具有较高的面形精度,故本文采用等角度法获取离散刀触点。

图6 刀触点生成算法离散误差
3.2 刀具路径规划仿真
以环曲面为例进行仿真分析,仿真内容为:1)环曲面理论面形及刀触点轨迹;2)弦长垂线刀具补偿算法及法向补偿算法下X轴的运动特性;3)弦长垂线刀具补偿算法及Z向补偿算法下Lc的变化范围;4)弦长垂线刀具补偿算法及Z向补偿算法下环曲面面形加工精度仿真;5)弦长垂线刀具补偿算法下环曲面刀位点、刀触点轨迹仿真、刀具补偿量分布图。通过上述仿真分析以验证弦长垂线刀具补偿算法下慢刀伺服车削加工的可行性。常被应用于散光矫正中[21],环曲面是由半径为a的基弧,绕同一平面内但不通过基弧圆心的轴线以半径为R旋转得到的圆环形表面,如图7 所示,正交弧半径R> 基弧半径a,图7a)上的圆圈区域表面即为图7b)中的环曲面眼镜片面型。

图7 环曲面三维示意图
环曲面在笛卡尔坐标系下的方程为
本文仿真软件为MATLAB,仿真参数如表1 所示。图8 为环曲面理论面形及刀触点轨迹,可以看出等角度离散法下的刀触点轨迹与理论面形保持一致,在此基础上可继续研究刀位点生成算法。

表1 仿真参数表
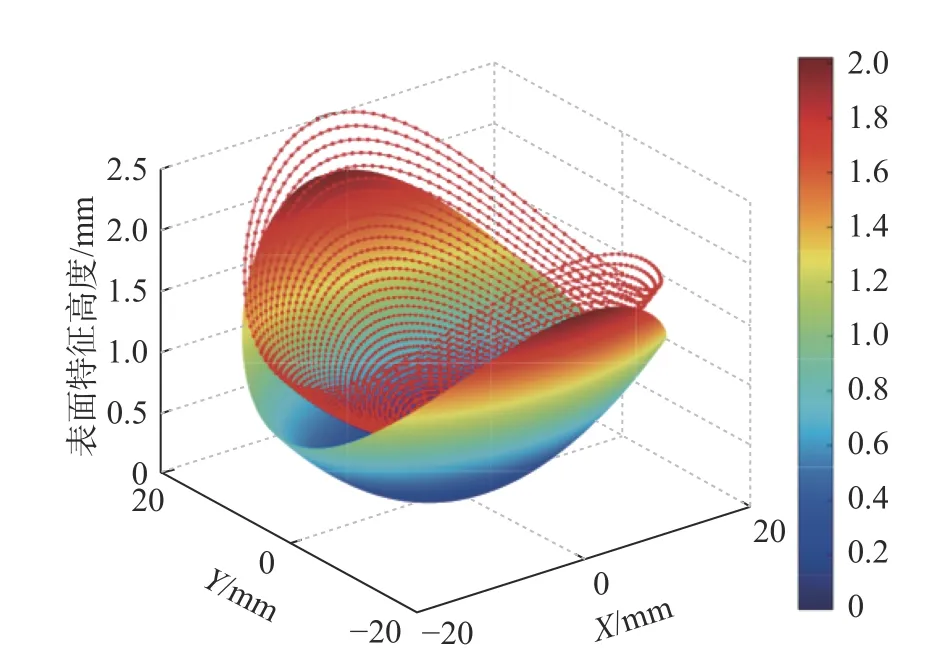
图8 环曲面理论面形及刀触点轨迹分布
进一步分析不同算法下X轴的运动特性,由于Z向补偿与弦长垂线刀具补偿算法的原理相同,对X轴运动特性的影响也相同,故本文只探讨弦长垂线刀具补偿算法及法向补偿算法对X轴运动特性的影响。图9a) ~ 图9f)分别为法向补偿算法及弦长垂线刀具补偿算法下X轴运动特性图,从图9a)、图9c)、图9e)中可知,法向补偿算法下X轴运动轨迹会有小幅度的往复偏摆运动,造成X轴做往复变速运动,使X轴产生较大的加速度,导致X轴剧烈运动,增大了跟踪误差,影响最终面形加工精度;从图9b)、图9d)、图9f)中可知,弦长垂线刀具补偿算法下X轴运动轨迹为一条斜线,X轴速度及加速度保持恒指,保证了X轴向工作台运动平稳,消除了X轴往复运动所产生的跟踪误差,有利于提高面形加工精度。

图9 等参数下两种算法下Lc 分布范围
上文中以sin(x)为例探究了待插点距插值节点的距离Lc对插值误差的影响,研究表明Lc越小,插值精度越高。Z向补偿算法和弦长垂线补偿算法可解决法向补偿算法中存在的问题,但都需将待插点带入由插值点经三次B 样条插值算法拟合的曲线才可以获取最终刀位点,Lc与面形加工精度会存在一定联系。图10 为两种补偿算法Lc的分布范围,其中Z向补偿算法Lc峰值为9.94 × 10-2mm,弦长垂线刀具补偿算法下Lc峰值为7.52 × 10-4mm,结果表明弦长垂线刀具补偿算法下Lc峰值要远小于Z向补偿算法下Lc峰值;从整体分布范围看,同一位置处弦长垂线刀具补偿算法下Lc也小于Z向补偿算法下Lc,参照上述分析可知弦长垂线刀具补偿算法下的插值误差要小于Z向补偿算法,进而从理论上得出弦长垂线刀具补偿算法下面形加工精度要优于Z向补偿算法。

图10 等参数下两种算法下Lc 分布范围
进一步对Z向补偿算法及弦长垂线刀具补偿算法下面形加工精度仿真,仿真前需将表1 中的每圈进给量af调整为0.01 mm,仿真结果如图11 所示。从图11 中可知,Z向补偿算法下面形误差PV值为6.2 μm,弦长垂线刀具补偿算法下面形误差PV值为2.2 μm,对比可知弦长垂线刀具补偿算法面形加工仿真精度要优于Z向补偿算法,主要原因是弦长垂线刀具补偿算法下待插点距插值节点距离Lc要小于Z向补偿算法下的Lc,造成弦长垂线刀具补偿算法下插值误差要小于Z向补偿,保证了弦长垂线刀具补偿算法下的面形加工精度较高。由图10 可知,Z向补偿算法及弦长垂线补偿算法下的面形加工仿真精度均是靠近圆心处的精度高于外侧精度,原因在于等角度离散法下靠近曲面中心处离散误差较小,造成了靠近中心处的加工质量要高于边缘处。
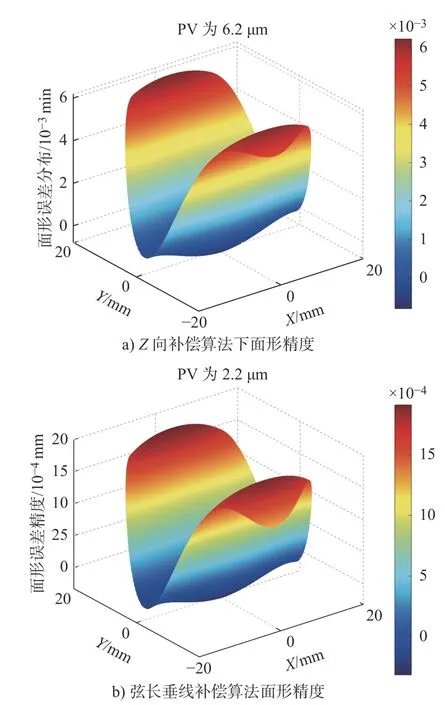
图11 等参数下两种算法下面形精度
理论和仿真分析表明,弦长垂线刀具补偿算法下X轴运动特性要优于法向补偿算法;与Z向补偿算法相比,弦长垂线刀具补偿算法下Lc较小,表面弦长垂线补偿算法下的插值误差较小;弦长垂线刀具补偿算法下面形仿真精度优于Z向补偿算法,满足曲面加工精度要求,故本文选用弦长垂线刀具补偿算法求解环曲面刀位点,用以完成环曲面加工。
图12为弦长垂线刀具补偿算法下环曲面刀具运动路径仿真,相关仿真参数如表1 所示。从图12a)、图12b)中可知弦长垂线刀具补偿算法下所得刀位点路径、分布状态与刀触点保持一致,满足加工要求;图12c)为环曲面刀具形状补偿量分布图,从图中可知弦长垂线刀具补偿算法下刀具补偿量在合理补偿范围内,无过大或过小跳变补偿,保证了Z轴平稳运动,满足加工要求;图12d)为Z轴加工中最外两圈速度运动图,从图中可知Z轴运动平稳,无速度剧烈变化等问题,满足Z轴运动特性要求。综合分析,弦长垂线刀具补偿算法所生成的数控加工代码符合慢刀伺服车床各轴运动特性要求,可应用于实际车削加工。
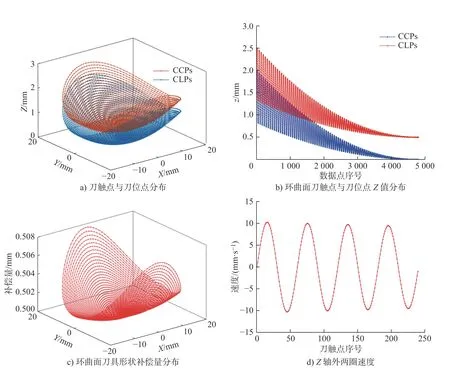
图12 环曲面刀具路径仿真
3.3 环曲面加工试验
利用实验室自主研制的慢刀伺服数控机床进行环曲面的加工,如图13 所示,实现曲面数控加工的算法为:Z向补偿算法、弦长垂线补偿算法;工件材料为PMMA(聚甲基丙烯酸甲酯),所用刀具圆弧半径Rt= 0.5 mm,每圈进给量af= 0.01 mm/r,切屑深度ap= 0.01 mm,其余参数与上述仿真参数相同。

图13 复杂曲面实际加工示意图
3.4 试验结果分析
目前常以复杂曲面面形精度及表面粗糙度作为刀具补偿算法性能评价指标[22]。本文使用MQ696型三坐标测量仪以圆周式测量方法测量加工所得环曲面面形数据,所用三坐标测量机技术性能参数如表2 所示。利用相关数据匹配算法实现测量数据与理论数据的匹配,获取加工表面面形精度[23-24]。

表2 三坐标测量机设备参数表
图14a)为Z向补偿算法下面形误差分布,PV值为0.017 mm,图14b)为弦长垂线补偿算法面形误差分布,PV 值为0.008 mm,可知弦长垂线补偿算法下所加工表面误差分布与仿真图保持一致,有利于后期面形修正,而Z向补偿算法下面形误差分布散乱,面形修正难度较大,且弦长垂线刀具补偿算法面形加工精度要优于Z向补偿算法。采用JB-4C 型接触式表面粗糙度测量仪对工件表面粗糙度进行测量,按等角度测量表面8 处粗糙度,如图15 所示,最后求取平均值作为表面粗糙度值。弦长垂线刀具补偿算法下表面粗糙度为49.2 nm,Z向补偿算法表面粗糙为49.5 nm,两组算法下表面粗糙度变化不明显,表明同等参数下刀具补偿算法对表面粗糙度影响不大。

图14 两种算法下面形精度图

图15 弦长垂线补偿算法下环曲面表面粗糙度
4 结论
1)法向补偿算法会在X向产生补偿分量,造成X轴处速度及加速度变化剧烈,不利于运动惯量较大的X向工作台的精确控制,影响最终面形加工精度;证明了插值点距待插点的距离Lc越小,插值精度越高,Lc影响着近似刀位点的求解精度。
2)与法向补偿算法相比,弦长垂线补偿算法下X轴运动平稳,速度及加速度保持恒定,有利于X向工作台的精确控制;弦长垂线补偿算法下近似刀位点求解精度及面形加工仿真精度均优于Z向补偿算法。仿真结果表明弦长垂线补偿算法可进一步提升复杂曲面元件的面形加工精度。
3)使用MATLAB 软件对环曲面进行刀具路径规划仿真,并通过试验进行验证,试验结果表明弦长垂线刀具补偿算法下面形精度较高,证明了该算法可有效提升复杂曲面元件的面形加工精度,可应用于实际生产制造中。

