准确把握契机，巧妙渗透数学思想

程晨

［摘  要］ 尽管数学思想在教材或课堂中没有具体的教学内容，但其应蕴含于教师的教学过程之中，蕴含于学生的数学思维之中。文章以“长方形和正方形”的复习课为例，论述渗透数学思想方法的策略。

［关键词］ 数学思想方法；长方形；正方形；数学思维

一、提出问题

“让学生获得适应未来发展所必须的基本的数学思想方法”是新课程标准的目标之一。数学思想是数学之灵魂，对学生而言，最有用的并非是数学知识，而是数学的思想方法。基于此，在新课程实施的今天，教师应更新教学观念，在思想上和观念上都应提升对渗透数学思想方法的认识，并将其纳入教学目标，在各种课型的各个环节中时时渗透。因此，教师需要尽最大努力探寻渗透数学思想方法的契机，为学生形成较强的发现、提出、分析和解决问题的能力奠基，从而发展学生的思维能力和创新能力。本文以“长方形和正方形”的复习课为例，结合实践案例谈一点渗透数学思想方法的体会。

二、教学过程

片段1：复习梳理，温故而知新

师：大家请看，这张纸是什么形状的？（教师高举一张长方形纸片）

生（齐）：长方形。

师：哪位同学能说一说长方形有哪些主要特征？

生1：有四条边，且对边相等。

生2：有四个角，且都是直角。（课件出示一个长方形，并根据学生的阐述列举特征）

师：谁还知道哪些与长方形有关的特征？

生3：长方形四条边中的两条长边的长叫作长，两条短边的长叫作宽。

师：这又是什么图形？……（出示一个正方形纸片，并引导学生一一说出正方形的特征）

师：谁来说一说它们的周长分别怎么求？

生3：长方形的周长＝（长＋宽）×2。

生4：正方形的周长＝边长×4。

师：请试着口算出这个长是10厘米、宽是5厘米的长方形的周 长。

生5：10+5=15（厘米），15×2=30（厘米）。

师：很好，谁能算出这个边长是8厘米的正方形的周长？

生6：8×4=32（厘米）。

师：不错，虽然今天是一节复习课，但老师想通过“玩”的方式带着你们一起长知识、长智慧。

评析：温故而知新，通过感知实物，让学生积极主动回忆旧知，熟悉长方形和正方形的特征及周长的计算方法，进而为接下来探究活动的开展打下基础。

片段2：拼法比拼，渗透对比思想

师：先让我们来玩长方形，大家看，这里有两张长10厘米、宽5厘米的长方形纸片， 试着拼一拼，可以拼成什么图形？（学生动手操作，很快有了成果）

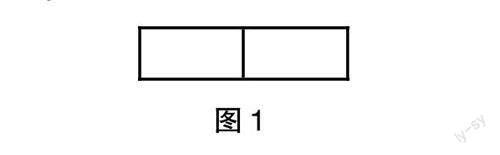
生7：如图1，可以拼成一个大长方形。

师：谁能算出这个大长方形的周长？（大家积极投入计算）

生8：我是先算出它的長为10×2=20（厘米），再算出一条长加一条宽的和为20+5=25（厘米），最后得出周长25×2=50（厘米）。

生9：我还有其他方法……

师：还有其他拼法吗？

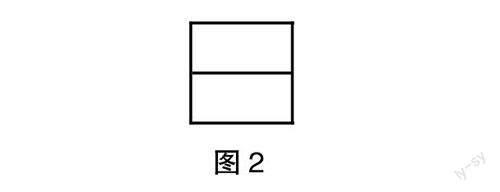
生9：如图2，可以拼成一个正方形。

师：那这个正方形的周长该如何求？

生9：先算出边长为5×2=10（厘米），再算出周长为10×4=40（厘米）。

师：那么，拼成的两个图形的周长一样吗？

生：不一样。

师：为什么不一样呢？

生10：拼长方形的时候是将小长方形的宽拼在一起的，而拼正方形的时候是将长拼在一起的。

师：换句话说，两种不同的拼法“消失”的不同，各是什么？

生10：拼长方形时消失的是两条宽，拼正方形时消失的是两条长。

师：哇，真是观察仔细的好孩子！长和宽的长度不同，所以拼成图形的周长不相同。

评析：拼图是小学生擅长的，本环节中教师引导学生去操作、观察和比较，让学生在对比中发现“不同的拼法，拼成的图形周长不一样”。就这样，让学生卷入数学观察和数学思考中去，从而使思维向着纵深发展。同时，通过对比思考的过程，教师水到渠成地渗透了对比思想。

片段3：步步深入，渗透转化思想

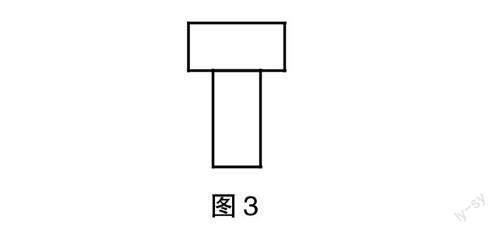
师：刚才我们“玩”的难度较小，是老师轻敌了！下面，我们来玩个难度大的。如图3，将这两个长方形拼成这样一个T字图形，它的周长又是多少？（学生跃跃欲试，思考、计算一气呵成，教师巡视）

师：大家的方法都非常有创意，谁愿意先来展示？

生11：我用的是数边法。先找出10厘米长的边，共3条，即10×3=30（厘米）；再找出5厘米长的边，共4条，即5×4=20厘米；最后相加得出周长为30+20=50（厘米）。

生12：我用的是减边法。先算出两个小长方形的周长和，即10+5=15（厘米），15×2=30（厘米），30×2=60（厘米）；再减去“消失”的2条宽，即5×2=10（厘米）；最后相减得出周长为60-10=50（厘米）。

生13：我用的是变形法，就是一番操作后将图3变形成图4所示的大长方形，它的长是10+5=15（厘米），宽是10厘米，周长为15+10=25（厘米），25×2=50（厘米）。

师：哇，真是个爱动脑筋的好孩子！这样一变，原来的图形就成了一个长方形，图形变大了，周长变化了吗？

生（齐）：没有。

师：以上三种方法，哪一种最巧妙？

生（齐）：最后一种。

评析：在课本中，对一些不规则图形的呈现往往都赋予了方格纸这样的背景，如此一来，学生就很容易想到了转化的方法。但没有了这样的背景，学生很难想到通过平移变形的方法解决问题。以上环节中，教师通过设问“探求T字图形的周长”，让学生在思考和探究之后想到多种解决问题的方法，其中“数边法”具有直观性，只需根据边的长度分别数出即可；“减边法”不易想到，却是常用解决问题的方法；“变形法”具有创造性，想法巧妙，充分彰显了转化的数学思想。

师：如果将两个长方形拼成图5所示的图形，它的周长该如何求呢？（学生投入思考中，并在上述解法的启发下，很快有了思路）

生14：可以用“变形法”将其变成一个大长方形，这个大长方形的长15厘米，宽10厘米，15+10=25（厘米），则周长为25×2=50（厘米）。

师：那刚才的两个图形周长相同吗？（课件同时呈现两个图形）

生（齐）：相同，两个都是50厘米。

师：为什么它们的形状不同，而周长却相同呢？

生15：因为它们都可以变形成相同的大长方形。

师：非常好，刚才两个图形都是通过平移线段的方法进行变形，得出了相同的大长方形，这种方法就是“转化”。经过转化，大长方形与之前的小长方形有何关系？（同时课件出示问题，学生在观察、思考和讨论后，很快给出答案）

师：借助这两个长方形，你还能拼成多少个周长是50厘米的图形？

……

评析：以上环节中，教师通过探究性问题引导学生观察和思考，让学生在探索中逐步感悟转化的思想方法。当学生认识到上述两种图形都可以变成同一个长方形時，转化思想已经初见端倪。此时，教师适时揭示主旨，并及时追问，让学生领悟到转化前后图形间的关联，进而深化认识，同时将转化的思想方法扎根于学生的思想深处。

三、教学思考

新课程理念下，教师设计合理而有效的探究活动，摆脱以往复习课教学的循环往复的练习，根据学生的已有知识经验，引领学生参与实践操作和思维探究活动，在体验活动的过程中自然而然地渗透数学思想方法，以提升学生的学习力。

本课中，教师选取的活动素材合理，便于学生按照自己的探究进行数学活动，自然地引发数学思考，为数学思想方法的形成奠定了良好的基础。进一步地，整个探究活动的过程中，教师准确激活学生的原有知识、经验和思维，使其在观察、对比和思考中完成知识和方法的自主建构，实现数学思想方法的自然融合。最重要的是，每个环节中都增设了总结提炼，它可以深化、精练和概括知识，可以为学生能力的发展和提高提供机会，可以为数学思想的渗透提供助力，可以为数学学科关键性能力的发展添砖加瓦。

总之，数学课堂教学必须重视数学思想方法的挖掘、研究和渗透，以适应新课改的需要。当然，数学思想方法的渗透并非一蹴而就的，需要教师一以贯之地加以引导，让学生经历螺旋上升的过程，使学生的认识更加深刻，从而使学生对数学的理解实现质的飞跃。