活用物理结论避免固化思维
罗金龙


摘 要:推导出连接体问题中的内力公式,并说明其适用条件,再以2022届湖北十一校第二次联考物理第7题为例,阐述了该题与经典模型的区别与联系。最后将内力公式及其涉及的模型拓展,并探究该模型拓展后可能出现的设问方式,进而让学生意识到活用物理结论的重要性。
关键词:连接体;内力公式;物理模型;学习思维
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2023)5-0042-3
自2021年起,全国有多个省份作为“第三批新高考试点省份”推行了新的高考模式,在新高考改革方案下,物理作為选考科目,均是各省份自主命题,在这一大趋势下,就物理这一学科而言,各省试题难度、题型、风格各异,也就催生了不少新题型。细细分析,这类题型既有一些经典物理模型与结论的影子,却又有别于经典模型与结论。如果学生遇到这类题时,仅凭已掌握的知识和主观意识进行判断,而不对其内在原理加以分析,往往就会作出错误的判断。针对这一情况,笔者以2022届湖北十一校第二次联考物理第7题为例,分析了此题的创新情境与经典物理结论“连接体问题中的内力公式”的区别与联系,并详细阐述了该模型的创新变化及可能出现的设题方式。希望学生能对该模型有更深刻的认识,并从中体会到避免学习思维固化的重要性。
1 连接体问题内力公式的结论推导及适用条件
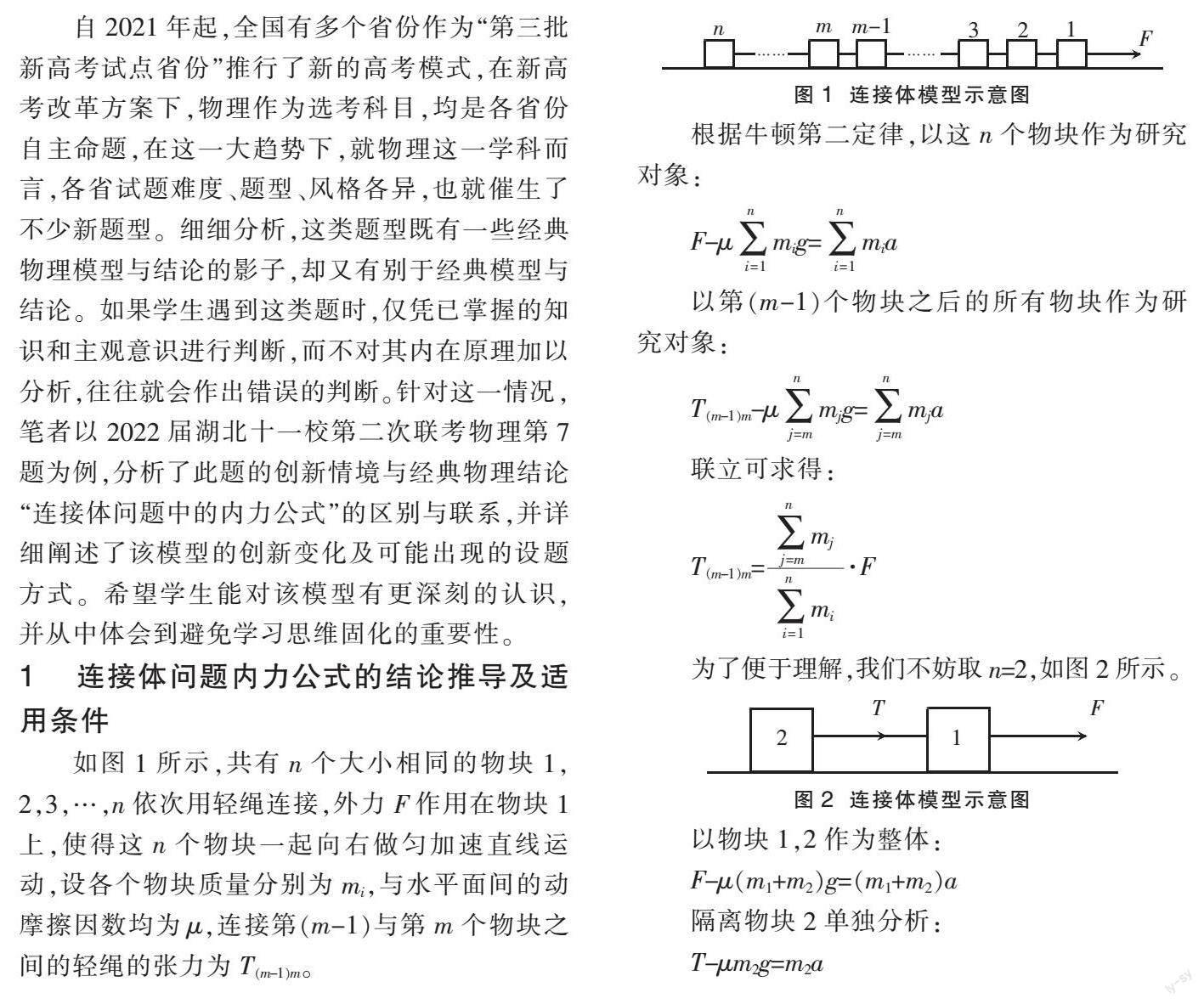
如图1所示,共有n个大小相同的物块1,
2,3,…,n依次用轻绳连接,外力F作用在物块1上,使得这n个物块一起向右做匀加速直线运动,设各个物块质量分别为mi,与水平面间的动摩擦因数均为μ,连接第(m-1)与第m个物块之间的轻绳的张力为T(m-1)m。
从(2)式可以看出,细线张力T等于物块2的质量与两物块总质量之比和外力F的乘积,这就是连接体问题中的内力公式。
值得注意的是,地面光滑即μ=0也是动摩擦因数相同的一种特殊情况,此情况下所得结论将与(2)式相同,此处不再加以推导。实际上,这一结论不仅可用于水平地面,在斜面上、竖直方向上均可使用。
仔细观察上述推导过程不难发现,我们是基于各物块与水平面间的动摩擦因数相同这一条件才得出结论。值得思考的是,当两物块与水平面间的动摩擦因数不同时,(2)式是否仍然成立?接下来进行推导。
显然,当动摩擦因数不同时,(2)式将不再成立。到此,我们知道,在运用连接体内力公式时,要仔细看清题给条件是否满足“各物块与水平面间的动摩擦因数相同”。
2 原题再现
在完成相关结论的推导及适用条件的探究后,对湖北十一校第二次联考物理第7题进行分析,原题如下:
如图3、图4所示,A,B两木块放在粗糙水平面上,它们之间用不可伸长的轻绳相连,两次连接情况中轻绳倾斜方向不同,已知两木块与水平面间的动摩擦因数分别为μA和μB,且0<μA<μB,先后用水平拉力F1和F2拉着A,B一起水平向右匀速运动,则匀速运动过程中( )
题目分析:虽然本题研究的是匀速运动过程,但我们知道匀速直线运动是匀加速直线运动的一种特殊情况。而该题与“连接体问题内力公式”所涉及的模型的最大差别在于连接两木块之间的细线是倾斜的,且两木块与水平面间的动摩擦因数并不相同,虽然本题并未提及细线张力的大小,但是显然本题不能运用内力公式进行处理和作相关判断,而要对各物体的受力情况加以分析后才能作出准确判断。
解析 设在第一种情况中细线张力在水平方向的分力为Tx1,在竖直方向的分力为Ty1,第二种情况细线张力在水平方向和竖直方向的分力分别为Tx2,Ty2。
本题总结:
从上述解题过程可知,前后两种情况F1,F2并不相等,且F1,F2的大小关系与动摩擦因数有关。不难看出,当μA=μB时,F1=F2,而细线倾斜对本题的判断并无影响。前文提到,匀速直线运动仅为匀加速直线运动的一种特殊情况,显然当我们将本题前后两种情况的运动状态改为做加速度相同的匀加速直线运动时,(3)式变为F1=μBmBg+μAmAg+Ty1(μB-μA)+(mA+mB)a,(4)式变为F2=μBmBg+μAmAg+Ty2(μA-μB)+(mA+mB)a,此时仍有F1>F2。
本题的易错点在于我们可能直接将两木块视作一个整体,而忽略了动摩擦因数不同这一条件,从而得出F1=F2这一误判。故我们得到启示:当在判断与已有模型及相关结论类似的题目内容时,一定要仔细分析题目是否符合相关结论的适用条件,应避免学习思维固化从而犯下主观臆断的错误。
值得注意的是,本题仅考查了在匀速运动的前提下前后两种情况外力的大小关系,并未对连接两木块之间的倾斜轻绳进行深入分析,为此,我们可适当改变题给条件,进一步探究倾斜轻绳中张力的大小。
3 模型拓展
若细线倾斜方向与图4相同,显然所得结论与上述类似,感兴趣的老师可自行推导。
4 结束语
在学习高中物理的过程中,要学会分辨物理模型及结论是否适用于具体题目,应避免“硬套结论,学习思维固化”这一不良现象。同时,我们应养成自主探究、发现问题的学习习惯,对于已有的物理模型及结论要尝试自主分析其可能出现的创新情境,并能够找出创新情境与原有模型的区别与联系,如“特殊与一般”的关系,适用条件是否发生改变等,进而做到对物理模型的拓展与迁移。如此,既能让我们对物理这门学科产生更深刻的认识,又能提升我们思考问题的能力和培养良好的思维习惯。
(栏目编辑 陈 洁)
物理教学探讨2023年5期
