三新背景下高中物理实验生活化实践
陈云富 张津搏


摘 要:新高考、新课程、新教材强调学生构建物理模型来解决实际问题。在步行、自驾游和动车出行三种生活情境下,利用智能手机Phyphox软件的定位功能获取高精度的经纬度数据和两点间的最短距离数据,分别以球面直角三角形的斜边、两点直线距离、最大圆的弧长表示球面两点的最短距离,构建三种模型来估算地球半径。在最短距离不超过三百公里时,三种模型得到的地球半径相对误差小、不确定度小。在实际运用中,用三种模型计算了浙江温州与多个城市之间的距离,得出三种模型的使用条件及系统误差的规律。
关键词:三新背景;地球半径;经纬度;Phyphox
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2023)5-0052-5
1 问题背景及模型建构
中学物理教学受学科本位和知识本位的影响,与学生生活和社会实际联系不够紧密,难以培养学生构建物理模型来解决实际问题的能力,难以提高学生学习物理的兴趣。研究高中物理实验生活化,符合新高考、新课程、新教材“把学习当作是人发展的一部分”的全新理念,是一个具有现实意义的课题[1]。
人教版高中物理必修第二册第七章第三节“万有引力理论的成就”称量地球的质量、第四节“宇宙航行”计算第一宇宙速度,均用到一个重要的物理常量——地球半径。查阅资料可知,地球是个两极稍扁、赤道略鼓的扁球体,能近似看作一个球体。从公元前300年左右的埃拉托色尼测量地球周长的实验开始[2],人类在测量地球半径的道路上经历了漫长的旅程。随着测量技术不断发展,测量精度不断提高,当前公认的地心到两极的距离为6 356.908 8 km,地心到赤道的距离为6 377.830 0 km,地心到地表各点距离的平均值为6 371.393 0 km。本文利用手机定位功能获取经纬度数据和两点间的最短距离数据,建立合适的物理模型计算地球半径[3-4],从而让学生更好地认识物理世界,培养物理学科素养。
1.1 以球面直角三角形的斜边表示球面两点最短距离
经度是地球上一个地点离一根被称为本初子午线的南北方向走线以东或以西的度数。在本初子午线以东的经度叫东经,用E表示;在本初子午线以西的经度叫西经,用W表示。纬度是指地球上某点与地球球心的连线和地球赤道面所成的线面角,其数值在0°至90°之间。位于赤道以北的点的纬度叫北纬,记为N;位于赤道以南的点的纬度叫南纬,记为S。手机定位(GPS)功能可以提供两个点A和B间的直线距离LAB以及两点的经度和纬度,分别记为(φA,δA)和(φB,δB),其中φA,δA,φB,δB均以弧度制表示。
2 实验操作和数据分析
智能手机上有加速度传感器、声传感器、光传感器、霍尔传感器及角速度传感器等多种灵敏传感器。本文在步行、自驾游和动车出行三种生活情境下,利用智能手机Phyphox软件的定位功能获取数据,由构建的三种模型估算地球半径,并比较三种方法的优劣。
图3左侧为软件Phyphox的主界面,我们选择点击①处的“定位(GPS)”功能进入到图3右侧所示的界面,选择②位置处的“简明值”功能,即可测量当前位置的经纬度和距离,从③位置处记录经纬度数据能显示到小数点后6位,文件导出可以保留10位有效数字。图3中④位置處的“已行驶距离”表示从起点开始走过的路程,“距起点距离”表示该位置与起点之间的最小距离。
2.1 直线步道:步行沿滨海新区休闲景观绿道
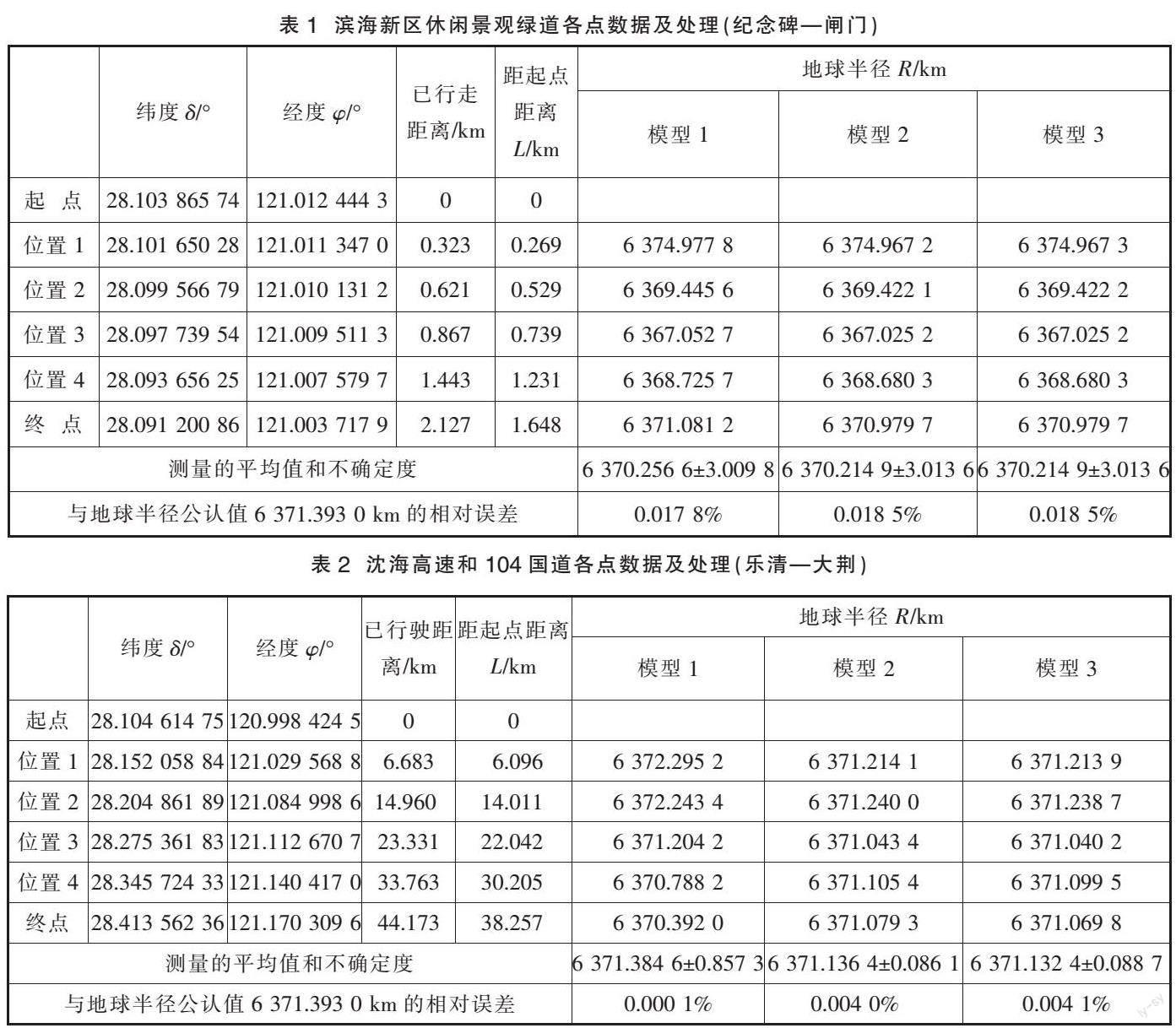
从乐清抗台救灾纪念碑开始打开软件,沿滨海新区休闲景观绿道步行,每走几百米,遇见绿道旁长椅坐下,将手机静置于长椅上至各数据不再变化时截图。抵达胜利塘闸门附近关闭软件,全程历时27 min,距起点最远距离为1.648 km,最大路程为2.127 km。将全过程数据以Excel表格的形式发送至手机保存。根据截图纬度数据在Excel表格中查找10位有效数字的经纬度信息,连同已行走距离和距起点距离填入表1。
测量过程中,全程中间4个位置在图4中标出,为途中长椅所在位置。令起点为A点,位置i(i=1,2,3,4)和终点为B点,数据代入(4)(7)和(10)式,可分别计算三种模型下的地球半径,将5次求得的地球半径取平均值,计算不确定度,并与地球半径公认值6 371.393 0 km比较,求出平均值和公认值的相对误差。三种模型的计算结果相对误差都比较小,不确定度在3 km左右。
2.2 崎岖公路:自驾游沿沈海高速和104国道
从乐清人才公寓红绿灯处出发,打开软件,通过沈海高速和104国道前往大荆铁定溜溜游乐园。笔者全程坐在副驾驶座上观察软件已行驶的距离,每隔6~10公里直接截图保存,全程历时39 min左右,距起点最远距离为38.257 km,最大路程为44.173 km,将全过程数据以Excel表格的形式发送至手机保存,查找有关数据填入表2中。
测量过程中,全程中间4个位置在图5中标出。用相同的方式获取并记录数据,手机定位数据存在延后,但对于远距离行驶的车辆而言,其造成的影响可以忽略。由于运动距离的增加,测量不确定度与步行相比明显减小,相对误差也有所减小。三种模型的计算结果相对误差都非常小,不确定度在0.08 km~0.8 km。
2.3 弧形轨道:动车从杭州东到乐清东铁路
乘坐G7575次列车从杭州东站出发,沿途停靠绍兴北、嵊州新昌、天台山、临海、台州和温岭站点,抵达乐清东站。笔者坐在靠窗位置,每经过一个站点,将手机静置于窗台上,待手机经纬度数据不再变化时,截屏保存图像。抵达乐清东站时关闭软件,全程经历2小时9分钟,距起点最远距离为244.723 km,最大路程为321.736 km,将全过程数据以Excel表格的形式发送至手机保存,查找有关数据填入表3中。
测量过程中,中间6个站点位置在图6中标出。用相同的方式获取数据并记录数据至表3,模型1测量不确定度和相对误差较自驾游有所增加,说明该模型在两百千米时,误差会逐渐增大。模型2和模型3的计算结果与自驾游基本持平,优于步行结果。模型2和模型3的测量结果相对误差都非常小,不确定度在0.7 km~0.8 km。
综上所述,(4)式得出时,△AA2B不在平面上,而是在地球的球面上,视为平面直角三角形并使用勾股定理会存在系统误差。将地球看成是球体,在步行、自驾游和动车出行三种情境下,走直线步道、崎岖公路和弧形动车轨道,均能获得比较理想的测量不确定度和相对误差,三种模型求解地球半径都是可行的,结果也是可靠的。
3 实验验证和应用
笔者将在更大的尺度上,讨论三种模型的适用情况。以浙江温州为起点,在百度地图中测量其与北京、拉萨、孟买、迪拜、基辅、雅典和巴黎的距离,如图7所示。测量时先在较小的比例尺下选择温州,再输入目标城市查询,在合适的比例尺下确定终点,位置不对还可以进行微调。打开经纬度查询定位网站(网址:http://jingweidu.757dy.com/),查找上述八座城市的经纬度数据,将网站查询数据和百度地图测量数据一同填入表4中。由公式(11)(12)(13)计算两地距离,所有计算结果填入表4中。
使用模型1时,若两地距离近,计算相对误差小,如北京;若两地纬度接近,计算相对误差小,如迪拜;若两地距离远,纬度、经度跨越均大,计算相对误差大,计算值明显大于测量值,如基辅、巴黎。模型1适用条件:①两地距离近;②两地纬度接近;③两地经度接近。使用模型2时,相对误差随两地距离的增加而增加,计算值小于测量值。使用模型3时,两地距离计算值和测量值均接近,满足各种条件下计算两地距离,拉萨的相对误差略大,猜测与其高海拔有关。
4 反思與改进
模型1、模型2、模型3在短距离情况下计算地球半径,测量的不确定度小,相对误差也小。当两地距离大时,使用模型3计算结果可靠。本文没有考虑海拔对两地距离计算的影响,可以预见:在经纬度差异很小的悬崖处,在飞机飞行过程中不考虑飞机高度变化等情境下,模型3的计算结果偏差也会变大。
高中物理实验生活化是对实验室专门化实验的丰富延伸和有益补充,它贯穿于课堂内外,具有浓郁的生活气息,以时时可参与、人人可体验的“深度的可体验性”特征。通过合理规划与统筹安排,让生活化创新物理实验在促进学生形成物理观念、提升科学思维能力、增强科学探究能力、养成科学态度与责任方面充分发挥其特色优势。
参考文献:
[1]付鸿.新课程标准下高中物理教学生活化研究与实践[D].哈尔滨:哈尔滨师范大学,2015.
[2]宫铁波,张炳恒. 十大经典物理实验回顾[J]. 大学物理实验,2003,16(2):80-83.
[3]张愉,张雄.用iPhone5s的摄像机巧测地球半径的方法[J].物理教学探讨,2015,33(3):54-55,60.
[4]刘智谦.使用手机GPS定位软件巧测地球半径[J].实验教学与仪器,2018,35(1):71-72.
(栏目编辑 刘 荣)

