光路可逆原理错了吗？

2023-05-30 00:11焦芳枝邹愉

物理教学探讨 2023年5期

焦芳枝邹愉

摘要：光路可逆原理是几何光学中的重要内容，但有时利用光路可逆原理分析问题却可能出现不自洽的情境。通过一个具体实例引入半波损失的概念，对光波的相位进行分析，用波动光学成功解释了几何光学中的一个佯谬，体现了几何光学和波动光学的紧密联系，培养了学生多角度看待问题的科学思维。同时，对于中学物理光学部分的教学，提出了一些建议。

关键词：光路可逆原理；半波损失；几何光学；波动光学

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2023）5-0060-3

1 问题的提出

光路可逆原理同时适用于光的反射现象和光的折射现象，在教材中表达为：让光逆着反射光（折射光）的方向射向镜面（从水或其他介质射向空气）时，反射光线（折射光线）逆着原来的入射光线射出［1］。教材中还通过实验验证其正确性。该原理是初、高中物理教学中几何光学部分的一个重要知识点，也是教学研究的热点［2-6］。笔者在教授该知识时，有学生在研究光射到既可以发生反射也可以发生折射的介质表面时，提出了新的情境，并指出该情境与所学的光路可逆原理相悖，对光路可逆原理的正确性提出了质疑。该情境如下：

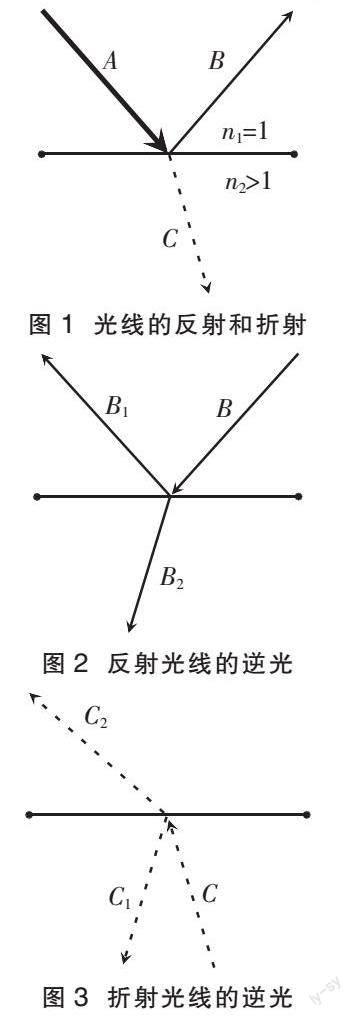
如图1所示，一束光线A（图中用粗实线表示）照射到两种介质的分界面，假设该界面半反半透，且上方介质的折射率n1=1，下方介质的折射率n2>1。反射光线为B（图中用细实线表示），折射（透射）光线为C（图中用虚线表示）。

若根据光路可逆原理，分别分析B和C的逆光路。

對B：反射光线逆光路依然会在分界面上半反半透，反射光线为B1，折射光线为B2，如图2所示。

对C：折射光线逆光路在分界面上也会半反半透，反射光线为C1，折射光线为C2 ，如图3所示。

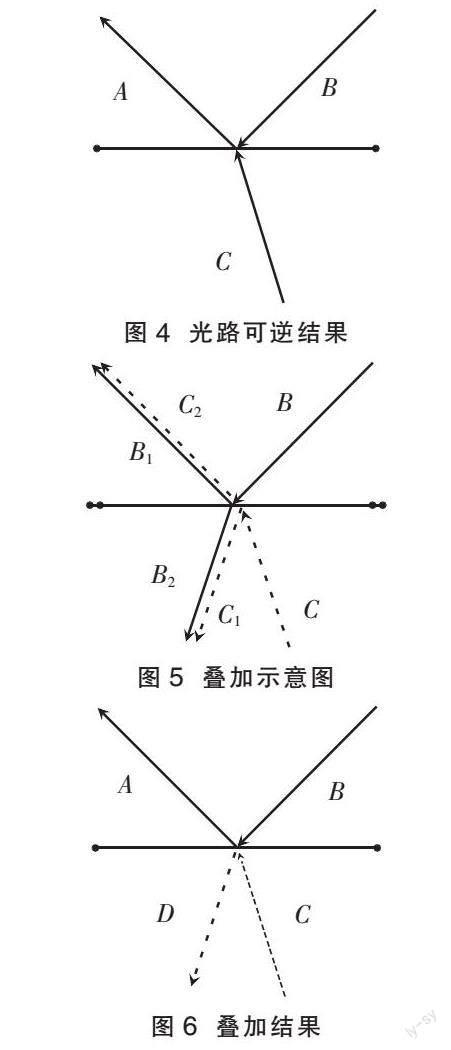
根据光路可逆原理，将B和C的逆光路叠加，可得到图1的逆光路，此逆光路图应该如图4所示。但将图2和图3叠加后，结果却如图5所示。需要说明的是，为便于观察，将图5中重合的光线错开。对光线进行合并整理后，总的逆光路如图6所示。

显然，图6与图4对比，逆着反射光线和折射光线入射，除了原来的入射光线A，还多出了光线D（图6中用点状虚线表示），逆光路与原光路并不重合。这并不符合光路可逆原理。那么，光线D的存在是否合理呢？光路可逆原理还正确吗？应当如何解释上述情境？

2 问题的分析

在中学物理光学部分的教学中，往往将几何光学和波动光学分离开，进行独立教学，很少涉及需要交叉使用两部分知识才能解决的问题。其实，无论是几何光学、波动光学、量子光学，均可解释光现象，所涉及的内容是相通的，而不是孤立的。

对于上述情境，单纯地从几何光学的角度分析，确实很难自洽，但从波动光学的角度却能轻松解决。欲将上述佯谬讲清楚，我们需要使用波动光学中的一个重要概念：半波损失（半波突变、半波增益）［7-10］。所谓半波损失现象，是指在波从波疏介质射向波密介质而发生反射时，反射波在离开反射点时的振动方向相对于入射波到达入射点时的振动相反，或者说，反射波相对于入射波的相位突变了π，相当于光程减少了半个波长。因此在光学中，当光由光疏介质（如图1中n1=1的上方介质）射向光密介质（如图1中n2>1的下方介质）的分界面上发生反射时，反射光与入射光相比会产生半波损失。而当光由光密介质射向光疏介质，在两介质的分界面上发生反射时，则不会产生半波损失。透射（折射）时，无论从哪边入射，均不产生半波损失。

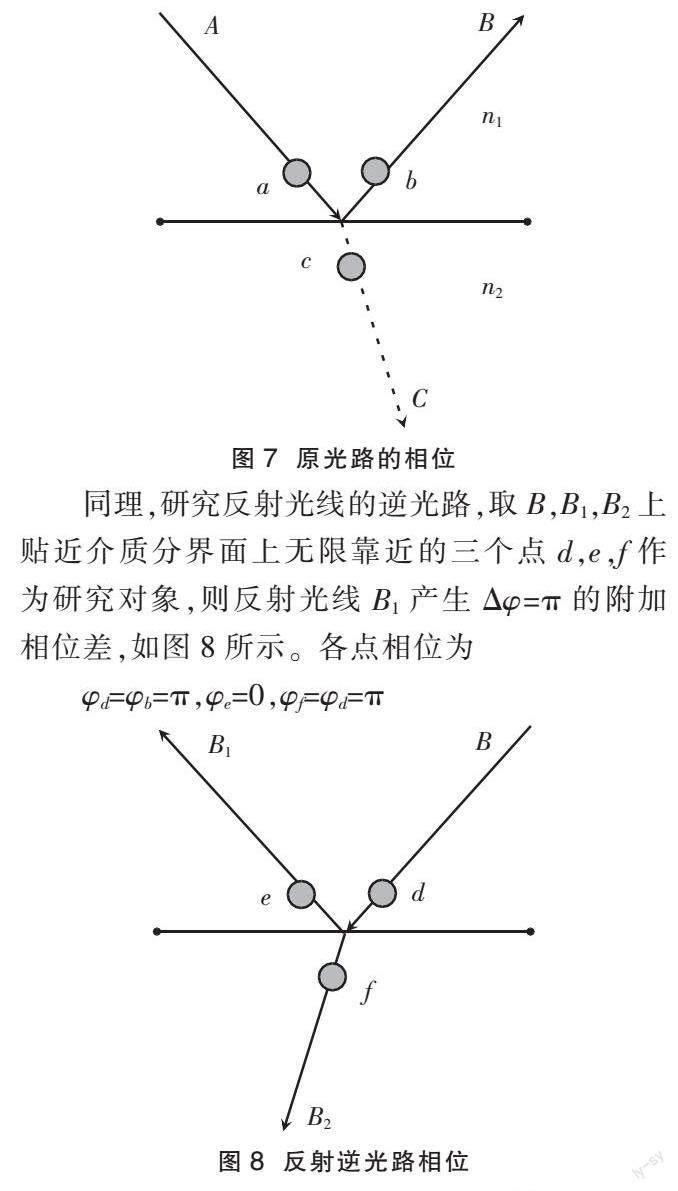
了解了半波损失，光从n1=1的介质中射向n2>1的介质，在发生反射时，恰好满足从光疏介质射向光密介质的条件，则反射光线B会产生Δφ=π的相位差，而折射光线不产生相位差。我们不妨取A，B，C光线上贴近介质分界面上无限靠近的三个点a，b，c，分别研究其相位情况，如图7所示。因只关注相位差，为了简便起见，令A光线上a点此时的相位为φa=0，则考虑到半波损失，此时另外两点φb=π，φc=0。

同理，研究反射光线的逆光路，取B，B1，B2上贴近介质分界面上无限靠近的三个点d，e，f作为研究对象，则反射光线B1产生Δφ=π的附加相位差，如图8所示。各点相位为

φd=φb=π，φe=0，φf=φd=π

对于折射光线的逆光路，由于光从n2>1的介质中射向n1=1的介质，在发生反射时，不满足从光疏介质射入光密介质的条件，故不发生半波损失。取C，C1，C2上贴近介质分界面上无限靠近的三个点g，h，i作为研究对象，如图9所示，各点相位为

φg=φc=0，φh=φg=φc=0，φi=φg=φc=0

将反射光线的逆光路和折射光线的逆光路合成即得图5所示情境。从几何光学简单分析B2和C1叠加构成了图6中多出的D光线。现从波动光学出发，结合上述a～i各点的相位分析可得φh=0，φf=π。这些点无限靠近入射点，可以理解为没有空间距离，只有相位差。因为无穷近，所以相位差只有π，即B2和C1两束光线的相位差Δφ=π。则两束光线正好是反相的，相互抵消，能量为零，亦即D光线实际上并不存在。B1和C2两束光线对应的相位相同，两者叠加后即为原入射光线A。由此可以得出，在光射到既可以发生反射也可以发生折射的介质表面时，光路可逆原理依然成立。

3 思考和启示

以光路可逆原理的一个佯谬为例，说明了几何光学与波动光学的紧密联系。我们在研究光现象时，可以从几何光学、波动光学、量子光学等多角度独立研究，但更要注重各个角度的关联和融会贯通，在日常教学中着重培养学生多角度看待问题的能力。

半波损失作为波动光学中的重要概念，对于我们理解诸多光学现象有着重要意义。除本文所列情境外，对于学生理解诸如增透膜、增反膜等问题也至关重要。在日常教学中，是否补充半波损失相关知识，值得商榷。

光的半波损失产生原因的严格证明，需要用到菲涅尔公式［11］，对中学生难度较大。但笔者认为，可以类比机械波中的驻波，当一端固定时对应有半波损失，当一端自由时对应无半波损失。通过类比的方法，让学生定性认识半波损失产生的原因，以期达到较好的教学效果。最后，感谢张启迪老师公众号“杠精学物理”的启发和帮助。

参考文献：

［1］义务教育物理课程标准实验教科书编写组.义务教育教科书物理（八年级上）［M］.北京：人民教育出版社，2012.

［2］胡象岭.光路可逆原理及其教学价值［J］.中学物理，1995，23（2）：18-19.

［3］陈征燕.光路可逆原理在光学问题中的应用［J］.物理教学，1998，20（10）：36-37.

［4］邵世鑫，张伯贤.光路可逆原理在解题中的应用［J］.中学物理教学参考，1986，15（6）：13，36.

［5］颜国英，张皓晶，姬影，等.探究光路可逆性原理的自制教具［J］.湖南中学物理，2019，34（5）：73-75.

［6］吕宗禄.光路的可逆性原理及其应用［J］.中学物理，1986，14（4）：13.

［7］梅妍，于游.光的半波损失研究［J］.广西物理，2022，43（1）：56-60.