二次分形螺线纺丝头设计及其对场强的影响

刘延波 周聪 郝铭 胡晓东 杨波

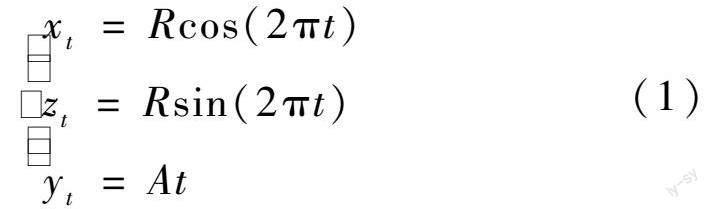
摘 要：为了制备一种所需电压小，能耗低，且生产纤维直径分布窄，品质优良的二次分形螺线静电纺丝头。首先从圆柱螺旋线入手，通过空间坐标变换，獲得二次分形螺线的参数方程，实现了二次分形螺线数学模型的建立；再使用二次分形螺线参数方程建立分形螺线纺丝头的纺丝单元机械模型，多个纺丝单元组合构成阵列式纺丝头；最后在保持其他变量不变的情况下依次改变：一次半径、一次螺距、二次半径、二次扰动圈数、金属丝半径，利用有限元分析软件对二次分形结构螺旋形纺丝头场强分析，结合实际情况确定了分形结构的最佳参数为：一次半径为80 mm、一次螺距为60 mm、二次半径为10 mm、二次扰动圈数为40、金属丝半径为0.2 mm。该条件下的平均电场强度为31.8 kV/cm、场强不匀率为7.53%，表明该结构纺丝头能有效地降低纺丝时所需的电压，且场强的均匀性会使得纺出的纳米纤维分布均匀。

关键词：静电纺丝；二次分形螺旋结构；有限元分析；电场强度

中图分类号：TS104.76

文献标志码：A

文章编号：1009-265X（2023）03-0012-09

基金项目：国家自然科学基金项目（51973168）；“武汉英才”湖北省武汉市高层次人才项目（武财行［2022］734）

作者简介：刘延波（1965—），女，吉林农安人，教授，博士，主要从事静电纺丝技术与原理方面的研究。

通信作者：杨波，E-mail： ybo@wtu.edu.cn

静电纺丝是通过电场力牵伸聚合物溶液或熔体来制备纳米纤维的方法，是目前制备纳米纤维的最有效技术之一［1］。现有的静电纺丝技术大致可以分为两类：一类为有针头静电纺丝技术［2］，另一类为无针头静电纺丝技术［3-5］。有针头纺丝技术存在针头易堵、严重的边缘效应［6］。无针头静电纺丝技术为代表的是捷克第一代纳米蜘蛛［7］。Wang等［8］发明的螺旋线圈无针头静电纺丝头，其加压的面积过大，导致能耗过高，纺丝不均匀。

利用分形理论将一次分形螺旋线圈（迪肯大学发明的螺旋线圈式的无针头静电纺丝头）进行再次分形得到二次分形线圈。分形是以分数维度形式形成空间形态，这个形态的每个部位都近似地相似于整体缩小后的图形［11-12］。分形螺线具有自相似性，利用自相似性可提高基于分形结构中螺旋曲线建立的纺丝电极场强的均匀性，利用分形曲线的多纺丝位点特性可以提高电极的电场强度和生产效率，达到节约能源和提高纤维质量的目的。再利用COMSOL Multiphysics5.6二次分形螺旋纺丝头参数优化，其中设计：一次螺线半径、二次螺线半径、二次扰动圈数、螺线线半径、一次螺线螺距。在一个最终参数下得到较高的场强和较低的场强不匀率（CV）值。

1 分形模型确定与模拟

1.1 二次分形结构公示推导

为建立数学模型，需推导出分形螺线的参数方程。一次螺线曲线为圆柱螺旋线，设其螺距为A，一次螺线半径为R，螺圈圈数为t。如图1，螺线可看成点a沿着圆柱外沿向上旋转移动θ角度，一个螺圈即旋转2π角度，由此可得一次螺线的参数方程如式（1）：

基于一次螺线的参数方程，可推导出二次螺线参数方程。设二次螺线在一个一次螺线螺圈的扰动圈数为M，二次螺线半径为r。如图2，二次螺线可看成点c沿着一次螺线的轨迹向上旋转移动γ角度，一个一次螺圈的路程即旋转了2πM角度，由此可得二次螺线参数方程如式（2）：

1.2 二次分形螺线纺丝头电场模拟

1.2.1 二次分形螺线纺丝头电场模拟原理

利用COMSOL Multiphysics5.6应用静电场分析，其基本过程如下：a）将连续的待求区域或结构体离散为有限单元，然后单元间由多个节点相连，离散过程需要建立模型、设置材料属性、选择单元类型、划分网格、施加载荷和约束；b）对离散后进行场函数分析近似描绘变化规律，建立节点方程，加上边界条件对方程进行修改，从而得到最终可解的有限元方程组；c）求解方程组，获得未知节点场变量的值，并根据每个单元的场变量模型求得场内所有节点场变量的值，分析这些节点变量，得到所求问题的解。本文使用到的是COMSOL Multiphysics 5.6软件中AC/DC模块内的静电物理场对静电纺丝过程中的静电场进行模拟，静电场遵循泊松方程式（3）：

1.2.2 二次分形螺线纺丝头电场模型建立

本文的分形螺线模型使用UG软件建立，其步骤如下：a）使用方程定义样条曲线，画出三维空间曲线。再通过扫掠工具，沿着定义的样条曲线扫描得到二次分形螺旋实体。b）为了后期的有限元模拟，需要建立接收装置和纺丝环境两个模型，纺丝环境默认为空气层，接收装置默认为平面接收板，无论是纺丝头还接收板都包裹在空气层之中。在后期使用COMSOL Multiphysics5.6进行静电纺丝电场模拟时，需要建立接收装置和纺丝头。图3是二次分型螺旋纺丝头模型及装配体。

二次分形螺旋纺丝头由5个单元组成，如图4所示，纺丝头的结构参数有：螺线的线半径r0，指分形螺线由三维曲线加粗后形成三维实体的半径；一次螺线半径R，指二次螺线的大螺圈半径，即纺丝头的中心轴到二次螺线的小螺圈中心点的垂直距离；二次螺线半径r，指二次螺线小螺圈的半径；一次螺线螺距A，指二次螺线的大螺圈从原点螺旋上升360°的垂直距离，即相邻两单元的垂直距离；二次螺线扰动圈数M，指一个单元一次螺线的大螺圈上小螺圈的圈数。同时，取纺丝头正对接收板垂直方向左右30°范围内的顶点作为纺丝位点，以二次分形螺线纺丝头二次螺线扰动圈数为40圈的侧视图为例，令最中间的纺丝位点为0号位点，0号位点左边为负数号位点，0号位点右边正数号位，根据二次螺线公式计算出各纺丝位点的坐标以获得场强值。

1.3 电场模拟实验

基于上述二次分形螺线纺丝头结构设计，对一次螺线半径、螺线线半径、二次分形螺旋半径、一次螺旋螺距、一次螺旋圈数、二次扰动圈数进行有限元模拟。利用COMSOL Multiphysics5.6分别进行电场场强模拟计算。其中图5是二次分形纺丝头场强分布图（后述为了便于表示，场强分布只截取靠近接收板侧一部分）。由表1表示二次分形纺丝头结构参数汇总。

2 结果与分析

2.1 一次半径对场强影响

使用COMSOL Multiphysics5.6软件对不同一次螺线半径（如表1第1组数据所示）的纺丝头装配体进行模拟计算，可获得纺丝头的电场云图及各纺丝位点的场强值大小。电场云图可直观展示纺丝头4个单元正对接收板顶部的电场分布情况，场强颜色越接近红色表示场强越大，场强颜色越接近蓝色则表示场强越小，如图6所示。

由图6（a）可知：同一个模型单元一和单元四、单元二和单元三电场强度基本上相同。是因为纺丝电极的形状整体上呈中心对称，使得在施加外电场后纺丝电极上的电荷分布对称。不同模型相同的纺丝单元，可以看出红色区域逐渐加深，表示电场逐渐增强。由图6（b）可知，随着一次半径的逐渐增大，场强的最大值、场强平均值、平均CV值也随之逐渐增大。可能在其他条件不变的情况下，增大一次半径使得在单个纺丝单元上的纺丝位点之间的距离增加，即二次螺距增大，从而导致各纺丝位点之间的场强相互抵消会减小。其中CV值越大代表离散性越大，直接表明场强分布越不均匀。在一次半径改变的情况下，不同纺丝位点的电场强度分布CV值的变化趋势可以从图6（b）中看出，CV值的变化不是很明显，且均低于10%，表明具有良好的场强均匀性。综合考虑电场强度与场强分布，选择当一次半径为80 mm时纺丝电极场强度与场强分布较佳，场强最大值19.3 kV/cm，场强平均值16.2 kV/cm，平均CV值4.95%。

2.2 一次螺距对场强影响

使用COMSOL Multiphysics5.6软件对不同一次螺线螺距（如表1第2组数据所示）的纺丝头装配体进行模拟计算，可获得纺丝头的电场云图及各纺丝位点的场强值大小，如图7所示。

如图7（a）所示，随着螺距的增加，中间两个电极的电场云图中红色区域逐渐变大。表明随着螺距的增加，纺丝单元之间的边缘效应逐渐减小。这是由于纺丝单元的间距较小时，纺丝单元之间同性电荷所产生的库伦力更加明显。如图7（b）所示，场强CV值也随着螺距的增大而逐渐降低。但是考虑到实际静电纺丝过程中，如果因为螺距过大而导致的产品均匀性较差，这个问题是没有其他措施来改善的，因此选择一次螺距为60 mm为较佳参数，场强最大值17.9 kV/cm，场强平均值15.2 kV/cm，平均CV值12.0%。

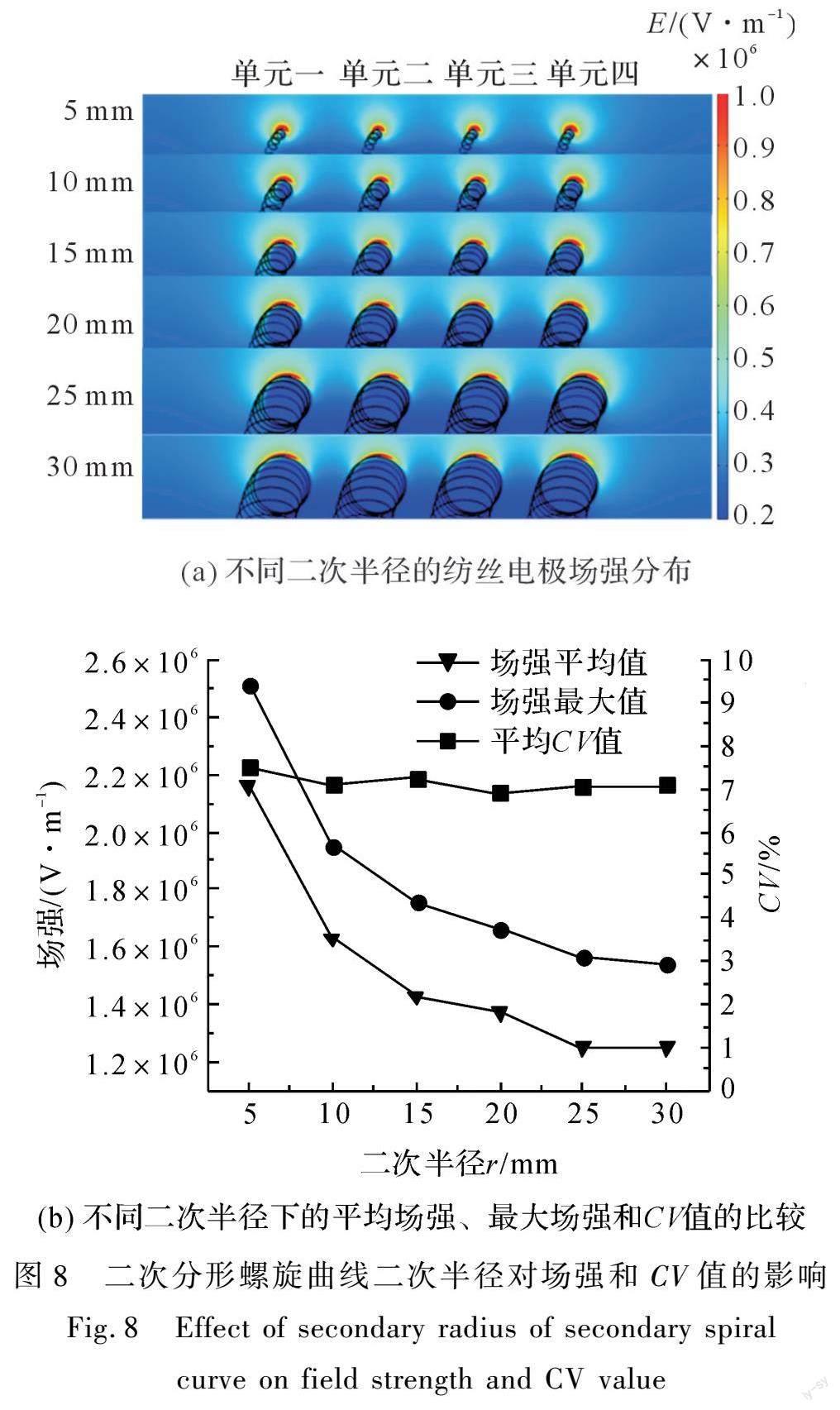
2.3 二次半径对场强影响

使用COMSOL Multiphysics5.6软件对不同一次螺线螺距（如表1第3组数据所示）的纺丝头装配体进行模拟计算，可获得纺丝头的电场云图及各纺丝位点的场强值大小，如图8所示。在其他条件相对不变的情况下，随着二次半径的增大各个纺丝位点的电场强度均下降，可能是因为当二次半径较小时，纺丝电极上的二次扰动螺旋线圈的曲率更大，因此纺丝电极靠近接收装置部分的表面所带电荷密度高，在施加相同外加电压的同时所产生的电场强度就会越大。随着二次半径的逐渐增大，纺丝电极的二次分形螺旋线圈的曲率逐渐减小，电场强度也随之下降，各位点之间的相互排斥作用没有明显的改变，导致场强分布情况大致相同，CV值也接近。当二次半径为10 mm时具有较高的电场强度与更好的均匀性作为较佳参数。场强最大值19.5 kV/cm，场强平均值16.3 kV/cm，平均CV值7.09%。

2.4 扰动圈数对场强影响

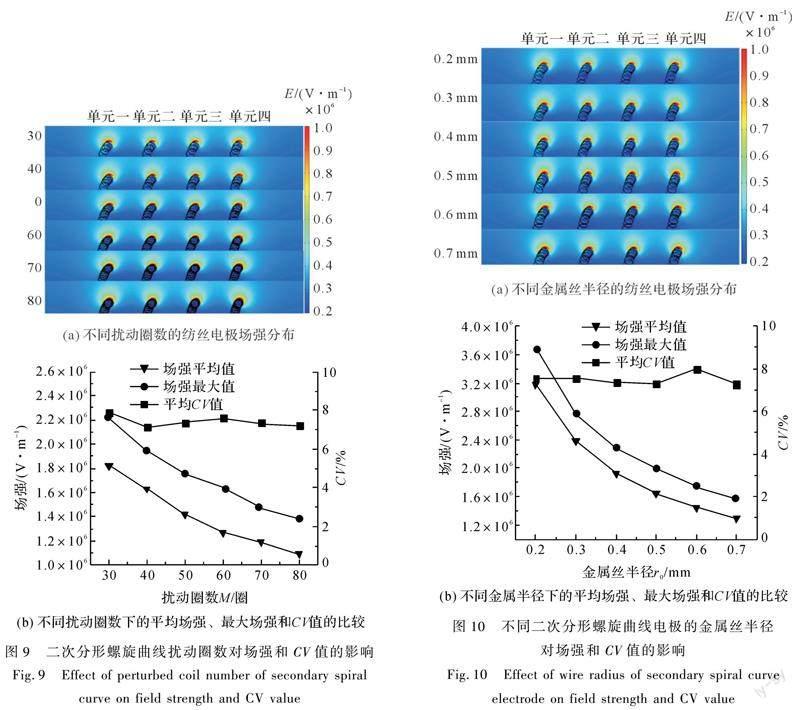
使用COMSOL Multiphysics5.6软件对不同一次螺线螺距（如表1第4组数据所示）的纺丝头装配体进行模拟计算，可获得纺丝头的电场云图及各纺丝位点的场强值大小，如图9所示。随二次扰动圈数的增多，纺丝电极附近的红色区域在减少，表示场强在逐渐降低。主要是因为在不改变其他条件的情况下，增加扰动圈数就是减少了二次扰动线圈之间的距离，同时要分配扰动圈数的电场强度更高，根据电场叠加原理，各二次扰动线圈受到相邻线圈的库仑斥力，使得在这两方向上的电场强度矢量相互抵消，从而導致纺丝电极上各个纺丝位点的电场强度下降。如图9（b）所示随着二次扰动圈数的增多，电场强度降低得十分显著，但是相邻两个纺丝单元之间的距离相对于减小，从而场强变化值不大，各纺丝位点的场强CV值呈下降趋势，但下降得并不明显。因此综合考虑，选择扰动圈数为40圈为较佳参数。场强最大值19.4 kV/cm，场强平均值16.3 kV/cm，平均CV值7.12%。

2.5 金属丝半径对场强影响

使用COMSOL Multiphysics5.6软件对不同一次螺线螺距（如表1第5组数据所示）的纺丝头装配体进行模拟计算，可获得纺丝头的电场云图及各纺丝位点的场强值大小，如图10（a）所示。随着金属丝半径的逐渐增加，电场云图红色区域逐渐减小，电场强度明显降低。随着金属丝的半径逐渐增大，曲率也随之逐渐降低，同时增加纺丝头的整体分配场强的体积，所以表面电荷密度减少，所以施加相同电压时电场强度会降低。如图10（b）所示，而CV值没有明显的变化。考虑到实际生产中制备线径为0.2 mm即金属丝半径为0.1 mm十分困难，所以选择金属丝半径为0.2 mm作为较佳参数。场强最大值37.2 kV/cm，场强平均值31.8 kV/cm，平均CV值7.53%。

2.6 与传统螺线纺丝头对比

分形螺线纺丝头与传统纺丝头场强对比如表2所示，发现圆柱形纺丝头和传统螺线纺丝头的场强平均值、场强最大值比二次分形螺线纺丝头的小，CV值比二次分形螺线纺丝头的值大。传统螺线形纺丝头可以看作圆柱形纺丝头进行一次分形，分型后螺线形纺丝头的金属丝变得更细，纺丝位点处电荷量增加，使得电场强度增大，在进行一次分形后场强值得到显著提升。且圆柱形纺丝位点主要在两侧，有严重的边缘效应，而传统螺线纺丝头纺丝位在中间拥有很多纺丝位点，边缘效应没圆柱形明显，因此传统螺线纺丝头CV值比圆柱形纺丝头低。进行二次分形螺线纺丝头通过分形后获得更细的金属丝，纺丝位点处电荷量增加更加显著，所以比传统螺线纺丝头场强值更高。且通过分形在二次分形螺线纺丝头中间处产生更多的纺丝位点，因此二次分形螺线纺丝头CV值比传统螺线纺丝头低。

3 结 论

通过二次分形螺线纺丝头的设计，对其场强的有限元模拟，主要结论如下：

a）在其他条件相对不变的情况下，纺丝电极的电场强度会随着一次半径或者一次螺距的增加而逐渐增加，会随着二次半径、二次扰动圈数或者金属丝半径的增加而逐渐减小。电场强度的分布即CV值则是随着一次半径的增大而增大，随着一次螺距的增加而减小，其他参数对场强CV值的影响不大。

b）根据电场强度与分布均匀性在结合实际情况下得到最佳的分形结构纺丝电极的结构参数：一次半径R为80 mm、一次螺距A为60 mm、二次半径r为10 mm、二次扰动圈数M为40、金属丝r0半径为0.2 mm。最大场强值和平均场强值有极大的提高，CV值大幅度降低。其中场强最大值37.2 kV/cm，场强平均值31.8 kV/cm，平均CV值7.53%。在纺丝过程中可以激发多个射流，并且能够节约电荷，从而达到节约电源，在实际生产中十分有意义。

参考文献：

［1］苏芳芳，经渊，宋立新，等.我国静电纺丝领域研究现状及其热点：基于CNKI数据库的可视化文献计量分析［J/OL］.东华大学学报（自然科学版），2022：1-11.DOI：10.19886/j.cnki.dhdz.2022.0347.

SU Fangfang， JING Yuan， SONG Lixin， et al.Present situation and hotspot of electrospinning in China： Visual

bibliometric analysis based on CNKI database［J/OL］. Journal of Donghua University （Natural Science）， 2022：1-11.DOI：10.19886/j.cnki.dhdz.2022.0347.

［2］李建軍，季骥，王丽秋.圆环状辅助电极对多针头静电纺丝系统的电场分布影响［J］.现代纺织技术，2019，27（3）：91-96.

LI Jianjun， JI Ji， WANG Liqiu.Effects of circular ring auxiliary electrode on electric field distribution of mult-needle electrospinning system［J］. Advanced Textile Technology， 2019， 27（3）： 91-96.

［3］高璐璐，徐岚.批量制备静电纺有序纳米纤维的研究进展［J］.现代纺织技术，2021，29（2）：7-21.

GAO Lulu， XU Lan.Research progress of batch preparation of electrospun aligned nanofibers［J］. Advanced Textile Technology， 2021， 29（2）： 7-21.

［4］谢概，宋庆松，邓德鹏，等.无针头静电纺丝研究进展［J］.工程塑料应用，2014（6）：117-121.

XIEGai， SONG Qingsong， DENG Depeng， et al. Research progress of needleless electrospinning［J］. Engineering Plastics Application， 2014（6）： 117-121.

［5］张艳萍，张莉彦，马小路，等.无针静电纺丝技术工业化进展［J］.塑料，2017（2）： 1-4.

ZHANG Yanping， ZHANG Liyan， MA Xiaolu， et al. Recent development of industrialized needleless electros-pinning technology［J］. Plastics， 2017（2）： 1-4.

［6］王金龙，付翀，李清馨，等.静电纺丝法制备SnO2纳米纤维及其气敏性能研究［J］.西安工程大学学报，2021，35（4）：43-49.

WANG Jinlong， FU Chong， LI Qingxin， et al. Preparation of SnO2 nanofibers by electrostatic spinning and their gas-sensing properties［J］. Journal of Xi'an Polytechnic University， 2021， 35（4）： 43-49.

［7］JIRSAK O， SANETRNIK F， LUKAS D， et al. Method of nanofibres production from a polymer solution using electrostatic spinning and a device for carrying out the method［Z］. US. 2009

［8］WANG X， NIU H， WANG X， et al. Needleless electros-pinning of uniform nanofibers using spiral coil spinnerets［J］. Journal of Nanomaterials， 2012， 2012： 1-9.

［9］MANDELBROT B， B. Stochastic models for the Earth's relief， the shape and the fractal dimension of the coastlines， and the number-area rule for islands［J］. Proceedings of the National Academy of Sciences of the United States of America， 1975， 72（10）： 3825-3828.

［10］段青山，安潔洁，黄崇杏，等.分形理论应用于包装材料性能研究的进展［J］.包装工程，2021，42（1）：55-67.

DUAN Qingshan， An Jiejie， HUANG Chongxing， et al.Progresses on application of fractal theory in research of packaging materials properties［J］. Packaging Engineering， 2021， 42（1）： 55-67.

［11］王璐祯，李超.分形理论在产品可持续设计中的应用研究［J］.设计，2022，35（15）：140-143.

WANG Luzhen， LI Chao. Study on the application of fractal theory in sustainable product design［J］. Design， 2022， 35（15）： 140-143

［12］杨雨露，李晶源.分形理论在室内设计中的应用分析［J］.设计，2019，32（23）：155-157.

YANGYulu， LI Jingyuan. Application analysis of fractal theory in interior design［J］. Design， 2019，32（23）：155-157.

［13］张智云.二次分形螺旋斜弹簧的数学建模［J］.机电元件，2018，38（5）：25-28.

ZHANG Zhiyun.The mathematical modeling of secondary helical oblique springs［J］. Electromechanical Components， 2018， 38（5）： 25-28.

［14］刘延波，罗鑫，郝铭，等.螺线式无针头静电纺丝过程中场强的分布与改善［J］.天津工业大学学报，2021，40（4）：38-44.

LIU Yanbo， LUO Xin， HAO Ming， et al. Distribution and improvement of field strength in spiral coil needleless electrospinning process［J］. Journal of Tiangong University， 2021， 40（4）： 38-44.

Abstract： The electrospinning technology is a method to stretch polymer fluids for fabricating nanofibers with diameters of tens to thousands of nanometers under the electrostatic field force， which is simple， widely applicable， and the most promising in the industrialization of nanofibers. At present， the preparation of large-scale electrospun nanofibers includes needle type and needleless type. Compared with the needle electrospinning technology， the needleless electrospinning technology has the advantages of zero needle clogging problem， easy cleaning and significantly higher production efficiency. However， the current needleless electrospinning technology used for the industrial preparation of nanofibers requires a high spinning voltage， which may break down the air， resulting in great safety hazards， high energy consumption， wide diameter distribution and poor quality of the fibers. The fractal spiral has a self-similarity characteristic， which can improve the uniformity of the field strength of the spinning electrode based on the spiral curve in the fractal structure. The multi-spinning site characteristics of the fractal curve can improve the electric field strength and production efficiency of the electrode， so as to save energy and improve the fiber quality. Firstly， we start with the cylindrical spiral， and obtain the parametric equation of quadratic fractal spiral through space coordinate transformation， establishing the mathematical model of quadratic fractal spirals. Then， the mechanical model of the spinning unit of the fractal spinning needle is established by using the quadratic fractal spiral parameter equation， and multiple spinning units are combined to form an array of spinning needle. Finally， we change the following variables in turn while keeping other variables constant： primary radius， primary pitch， secondary radius， number of secondary disturbing turns and wire radius. By using finite element analysis software， the field strength of the spiral spinning needle with quadratic fractal structure is analyzed and the optimal structure is obtained. It is found that the electric field strength and CV value increase with the increase of the primary radius. The increase of the primary pitch can increase the electric field strength but decrease the CV value. The increase of the secondary radius， the number of secondary perturbations turns and the radius of the wire can lead to a decrease in the field strength value and has few effects on the CV value. Combined with the actual situation， the optimal parameters of fractal structure are determined as follows： primary radius of 80 mm， primary pitch of 60 mm， secondary radius of 10 mm， number of secondary disturbance turns of 40 and wire radius of 0.2 mm. The average electric field strength is 31.8 kV/cm and the CV value of the field strength is 7.53%. The results show that the structure of the spinning needle can effectively reduce the voltage required for spinning， and the energy consumption is low. Moreover， the uniform field intensity will make the electrospun nanofibers evenly distributed， which is of significance to be referred for the actual industrial production of nanofibers.

Keywords： electrospinning; secondary spiral structure; finite element analysis; electric field strength