多基地果蔬农产品供应链物流优化

张嘉毅，刘 欢，李钊钊，樊慧慧，唐彭燕

（甘肃农业大学 信息科学技术学院，甘肃 兰州 730000）

0 引言

果蔬农产品作为农贸市场流通中不可或缺的一部分，应保证其供应链完整性，对其物流模式进一步优化，以保障果蔬农产品的质量和物流服务水平［1］。果蔬农产品供应链是将农产品从产地送到餐桌的过程，人们对果蔬农产品的生鲜程度要求较高，而果蔬农产品容易受到运输环境的影响，保质期较短，因此对物流运输要求较高。好的运输路径不仅可以降低果蔬农产品的运输时间、减小运输路程，还可以降低果蔬农产品的货损，节约物流成本［2］。然而目前果蔬农产品供应链体系仍不够完整，主要体现在运输成本高、物流损失严重、物流信息不健全等方面，因此健全供应链体系、实现高效率物流运输是时代的必然趋势。

1 相关研究

物流运输中的车辆路径问题（Vehicle Routing Problem，VRP）［3］自提出以来一直是路径优化领域的研究热点，目前对VRP 的研究多集中在客户需求、车辆配置、电子商务等方面。在实际运输过程中影响最优路径的主观与客观因素有很多，某些因素在研究中被人为地模糊处理，多着重处理运输成本方面的问题。例如，包贤哲等［4］针对路径规划提出一种变异扩散蚁群算法，通过极值限定信息素浓度导致算法停滞，而后采用变异机制提高算法精度，再利用信息素扩散加快较近蚂蚁之间的交流，加快算法收敛；唐慧玲等［5］构建了多目标的VRP 线性规划模型，采用改进蚁群算法求解，其在蚂蚁信息素中引入混沌扰动机制提高算法适应性，同时对启发因子、状态转移概率和信息素更新进行优化提高搜索效率；Nie 等［6］提出将神经网络引入复杂模型中得到新的蚁群优化算法，以解决三维路径中效率的规划问题；方文婷等［7］针对蚁群算法信息素不足收敛慢的问题，将A*算法的全局收敛性与蚁群算法的正反馈性相结合，构建了混合蚁群算法来解决路径优化问题；Wu 等［8］提出一种新的改进遗传算法，利用贪心算法确定初始种群，然后设计一种新算子作为组内头对头变异算子，使其进化更加确定和有效；玄世龙等［9］提出一种优化的禁忌算法，将已搜索路径放入禁忌表中迭代，最后对结果进行比较，寻找最优路径，结果表明此算法较A*算法更可行有效；邱志平等［10］提出一种多目标禁忌搜索算法，该算法在原有基础上增加了禁忌搜索算法和帕累托解的融合机制、优秀解保留机制、多方向搜索等，最后又与遗传算法相结合产生此算法；刘倚玮等［11］提出在考虑约束条件的基础上运用Dijkstra-GA 混合算法和模拟退火算法进行优化，通过仿真实验得出此算法可以有效规划路线；惠海波等［12］为减少DV-Hop 算法的定位误差，改进模拟退火算法使其避免重复搜索，提高全局搜索能力，仿真结果表明该算法可行；Wu 等［13］提出在无人机输电铁塔巡检路径中结合模拟退火算法求出最优能耗路径，然后搭建模型进行数据分析，得出该算法提高了效率；徐胜等［14］为解决旅行商的停滞问题，提出基于遗传-模拟退火的蚁群算法，采用遗传算法增加解的多样性，模拟退火算法提高解的质量，得出新算法具有较好解的能力。

由上述文献研究可知，大部分VRP 研究中带有时间窗。本文从带有时间窗和容量约束的VRP 两方面进行研究，利用启发式算法［15］将这两个因素联合决策，寻找最优解。本文选择的启发式算法为蚁群算法［16］，在前人研究的基础上增加时间、载重、需求等约束条件改进算法，用于解决带有时间窗的VRP，以优化多基地果蔬农产品供应链的物流问题。

2 问题描述

本文研究西北地区的果蔬农产品供应链物流优化问题，以甘肃省、青海省为例，其整体供应基地点和接收点分布如图1 所示。已知供应基地和其他接收点的坐标位置，同时考虑接收点的需求量、可接受的时间窗（运输时间+服务时间）、运输车辆的载重量等。现有多辆运输车由供应基地运送农产品到各个接收点，在满足约束条件下，得到运输车辆所用距离成本最小的最优路径。

建模时作出以下假设：①路径优化目标值不受车辆状态影响（动力充足、型号统一等）；②每条路径接收点总需求量不超过运输车辆的极限承重；③每个接收点都必须被经过；④每一个接收点仅能一辆车经过且运输车最终返回出发点；⑤允许运输车辆提前走到目标点，同时必须满足该点时间窗，如果产生时间损失成本则重置路径；⑥运输车辆若晚到目标点，超出时间窗则加入惩罚成本，同时算法设计中对该路径进行重置；⑦不考虑对一个接收点多次运输。

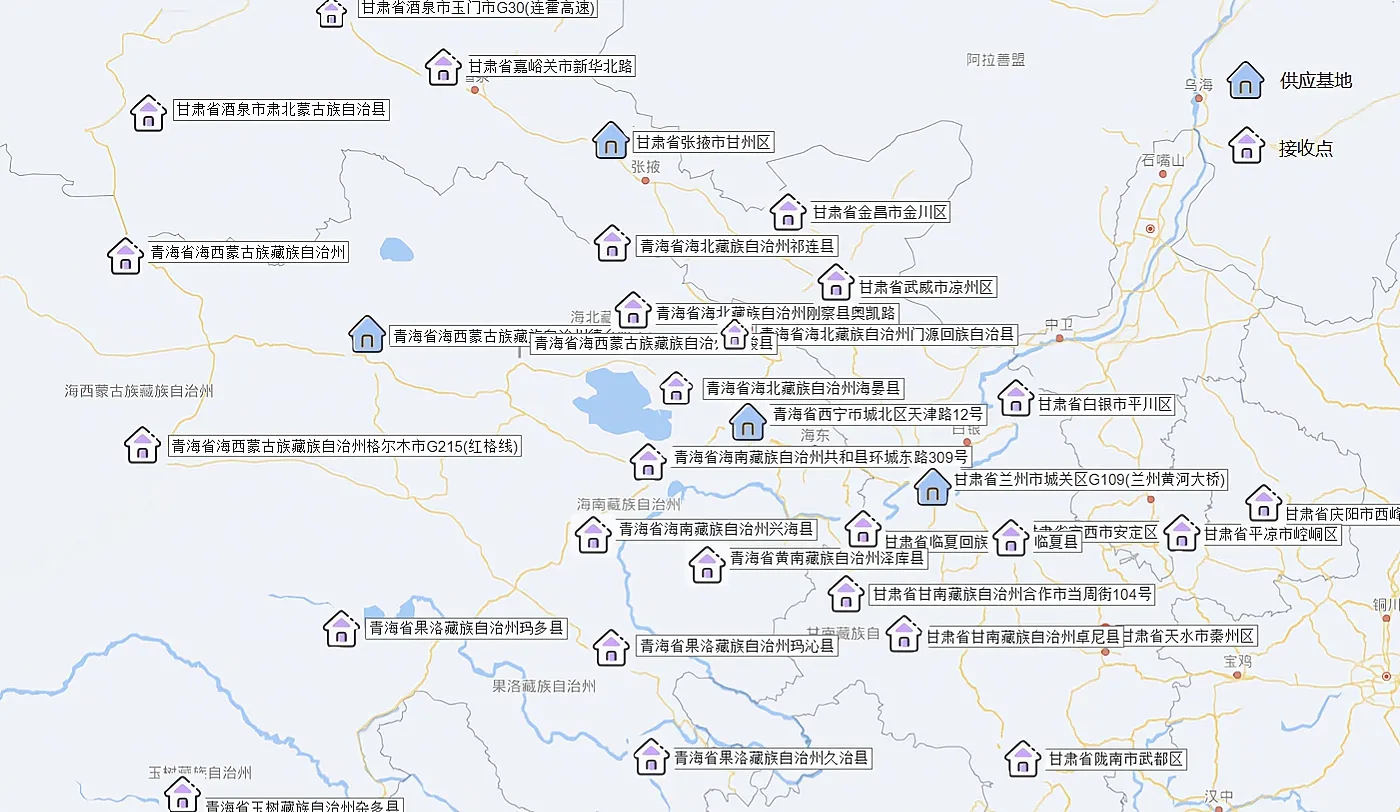
Fig.1 Distribution of overall supply base points and reception points in the northwest图1 西北整体供应基地点和接收点分布

3 模型建立

本文模型相关变量的定义如表1所示。

Table 1 Definition of variables表1 相关变量定义

模型中包含物流运输时整体路径的时间成本，以及运输过程中考虑果蔬农产品因存储环境而产生的损失值，且加入保证产品质量的成本，例如制冷材料等，根据以上条件建立如下目标函数：

式中，ZC1表示车辆始发过程中随着时间推移产生的运输成本，表示为：

ZC2表示加入运输过程中保证产品质量的成本，表示为：

ZC3表示产品在运输时以及在接收点的服务时间中因储存环境变化产生的损失值，例如在接收点服务过程中装卸导致的产品损失值，以及在运输过程中受时间影响使得农产品品质下降而导致的成本等，表示为：

ZC4表示加入惩罚时间窗限制，主要用于在整体优化过程中排除一系列运输不及时的问题，在约束条件中对超时进行惩罚计算，表示为：

式（1）—式（6）表示模型需要考虑的成本，在基础运输费用下同时加入因农产品自身问题而产生的损失值，即多基地果蔬农产品运输过程中带有惩罚函数限制的损失模型；式（7）表示每个接收点只可被分配到一条路径；式（8）表示运输过程所有路径的使用车辆数量小于或等于总车辆数量；式（9）表示每次的路径优化都必须回到初始供应基地点；式（10）表示车辆到达接收点完成服务时间后必须离开该接收点；式（11）表示运输路径中有很多规划路径，在逐步求得最优时消除之前存在的路径；式（12）—式（14）表示目标函数中分段函数ZC4的定义域范围，在时间区间不同情况下有不同的惩罚函数，一种是在惩罚时间内的惩罚系数y，一种是超出时间限制的损失系数k，当全部超出时，则产品无价值，此时惩罚成本为产品价值；式（15）—式（16）表示在供应基地和接收点之间的运输时间的限制，接收点只在一定时间内接收运输车辆并且完成该点的服务时间；式（17）表示在既定时间区间内完成运输，则惩罚函数值为0，结果趋向于最优；式（18）表示车辆运输路径中载重量大于或等于各个接收点需求量之和，且等于时为最优；式（19）表示车辆载重为一个参数值，根据实验内容界定；式（20）表示供应基地的存储量必须要大于或等于各个接收点的需求量之和。

4 改进蚁群优化算法

4.1 算法描述

对原始蚁群算法模型作出相应约束改变，将其转换为能够解决多基地带有时间窗的路径优化问题的算法模型。结合研究目的，已知接收点和供应基地坐标，以式（6）目标函数为核心进行优化；加入式（3）—式（4），使得算法输出结果能够考虑上述损失情况，减少相关损失因素干扰。在不断迭代过程中，根据蚂蚁移动的不确定性以及对信息素浓度的选择性构建出最优路径。

4.2 算法流程

根据蚁群算法原理，加入各类约束条件以及优化程度、优化策略，通过对各类参数的灵活定义衍生出不同优化类型，同时在改进蚁群优化算法代码中加入路径分割算法，即将多基地路径分开优化，分别以某个供应基地为主找到所有最优路径，并且将其整合后对比是否为最优，从而解决因局部最优而产生的优化结果偏差。得到各基地中各车辆参数后，在满足运输规模的条件下分配最优接收点。

本文算法参数及设定函数为：

定义接收点坐标集合C以及各个坐标之间的距离dij(1 ≤i≤n，1 ≤j≤n，i≠j)，将出发点和返回点设为同一供应基地。

计算欧几里得距离为：

信息素更新函数为：

式（22）表示蚂蚁在选择路径时会尽量选择距离近的且信息素浓度较大的方向，其中allowedk表示在t时刻蚂蚁k下一步选择的坐标（无访问）；α表示信息启发式因子，反映信息素的相对程度；β表示期望启发式因子，反映期望值的相对程度。式（23）表示坐标i，j转移的期望程度（先验知识），dij越小，ηij(t)越大；式（24）、（25）表示降低信息素，防止启发信息淹没：ρ表示信息挥发系数，模仿人类记忆，防止无限积累，取值范围为［0，1］，1 -ρ表示信息残留系数；式（25）表示本次循环的信息素增量；式（26）表示在原信息素更新加入避免停滞现象的出现，在搜索中动态调整状态转移概率。

本文算法流程为：

步骤1：将时间初始化t=0，循环次数NC=0，设置最大循环次数maxNC=0，路径(i，j)的初始化信息素τij(t)=const，初始时刻Δτij(0)=0。

步骤2：将所有未被访问过的坐标放入集合C。

步骤3：对集合C中元素排列，对于任意i≤j，满足当前路径Si≤Sj（当前路径S最后一个客户），则令k=1。

步骤4：若全被访问完过，则跳至步骤7。

步骤5：当路径合格时，保存当前路径S，重新开辟新路径，从当前集合中未被访问的坐标中重新随机选择另一个坐标作为出发点，同时跳至步骤3。

步骤6：如果优化后选择的坐标合法，则将该坐标加入S路径中，k=k+1，跳至步骤4。

步骤7：根据一系列计算，最后得出目标值min，此时若该路径的接收点出现惩罚时间，以式（16）的时间窗范围为参考，则不会将该返回值加入路径，并重新选择路线，跳至步骤3。

改进蚁群优化算法流程如图2所示。

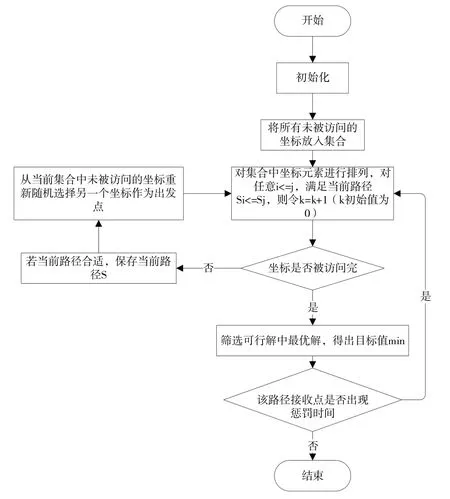
Fig.2 Improved ant colony optimization algorithm process图2 改进蚁群优化算法流程

4.3 算法验证

为验证改进蚁群优化算法的有效性，将其与禁忌搜索算法、模拟退火算法进行比较。随机选取5 个数据集进行测试，每个数据集中均有供应基地点4 个，接收点51 个。5 个数据集参数设置如下：①供应基地和接收点的横纵坐标均为［0，100］的随机数；②供应基地时间窗为［0，12］，所有接收点时间窗均为［0，12］的随机区间；③对所有基地的所有车辆统一极限承重为10 吨；④运输车的车速默认为50km/h；⑤所有接收点的需求量均为［1，4］的随机区间；⑥所有接收点需要处理车辆的服务时间均为0.6。

三种算法的参数设置如下：①改进蚁群优化算法中的信息启发式因子α=1，期望启发式因子β=4，信息素强度Q=20，信息素挥发因子ρ=0.2，蚁群规模popsize=35；②禁忌搜索算法中禁忌表长度TL=8；③模拟退火算法中退火起始温度T0与终止温度Tf关系为T0=10 000Tf，降火速率dT=0.9。以上3 种算法迭代次数均为100 次，分别运行10 次，提取10 次中物流成本的最优解以及其对应的运输时间和车辆使用数，不同算法优化结果如表2 所示。可以看出，在运输时间近似的情况下，改进蚁群优化算法的物流成本和所需车辆数低于禁忌搜索算法和模拟退火算法。

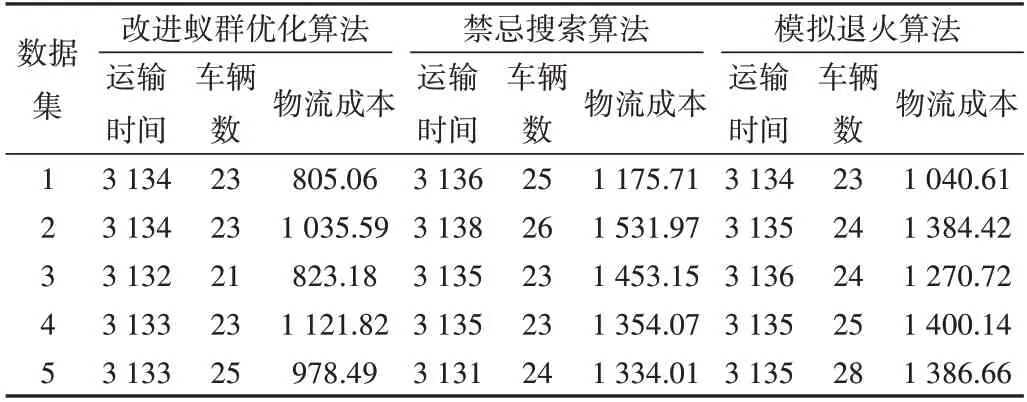
Table 2 Comparison of optimization results of different algorithms表2 不同算法优化结果比较

5 实验分析

5.1 仿真实验

选取西北地区甘肃省、青海省为例的果蔬农产品供应链物流问题，相应的供应基地与接收点的实验坐标如图3所示。

由甘肃省与青海省坐标分布可知居民主要居住城市均匀分布在两省接壤线附近，故选择4 个供应基地（d1-d4）与26个接收点（0-25），具体如表3所示。

5.2 参数实验分析

改进蚁群优化算法中，如果蚂蚁数量过大，则每条路径上的信息素浓度趋于平均，正反馈作用减弱，从而导致收敛速度减慢；如果过小，则可能导致一些从未搜索过的路径信息素浓度减小为0，导致过早收敛，解的全局最优性降低。a为信息启发式因子，其值越小越容易陷入局部最优；β为期望启发式因子；ρ为信息素挥发因子，与全局搜索和收敛速度有关。根据蚁群算法的参数设置如下步骤：

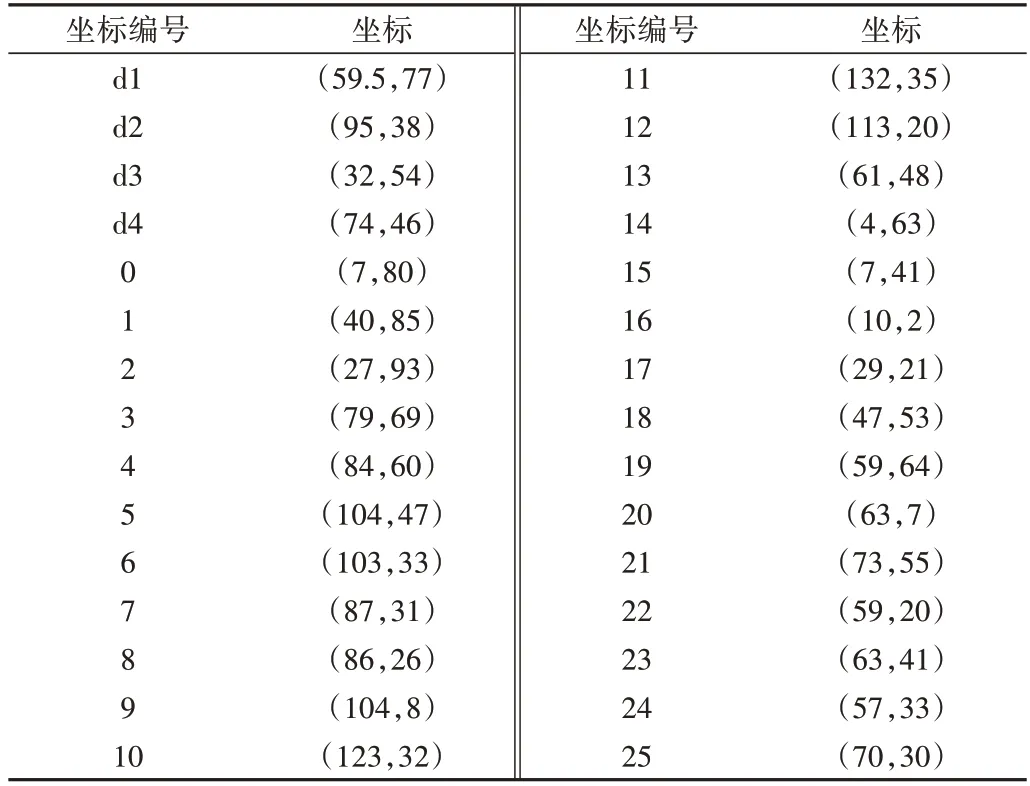
Table 3 Experimental coordinate point表3 实验坐标点

步骤1：确定运输车辆数量，接收点数量/蚁群规模≈1.5。

步骤2：参数粗调，将信息启发式因子a，期望启发式因子β，信息素强度Q设定为取值范围内的较大值。

步骤3：参数细调，信息素挥发因子ρ取值过大时容易影响随机性和全局最优性，因此选取取值范围内的较小值。

改进蚁群优化算法参数空间大且关联性很强，很难确定一种基于各类问题的特殊最优组合模型。本文对同等实验数量的随机坐标进行大量测试，得到最佳参数设置范围为：

0 ≤α≤5，0 ≤β≤5，0.1 ≤ρ≤0.99，10 ≤Q≤100

调整取值范围较大的因子，设置如下：信息启发式因子α=1，期望启发式因子β=5，信息素强度Q=20，信息素挥发因子ρ=0.2。

现存的30 个坐标点中，以供应基地作为物流始发点，为确保整体路径最优，对车辆数目不作限制，即在算法运行中不采用运输车辆数量作为约束条件。本次运输车车速默认为50km/h，每辆运输车的载货量极限承重为10t，每个接收点所需要的货物量区间为［0.5，4］t。通过式（21）以及地图的比例尺求得距离，结合速度求出运输时间。供应基地时间窗包含各个接收点时间窗，将供应基地时间窗设置为［0，12］，接收点时间窗为［0，12］的随机区间，服务时间设为［0.5-1.5］的随机数。

5.3 实验结果与分析

5.3.1 单例验证

首先对单省物流优化验证算法的有效性，以甘肃省为例，取表3 中坐标编号d1、d2 为供应基地坐标，取0-12 为接收点坐标，得到坐标散点图见图4。算法路径优化收敛曲线如图5 所示，设置迭代次数为100 次，迭代后趋于一个稳定数值，即目标优化的距离成本。算法路径优化如图6所示，表示对图4 坐标散点图的路径优化结果。考虑到甘肃省地形狭长，东西跨距过大，运输时间过长，省内整体运输很难由一个供应基地贯穿西北、东南两端接收点，因此在西北方与东南方形成两个独立的运输网。算法运行输出得到最优路径分配方案如表4 所示，同时结合图6 算法路径优化得出5 条优化路径，并且标有每条路径详细的约束参数。根据时间窗设定接收点的服务时间（装卸等）、建议载重量（吨），路径中车辆极限承重大于或等于各个接收点的需求量之和，在得到最优路径的前提下建议车辆的载重量也能同样达到优化目的。在实际物流费用处理时，将所有得到的结果转换为实际参数，例如将时间转换为24h制，分别计算出每个路径的路程，将其累加并与运输费用等进行相关数据处理即可得出最小物流成本。

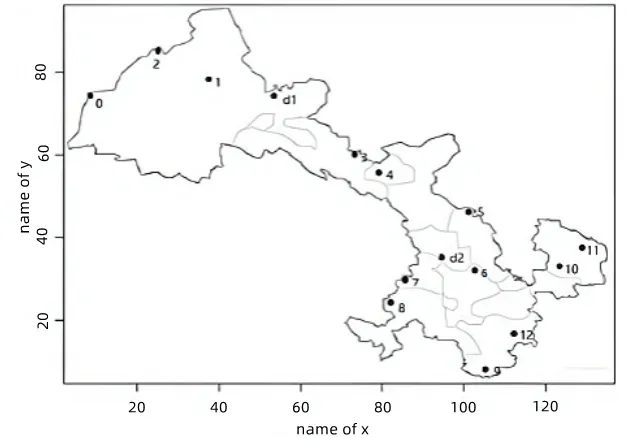
Fig.4 Coordinate scatter map of Gansu province图4 甘肃省坐标散点图

5.3.2 实验应用及分析

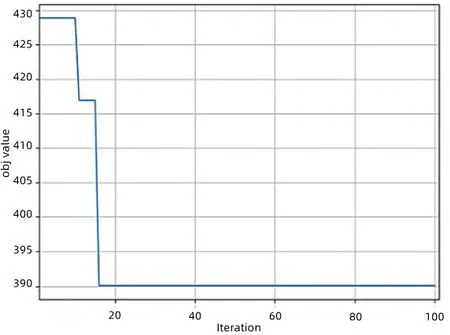
Fig.5 Algorithm path optimization convergence curve of Gansu province图5 甘肃省算法路径优化收敛曲线

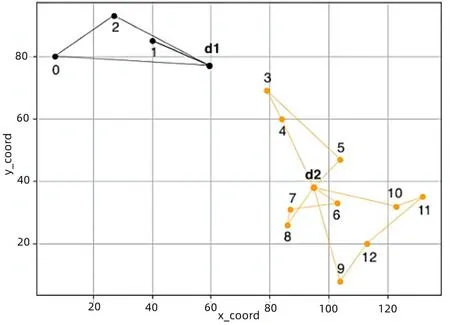
Fig.6 Algorithm path optimization in Gansu province图6 甘肃省算法路径优化

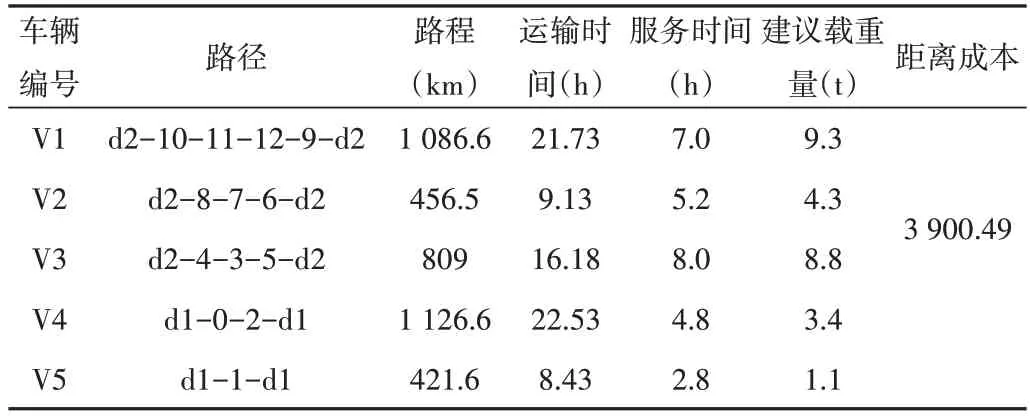
Table 4 Optimal route allocation scheme of Gansu province表4 甘肃省最优路径分配方案

结合图3 西北地区供应基地与接收点的实验坐标，得到图7 所示的西北地区算法路径优化收敛曲线，表示经过迭代运输路程逐渐最优；图8 为西北地区算法路径优化，表示经过算法优化得到11 条路径。为提高运输效率，每个接收点只能经过一次且所有点都要被经过。算法运行输出得到表5 的西北地区最优路径分配方案，其中建议载重量是每辆车在每条路径中每个接收点的需求量之和，用于建议车辆每次出货大致需要的货物量。为使所有实验点都被经过，可能会出现一辆车只运输一个接收点的情况，例如表5 西北地区最优路径分配方案中车辆编号为v3、v8、v10 的车辆，为了增加车辆利用率以及减少距离成本，存在两省接壤处的跨省运输。本次实验共使用11 辆运输车，得到每辆车经过的接收点和每条路径的路程。本次实验加入惩罚时间窗限制，用于在全局优化过程中排除一系列运输不及时问题，在约束条件内对超时进行惩罚计算。以上为制约物流运输成本的主要因素，其中各种因子相互影响，需迭代模拟出最佳运输方案，使运输总成本最小。受载货量的限制，可能有些车辆的路径大致相似，尽管路径能做到大致吻合，但是仍然需要安排两辆运输车。同时若考虑损失函数，为减少农产品因运输、存储环境、装卸过程中的损失，则车辆载重必须要大于建议载重量且小于车辆的极限承重，具体措施可以是增加在冷藏保存方面的用物重量等。

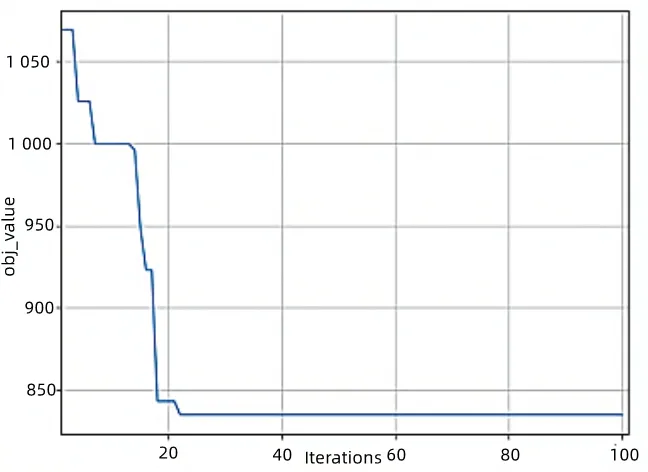
Fig.7 Convergence curve of algorithm path optimization in northwest China图7 西北地区算法路径优化收敛曲线

Fig.8 Algorithm path optimization in northwest China图8 西北地区算法路径优化

6 结语

本文以西北地区的两个省份作为对象构建模型，研究了多基地果蔬农产品供应链物流优化问题，从现实角度出发选择参数，考虑到果蔬农产品会因运输中存储环境产生成本，例如制冷材料等保证生鲜程度的成本，加入核心参数时间窗，在接收点的时间窗内进行路径优化，并且加入带有惩罚系数的时间窗，使优化后的路径不被惩罚结果影响。同时设计多供应基地对多接收点的路径优化算法，利用蚁群算法兼容性强、参数关联性高的特点寻找参数以避免陷入局部最优。优化结果表明，与传统集中物流运输相比，模型得到的优化路径可以减少物流支出。然而，本文算法还有很大改进空间，例如需提高算法的迭代效率和并增加其适用范围，在未来研究中考虑为减少车辆使用损耗而在路径选择中加入对不同载重车辆的选择性，以便于得到更优物流配送方案。

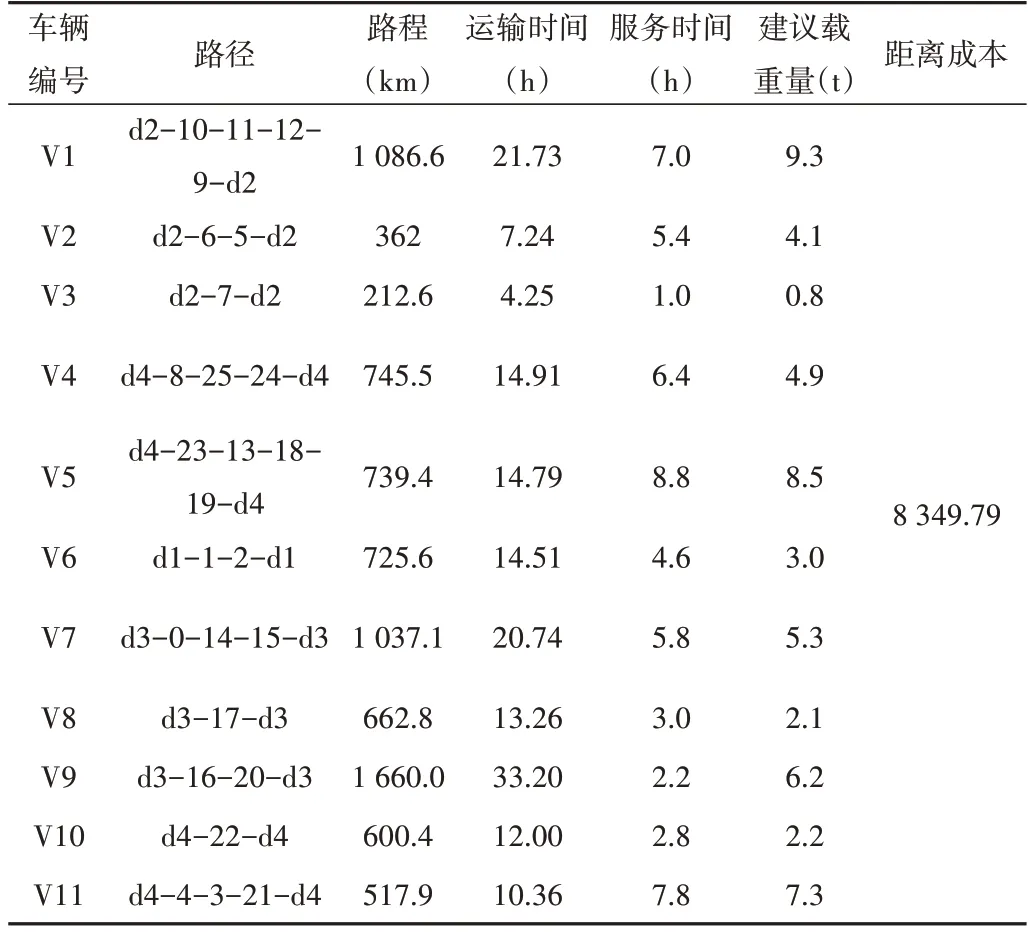
Table 5 Optimal route allocation scheme in northwest China表5 西北地区最优路径分配方案