基于精英反向学习的改进BAS算法
丁瑞成,刘 学,杨孟刚,郑焕祺
(1.山东建筑大学 信息与电气学院,山东 济南 250101;2.山东省产品质量检验研究院,山东 济南 250102;3.山东建筑大学 建筑城规学院,山东 济南 250101)
0 引言
天牛须算法(Beetle Antennae Search Algorithm,BAS)是于2017 年提出的一种模仿天牛觅食过程的群智能算法[1]。与粒子群算法、遗传算法等经典群智能算法相比,BAS 仅采用单独个体代替种群协作,具有参数简单、易于实现等优点,已被广泛应用于电力调度[2]、PID 控制器设计[3-4]、图像处理[5-6]和路径规划[7-8]等领域。然而BAS 算法单独个体的寻优模式虽然简化了寻优过程,但降低了种群多样性。且天牛左右两须的随机搜索机制效率低下,面对高维复杂的寻优问题时极易陷入局部最优值。
国内外学者针对BAS 算法的缺陷提出相关改进措施,例如文献[9]采用基于相似度的混沌迁移策略,同时引入社会学习策略保证种群信息交互,提高了收敛速度与精度;文献[10]提出一种多向感知探路反馈的BAS 算法,通过产生多个方向单位向量,天牛触须在多个方向进行探索,并选取适应度最好的单位向量决定搜索方向,拓展了天牛个体的搜索路径;文献[11]在每次迭代中采用自适应矩估计方法更新每个维度的搜索步长,避免了算法陷入局部最优解。以上改进措施在一定程度上提高了BAS 算法的寻优性能,但是提升空间有限,因此一些学者尝试将BAS 算法与其他群智能算法结合,综合考虑不同算法的优势与不足并提出混合算法。例如,文献[12]在改进正余弦算法的基础上引入自适应步长的BAS 算法进行二次搜索,取得了优异的寻优精度,但提高了算法复杂度;文献[13]提出一种基于天牛须搜索的花朵授粉算法,在全局搜索阶段引入天牛须寻优加速算法收敛,在低维环境下改善了算法的收敛速度与精度,但是面对高维的寻优问题时算法的有效性有待验证;文献[14]基于模拟退火算法的全局寻优能力将退火过程融入天牛搜索过程,一定程度上提高了算法全局寻优的能力,但是天牛个体仍采用随机搜索策略,寻优精度不高。
针对以上研究的不足之处,本文提出一种基于精英反向学习(Elite Opposition-Based Learning,EOBL)的改进BAS 算法——IBAS,主要从以下两个方面改善算法性能:①采用天牛群搜索代替单个天牛个体,并基于种群的精英个体指导天牛触须的搜索方向;②引入精英反向学习策略,增加种群多样性,增强算法全局寻优的能力。
为确定多港口地区港口投资的均衡,需确定投资人的投资收益函数以及投资策略空间,并模拟港口投资之间的投资博弈行为。
1 标准BAS算法
天牛在寻找配偶或觅食的过程中会使用左右两根长须随机探索周围的区域,任一边的触须感应到更高的目标浓度时,天牛随之移动对应的步长。在寻优问题中,天牛个体朝着适应度更优的一边移动。通过左右两根触须的配合,最终移动至目标位置。假设在d维搜索空间中,天牛个体在第k次迭代的位置表示为左右两须的位置分别表示为:
选取8 个国际通用的基准函数测试算法的有效性,基准函数如表1 所示,其中f1-f4为单峰函数,用于验证算法的收敛速度与寻优精度;f5-f8为多峰函数,侧重于反映算法跳出局部最优的能力。仿真实验环境为MATLAB R2020a,Intel Core i5-9300H CPU,主频2.40GHZ,内存8GB。
mk采用随机生成的方式初始化,计算公式为:
IBAS算法寻优流程如图1所示。
天牛个体的位置更新公式为:
式中,δk为移动步长;sign为符号函数,决定天牛个体的移动方向;f为适应度函数。
两须搜索步长λ与移动步长δk更新公式分别为:
2 IBAS
2.1 种群协作搜索策略
天牛群的位置表示为:
式中,n表示天牛群个数,d表示搜索空间的维度。
从生物医学角度而言,健康管理始终是与医学的进步分不开的。继续研究重要疾病的早期预警机制及对应措施对于健康管理的进步具有促进作用。对于专业从事健康管理的人员来说,积极跟踪最新的医学进展,加强与医院和医生的沟通与联系必不可少。这一方面是健康管理自身的需要。比如,在疾病康复期,健康管理中心可以与医院结合承担躯体与心理康复的部分工作,并完善患者的随访。另一方面,抓住一切机会加强对于医学专业人士的宣教,提高医疗管理人员及医护人员对于健康管理的认识。
式中,∂为[0,1]之间的随机数;xj表示天牛精英个体在第j维的位置信息,xj∈(lj,uj);lj、uj为其在第j维位置最小值与最大值。为保证种群整体进化方向的正确性,采用贪心算法的原则将反向求解后的精英个体位置X'e与原本位置Xe进行适应度比较,最终选取适应度更优的个体位置。
番茄疮痂病与番茄溃疡病症状相似,溃疡病为系统侵染的维管束病害,在果实上呈现“鸡眼状”,叶片上出现白色小枯死斑,引起植株萎焉枯死。据此可区分上述两种病害,防止出现误诊。
式中,ai、bi为基于适应度变化的权重因子。
式中,fl表示为式(1)中Xl对应的适应度值;fbest为当前种群最优适应度。
目前连锁企业在发展过程中,主要的管理模式以统一和集中为主,随着“互联网+”时代的到来,连锁企业要做出适当的调整和改变,与互联网相互结合,形成平台式的管理模式,不仅能够帮助连锁企业有效降低管理成本,而且提高管理质量,增强管理效率。通过“互联网+”的管理模式,可以将用户标签增加至管理平台中,对各个管理项目进行有效的分类,根据属性的不同,还可以创造群组,通过全新的工作管理模式,让连锁企业的组织框架快捷简便,还可以快速找到电话、手机、邮件,支持一键互动,并且还能够同步管理,针对不同的团队和个人共同管理,还有远程培训、视频会议等等多个功能,便捷的操作帮助连锁企业实现更加高效的管理效率。
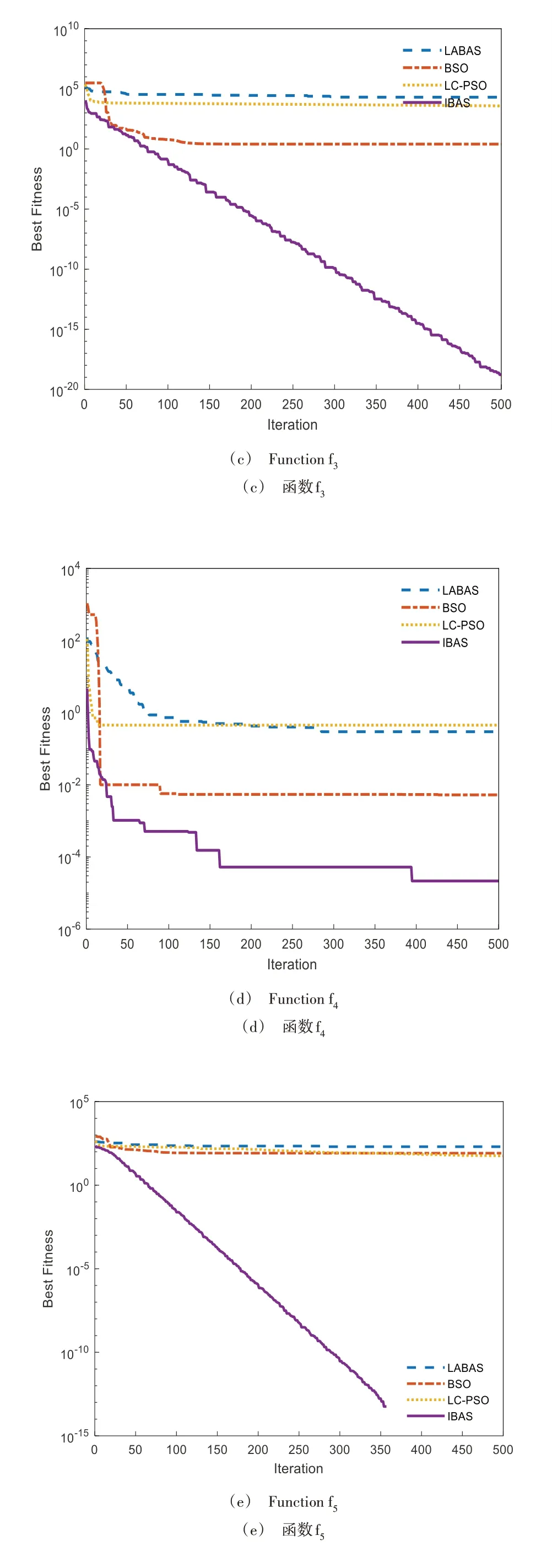
为进一步展示4 种算法的比较情况,图2 给出了各算法在单峰函数f1-f4和多峰函数f5-f8上的适应度变化曲线。由图2(a-d)可知,在针对单峰函数f1-f4的仿真实验中,IBAS 算法的收敛精度随着迭代次数的增加逐渐向理论最优值0 收敛。在函数f1、f3中,IBAS 的收敛速度与收敛精度明显优于其他3 种比较算法;由函数f2可知,其他3 种比较算法在迭代次数25 次后适应度曲线基本保持不变,表明此时算法已陷入局部最优值,而算法缺乏跳出局部最优值的能力,直至迭代次数循环完毕,全局最优解的探索陷入停滞。而由f4可以看出,虽然IBAS 算法在迭代前期的适应度曲线有明显阶梯状的停滞阶段,但适应度曲线在经过一定的迭代次数后均得到进一步改善,表明种群在迭代过程中具有跳出当前局部最优解的能力。
标准BAS 算法中移动步长δ需要根据实际优化问题设定合适的值,且移动后的天牛个体适应度值并不能确保优于前一次迭代。IBAS 算法的天牛位置更新策略省去δ不确定性参数设置问题,且天牛个体位置随迭代次数逐步逼近全局最优值,保证种群整体搜索方向的有效性。初始搜索步长λ0根据实际优化问题决定,本文取λ0=0.5(ub-lb),ub、lb为优化问题的上界与下界。
2.2 引入精英反向学习策略
种群精英个体比其他个体包含更多有效信息,通过构造精英个体的反向解可以增加种群的多样性,扩展种群的搜索范围[16],例如文献[17]将EOBL 策略应用与鲸鱼算法,提高了算法全局寻优的能力;文献[18]针对标准黏菌算法易陷入局部最优、收敛精度低的缺点,采用EOBL 策略提升了种群质量与多样性。天牛种群的精英个体位置定义如式(9)所示,其反向解第j维的计算公式为:
标准BAS 算法中两须的搜索方向由方向标准化向量mk随机决定,具有不确定性,尤其是面对高维复杂寻优问题时并不能正确指引天牛个体的搜索路径。因此,本文引入天牛群搜索机制,将种群精英个体的位置信息应用于天牛个体位置的更新策略,使天牛种群的搜索方向与当前全局最优解相关,有利于提高标准BAS 算法的搜索效率与收敛精度。精英个体为当前种群适应度最优个体,其位置表示为:
2.3 IBAS算法寻优步骤
将IBAS 算法应用于优化问题的步骤如下:①初始化算法参数,包括:种群规模N,迭代总次数T,初始搜索步长λ0;②初始化天牛种群位置,记为{X1,X2,...,XN},计算种群适应度值;③依据适应度大小确定天牛群精英个体Xe;④依据式(15)求解精英个体的反向解X'e,并将精英个体更新为适应度值更优的一方;⑤依据式(1)计算天牛个体向左搜索的位置Xl,并依据式(10)考虑精英个体位置Xe后得出位置X1;⑥依据式(2)计算天牛个体向右搜索的位置Xr,并依据式(11)考虑精英个体位置Xe后得出位置X2;⑦比较两个位置X1与X2的适应度值,天牛个体最终的位置Xnew取值为适应度更优的一方;⑧依据式(6)更新搜索步长λ;⑨更新迭代步数,判断是否达到最大迭代步长T,满足则输出全局最优值,未满足返回步骤3。
资金是企业发展的重中之重。一般来说,工程项目耗资数额大,资金流量巨大。谨慎的管理可以有效控制不必要的资金浪费,从而提高企业竞争力,加强企业的整体实力。因此,资金管理不容忽视。
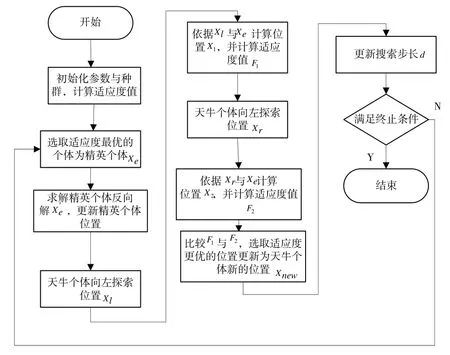
Fig.1 IBAS algorithm optimization flow图 1 IBAS算法寻优流程
3 实验仿真与分析
3.1 基准函数与比较实验
式中,λ为左右两须与天牛个体的距离,对应与两须的搜索步长;mk为方向标准化向量。
为了平衡精英个体指引与左右随机搜索两种策略,引入基于适应度的动态权重,可有效改善算法的收敛速度与精度[15]。IBAS 算法天牛个体左右两须的位置更新策略分别表示为:
为了更好地体现IBAS 算法的优势,选取引入莱维飞行与自适应策略的天牛须算法(LABAS)[19]、社会天牛群算法(BSO)[20]、基于学习与竞争机制的改进PSO 算法(LCPSO)[21]作为比较算法,分别在低维(d=30 维)与高维(d=100 维)进行实验。比较算法在所有实验中均独立测试30次,每次实验迭代次数T均为500 次,种群数量N均为30。记录算法收敛精度的平均值与标准差,平均值反映算法的寻优性能,标准差反映算法的鲁棒性。所有实验中的最优结果加粗显示。为体现比较的公平性,各算法参数均来源于原文献,具体如表2所示。

Table 1 Test functions表1 基准函数

Table 2 Parameter settings of each algorithm表2 各算法参数设置
3.2 低维仿真结果分析
为了验证IBAS 算法的有效性,在维度d=30 维的环境下基于8 个测试函数进行比较试验,4 种算法在f1-f8函数中的性能比较结果如表3所示。可以看出,IBAS 算法在f1-f8中均取得了最佳收敛精度,在多峰函数f8的寻优精度相对较低,但也取得了2.50E+00 的寻优结果,接近理论最优值0。IBAS 算法在多峰函数f5、f7中收敛至理论最优值0,表明IBAS算法具有较强的全局寻优能力。
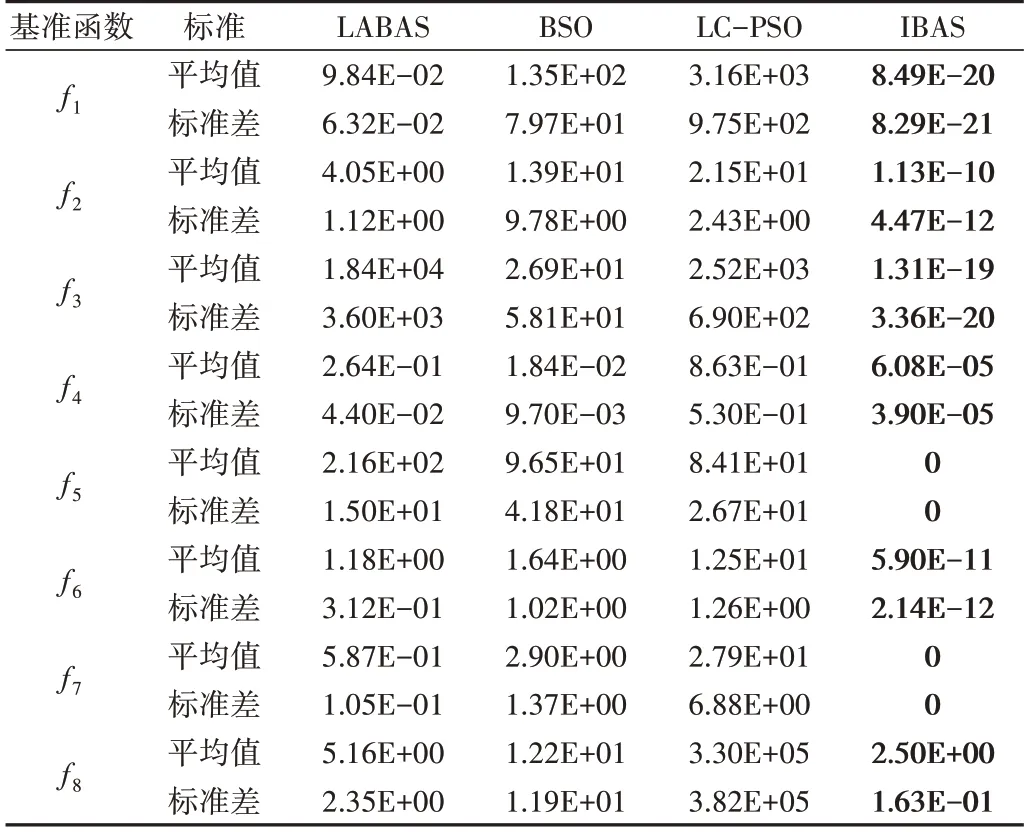
Table 3 Comparison of low dimensional simulation results表3 低维仿真结果比较
在单峰函数f1、f2的实验中,LABAS 算法略优于LCPSO 算法与BSO 算法,在f3、f4中则是BSO 算法取得了较优的寻优精度。IBAS 算法在f1-f4中的寻优精度均明显优于其他算法,表明本文提出的改进策略有效改善了标准BAS算法的寻优精度。IBAS 算法在所有测试函数中均取得最优标准差,表明其具有较强的鲁棒性。
灾害发生后,彝良县龙海乡紧急组织现场救援,下游群众已全部紧急疏散转移。彝良县委、县政府已紧急启动预案,相关部门和救援力量正在赶往龙海途中。
bi计算公式同理,将fl替换为fr,表示天牛个体向右搜索的适应度值。最终通过比较X1与X2对应的适应度值,直接将天牛个体的位置Xnew更新为适应度值更优的一方,计算公式为:
综上所述,3 种比较算法在迭代初期适应度曲线便陷入停滞状态,算法收敛精度不理想,而IBAS 算法表现出了最优秀的寻优性能。
在多峰函数f5-f8上的测试对于算法全局寻优能力的要求更高。由图2(e-h)可知,对于函数f5、f6、f7,3 种比较算法在迭代初期种群便陷入停滞状态,适应度曲线几乎保持水平,不再进一步延伸。而IBAS 算法在函数f5、f7上收敛至理论最优值0,BSO 与LABAS 算法仅在函数f8上的收敛精度接近于IBAS 算法,表明IBAS 算法具有优秀的全局寻优能力。
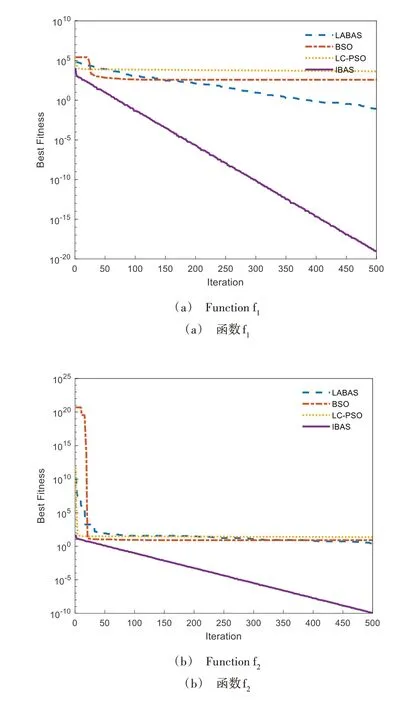
Fig.2 Comparison of fitness curves of algorithms under low-dimensional testing图2 低维测试算法适应度曲线比较
3.3 高维仿真结果分析
为进一步验证IBAS 算法的全局寻优能力,分析其在高维复杂寻优问题的有效性。基于8 个基准函数,在维度d=100 维下进行仿真比较实验,结果如表4 所示。可以看出,与30 维的实验相同,IBAS 算法在所有测试函数中均取得了最佳收敛精度平均值与标准差。LABAS 算法在30 维下单峰函数f1中的收敛精度为9.84E-02,在d=100 维下的收敛精度变为4.67E+04;在函数f8中,30 维下的收敛精度为5.16E+00,而在100 维下变为4.23E+08,寻优精度下降的现象在其他测试函数中均有不同程度的体现,对于BSO算法的分析也可得出相同结论。相反地,LC-PSO 算法在高维下的寻优性能得到一定程度的提升,在多峰函数f8中,其30 维下的寻优精度仅为3.30E+05,在100 维下为6.82E+01,仅次于IBAS 算法,表明LC-PSO 算法更适合高维寻优问题。而IBAS 算法无论在低维还是高维实验环境下均表现出最优寻优性能,且在高维条件下,IBAS 算法在单峰函数与多峰函数中的寻优精度依然保持稳定。
2)组合惯导航向角精度测试试验。为了验证组合惯导对掘进机航向角的测试精度,将组合惯导固定在如图8所示的定位精度为0.02°的三轴转台上,通过三轴转台转动模拟掘进机机身航向角的变化。试验过程中,通过三轴转台控制软件设置三轴转台转动到从0°间隔5°到20°,再从20°间隔5°到0°,每个角度测试10次取平均,得到航向角测试结果见表5,根据表5可知航向角测试误差在0.2°范围内。
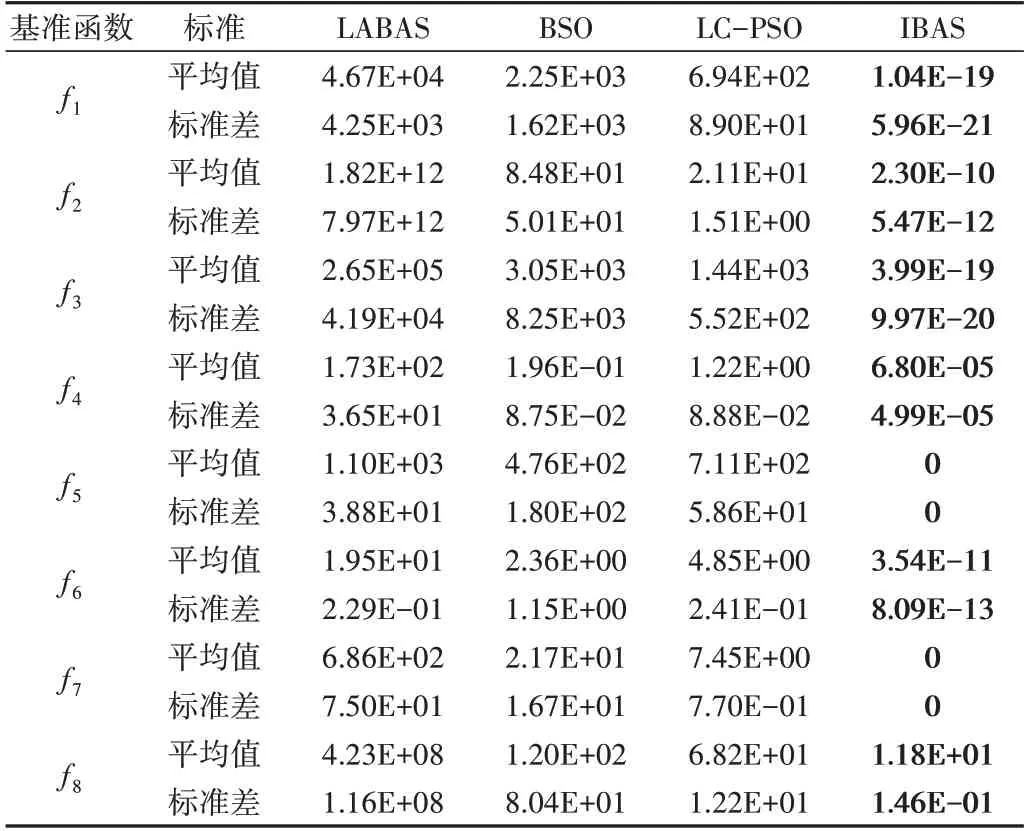
Table 4 Comparison of high dimensional simulation results表4 高维仿真结果比较
图3 为高维情况下各算法在f1、f8函数中的适应度曲线比较。可以看出,在高维条件下,对于单峰函数f1,LABAS算法适应度曲线几乎保持水平,表明在高维搜索空间中其全局寻优能力较差,而IBAS 算法依然保持较优的收敛速度与精度。对于多峰函数f8,LABAS 算法收敛精度下降明显,而IBAS算法取得了最优收敛精度。
(4)环境污染:矿山尾矿严重破坏了土壤、植物、大气和水源等周边生态环境,矿区及周边区域空气粉尘飞扬,植物枯黄,土地沙漠化,水源酸化,并伴随刺激性气味,生态环境遭到严重破坏。尾矿中的硫化物、重金属离子、药剂等物质常常具有一定毒性,而且这些物质之间的相互作用会加剧对周边水源、土壤以及地下水的污染,并随河流迁移影响更大区域的生态环境。目前,我国因尾矿直接和间接污染土地面积超过1 000余万亩[22]。
在纤溶酶的作用下,tPA单链分子的敏感肽键Arg275-Ile276很容易被水解,单链随即断裂成2条链形式,形成双链tPA。双链分子的A链(又称H链或重链,1~275位氨基酸)位于分子N端,B链(又称L链或轻链,276~527位氨基酸)位于分子C端,2条链之间由1个二硫键连接。其中A链为tPA与纤维蛋白结合所必须;B链包含活性位点,对底物纤溶酶原具有高度特异性的活化作用[24]。电镜下tPA单链和双链的形状很难分辨,它们都是相对紧致的椭圆形,其长轴和短轴分别约为13 nm和10 nm,几个功能区极小并折叠在分子内部,分子整体看起来类似球状[25]。
综上所述,IBAS 算法具有优秀的全局寻优能力,面对高维复杂优化问题时仍较为有效。
4 结语
本文针对标准BAS 算法寻优精度不高,面对高维复杂寻优问题时极易陷入局部最优的问题,提出一种基于精英反向学习的IBAS 算法。该算法将天牛个体改进为天牛种群,将种群的精英个体引入天牛左右两须的搜索策略,提高了搜索效率;同时采用精英反向学习策略增加种群多样性,增强了算法的全局寻优能力。在8 个基准函数上的仿真实验结果表明,IBAS 算法展现出优秀的寻优精度与鲁棒性,在面对高维寻优问题时依然保持优秀的寻优性能,验证了本文提出的2 种改进策略的有效性。然而本文并未考虑IBAS 算法在实际工程问题中的应用,可作为下一步研究方向。

