AB双层磁性薄膜的界面自旋波

邱荣科, 张欣荣, 刘忠菊

(沈阳工业大学 理学院, 沈阳 110870)

随着信息产业在生产生活、航空航天、国防安全等领域的快速发展,研制出以半导体材料为基础的具有可靠性高、功耗低、集成度高等优点的集成电路系统迫在眉睫,直到2004年Andre Geim和Kostya Novoselov采用机械剥离法从石墨材料剥离出具有低维特性二维材料石墨烯[1],人们才将目光转向了二维材料(纳米薄膜、超晶格等),并发现薄膜材料可以应用于信息处理与存储以及自旋器件等领域.磁性薄膜的巨磁电阻效应、巨霍尔效应等特性应用较为广泛.基于磁性薄膜的巨磁电阻效应可以制备出具有高信噪比、高灵敏度、高存取速度的GMR磁头.

磁性材料中电子的自旋磁矩将围绕其在外场中的平衡位置进行旋转,并产生铁磁共振频率.如果自旋序列并非单一形式,则会产生集体运动并在铁磁中传播形成自旋波[2].自旋波传输、存储和处理信息是通过将信息编码到电子自旋角动量而非电子电荷中,因而可以更快地处理数据,同时降低能量耗散.磁性薄膜自旋波的性质对逻辑器件、色散滤波器、自旋电子学器件性能的提高起着重要作用[3].近年来,科研工作者对磁性薄膜自旋波性质进行了大量实验研究,其中以铁磁共振[4-7]、光散射[8]、电子能量损失谱[9]等手段为主,如Rajeswari[9]采用电子能量损失谱法检测到Co/Ni和Co/Cu双层膜界面自旋波的直接信息.在理论分析中常采用线性自旋波近似方法[10]、格林函数方法[11]、哈密顿对角化方法[12]、界面重标化方法[13]等对磁性薄膜中自旋波的性质进行了研究.邱荣科等[11]研究了铁磁性薄膜中表面自旋波频率受不同因素的影响规律;Yun等[13]分析了界面自旋波存在的充分必要条件.由于界面可以诱发许多磁性物理现象,如界面感应磁化反转效应、超快磁化过程中的界面效应等[14],可对提高一些基于磁性多层膜技术的现代信息设备性能具有至关重要的作用.鉴于自旋波和多层膜的界面效应的重要性,研究非对称双层膜界面自旋波的性质具有重要意义.

1 模型与计算

非对称双层磁性薄膜结构如图1所示.图1a为非对称性AB双层磁性薄膜模型;图1b为AB双层磁性薄膜原子层示意图;图1c为单层原子层的x-y平面结构图;图1d为二维布里渊区.

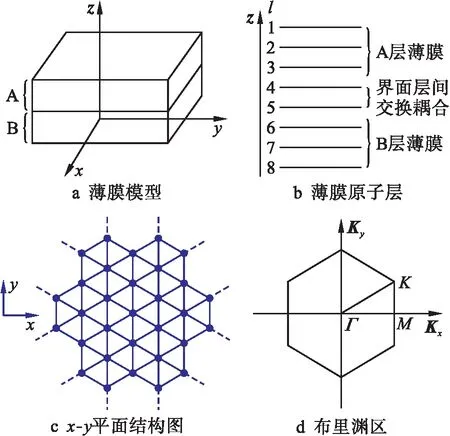
图1 非对称双层磁性薄膜结构

以海森堡模型为基础,研究外部物理因素和界面参数对非对称双层磁性薄膜中界面自旋波性质的影响.本文采用的哈密顿量和计算方法与文献[15]相似.

非对称双层磁性薄膜的哈密顿量可以表示为

(1)

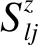
最初自旋方向沿z轴正方向,外磁场方向与自旋初始方向相同.为了分析非对称双层磁性薄膜中界面自旋波的性质,引入格林函数,即

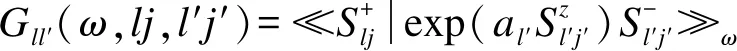
(2)

式中:S+和S-分别为自旋产生和湮灭算符;a为常数;ω为自旋波频率.

建立格林函数运动方程时利用Tyablikov退耦近似和Anderson-Callen退耦近似分别处理交换耦合项和单格点各向异性项.模型中第4、5原子层为界面层.令JAB为第4、5原子层的层间交换耦合系数;Jint为第4、5原子层的层内交换耦合系数;Dint为第4、5原子层的界面各向异性参数.设A层自旋量子数SA为1,B层自旋量子数SB=1.5.为了计算简便,将薄膜内体交换耦合系数设为1,且将其作为其他物理量的约化单位.将薄膜内部原子的体各向异性参数设为零,故只考虑薄膜界面原子的各向异性参数.本文重点研究各物理参数对非对称性AB双层磁性薄膜界面自旋波在布里渊区内占有面积的影响.

2 计算结果分析

图2为非对称性AB双层磁性薄膜在二维布里渊区内频率随波矢的变化情况.8支自旋波谱按照能量由小到大排列分别表示为ω1,ω2,…,ω8.在布里渊区Γ-M和K-Γ中,自旋波频率随波矢的增加而增加,但ω1、ω2、ω3和ω4的上升趋势较慢,ω5、ω6、ω7和ω8的上升趋势比较迅速.在平面布里渊区M-K中所有自旋波谱均随着波矢的增加而缓慢增加.因为A和B层的自旋量子数具有非对称性,自旋波在双层膜中的分布如图3所示.图3中ρ/ρ0为约化态密度,ρ为不同频率下自旋波的态密度值,ρ0为在M点处磁性薄膜界面层(第5原子层)中界面自旋波的态密度值.SA、SB、B0、JAB、Jint、Dint和τ的数值设定与图2相同.

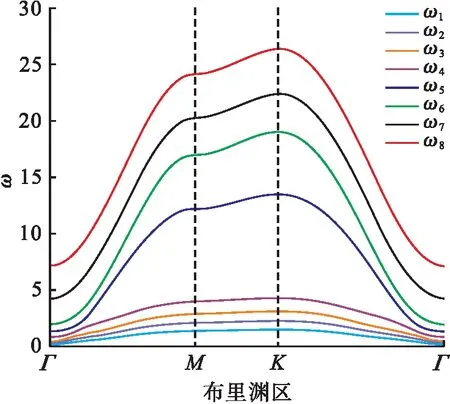
图2 非对称磁性薄膜的自旋波谱

图3 不同波矢的自旋波分布

所以在自旋波谱中不存在简并现象.计算中各项参数取值如下:SA=1.0,SB=1.5,B0=0.15,JAB=0.65,Jint=0.75,Dint=0,约化温度τ=T/Tc=0.5(T为温度,Tc为上述参数下的居里温度).

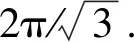
图4为温度对界面自旋波在平面布里渊区中占有面积的影响.第4、5原子层界面自旋波在平面布里渊区中的占有面积分别用红色和蓝色阴影表示(图5～8阴影颜色设定相同).界面自旋波占有面积的边界对应于临界波矢量.计算中SA=1.0,SB=1.5,B0=0.15,JAB=0.65,Jint=0.75,Dint=0,τ为0.45、0.5、0.7和0.8.当τ=0.45时,只有第5原子层界面存在界面自旋波ω5.随着τ的增大,第4原子层界面中出现了界面自旋波ω4.两个界面层的界面自旋波在布里渊区中占有面积的变化规律均为先增大后减小.当τ=0.8时,只有第5原子层界面存在界面自旋波ω5,第4原子层界面的界面自旋波ω4消失.可见,第4原子层界面自旋波存在于中温区间,第5原子层界面自旋波存在于全温区间.

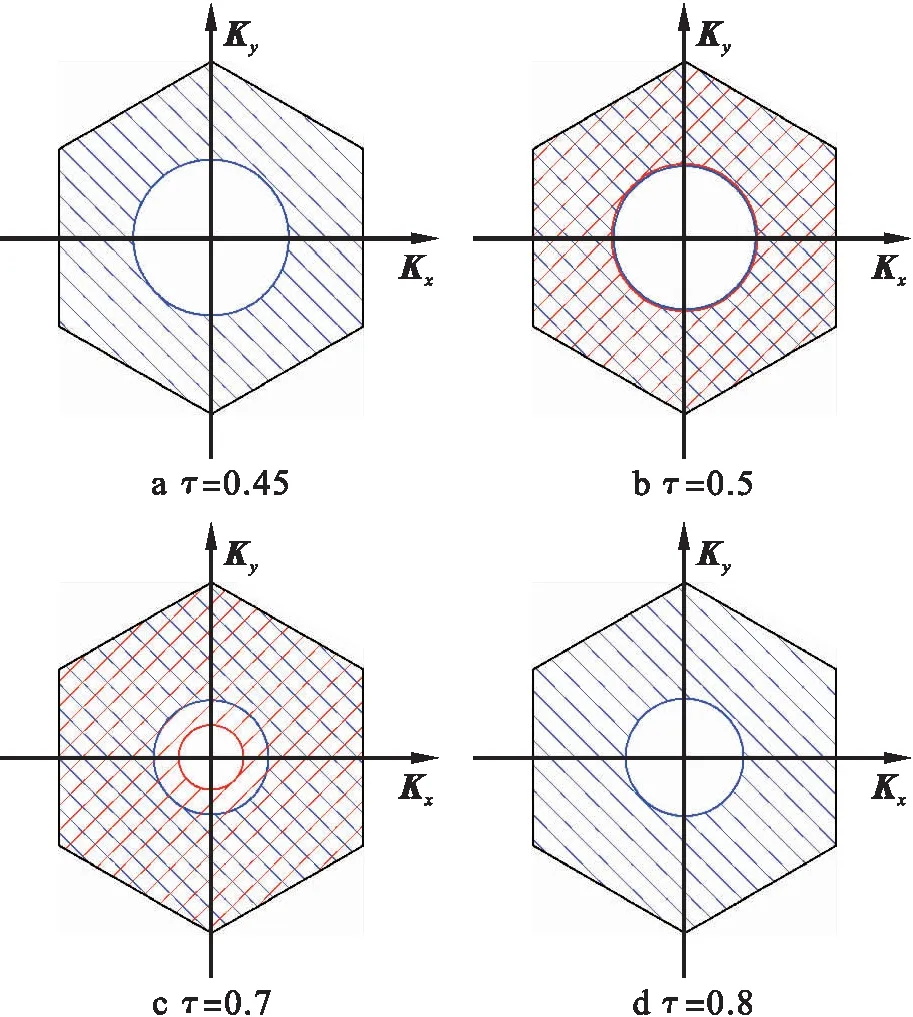
图4 温度对布里渊区中界面自旋波的影响

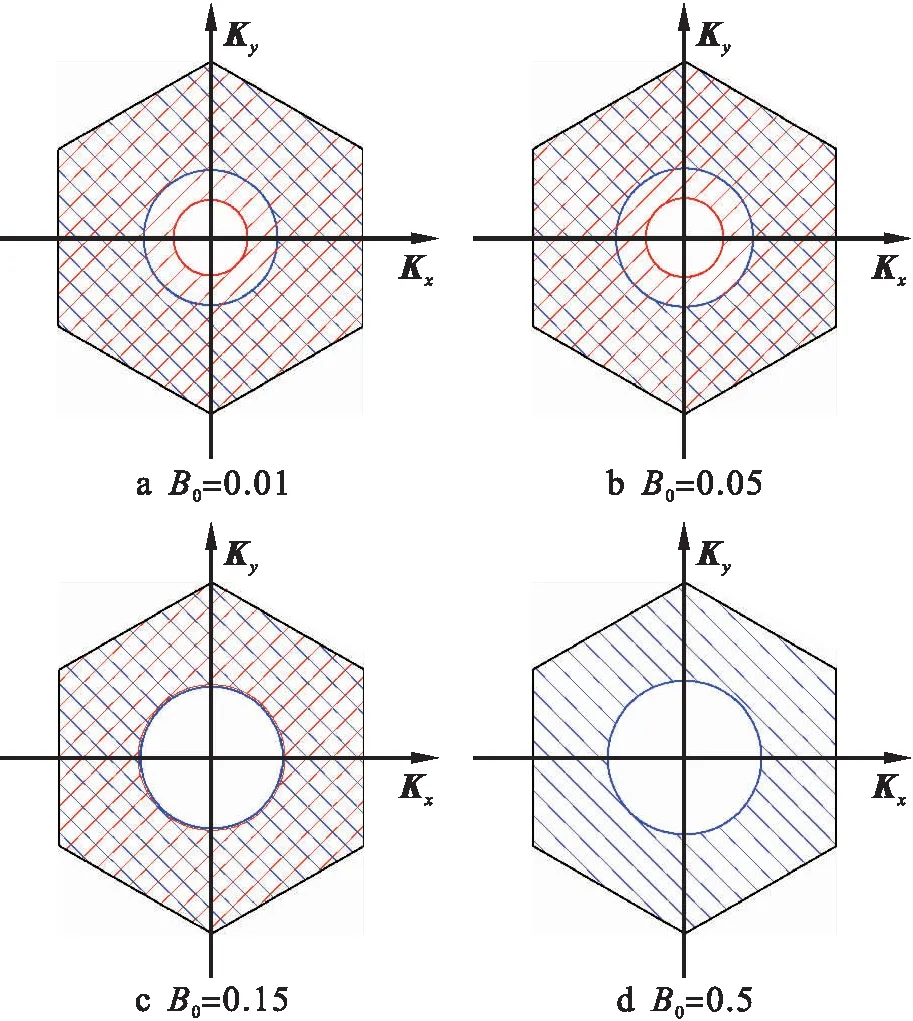
图5 外磁场对布里渊区中界面自旋波的影响

图5为外磁场对界面自旋波在布里渊区中占有面积的影响.计算中SA=1.0,SB=1.5,τ=0.5,JAB=0.65,Jint=0.75,Dint=0,B0为0.01、0.05、0.15和0.5.由图5可知,随着外磁场的增大,两个界面层的界面自旋波在布里渊区的占有区间面积减小,当B0=0.5时,只有第5原子层界面存在界面自旋波ω5,第4原子层界面的界面自旋波ω4消失.

图6为界面自旋波在布里渊区中占有面积受界面层间交换耦合系数的影响规律.计算中SA=1.0,SB=1.5,τ=0.5,B0=0.15,Jint=0.75,Dint=0,JAB为0.3、0.65、0.75和0.9.由图6可知,当JAB=0.3时,只有第5原子层界面存在界面自旋波ω5.随着界面层间交换耦合系数的增大,第4原子层界面出现了界面自旋波ω4,且第4原子层界面自旋波ω4在布里渊区中的占有面积逐渐增加,而第5原子层界面自旋波ω5在布里渊区中的占有面积逐渐减小.

图6 界面层间交换耦合对布里渊区中界面自旋波的影响

图7为界面自旋波在布里渊区中占有面积受界面层内交换耦合的影响规律.计算中SA=1.0,SB=1.5,τ=0.5,B0=0.15,JAB=0.65,Dint=0,Jint为0.5、0.75、0.8和0.9.由图7可知,当Jint=0.5时,只有第5原子层界面存在界面自旋波ω5.随着界面层内交换耦合系数的增大,第4层界面也出现了界面自旋波ω4,且第4原子层界面自旋波在布里渊区中的占有面积逐渐增加,第5原子层界面自旋波在布里渊区中的占有面积逐渐减小.

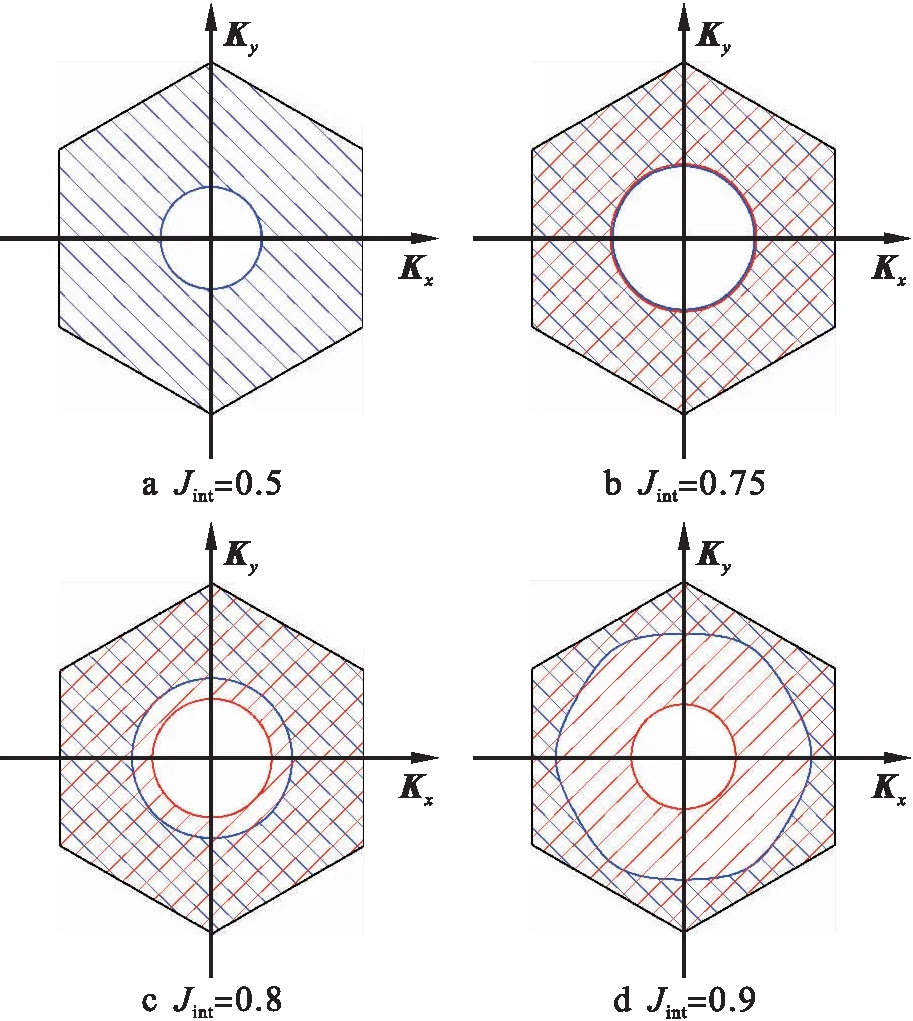
图7 界面层内交换耦合对布里渊区中界面自旋波的影响

图8为界面自旋波在布里渊区中占有面积受界面各向异性的影响规律.计算中SA=1.0,SB=1.5,τ=0.5,B0=0.15,JAB=0.65,Jint=0.75,Dint为-0.3、0、0.1和0.3.由图8可知,当Dint=-0.3时,两个界面层均存在界面自旋波ω4和ω5.随着界面各向异性参数的增大,第4原子层界面自旋波在布里渊区中的占有面积逐渐增加,第5原子层界面自旋波在布里渊区中的占有面积逐渐减小.但第4原子层界面自旋波在布里渊区中占有面积增加得较为明显,第5原子层界面自旋波在布里渊区中占有面积减小幅度较小.

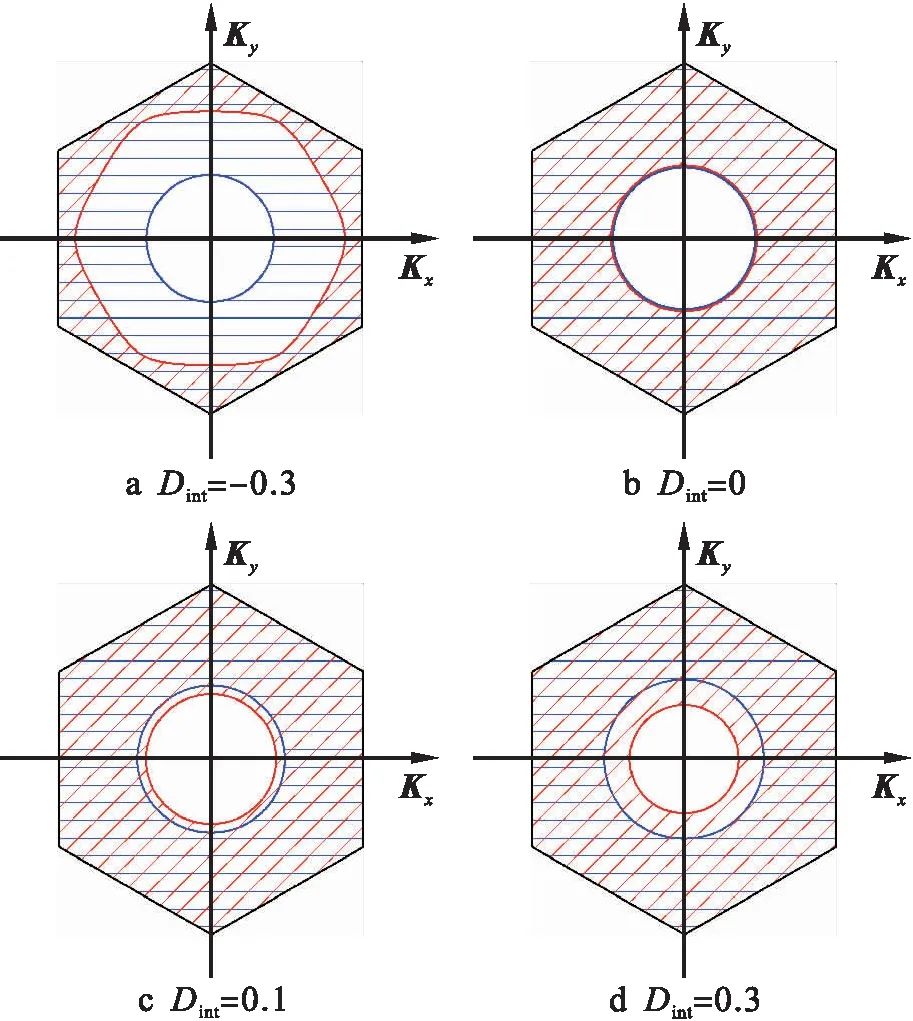
图8 界面各向异性对布里渊区中的界面自旋波的影响

3 结 论

通过构建非对称AB双层磁性薄膜的结构模型研究了各项物理参数对界面自旋波在平面布里渊区中占有面积的影响.结果表明:随着温度的升高,界面自旋波在布里渊区中的占有面积先增大后减小,且第4原子层界面自旋波存在于中温区间,第5原子层界面自旋波存在于全温区间.随着外磁场强度的升高,界面自旋波占有面积减小.随着界面层间和界面层内交换耦合的增大,第4原子层界面自旋波在布里渊区中的占有面积逐渐增加,第5原子层界面自旋波在布里渊区中的占有面积逐渐减小,且当界面层间和界面层内交换耦合较小时,只存在一个界面自旋波ω5.随着界面各向异性的增大,第4原子层界面自旋波在布里渊区中的占有面积逐渐增加,第5原子层界面自旋波在布里渊区中的占有面积逐渐减小.界面自旋波趋于出现在大波矢区域,即易出现短波长界面自旋波,界面自旋波在二维布里渊区占有面积的增大,意味着短波长界面自旋波和长波长界面自旋波有可能出现,这为进一步设计基于磁性多层薄膜的微波器件提供了理论基础.