三角形结构的篱笆为什么稳定？

辛诺佳

［摘 要］主问题是学生学习存在困惑的知识点，也是引发学生思考、开展结构化学习的重要途径之一。以 “三角形结构的篱笆为什么稳定？”为主问题探究三角形，创设串联教学的多个环节，引导学生自主探究，让学生全面认识三角形。

［关键词］三角形；主问题；稳定性

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）08-0065-03

在主问题引导的课堂中，教学更关注问题带来的思维碰撞，更关心学生思维能力的发展，以实现学生思考、表达、提问等多维度数学素养的全方位发展。主问题是一节课的灵魂，是结构化教学的着眼点，是资源构建的整合点，也是有效教学的开展点。下面笔者就以“认识三角形”一课为例，  浅谈如何简化教学结构，精炼教学内容，从而实现数学课堂的精简、集约。

一、分析学情，确定主问题

“认识三角形”一课是苏教版教材四年级下册“三角形、平行四边形和梯形”中的内容。这部分内容旨在让学生联系已有的知识经验，通过观察、操作、测量等学习活动，初步认识三角形。

“认识三角形”是本单元的起始课，在这一课中建立正确的表象和获得丰富的活动经验，对之后学生学习“三角形的三边关系”“三角形的内角和”至关重要。如何以一条明确的主线串联起这些知识点，进而有条理、 结构化地呈现知识点，是教师需要思考的问题。仔细分析教材后，笔者认为以“三角形结构的篱笆为什么稳定？”为切入点，既能让学生深入地掌握本节课的知识，又能以此作为后两节课的探究主线，还能引导学生从不同角度解读三角形的稳定性，形成体系化的知识框架，让学习真实发生。

二、环环相扣，探究主问题

1.情境设疑，引出主问题

师：我们常说数学源于生活，今天我们的课堂就从生活中发生的一件小事开始。（呈现动画）李叔叔花园的篱笆总是左右倾斜，很不稳定，后来他想到了一个办法，只用一根木条，便使篱笆不再左右倾斜（如图1）。

师：你们相信一根木条有这么大的作用吗？口说无凭，不妨做一个简单的实验验证一下。

（出示四边形教具，请学生上台拉一拉，感受四边形的不稳定性）

師：你们拉的感受是什么？

生1：四边形很不稳定。

师：是呀，仔细观察这个四边形的每个角，轻轻一拉，每个角的大小都随之变化，看来这样的结构确实不太稳定。

师：谁来做小木匠，让它稳定下来？

（学生尝试在四边形的对角线上绑一根小棒）

师：你加了一根小棒，四边形一下子就稳定了，怎么会这么神奇啊？

生 2：因为加了这根小棒后，四边形每个角的大小都被固定住了，所以图形就稳定了。

生 3：是因为出现了三角形。

师：是啊，正好变成了2个三角形。篱笆的形状原来是四边形，后来变成了2个三角形，看来它之所以稳定，是因为有三角形。三角形结构的篱笆为什么稳定呢？

【评析】本节课通过李叔叔修篱笆这一情境，让学生观看修篱笆的过程、拉动四边形教具，直观感受三角形的稳定性，从而引发疑问：出现三角形结构后，篱笆为什么会变得稳定？要解决这个问题，学生就必须思考三角形有哪些特征，是什么决定了它的稳定性。学起于思，思源于疑，在主问题的引导下，学生的思维始终处于积极、主动的状态，自然而然推动学习的发生。

2.观察比较，分析主问题

师（出示一些三角形，图略）：观察这些三角形，有什么相同的地方？

生1：它们都有 3 条边。

师：其他三角形也有3条边吗？

生1：是的，每个三角形都有3条边。

师： 还有不同的发现吗？

生2：三角形有3个顶点、 3 个角。

师：看来三角形的特征与“3”有关，对此，你想提出什么问题？

生3：三角形的稳定性是否与3 条边、3 个顶点有关？

师：这个问题有意思！三角形的稳定性到底是和 3 条边有关，还是和 3 个顶点有关，让我们继续探究。

【评析】伴随着对主问题的思考，学生初步探究了三角形的特征，发现“三角形有3个角、3条边、3个顶点”。在此基础上，学生再次产生疑问：三角形的稳定性到底和哪一个特征有关？顺着这样的思路，学生的探究将更有方向感。

3.追本溯源，聚焦主问题

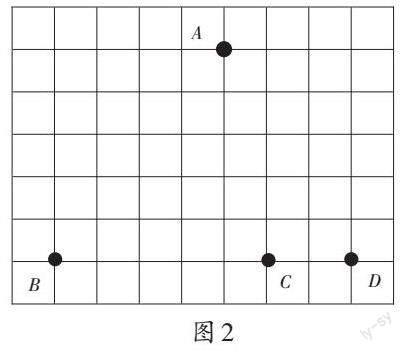
师：那我们先从点开始研究，如图2所示，这里有A、B、C、D 4个点，任选其中3个点做顶点，连一个三角形，你有什么发现？

生 1：点的位置不同，画出的三角形也不同。

师：固定3个顶点的位置，就能确定三角形的形状。为什么没人选 B、C、D这3个点呢？

生2：这3个点连起来是一条线段，不是三角形。

（小结：三角形的3个顶点不能在同一条直线上）

师：注意看！现在将点C向上移1格，这样可以画出一个三角形吗？如果继续向上移1格呢？在移动过程中，你感觉三角形有什么变化？

生3：三角形的边变长了。

生 4：我感觉三角形越来越高。

师：想一想，三角形为什么会越来越高？

生5：点C变高后，拉动三角形变高。

师：为了看清楚，我把点C的运动轨迹画出来。点C越高，三角形就被拉得越高。看来，三角形是有高度的，它可以从一个“矮胖子”变成一个“高瘦子”（如图 3）。

（教师用课件隐去 BC、DC 2条边，如图4）

师：你们从图中发现了什么？

生6：点C的运动轨迹是它到对边的垂线。

师：生6提到了一个很关键的词——垂线！能进一步说说你这句话的意思吗？

生6：点C向上移动的时候是平移运动，始终和 BD 边垂直，就相当于我们学的画垂线。

师：原来是我们的“老朋友”，那垂线可以传递给我们什么信息？

生 7：垂线能表示点到直线的距离。

生 8：这条线段是几厘米，三角形的高就是几厘米。

（教师用课件恢复 BC、DC2条边）

师：现在加上这样2条垂线，你觉得这3条垂线哪一条可以表示这个三角形的高（如图5）？

生9：从点C到对边的这条垂线。

师：他说的对吗？我们来看看课本上是怎么描述三角形的高的。

师（旋转图5中的三角形）：旋转这个三角形，这条线段还是三角形的高吗？

生10：是。

师：如果再次旋转这个三角形呢？

生10：依然是。

师：为什么无论怎么旋转，这条线段始终都是三角形的高？

生11：因为不管三角形怎么变，这条线段都是从顶点到底边的垂直线段，这样的线段就是三角形的高。

师：生11解释得真到位！看来高始终“坐”在底边上。有底就有高，有高就有底！

【评析】在本环节中，笔者先让学生通过画一画，明确“不在同一条直线上的3个点能确定唯一的三角形”。接着向上移动其中一个顶点，让学生直观感受移动轨迹的长短决定三角形的高度，而高度一旦确定，三角形的形状便也随之固定。然后笔者适时揭晓这样的垂直线段就是三角形的高，使高的概念从抽象变得清晰直观。最后通过旋转三角形，让学生辨别高是否有变化，以此深化学生对高的理解。

在以上环节中，主问题引导学生从研究特征聚焦到研究点，接着逐步深入问题本质，明确指向三角形的高，感受“三角形的高就是表征三角形高度的量”，追本溯源，让图形变得“有血有肉”。这时，学生对三角形特征的概念构建，开始从散乱走向规整、从模糊走向清晰，逐渐形成完备的整体认知结构。

4.实践操作，深究主问题

师：想不想自己动手画一画三角形的高？

（展示学生3种不同的高的画法，如图 6）

师：这些都是这个三角形的高吗？

生1：是的，它们都是从顶点到对边的垂线。

师：为什么同一个三角形却有3条不同的高？

生2：因为是从不同的顶点引出的。

生3：因为底边不同，所以高也不同。

师：看来三角形的底和高是一一對应的，不同的底对应不同的顶点，也就有不同的高，那么三角形到底有几条高？

生（齐）：3 条！

师：要是把 3 条高都画出来，会发生什么呢？

生4：3条高交于一点。

师：观察图形（如图7），你有什么发现？

生5：每一条高都连接一个对应的顶点，高的长度决定了顶点的位置，也决定了三角形的形状。

师：生5说得太棒了，这3条高就是稳稳撑起三角形的3条支架。

【评析】随着研究的深入，学生在实践操作中发现“三角形有3条高，且高与底存在对应关系”。出示图7，让学生产生更深层的感悟：3条高就像支架一样，决定了三角形的形状，因此三角形不易变形。至此，贯穿全课的主问题得以顺利解决。

5.启发思考，延伸主问题

师：同学们，你们真是太了不起了，在李叔叔修篱笆的故事中发现问题，着手研究三角形的特征，聚焦“顶点”，又顺着思路将研究指向“高”，最终发现三角形的稳定性与“高”有关。那么，三角形的稳定性是不是只和“高”有关呢？

生 1：也许和三角形的边也有关。

生 2：还有可能与角有关。

师：这些想法不错，下一节课我们就从“边”的角度继续探究三角形的稳定性！

【评析】本节课虽已结束，但对主问题的探究并未停止。在第二课时中，学生将仍以“三角形的稳定性”为主线，从另一个角度——边进行思考，理解三角形的三边关系。由同一个主问题生发“三角形”“高”“三边关系”等概念，形成一个更为开放、循环、流动的知识体系，让教学更有结构性，让学习更深入。

综上所述，在本节课中，主问题的设立让学生知道了原有的知识无法解答新的疑问，迫使学生打破思维闭环，从研究三角形的特征开始层层推进、由表及里地认识高、了解高。不难看出，由主问题统领的课堂，教学推进路径与学生思考路径相契合。解决主问题的过程，也是学生重建三角形认知的过程。而主问题的设立也使学习逐步深入，让学习真实有效地发生。

（责编 覃小慧）