小学数学深度教学应“深”在何处？

摘要：在“双减”及新一轮课程改革背景下，针对小学数学学科教学现状中的浅层学习问题，依据数学学科教学特点，在深度教学理论指导下，在教学中落实深度教学，提出指向数学本质的“深”问题，从浅认知转向真探究；组织多形式“深”互動，从知识取向转向素养取向；激发内在“深”动力，从教师立场转向学生立场。

关键词：深度教学；数学本质；学科素养；学生立场

中图分类号：G623.5 文献标志码：A 文章编号：1673-9094（2023）07-0074-05

减负的本质在于增效，如何提升课堂教学质量，是所有一线教师关注的焦点和亟待解决的困惑。虽然经历了多年课堂教学改革，小学数学课堂仍普遍存在着以下“浅”的现状：一是认知浅层，对数学本质的理解不足；二是知识取向，缺乏数学思想方法的揭示；三是学习过程被动，课堂沉闷无生机。这些浅层学习的表现直接影响着数学教学高效能目标的达成，与以素养培养为目标的课程改革方向相背离。深度教学理念倡导以学生为中心，被广大教师所关注。然而，如何在小学数学课堂教学中落实深度教学？小学数学深度教学应深在何处？以下从三个角度的“深”对该问题进行探讨，以求真正实现减负增质。

一、提出指向数学本质的“深”问题，从浅认知转向真探究

《义务教育数学课程标准（2022版）》中多处强调数学本质，深度学习也强调基于理解的学习[1]，反对将知识“窄化”，实现理解学科本质的目的。在课堂中开展真正意义的探究性学习，正是促进学生在观察、对比、发现、验证中形成可理解的学习方式，它能帮助学生从直观走向抽象，从现象走向原理。反观当下的数学课堂，教师借以引发学生探究的许多问题，常常只关注了教材中例题表面的“浅问题”，未能提出有效引导学生挖掘现象背后指向数学本质的“深”问题，因此学生所经历的探究过程也常常是缺乏认知含量的“假探究”，难以对数学本质有深刻的理解。为解决这一问题，我们须设计课堂中的“深”问题，帮助学生由表及里，做指向数学本质的真探究。那么数学课堂中的“深”问题应具有哪些特点呢？

（一）问题应指向数学内在逻辑关系

数学是研究空间形式和数量关系的科学，而这也正是数学本质的体现，是所有数学概念和原理的内在逻辑。这些内在逻辑隐藏在具体表象的背后，教师只有在教学中提出指向数学内在逻辑关系的问题，才能引导学生的探究活动由表及里，进而发现深层的数量关系及数学规律，将认知引向深处。

例如，在学习“长方体的认识”一课时，教师往往认为学生能正确摸出长方体的面、棱、顶点，就是理解了“面”“棱”“顶点”的概念。然而教材是这样描述的：“棱”——面和面相交的线段，“顶点”——棱和棱的交点。也就是说，对“棱”的理解只停留在能摸出来还远远不够，它必须建立在对面与面之间的关系和相交的结果的认知基础上，这就是概念的内在逻辑。一旦脱离对面的研究，就不能深刻理解棱的概念。顶点亦然。为此我们设计了这样的提问：“哪个面和哪个面相交成哪条棱？哪条棱和哪条棱相交成哪个顶点？”这个问题看似简单，却将学生的认知聚焦在了“关系”上，通过面与面的关系认识“棱”，通过棱与棱的关系认识“顶点”。在这一问题的激发下，学生不再停留在“摸”的认知层面，而是仔细观察、思考，再用数学语言表达：“上面和前面相交成一条水平的棱，前面和左侧面相交成一条打竖的棱……”随后学生指着不同的三条棱相交的位置解释顶点，实现对两个几何概念的深层理解。

（二）问题的解决须借助高阶思维的参与

对于学习者而言，低阶思维往往使其停留在对事物表面的感知，然而数学本质的抽象性决定了高阶思维在学习中发挥重要的作用。学生的探究过程是否需要高阶思维的参与，取决于教师所提问题的质量。如果问题只要求学生把看到的读出来、记下来，这样的思维水平只会让学生的学习停留在知识的表层；如果问题的解决需要学生经历分析、综合、评价和创造等高阶思维过程，需要比较异同、有依据地证明、综合归纳，那么就能帮助学生实现对知识本质的深层理解。

如人教版五年级上册“位置”单元的例2，表面上只是让学生在方格图中学会用数对表示位置，而学生很轻易就能读出指定位置的数对。然而这一步的思维水平较低，认知还很表浅，数对的内在特点并未被发现。这就需要教师创设更具启发性的问题，激发学生往数对更本质的特点探究。我们提出了以下问题：“是不是所有的数对都能找到它的位置？是不是所有的位置都能用数对表示？”围绕这两个问题，学生将目光从例题中的“有限”拓展到“无限”，并引发了激烈的辩论，最终凭借想象超越了眼前可见的范围，再通过综合分析（0，0）的作用以及方格图中行与列的特点、点与格的对应关系，更深刻地理解了数对的本质特征。这个问题有效调动了学生的高阶思维，帮助学生探究现象背后蕴含的内在原理。

（三）立足单元、学段、学科知识组块设计问题链

数学课程内容中的四大领域，以主题的形式分布在不同的学段、学期、单元、课时中。知识间存在着严密的内在联系，且螺旋上升。孤立的知识难以建立起观念系统[2]128，而以往教师却习惯着眼于课时的某个知识点，问题设计也仅限于本节课的内容。这样设计问题必然缺乏了连贯性和整体性，降低课堂提问应有的效能。教师应站在知识发展的视角上，在不增加学习难度的前提下加强问题间的关联性，并在单元甚至学段、学科的高度上设计出系列进阶性的问题链，激发学生真实的深层思考。

如关于分数的学习，三年级教材安排了一个单元学习“分数的初步认识”，而到五年级将继续学习分数的意义和相关性质。虽然认知水平不同，但两段学习存在着密切的联系，教师也应把握契机向学生做适当的渗透。在三年级学习“分数的初步认识”中，教师设计了这样的问题链：

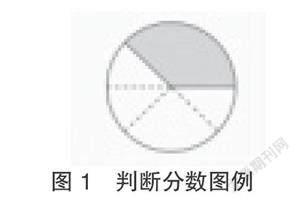
问题1.图1中的阴影部分能否用   表示？

问题2.如果增加虚线，阴影部分能用哪个分数表示？

问题3.你发现了什么规律？

这三个问题组成了既立足于本单元对分数的初步理解，又体现知识发展的问题链。在第一个问题中，学生根据分数的由来和分子、分母的含义，较易判断出涂色部分显然不能用

表示。在第二个进阶问题的引导下，学生根据虚线的特点联想到：如果把圆平均分成8份，涂色部分占了3份，就可以表示    。又有学生说：“还可以平均分成16份，涂色部分占6份，也就是     。”第三个学生说：“还可以平均分成24份，涂色部分就是9份，也就是      。”“还有     ！”此时教师继续引导：“是啊，那可以有多少种情况啊？”学生立即回答说：“无数种！”此时学生的认知已经水到渠成，他们针对第三个问题回答说：“我发现同样的阴影部分可以用不同的分数来表示。”其实，这个问题与五年级将学习的“分数的基本性质”具有本质上的一致性。这样的问题链更能将学生的思维引向深处，学生头脑中对“分数”这一概念的理解也更加丰富和立体，通过结构化知识的构建实现对概念的深刻理解。

二、组织多形式“深”互动，从知识取向转向素养取向

“学科思想表现了学科的精神实质，它内隐于学科知识体系之内，统摄学科方法，凸显学科价值，流动于教师的教和学生学的过程之中，关照着深度教学的达成。”[3]164“我们强调‘双基’教学的重要性，但是我们更加强调以知识和技能为载体，引导学生感悟其中的数学思想。”[2]268可见，数学课堂教学存在两条线索：一条是看得到的明线，如例题、练习等；还有一条是隐藏在更深处的暗线，那就是数学思想方法。如果只教看到的，就会错失数学教学在学科素养培养上的深层价值。这条“暗线”，学生难以自己发现，需要教师有意识地引导学生将其揭示出来。从数学知识到数学思想方法的转化，需要通过互动的学习过程来实现。如何组织深层互动，实现数学思想方法的揭示？以下从两个方面分别阐述。

（一）在反思性互动中揭示数学思想方法

小学生的概括能力和元认知能力还比较欠缺，注意力往往放在知识的形成和问题解决的结果上，数学思想方法难以自然而然地形成，必须通过反思才能完成。教学中教师应有意识地组织指向思想方法的反思性互动，在学生完成知识层面的学习后，引导其对数学结论的形成过程以及数学问题的解决过程进行反思，帮助学生从关注书本知识转向关注数学思想方法，并在学生相互补充中加以整理，共同提炼形成数学思维。

例如在“长方体的认识”一课中，学生在数出长方体有6个面、12条棱、8个顶点，以及相对的面相等、相对的棱相等这几个特征后，往往就觉得已经完成了特征的学习。然而在这个单元中，更重要的教学目标是发展学生的空间观念，因此在教学中，教师在组织学生互动时提出：“大家回想一下刚才探究的过程，你们都是怎样展开联想的呢？”一生回答说：“可以从体想到面，再从面想到棱，再从棱想到顶点。”又有学生补充：“也可以反过来又面联想到体，由体也可以联想到棱……”多个学生互动后，教师用文字和图示表示出这些思维过程（如图2）。

通过对探究过程的反思性互动，空间观念的思想方法内涵得到了揭示，学习也更有深度。

（二）在对比性互动中揭示数学思想方法

同一个问题的解决，可能有多种路径，这不仅体现了算法多样化，每个路径也许蕴含着不同的数学思想方法。教师应捕捉这些契机，引发学生开展对比性互动，将关注点聚焦在不同解法的思想方法上，逐步发展学生数学学习大观念。

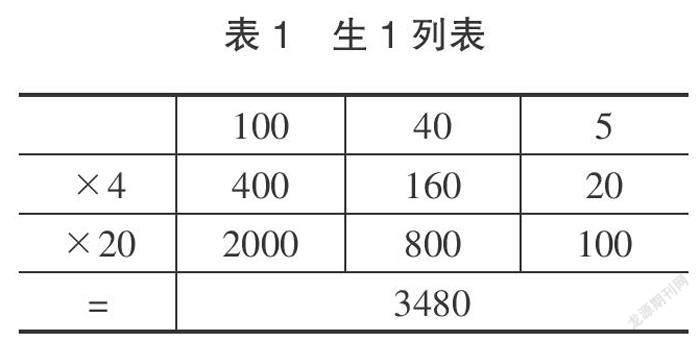
例如在学习三位数乘两位数时，生1用以下方式计算“145×24”。他将145拆分为（100+40+5），将24拆分为（20+4），然后如表1计算。

生2则呈现了另一种计算方法（如图3）：首先同样将145拆分为（100+40＋5），将24拆分为（20＋4），然后用长方形表示出它们的关系，再计算。

教师提问：“他们的思考方法有什么不同？”确定生生之间互动的焦点，学生通过对比互动发现两个学生计算结果相同，然而不同的推导过程也代表了不同的思维方法。一种是列表法，另一种是图示法。这两种方法都是数学学习中重要的方法，在学生互动中得以呈现，相互学习。

三、激发内在“深”动力，从教师立场转向学生立场

在追求以学生为中心的课堂教学改革中，“学习单”“导学案”往往成为将传统的“教”变为关注学生的“学”的代名词。然而并非使用了这些工具，学生就在进行深度学习。许多课例都让我们看到，学生依然学得非常被动。教师“牵”变成任务“牵”，学生缺乏内在的学习动力，为完成任务而完成任务，课堂明显表现出沉闷、冷漠、刻板。而深度教学是关注学生生命成长的教学，是关注学习者内在意义感的教学[3]22，教师片面地将学习任务的布置理解为学习活动的全部，显然是对学生情感态度价值观的忽视。如何激发学生深层的内在动力？

（一）情感推动，让学生求知的需要得到满足

孔子曰：“不愤不启，不悱不发。”如果学生还没进入“备战”状态，还没有摩拳擦掌跃跃欲试，即使采用任务驱动的学习方式，学生仍会处于被动状态，仍然是典型的教师立场、控制取向的教学方式。教师应关切学生的学习状态，不急于布置、介入、提醒、纠正，让学生先充分表达和思维碰撞，再通过巧妙追问，推波助澜，不斷将学生的身心带入积极的状态，让探究成为学生自己内心深处生发的动力。

（二）任务简洁，让学生主体意识得到尊重

许多教师简单地把“碎片化问题”改写成“碎片化任务”，设计繁多的填空式、碎片化、碎步子的“任务单”，仍然摆脱不了以教师为中心的“灌输”，限制了学生主体意识的发挥。只有真正站在学生立场，尊重他们探究的主体意识，设计具有启发性、简洁的大任务、大问题，才能真正实现教学中主体的转变，让学生更深地体会到学习所带来的意义和价值。

例如，在“长方体的认识”一课中，我们通过冬奥会的“冰立方”引发学生对长方体特征的探究欲望，并设计了以下的两个大任务和四个大问题。任务一：认识面、棱、顶点的概念。本任务设计了两个问题：1.哪个面和哪个面相交成哪条棱？2.哪条棱和哪条棱相交成哪个顶点？任务二：探究长方体的特征。本任务要求学生围绕“面”“棱”“顶点”探究它们的数量以及形状特征，并提出两个问题：1.在数面、棱、顶点时，你有什么好方法做到不重复不遗漏？2.你发现的每个结论的依据是什么？

这里的两大任务和四大问题取代了琐碎的浅层问题，学生主动观察、记录、对比、发现，在自主合作学习中不但总结出长方体的特征，更运用已学知识进行推理，想办法证明他们的结论，寻求优化的方法。学生思维的完整性得到了尊重，学生在探究中体会到数学的魅力。

综上所述，小学数学深度课堂，应遵循深度教学的理念和小学数学学与教的心理规律，着眼于数学本质、思想方法和情感态度价值观，点燃学生求知热情，组织学生开展有价值的“真探究”，从而获得数学学科核心素养的发展，真正改变低效课堂，实现减负增质。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2022版）[M].北京：北京师范大学出版社，2022：8.

[2]何小亚.数学学与教的心理学[M].广州：华南理工大学出版社，2021.

[3]郭元祥.深度教学[M].福州：福建教育出版，2021.

责任编辑：贾凌燕

*本文系广州市教育科研基地项目“小学数学协作建模学习的设计与实施研究”（14XZ03）研究成果之一。

收稿日期：2022-10-22

作者简介：孙颖，广州市天河区体育东路小学副校长，高级教师，广东省特级教师，广州市名师工作室主持人，主要研究方向为小学数学教学。