一道教材例题的“变身”

文／尹雪蔓

数学解题不应只局限于一道题目的本身，而应能比较类似的题目，用变化的眼光去发现它们之间的联系，在比较中深化对知识的理解，掌握解题方法，提高举一反三和灵活应变的能力。

原题呈现（苏科版数学教材八年级下册第69 页例3）已知：如图1，在▱ABCD中，点E、F在AC上，且AE=CF。求证：四边形EBFD是平行四边形。

图1

【分析】我们可以利用“平行四边形的性质→寻找三角形全等→线段和角相等→判定平行四边形”的思路解决问题。

证法一：根据平行四边形对边相等的性质定理可知AB=CD，根据平行四边形的定义可知AB//CD，所以∠BAE=∠DCF。又因为AE=CF，所以△ABE≌△CDF（SAS），所以BE=DF，∠BEA=∠DFC。根据“等角的补角相等”可得∠BEF=∠DFE，所以四边形EBFD是平行四边形。

证法二：同“证法一”可证得BE=DF。同理，通过证明△ADE≌△CBF（SAS）得到DE=BF，所以四边形EBFD是平行四边形。

教材中给予的解法是利用“对角线互相平分”的判定定理来证明。其实质是想告诉我们，解决本题，除了“寻找”全等三角形，还可以“构造”全等三角形。如图2，连接BD，BD交AC于点O，构造出三角形（△BEO、△BFO、△DEO、△DFO），并证明所构造的三角形全等（△BEO≌△DFO、△BFO≌△DEO），进而通过线段和角相等来证明平行四边形。

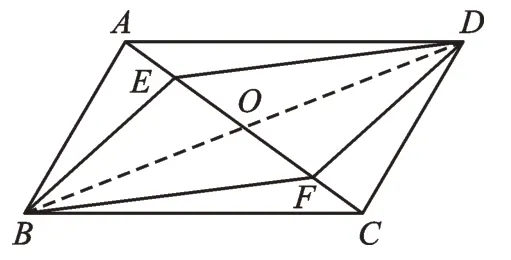
图2

变式1已知：如图3，在▱ABCD中，BE⊥AC，DF⊥AC，垂足分别为E、F。求证：四边形EBFD是平行四边形。

图3

【解析】变式1 是将原例题中的“AE=CF”变成了“BE⊥AC，DF⊥AC，垂足分别为E、F”。此时，我们只需连接BD，直接证明△BOE≌△DOF，得出对应线段和角的相等关系，从而证明平行四边形。

变式2已知：如图4，在▱ABCD中，∠ABC、∠ADC的平分线分别交对角线AC于点E、F。求证：四边形EBFD是平行四边形。

图4

【解析】变式2 是将原例题中的“AE=CF”变成了“∠ABC、∠ADC的平分线分别交对角线AC于点E、F”，同变式1 一样，只是条件改变，证明方法类似（连接BD）。

变式3如图5，▱ABCD的对角线AC与BD相交于点O，点E、F分别在OB和OD上。

图5

（1）当BE、DF满足什么条件时，四边形AECF是平行四边形？请说明理由；

（2）当∠AEB与∠CFD满足什么条件时，四边形AECF是平行四边形？请说明理由。

【解析】此题由原例题的条件“AE=CF”变成了第（1）问的答案“BE=DF”，第（2）问也可以通过上述几个变式的经验得到结论（相等）。通过上述几道变式，我们可以发现，点E、F的位置是解题的关键，其变化的本质特征是点E、F关于对角线交点O对称。

同学们要重视教材上的例题和习题，学会从“变”的现象中发现“不变”的本质，从“不变”的本质中探究“变”的规律。

拓展1已知：如图6，点E、F分别是▱ABCD对角线AC所在直线上的两点，且AE=CF。求证：四边形EBFD是平行四边形。

图6

【解析】本题是图1 的拓展，点E、F的位置从“对角线上”变化为“对角线所在的直线线上”。证明方法类似，在此不再赘述。

拓展2如图7，▱ABCD的对角线AC与BD相交于点O，AC=15cm。点E、F分别是线段OA、OC上的动点，点E从点A出发，以2cm/s 的速度向点O运动；点F从点O出发，以3cm/s的速度向点C运动；当一点到达终点时，停止运动。若点E、F同时开始运动，设运动时间为ts，当t为何值时，四边形EBFD是平行四边形？

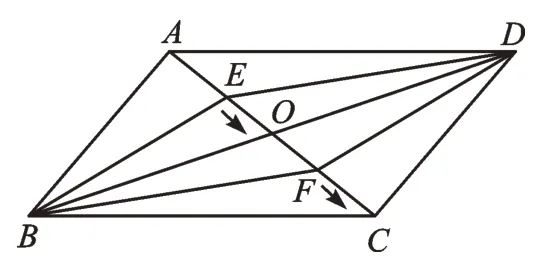
图7

【解析】本题是把定点问题变成了动点问题。此时，我们可以根据已探究出的问题本质“只要确保点E、F关于对角线交点O对称”，即可判定平行四边形。