聚焦要领，明辨易混点

2023-05-25 01:09文／李青

文／李青

在中考中，我们会遇到考查特殊四边形的概念和相关定理的问题，理解和掌握这些知识点是解决问题的关键。如果掌握不牢，记忆混淆，解题时就会得到错误的过程和结论。下面，我们举例分析四边形中的易混淆点，希望对同学们的学习有所帮助。

一、混淆图形条件

例1如图1，在▱ABCD中，对角线AC、BD相交于点O，且△AOB是边长为4的等边三角形，求▱ABCD的面积。

图1

【解析】∵△AOB是等边三角形，

∴AB=OA=OB=4。

又∵四边形ABCD是平行四边形，

∴AC=BD=8。

∴平行四边形ABCD是矩形。

∴∠ABC=90°。

在Rt△ABC中，∵AB=4，AC=8，

【点评】一些题目由于图形的误导，同学们可能会做出错误的判断。本题的图形就可能会让大家把平行四边形ABCD默认为是矩形，而不加以证明。因此，解决本题的关键是先证明平行四边形ABCD是矩形。

例2如图2，四边形ABCD的对角线AC和BD相交于点O，有以下条件：①AB=AD；②∠DAB=90°；③AO=CO，BO=DO；④四边形ABCD是矩形；⑤四边形ABCD是菱形；⑥四边形ABCD是正方形，则下列推理不成立的是（）。

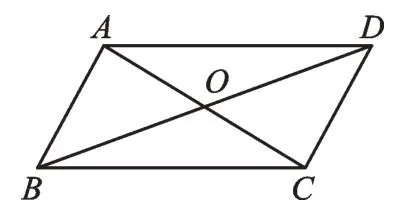
图2

A.①④⇒⑥ B.①③⇒⑤

C.①②⇒⑥ D.②③⇒④

【解析】有一组邻边相等的矩形是正方形，所以A选项是正确的；对角线互相平分且有一组邻边相等的四边形是菱形，所以B 选项是正确的；对角线互相平分且有一个角是直角的四边形是矩形，所以D 选项是正确的；C选项的推理不成立。

【点评】牢记特殊四边形的性质和判定是解决此类问题的关键。矩形、菱形、正方形都是特殊的平行四边形，同学们在判断时，一定要先判断它是否是平行四边形。

例3如图3，点E、F、G、H分别是四边形ABCD各边的中点，且AC=BD，试判断四边形EFGH的形状________。

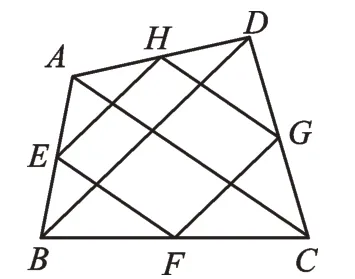
图3

【解析】∵点E、F、G、H分别是四边形ABCD各边的中点，

根据三角形中位线的性质，

可得EF∥AC，GH∥AC，

EF=，GH=，EH=

∴FE∥GH，且EF=GH。

∴四边形EFGH是平行四边形。

又∵AC=BD，∴EF=EH，

∴四边形EFGH是菱形。

【点评】许多同学容易混淆中点四边形的形状。其实，判别方法并不难，我们可以总结规律如下：顺次连接任意四边形ABCD各边中点一定得平行四边形，且当四边形ABCD的对角线相等或互相垂直时，它的中点四边形邻边也相等或互相垂直，则可以确定中点四边形的形状。

例4在下列图形：矩形、菱形、正方形、平行四边形中，是中心对称图形，但不一定是轴对称图形的是________。

【解析】平行四边形是中心对称图形，但不一定是轴对称图形。

【点评】解决此题的关键是分清中心对称图形和轴对称图形的概念。平行四边形是中心对称图形，但不一定是轴对称图形，同学们动手操作一下就会知道。而矩形、菱形、正方形这些特殊的平行四边形，既是轴对称图形，也是中心对称图形。