蜂窝钢管混凝土抗侵彻性能实验研究*

赵宏远，武海军，董 恒，吕映庆，黄风雷

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

随着高速侵彻动力学的发展，武器弹药的毁伤威力和打击精度逐渐提高，国防工程面临的威胁日益严峻[1]。采用高强度材料披覆在工事表面，可以有效降低弹体对工事的毁伤程度。高强度材料（如纤维混凝土[2-3]、超高性能混凝土[4]和钢管混凝土[5]等）可以利用自身强度，降低弹体侵彻深度，以达到防护的目的。钢管混凝土（concrete-filled steel tube,CFST）是由钢管和混凝土组成的一种新的结构，钢管和混凝土的综合作用使二者的延性和强度大大增加，混凝土的破坏形式由脆性破坏变为延性破坏，有效提高了结构的抗侵彻性能[6]。相比于其他高强度材料，钢管混凝土造价低、强度高、施工方便，非常适合作为遮弹层。蜂窝钢管混凝土是由多个单孔六边形钢管混凝土按照一定规律排布组合而成的防护结构，如图1 所示。与其他结构的钢管混凝土相比，蜂窝钢管混凝土排布紧密、施工方便，更适合工程化应用。

图1 蜂窝钢管混凝土[5]Fig. 1 CFST with honeycomb structure[5]

目前，关于钢管混凝土抗侵彻性能的研究较少。甄明等[7-8]采用12.7 mm 穿甲弹进行了单孔圆形钢管混凝土侵彻实验，重点研究了钢管混凝土的侵彻模式、侵彻深度、漏斗坑尺寸和抗侵彻性能，表明钢管混凝土具有良好的抗单发和多发的打击能力。蒙朝美等[9]采用12.7 mm 穿甲弹进行了单孔多边形钢管混凝土靶侵彻实验，设置了圆形钢管、四边形钢管、六边形钢管3 个对照组，给出了3 种钢管的典型破坏形式。这些实验的对象均为单孔钢管混凝土，没有考虑多个钢管的协同作用，具有一定的局限性。詹昊雯[10]采用12.7 mm 枪弹进行了蜂窝钢管混凝土侵彻实验，研究了单孔六边形和蜂窝钢管混凝土的抗侵彻能力差异。王起帆等[11]研究了钢管混凝土组合结构，采用15 mm 弹体对蜂窝钢管混凝土和钢筋混凝土进行了侵彻实验，表明蜂窝钢管混凝土的侵深和开坑面积均小于钢筋混凝土的。

为了清晰地描述弹体侵彻钢管混凝土的各种工况，定义弹靶尺寸比U为单个钢管截面外接圆直径与弹体直径的比。上述研究中，弹体均为12～15 mm 枪弹，约束钢管外接圆直径多大于150 mm，则U＞10。弹体侵彻过程中，弹体仅同混凝土接触，钢管主要为增强混凝土围压，并不直接参与整个抗侵彻过程。但在防护工程中，弹体直径与约束钢管外接圆直径可能相近，工况多为0.8＜U＜6.0。则着靶点不同时，弹体与钢管壁的接触程度及靶板破坏形式也不同，靶板的抗侵彻能力有区别。现有的研究结果无法为相关防护工程的建造提供参考，因此，有必要开展0.8＜U＜6.0 时蜂窝混凝土靶板抗侵彻性能研究。

本文中，开展0.8＜U＜6.0 时蜂窝钢管混凝土侵彻实验，获得不同着靶点和不同壁厚时靶板的破坏形式；开展六边形钢管混凝土准静态压缩实验，定量分析钢管的强度增强效应，同时对原有的混凝土侵深经验公式进行修正，获得适用于蜂窝钢管混凝土的最大侵深计算公式。研究结果拟为相关工程设计提供参考。

1 实 验

1.1 弹体

截卵型弹体长为647 mm，直径为100 mm，弹体头部曲率半径与弹体直径的比φ=3，如图2 所示。弹体材料为30CrMnSi2A，密度为7 850 kg/m3，弹性模量为210 GPa，屈服强度为1 413 MPa，经过热处理的弹体洛氏硬度不低于48。弹体内部装填模拟物，密度约1 650 kg/m3，弹体总质量为20.57～22.42 kg。

图2 弹体照片Fig. 2 A photo of the projectile

1.2 靶体

设置3 种结构靶板，壁厚5 mm 蜂窝钢管混凝土靶3 块，壁厚8 mm 蜂窝钢管混凝土靶3 块，作为对照组的无钢管混凝土靶1 块。将组成蜂窝钢管混凝土靶的单个六边形钢管混凝土作为一个单元，单元边长为80 mm，壁厚分别为5 和8 mm，材料为Q345 钢。靶体所用混凝土材料均为含钢纤维的C100 自密实混凝土，测得密度为2 420 kg/m3，自然养护条件（28 d）下混凝土标准立方体抗压强度为101 MPa。着靶点有中心点和交点（见图3），通过移动靶板位置，实现不同着靶点的侵彻实验。

图3 靶体的结构和照片Fig. 3 The structure and photo of the target

为了模拟半无限靶并控制钢材用量，选择蜂窝钢管混凝土的靶板前部为厚400 mm 蜂窝靶板，后部为厚400 mm 的C100 自密实混凝土背板，并一体浇筑成型。靶板直径为1 600 mm，总厚度为800 mm。为了增加围压，靶板外部使用Q235 钢板进行围箍。蜂窝钢管混凝土靶如图3 所示。无钢管混凝土靶不含蜂窝，总厚度也为800 mm。

2 结果和分析

2.1 结果

由125 mm 口径滑膛炮发射弹体，改变装药量、控制弹体发射速度，采用高速摄影系统记录弹体的着靶姿态和着靶速度。弹体的着速为271～352 m/s，实验后的弹体保持完整的整体结构，无明显变形，如图4 所示。靶体表面的破坏情况如图5 所示，具体结果见表1。

图4 实验后的弹体Fig. 4 The projectile after experiment

图5 靶体的破坏形态Fig. 5 Damage of targets

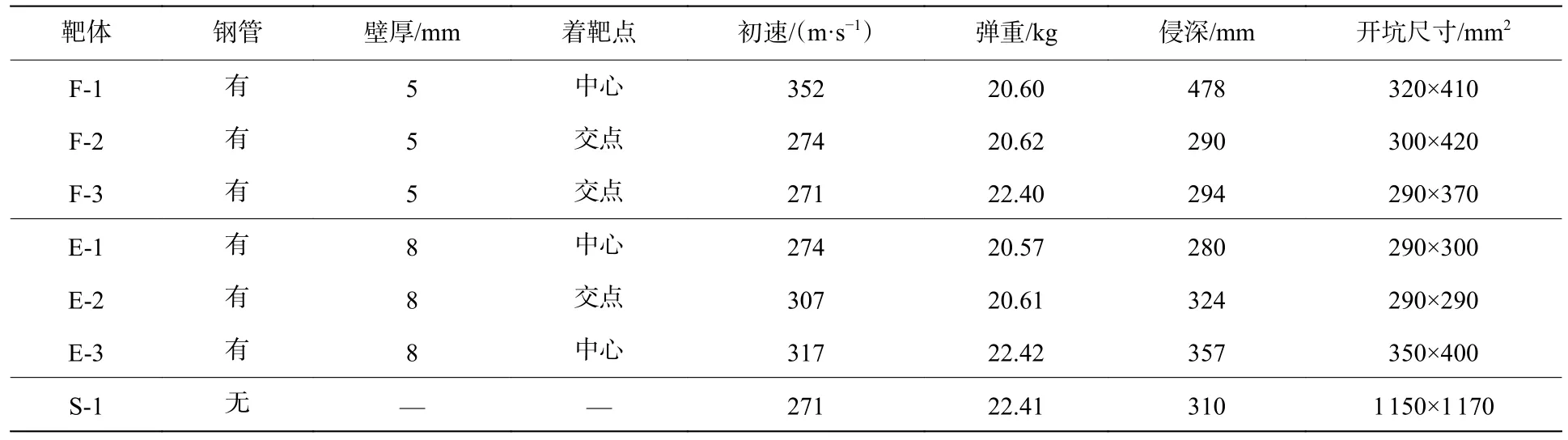
表1 侵彻实验结果Table 1 Results of the penetration experiments

由图5(a)可见，对于蜂窝钢管混凝土靶，当中心着靶时，弹体直接命中的单元会发生严重破坏，单元内的混凝土已经完全脱出，临近单元内混凝土出现不同程度剥落，但剥落程度相对较小。由图5(b)～(e)和图6 可见，当交点着靶时，由于钢和混凝土材料强度的不均匀性，弹体受到偏转力和力矩的影响，在侵入靶体30～100 mm 时发生偏转，并最终侵入着靶点的临近单元中。交点着靶时，侵彻前期钢管发生明显变形，钢管的挤压作用使着靶点附近单元内混凝土均出现剥落。相比传统混凝土的破坏（见图5(g)），钢管壁限制了靶体表面开坑的面积和深度。

图6 交点着靶时弹体偏转痕迹和钢管剪切破坏Fig. 6 Deflection marks of projectile and shear failures of steel tube wall under intersecting point impact

蜂窝钢管混凝土靶和无钢管混凝土靶的表面裂纹扩展，如图7 所示。钢管壁增强了混凝土的韧性并影响了应力波的传递，蜂窝钢管混凝土靶的表面均为短裂纹且无主裂纹，裂纹延伸范围均小于两个单元。无钢管混凝土靶表面的主裂纹均为大裂纹，裂纹一直延伸到靶板边界，裂纹中可见明显的断裂钢纤维。

图7 有无钢管混凝土靶的表面裂纹Fig. 7 Surface cracks of targets with or without steel tube

2.2 侵彻深度

相近的实验有一定的速度差异，为了控制干扰变量，需要消除速度的影响。而侵彻深度与初速成正比，可按比例换算弹体在不同着靶速度下的侵彻深度。为比较相同壁厚、不同着靶点对侵深的影响，将实验 F-1 的速度换算至274 m/s 与实验F-2 对比，将实验E-1 的速度换算至307 m/s 与实验E-2 对比，换算后的结果见表2。图8 为侵彻深度对比。

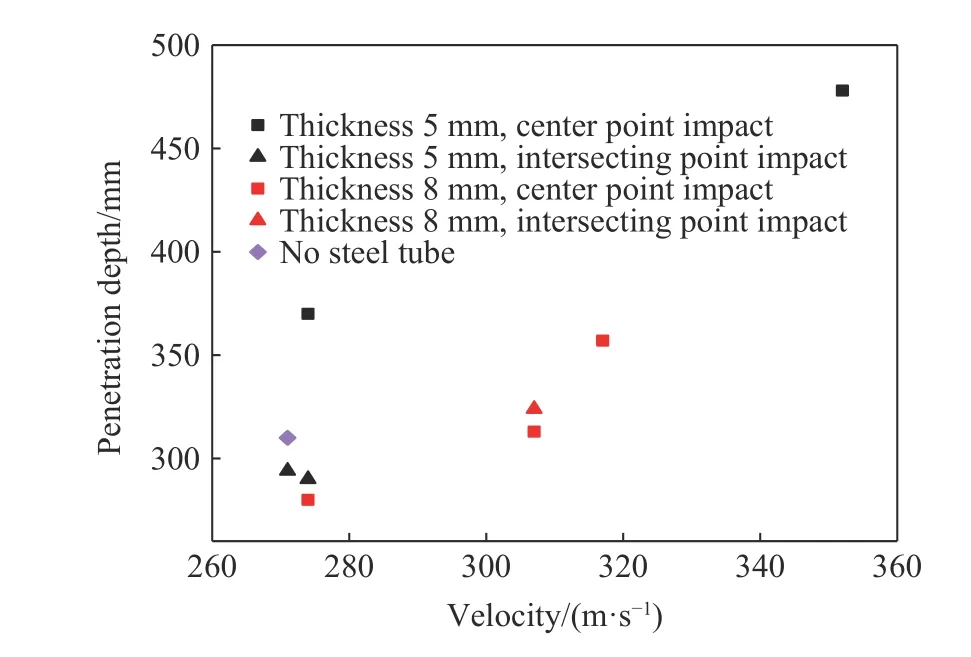
图8 实验及按初速换算后的侵彻深度Fig. 8 Experimental and converted penetration depths based on initial velocity

表2 按初速换算后的侵彻深度Table 2 Penetration depths converted by initial velocity

2.2.1 着靶点的影响

由图8 可见，当壁厚为5 mm、速度为274 m/s 时，中心着靶的侵深远大于交点着靶的，二者相差约25.8%；当壁厚为8 mm、速度为307 m/s 时，中心着靶的侵深与交点着靶的差别较小，即着靶点位置对侵深的影响程度具有离散性。这可能是因为，当着靶点为钢管交点时，在着靶瞬间弹体与钢管壁发生碰撞，压缩作用使钢管壁产生剪切破坏，同时使弹体发生偏转。侵深达到约100 mm 时，弹体侵入临近蜂窝单元，不再与钢管壁接触。整个侵彻过程中，钢管壁直接阻碍弹体运动的前半段较短，主要起致偏作用。弹体侵入临近单元后，因角度偏转，弹体受力更复杂，且弹体头部可能与钢管壁发生二次碰撞，所以着靶点位置对侵深影响具有离散性。由图6 明显可见，弹体偏转痕迹和钢管壁的剪切破坏。

2.2.2 钢管壁厚的影响

由图8 可见，当着靶点为中心点、速度为274 m/s 时，壁厚5 mm 靶板的侵深比8 mm 的增加了约32%，即壁厚对侵深影响较大。这是由于，钢管为核心混凝土提供了围压，增强了核心混凝土的强度，同时阻止了核心混凝土裂隙的发展，增加了其延性。钢管壁厚越大，钢管产生的约束效应越明显，越能增强核心混凝土的强度，使侵深下降。

在无钢管混凝土靶侵彻实验中，侵彻深度仅为343 mm。这是因为，弹体侵入靶板后，向右上方发生严重倾斜，且弹体侵入靶板一定距离后，向右上方弹出，造成侵深过小。

2.3 不同弹靶尺寸比时靶体的破坏

王起帆等[11]进行了15 mm 枪弹侵彻钢管外接圆直径240 mm 蜂窝混凝土的实验，该实验中U=16；而本文实验中U=1.6。靶板的破坏形式分别如图9～10 所示，可见弹靶尺寸比显著影响靶板表面的破坏形式。

图9 当U=16 时靶板破坏[11]Fig. 9 Failure of targets when U=16[11]

图10 当U=1.6 时靶板破坏Fig. 10 Failure of targets when U=1.6

当U=16 时，靶板中钢管部分不直接参与侵彻，侵彻结束后，钢管仍为六边形，无明显损伤及变形。混凝土只发生小部分崩落，崩落范围仅局限在着靶点单元，临近单元无裂纹。这是因为，弹靶尺寸差距过大，致使应力波传递到钢管并发生透射后，已严重衰减，未达到混凝土的破坏条件。

当U=1.6、着靶点不同时，钢管参与侵彻的程度也不同。中心着靶时，着靶点单元钢管保持完整，但角部发生钝化，六边形钢管截面形状趋于圆形。着靶点单元混凝土破坏严重，靠外侧的混凝土已经完全脱出。着靶点临近位置单元混凝土出现轻微剥落。交点着靶时，着靶点钢管发生剪切破坏，部分钢管被撕裂脱落，其余钢管向内挤压变形。着靶点临近位置单元混凝土破坏都较严重。两种着靶方式下，着靶点附近单元均出现了细微裂纹，但裂纹长度较短。

3 钢管的增强效应

侵彻过程中，钢管提供的侵彻阻力包括两种，一种为直接侵彻阻力，一种为间接侵彻阻力。其中，直接侵彻阻力是弹体与钢管直接接触产生的侵彻阻力；间接侵彻阻力是以钢管为核心混凝土提供了围压，增强了其强度及延性，从而间接增加的阻力。本文中，对蜂窝钢管混凝土的单个单元即单孔六边形钢管混凝土，开展单轴压缩实验，获得不同壁厚时单孔六边形钢管混凝土的应力-应变曲线及破坏形式，由实验数据分析钢管的整体增强效应。

3.1 单轴压缩实验

使用微机控制电液伺服压剪试验机YAW7506，对不同壁厚的单孔六边形钢管混凝土进行了单轴压缩实验。实验试件共3 种：边长80 mm 的六边形C100 自密实混凝土土柱；壁厚5 mm 单孔六边形钢管混凝土；壁厚8 mm 单孔六边形钢管混凝土。试件所用的混凝土和钢材料与第2 节一致。试件高度均为300 mm，试件结构如图11 所示。

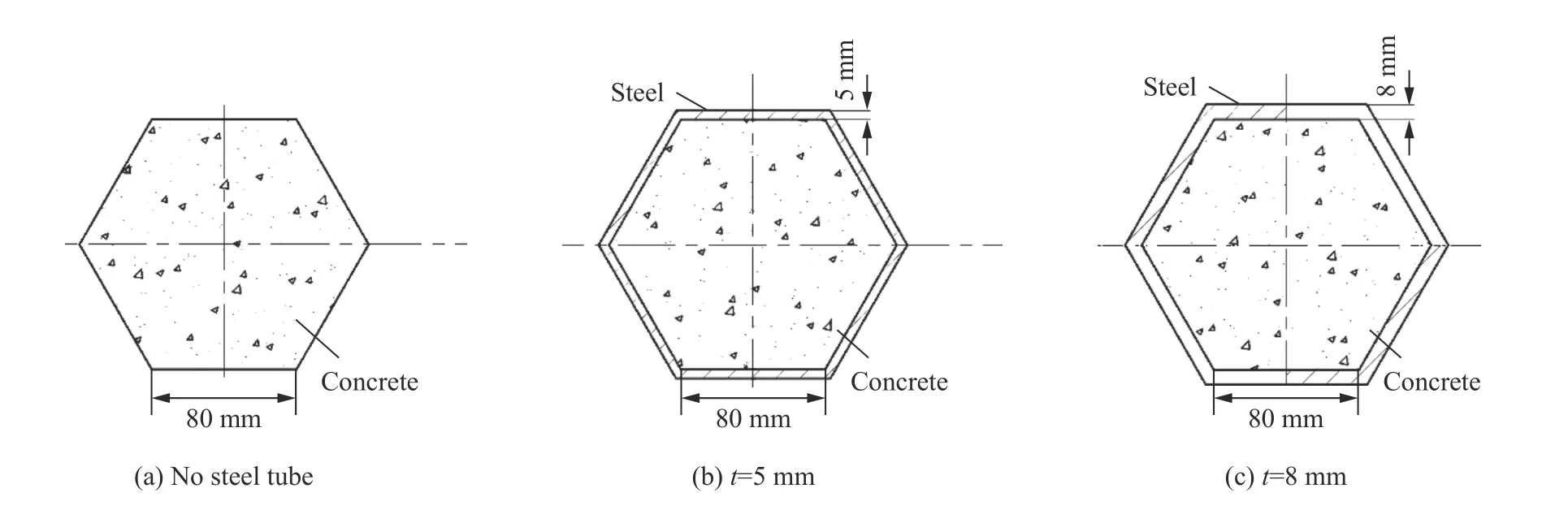
图11 实验试件的结构Fig. 11 Structures of experiment specimens

实验结果见表3，试件的承载力-应变曲线如图12 所示，典型破坏形式如图13 所示。

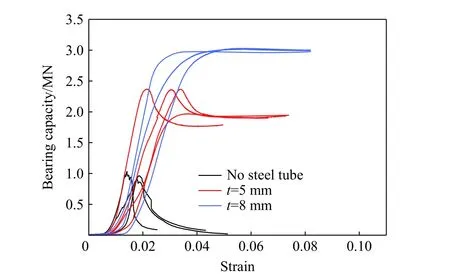
图12 试件的承载力曲线Fig. 12 Bearing capacity curves of specimens

图13 试件的破坏形态Fig. 13 Damage of specimens

表3 核心混凝土的强度增强因数Table 3 Strength enhancement coefficients of core concretes

3 种试件的破坏形式及其承载力曲线有明显不同。对无钢管混凝土，当压力达到约75%极限承载力时，试件侧面混凝土大量剥落，但未出现贯穿裂纹。当压力达到试件最大承载力时，出现轻微爆裂声。试件发生脆性破坏，承载能力迅速下降，出现了两条纵向长裂纹，从顶部贯穿到底部。由于钢纤维增加了试件的延性，试件承载力曲线的下降段斜率小于岩石和素混凝土等传统脆性材料。而壁厚5 和

8 mm 的钢管混凝土，在达到极限承载力前试件均无明显变形。达到极限承载力后，试件并未发出爆裂声，可见钢管内部混凝土延性增强了。在混凝土压碎变形产生的侧向压力作用下，钢管逐渐鼓曲，钢管对混凝土的约束作用随着钢管侧向变形的增加而增大。当钢管受力达到强化阶段时，试件变形和承载能力趋于稳定，试件整体呈上、中和下三段鼓曲破坏。由承载力曲线，壁厚5 mm 试件达到最大承载力后，曲线出现缓慢下降段，下降速度远小于无钢管试件的，而壁厚8 mm 试件出现了平台段。

3.2 增强效应

钢管为核心混凝土提供了围压，使核心混凝土处于三维受压状态，其抗压强度出现了明显增强。定义强度增强因数k为被钢管增强后的核心混凝土抗压强度与无钢管混凝土抗压强度的比。强度增强因数k越大，钢管提供的增强效应越强。由文献[12-15]，相同材料、不同尺寸和形状的混凝土的强度差异很大。为了更清晰地分析钢管对核心混凝土强度的增强效应，记fc为混凝土标准立方体的无侧限抗压强度，记fc2为本文实验中的六边形C100 自密实混凝土土柱的强度（即试件1～3 的抗压强度平均值）。

确定强度增强因数关键在于，确定不同壁厚钢管的围压 σr。计算不同壁厚钢管提供的围压时，需做两个假设。(1) 钢管服从von-Mises 屈服准则。(2) 三维受压下的六边形截面混凝土的强度极限条件与圆形截面混凝土的相同，六边形混凝土强度fc*与围压 σr之间具有线性关系[16]：

式中：fc为混凝土标准立方体的无侧限抗压强度。

为了消除几何特征的影响，在本实验的基础上确定核心混凝土强度增强因数k时，无钢管时混凝土抗压强度应该使用六边形C100 自密实混凝土柱的实测强度fc2，而不应使用混凝土标准立方体无侧限抗压强度fc。式(1)则变为：

式中：fc2为六边形C100 自密实混凝土柱的实测强度。

此处，使用fc2只是为了在求k时消除几何特征产生的影响。在计算围箍因数和侵深时，混凝土抗压强度仍使用标准立方体的无侧限抗压强度fc。

计算简图如图14 所示，钢管壁壁面压力σ3与混凝土所受围压 σr互为反作用力，二者数值相等。钢管的壁厚为t，外边长为B，内边长为b。仅研究B/t≥10 的薄壁钢管混凝土，因钢管壁较薄，可认为钢管壁环向拉应力 σ2均匀分布，且σ3≪σ2，则von Mises 屈服准则退化为：

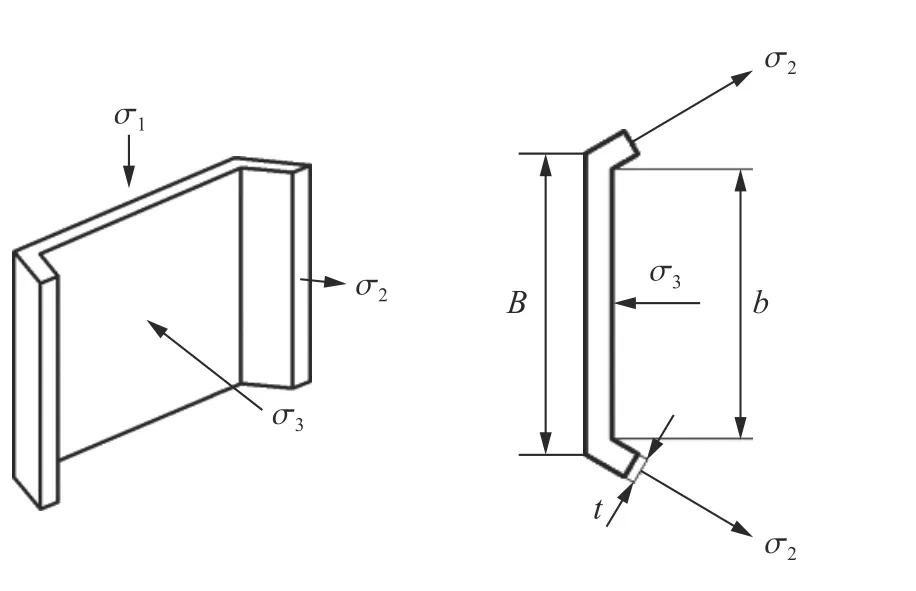
图14 钢管壁的受力分析Fig. 14 Stress analysis f steel tube wall

可解得：

由钢管壁的平衡条件可得，钢管环向拉应力 σ2与钢管围压 σ3的关系为：

联立式(1)～(3)解得，钢管混凝土承载力N为：

式中：As为钢管横截面积，fs为钢管屈服强度，Ac为混凝土横截面积。

如已知钢管混凝土承载力，根据式(6)，可以求得单轴压缩实验中试件破坏时混凝土所受围压 σr，代入式(2)即可求得该围压下的核心混凝土强度和强度增强因数。核心混凝土强度增强因数的计算结果见表3。

围箍因数是衡量钢管混凝土围箍效应最常用的参数。实验结果显示，核心混凝土强度增强因数与围箍因数呈线性关系：

式中：围箍因数 δ =Asfs/(Acfc) 。线性关系如图15 所示，拟合效果较好（R2=0.903）。

图15 核心混凝土强度增强因数与围箍因数的关系Fig. 15 The relationship between the strength enhancement factor of core concrete and the hoop factor

3.3 最大侵深公式

由以上可知，中心着靶时，钢管不直接参与侵彻，只提供间接侵彻阻力，一般情况下，此时的侵深最大。在工程中，以最大侵彻深度作为防护结构的设计参考依据更具安全性。因此，有必要给出蜂窝钢管混凝土的最大侵彻深度计算公式，即中心着靶时弹体的侵彻深度计算公式。

以上拟合了核心混凝土强度增强因数与钢管混凝土围箍因数的关系，给出了不同壁厚钢管对核心混凝土强度增强效应即钢管提供的间接阻力的定量分析。用增强后的核心混凝土强度kfc替换侵深经验公式中的混凝土标准立方体无侧限抗压强度fc，即可得到适用蜂窝钢管混凝土的最大侵深计算公式。

金栋梁等[17]和何翔等[18]分析了20 余种常用的侵彻经验公式及其特点和适用范围，在量纲分析基础上，给出了合理的经验公式：

式中：x为侵彻深度；d为弹体直径；K2为质量修正因子；对截卵型头部弹体，N1=0.18(lh/d)0.5+0.56 ，lh为弹体长度；r为钢筋配比相关因数，这里r=0；m为弹体质量； ρc为靶体密度；fc为混凝土标准立方体无侧限抗压强度；重力加速度g=10 m/s2；v0为侵彻速度。质量修正因子为：

在此基础上修正，用kfc替换fc，则式(8)变为：

使用修正的经验公式，对侵彻结果进行计算，见表4。

表4 实验和计算的侵彻深度Table 4 Experimental and computational penetration depths

由表4，实验E-1 和E-3 结果预测较好，F-1 预测结果略有误差。这是因为，实验靶体前400 mm 为蜂窝结构，后400 mm 为自密实混凝土结构，当侵深超过400 mm 时，蜂窝无法继续起作用，致使实际侵深大于预估侵深。因此，改进的经验公式可以合理地预测侵深。

4 结 论

开展了弹体在速度270～352 m/s 下侵彻无钢管混凝土和蜂窝钢管混凝土靶的实验，对不同钢管壁厚的单孔六边形钢管混凝土靶进行了单轴压缩实验，探讨了蜂窝钢管混凝土的抗侵彻性能及机理。得到了以下结论。

(1) 当0.8＜U＜6.0 即弹体直径同钢管边长相近时，着靶方式对靶体表面破坏形式的影响明显。中心着靶时，着靶点单元钢管部分保持完整，但角部发生钝化，钢管截面形状由六边形趋向于圆形。着靶点处单元混凝土破坏严重，临近位置单元内混凝土出现轻微剥落。交点着靶时，着靶点处钢管发生剪切破坏，部分钢管被撕裂脱落，其余钢管向内挤压变形。着靶点临近位置单元混凝土破坏都较严重。

(2) 蜂窝钢管混凝土的钢管壁厚和侵深关系较密切，壁厚5 mm 蜂窝钢管混凝土的侵深比8 mm 壁厚的增加了约32%；着靶方式对侵深的影响具随机性。

(3) 蜂窝钢管混凝土抗侵彻过程中，钢管增强了核心混凝土的强度和延性。且钢管对核心混凝土的强度增强因数与钢管混凝土的围箍因数之间呈线性关系。

(4) 改进的侵深经验公式可以用于预测弹体侵彻蜂窝钢管混凝土的最大侵深。