超高性能混凝土HJC 本构模型参数确定及应用*

宋 帅，杜 闯,2，李艳艳

（1. 河北工业大学土木与交通学院，天津 300401；2. 河南省特种防护材料重点实验室，河南 洛阳 471023）

超高性能混凝土（ultra-high performance concrete, UHPC）是近年来发展起来的一种新型水泥基材料，具有较高的强度、韧性、抗冲击性以及耐久性[1-3]。杜忠等[4]对高延性混凝土的抗爆性能开展了研究，发现在爆炸冲击作用下，混凝土的强度和韧性越高，对冲击波冲量的吸收能力越强。若将UHPC 应用于防护工程，必将显著提高防护结构的抗力水平。目前，我国对于UHPC 材料的研究和应用尚处于起步阶段，其抗爆性能的研究成果并不丰富，这严重阻碍了UHPC 在国防工程中的应用。开展UHPC 抗爆性能研究，通常有试验、理论分析和数值模拟3 种方法。由于试验费用较高，存在一定的危险性和环境影响[5]，并且UHPC 爆炸试验处于高应变率状态下，持续时间极短，普通的传感器或应变片很难精确记录基体在抗爆破坏过程中的变化情况。而理论分析简化过多，难以得到可靠的方程解。因此，数值模拟成为开展UHPC 抗爆性能研究的重要方法。

然而，大量实践表明：数值模拟结果的准确性取决于动态本构模型的选择及参数的确定。因此，开展UHPC 动态本构模型的研究非常必要，这对于了解UHPC 结构抗爆破坏机理，建立UHPC 结构的抗爆性能设计方法，推广其在国防工程中的应用都具有重要意义。目前，在爆炸数值模拟中常用的混凝土动态本构模型有Riedel-Hiermaier-Thoma (RHT)本构模型[6]、K&C 本构模型[7]和Holmquist-Johnson-Cook(HJC)本构模型[8]。其中RHT 本构模型对混凝土损伤裂纹的描述较成功，但其参数较多，标定过程复杂，并且UHPC 相关试验数据较少，很难采用岩石材料参数的确定方法去标定UHPC 材料参数。K&C 本构模型可以自动生成大量参数，为研究人员提供了极大的便利。但模拟试验表明，针对强度较高的混凝土，自动生成的参数往往达不到精度要求，而关于K&C 参数标定的相关研究内容较少。在损伤表达方面，K&C 本构模型考虑较全面，但模拟效果表明，其损伤程度也往往偏大[9]。HJC 本构模型能够很好地描述材料在强动载作用下的力学行为，且该模型参数数量相对较少、物理意义明确，其中大多数参数可以由试验及公式获得[10]，使该本构模型在高压、大应变、高应变率工况的数值模拟计算中，实现了简单性和准确性的良好折中。因此，HJC 本构模型在混凝土爆炸数值模拟中被广泛使用[11]。如Liu 等[12]利用HJC 模型对钢筋混凝土材料进行了爆炸数值模拟，分析了混凝土的动态力学响应规律。张志刚等[13]在数值模拟中，采用HJC 模型建立了混凝土板构件，研究了碳纤维布加固混凝土板的抗爆能力。张志华等[14]利用HJC 模型建立了不同强度的混凝土块，分析了爆炸工况下混凝土内部的应力波传递规律。然而，在HJC 本构模型的参数确定方面，由于缺少相关试验，大多数研究人员套用已有文献相似材料的计算参数，导致计算结果与试验结果差距较大。近年来，针对该本构模型参数的确定，国内外学者开展了大量研究，并取得了一定成果。如任根茂等[15]基于普通混凝土相关力学试验，确定了适用于不同强度的普通混凝土HJC 模型参数，并通过模拟侵彻试验进行了验证。陈睿等[16]基于霍普金森压杆（split Hopkinson pressure bar, SHPB）试验，提出了一种混凝土材料动态模型参数的分阶段反求法。张社荣等[17]基于动、静态力学试验对HJC 原始参数进行了修正，并通过模拟SHPB 试验验证了参数的有效性。熊益波等[18]利用三轴围压数据，在不考虑损伤和应变率的基础上给出了一套确定混凝土强度参数的方法。李鹏[19]通过对强度参数进行敏感性分析并结合试验调整参数，确定出了适用于爆炸荷载的混凝土HJC 本构模型参数。但以上研究大多是对普通混凝土HJC 本构模型参数进行研究确定，针对超高性能混凝土HJC 本构模型参数的研究未见报道。

本文中，以HJC 本构模型为基础，通过相关力学试验和现有文献结论确定一组适用于UHPC 的动态本构模型参数。以UHPC 构件抗爆试验数据为依据，验证参数的有效性。在此基础上，开展UHPC 单向板抗爆性能研究，分析配筋和尺寸效应对UHPC 单向板爆炸结果的影响。

1 参数确定

1.1 HJC 模型简介

HJC 本构模型包括屈服面方程、状态方程和损伤方程。屈服面方程通过无量纲等效应力描述，用于控制材料单元形状的改变。状态方程表示材料承受的静水压力与体积应变之间的关系，由弹性区、破碎区和压实区3 部分组成，用来描述材料单元在高压下的体积改变。损伤方程以等效塑性应变和塑性体积应变的累积来表示。该本构模型共包含21 项参数，本文中将这些参数分为基础物理参数、屈服面参数、状态方程参数、损伤参数和软件参数，并结合相关试验及文献结论进行参数确定。

1.2 基础物理参数

基础物理参数主要通过UHPC 基本物理试验获得，其中最大拉伸静压力T=7.12 MPa，单轴抗压强度σc=105 MPa，剪切模量G=20.37 GPa，混凝土密度ρ=2.67 g/cm3。

1.3 屈服面参数

当不考虑应变率影响时，屈服面方程转化为静态失效面方程：

式中： σ 为无量纲等效应力，A为归一化内聚力强度，B为归一化压力硬化因子，p为无量纲静水压力，D为混凝土损伤程度参数，N为压力硬化指数。在静载过程中混凝土达到最大强度，材料经历了弹性阶段和屈服阶段，由于内部孔洞被压缩，混凝土已产生部分损伤。张若棋等[20]通过混凝土单轴压缩失效强度得到失效时的损伤度D=0.659 4，并推广到一般情况。但该结果是由48 MPa 混凝土的A、B、N值推导而来，不适用于UHPC。试验测得UHPC 的峰值应变约为0.004，与普通混凝土相近，但UHPC 密度大，孔隙率较低，因而达到峰值应力时的损伤程度较普通混凝土低。根据文献[21]中的UHPC 循环压缩试验得出超高性能混凝土的失效应变为0.018 1，屈服时的等效塑性应变约为0.001 6，进而推算出屈服时混凝土材料的损伤度D=0.090 0。通过三轴等拉强度[22]fttt=0.9ft、单轴抗压强度和文献[23]给出的一组等强度UHPC 三轴围压数据，计算得出相应的归一化等效应力和归一化静水压力。将得到的3 组数据和已确定的D值代入式(1)中，得到方程组：

求解方程组，得到A=0.232 8。为了使确定的屈服面方程满足一般情况，将A、D的取值代入式(1)，根据三轴围压数据[23]进行曲线拟合，如图1所示，得到参数B=1.744 3，N=0.705 1。

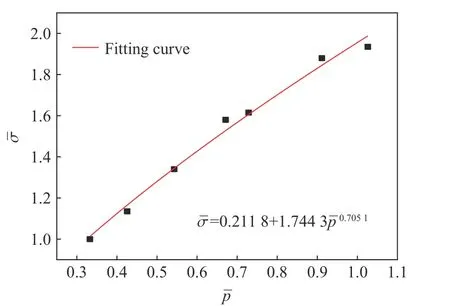
图1 静态失效强度与静水压力之间的关系Fig. 1 Relationship between static failure strength and hydrostatic pressure

应变率系数C由静态抗压强度和动态抗压强度计算得到。通过SHPB 试验得到不同应变率下C120UHPC 的抗压强度，如表1 所示。在动态荷载作用下，材料强度的提高受应变率效应和静水压力共同影响，在确定参数C时，首先要消除静水压力的影响。如图2 所示， 从-T(1-D)出发，与表1 中的数据点相连，分别作不同应变率下的直线，其中T为无量纲最大拉伸压力。过p=1/3 处作垂直于横轴的直线并与不同应变率下的直线相交于4 个点。取各交点的归一化等效应力和相应的应变率数据进行线性拟合，并作σ 与ln ( ε˙/ε˙0) 的关系曲线，其中 ε˙ 为材料真实应变率， ε˙0为参考应变率。如图3 所示，所拟合直线的斜率为应变率系数C，即C=0.003 6。

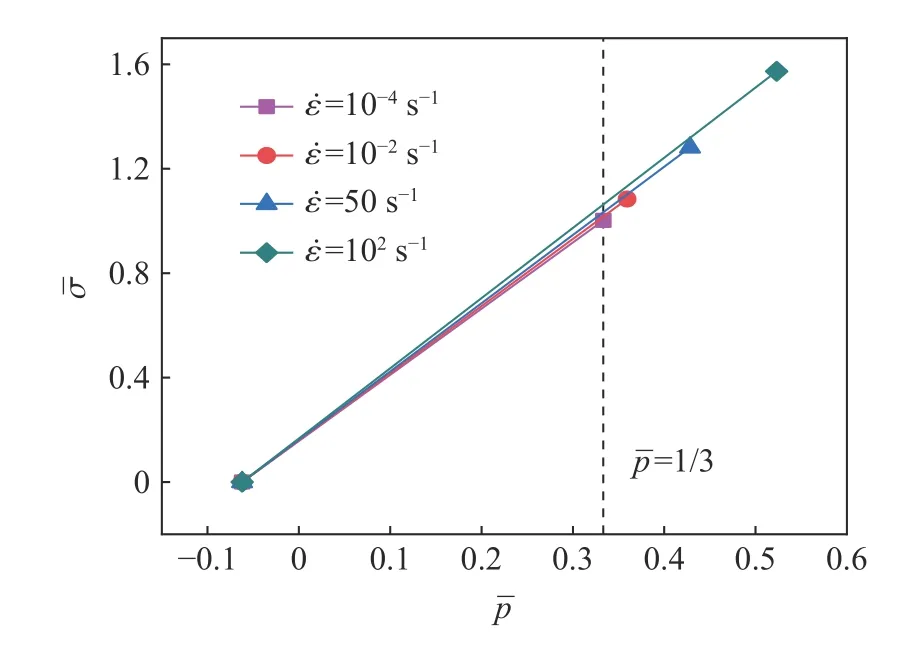
图2 不同应变率下的等效应力与静水压力之间的关系Fig. 2 Relationship between the effective-stress and hydrostatic pressure under different strain rates

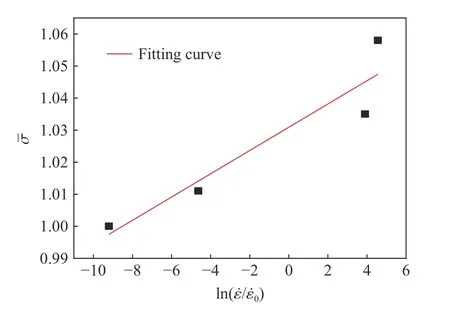
图3 UHPC 单轴抗压强度与应变率之间的关系Fig. 3 Relationship between uniaxial compressive strength and strain rate of UHPC

表1 不同应变率下的UHPC 力学参数Table 1 UHPC mechanical parameters under different strain rates

Sfmax表示归一化等效应力所能达到的最大值。在大多数的参数敏感性分析中[24-27]，该参数为不敏感参数，因此对该参数延用原始数据7.0。

1.4 状态方程参数

状态方程中弹性区和破碎区之间的过渡点静水压力表示为：

式中：pc为状态方程中弹性区和破碎区之间的过渡点静水压力，根据式(3)计算得出pc=35 MPa。

通过物理试验得到混凝土弹性模量E=50 GPa，泊松比ν=0.227。根据弹性理论计算出体积模量Ke=30.525 GPa，图4 给出了状态方程的p-µ关系曲线，由p-µ曲线关系可以计算出弹性阶段的曲线斜率，即µc=0.001 1。

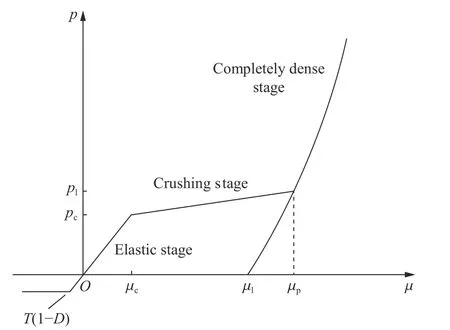
图4 HJC 本构模型状态方程Fig. 4 HJC constitutive model equation of states

µl为混凝土内部空隙被压实时的体积应变，在混凝土材料中该值与材料孔隙率相同。胡志豪[28]通过压汞试验得到相似配比UHPC 的孔隙率为3.83%，即µl=0.038 3。

K1、K2、K3为状态方程中压实段参数。相应的表达式为：

在大多数模拟中，对压力常数采用原始数据，但原始参数值过高地估计了混凝土压实后的抗体积变形能力[29-30]，需要重新确定。状态方程参数主要根据Hugoniot 试验数据[31-34]确定，目前UHPC 在这方面的试验较少，蒋国平等[35]通过气炮试验给出了C100 混凝土状态方程的压力参数：K1=46.4 GPa，K2=-195.0 GPa，K3=416.6 GPa。相比48 MPa 混凝土，C100 高强混凝土的抗体积变形能力与C120UHPC 更接近，这里采用以上参数作为C120UHPC 的状态方程参数。

从图4 看出，pl是破碎段曲线与压实段曲线交点处的纵坐标。由于压实段函数已经确定，下面只需求出破碎段曲线方程，通过求解方程组可以得到交点处坐标(µp,pl)，其中µp为pl对应的体积应变。在状态方程破碎段中，混凝土体积应变满足µc≤µ≤µp。基于静水压力实验[23]，获取上述体积应变范围内的静水压力数据，拟合第2 阶段函数表达式。在拟合过程中严格要求曲线过起始点(µc,pc)，以确保三段式函数的连续性，拟合结果为：

将已确定的K1、K2、K3、µl代入式(4)，得到第3 阶段表达式。联立式(5)和第3 阶段表达式，求解方程组，得到µp=0.043 7，pl=235.0 MPa。

1.5 损伤参数

损伤常数D1、D2与混凝土强度无关[8]，在缺少试验数值的情况下可以取原始数据，即D1=0.04，D2=1。εefmin为最小断裂应变，根据文献[21]的结论，取εefmin=0.018 1。

1.6 软件参数

参数 ε˙0用于消除应变率的量纲，其原始数值取为1 s-1，在模拟中取1～105s-1发现各项指标的模拟结果差异不大，因此对该参数延用原始数据1 s-1。

fs用于控制混凝土的失效模式，根据孙其然等[36]提出的假设，fs满足：

式中：pmax为混凝土达到极限密度ρmax时的归一化静水压力，T为无量纲最大拉伸压力。林琛等[37]假设极限密度为压实密度的1.01 倍，据此推算出ρmax=2.80 g/cm3，与之对应的体积应变µmax=0.048 7。将µmax和已确定的参数代入式(4)，计算得出pmax=445.6 MPa，结合式(6)得到fs=0.172 5。如表2 所示，超高性能混凝土HJC 本构模型参数全部确定。

表2 超高性能混凝土HJC 模型参数Table 2 HJC model parametrs of UHPC

2 模拟验证

确定了UHPC 的HJC 本构模型参数，即可通过模拟UHPC 单向板抗爆试验来验证参数的合理性。

2.1 试验工况

试验中采用临空板爆炸的形式，UHPC 单向板试件尺寸为1 800 mm×400 mm×120 mm，炸药采用TNT，当量为4.9 kg。将炸药尽量捆绑为立方体形状，置于试件中心正上方。起爆点为炸药中心，距离板的上表面跨中1.5 m 处，起爆方式为中心起爆。试验传感器布置如图5(a)所示，在UHPC 单向板跨中和支点上表面分别固定2 个压力传感器，用来测量所在位置的反射超压p1和p2。在跨中位置下表面两侧布置位移传感器，用来测量单向板跨中挠度。

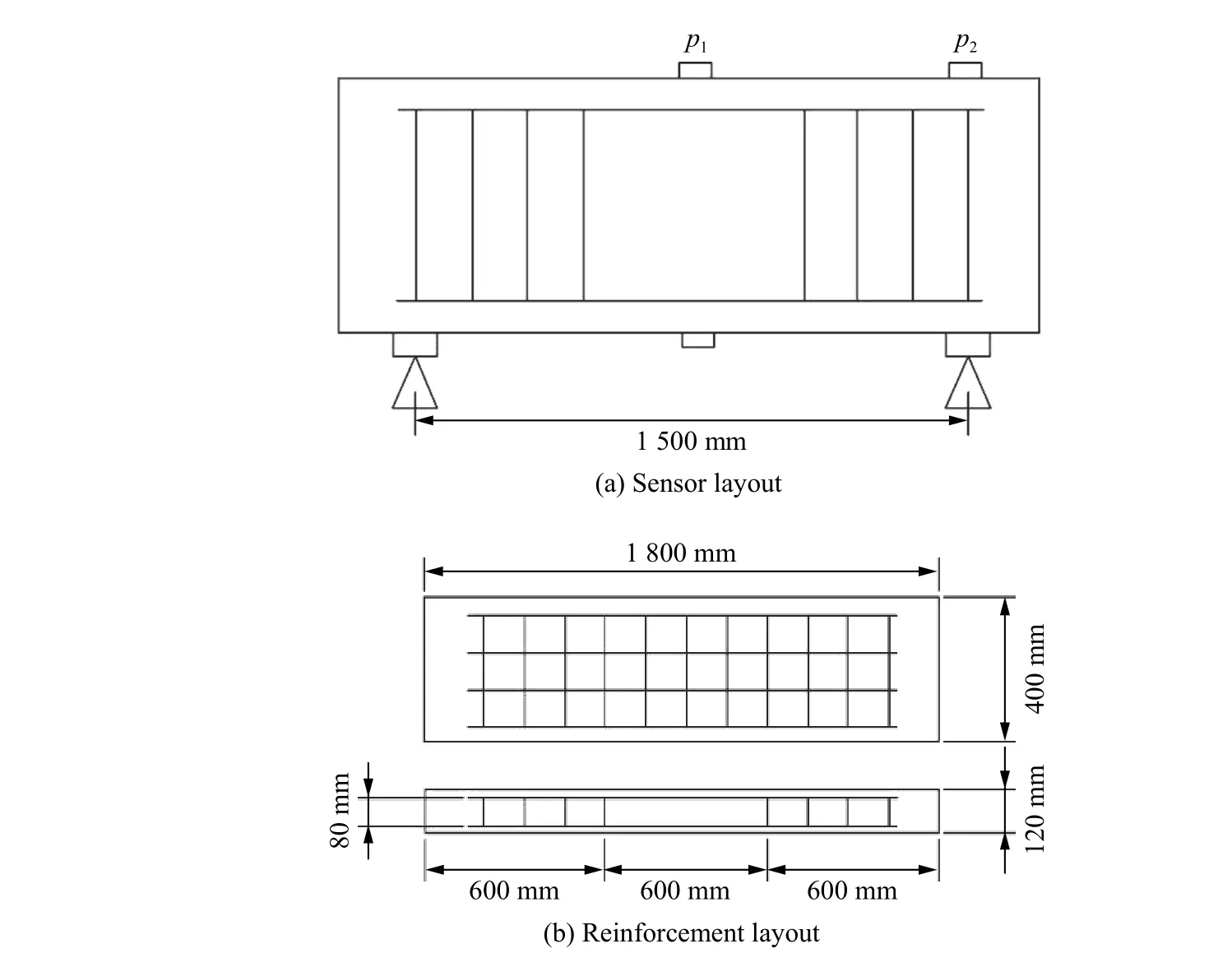
图5 试验工况Fig. 5 Test layout

单向板试件采用4 根直径为8 mm 的受拉钢筋，钢筋级别为HRB500，保护层厚度为20 mm，受拉纵筋配筋率为0.52%。试件中箍筋采用HRB400 级钢筋，单向板的配筋见图5(b)。

2.2 模型建立

利用LS_DYNA 软件对爆炸工况进行数值模拟。如图6 所示，建立1/2 模型，在对称面上施加法向约束，空气四周设置透射边界。在混凝土的一侧建立刚性、全约束支撑，混凝土材料选择HJC 模型，材料取值见表2。钢筋材料选择线性强化模型MAT_PLASTIC_KINEMATIC_TITLE，该模型对于爆炸荷载作用下的金属材料非常适用[38]。材料参数由钢筋拉伸试验测得，取值如表3 所示。在爆炸作用下，构件中的应力波作用时间极短，钢筋和混凝土之间可以按变形一致处理[39]。因此，对钢筋和混凝土采用共节点方式建立联系。分析使用流固耦合算法，炸药和空气采用Euler 网格，钢筋混凝土板采用Lagrange 网格，其中总单元数为243 000，节点数为261 000。

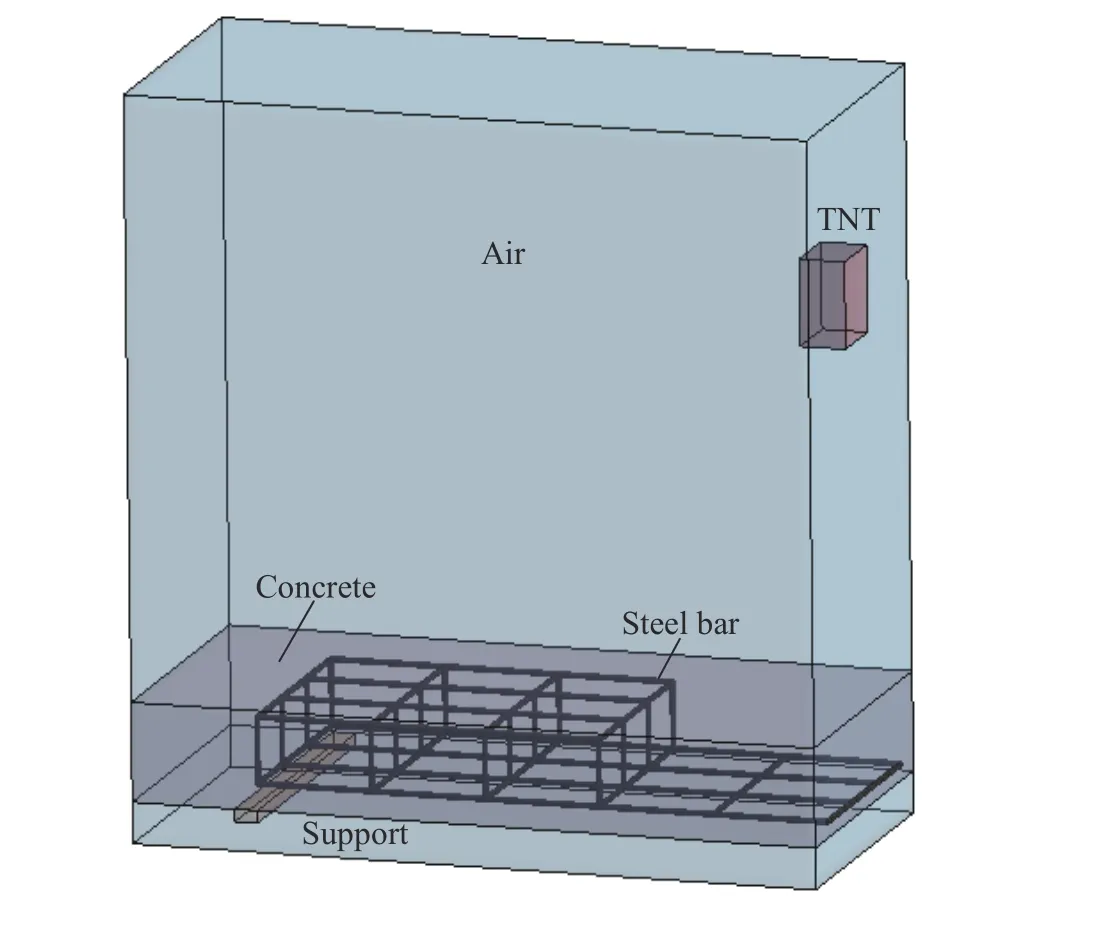
图6 有限元模型Fig. 6 Finite element model

表3 钢筋本构模型参数Table 3 Parameters of reinforcement constitutive models

2.3 结果分析

试验中，由于药量较大，未能测得跨中反射超压p1，仅测量了支座处的反射压力。p2的平均测试结果为7.20 MPa，模拟值为7.40 MPa，误差为2.7%，表明模拟加载过程相对可靠。从毁伤结果可以看出，试件完整性较好，顶部未见严重破坏，其破坏主要体现为单向板底部开裂和侧面的裂缝开展。这是因为，爆炸产生的冲击波在靶板迎爆面形成超压破坏，当应力波传递到板下表面并反射形成拉伸波对靶板造成拉伸破坏，而UHPC 的拉压抗性的不同造成背爆面产生更严重的损伤。在数值模拟中，仅对原始参数[8]中的基本物理参数（抗压强度、最大拉伸静压力、剪切模量和密度）进行修改，以此作为修正前的原始参数，如表4 所示。将已确定的HJC 模型参数作为修正后的UHPC 参数，并将模拟结果与试验结果进行比较。当计算到7 ms 时，单向板变形达到最大并开始出现回弹现象，这时累积塑性损伤阶段基本结束，因此计算时间采用7 ms。

表4 修正前的原始参数Table 4 Original parameters before correction

等效塑性应变可以直接、定量地反映材料的变形毁伤程度[40]。图7 给出了不同参数下的等效塑性应变云图。从图7 可以看出，在修正前的原始参数模拟结果中，单向板的迎爆面在中心出现少量损伤，而在背爆面中部没有出现损伤，其背爆面的损伤程度远小于迎爆面，与试验结果相悖。在修正后的UHPC 参数模拟结果中，单向板迎爆面出现轻微塑性破坏，在背爆面中部出现较大范围的塑性损伤并向板两侧延伸，模拟出了拉伸应力波对板的破坏效果。其背爆面的破坏程度大于迎爆面，符合实际情况。观察单向板侧面，参数修正前没有出现破坏现象。参数修正后，呈现出了由中部向两侧斜向延伸的损伤带，类似于斜拉破坏特征。由此可知，修正后的UHPC 参数对试件侧面斜裂缝的描述也与试验基本接近。

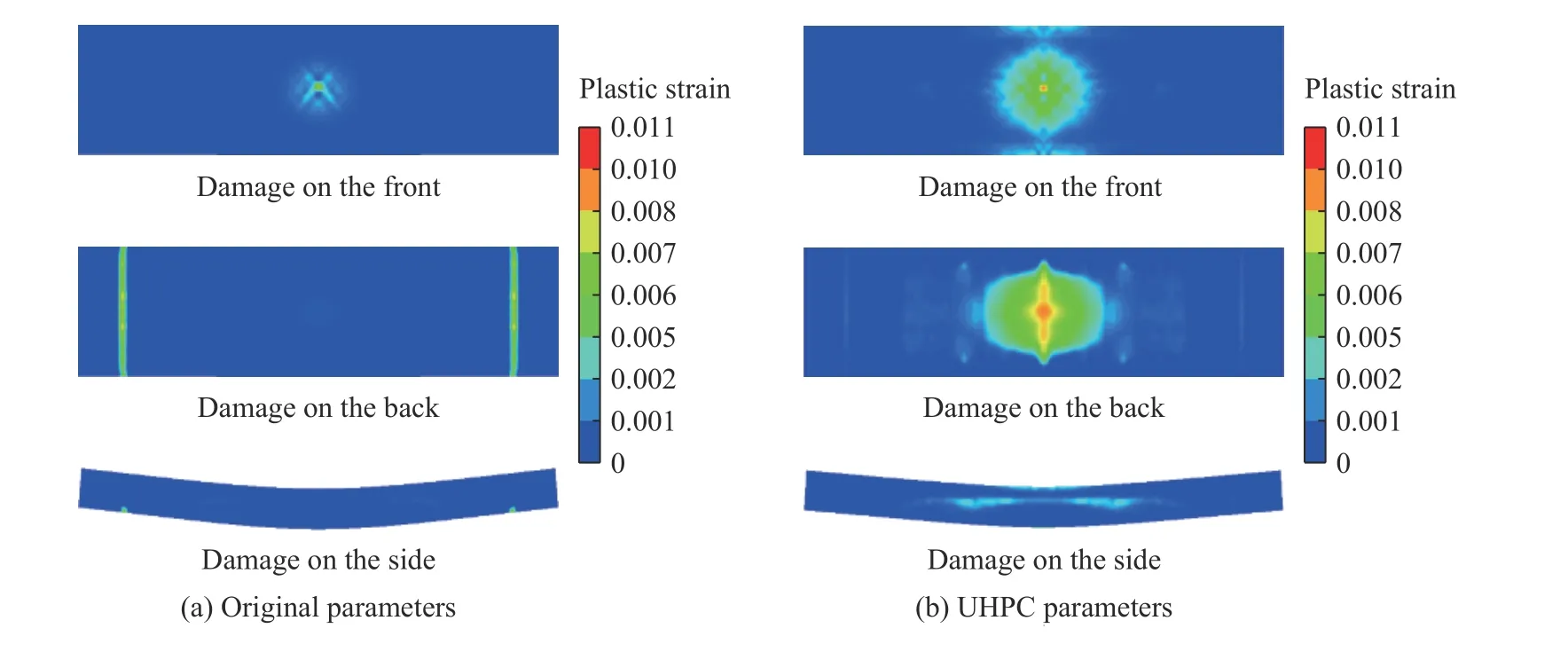
图7 不同材料参数下的塑性损伤模拟效果对比Fig. 7 Comparison of simulation effects of plastic damage under different material parameters

通过位移传感器，测得单向板的最大挠度为42.80 mm。图8 为修正前的原始参数和修正后的UHPC 参数的位移时程曲线。参数修正前的计算结果显示，板的最大挠度为53.86 mm，误差为25.8%。参数修正后的计算结果显示，板的最大挠度为41.14 mm，误差为3.9%，与试验基本一致。

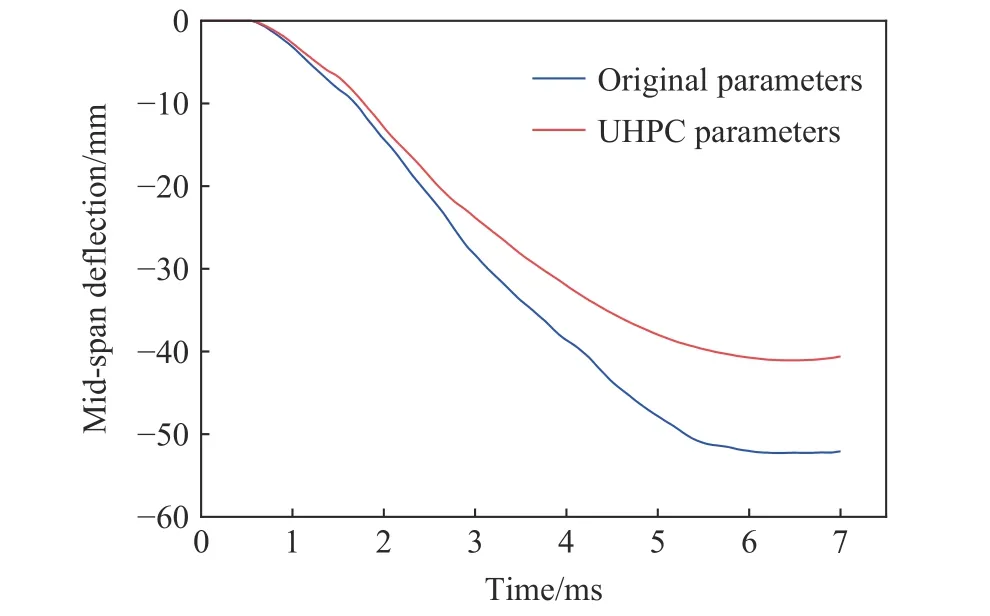
图8 不同材料参数下跨中挠度的时程曲线Fig. 8 Time history curves of mid-span deflection under different material parameters

综上，在爆炸工况下， 修正后的UHPC 参数对单向板的跨中最大挠度和毁伤程度的描述更接近试验结果。表2 给出的本构模型参数可以初步作为超高性能混凝土的HJC 本构模型参数。

3 超高性能混凝土HJC 本构模型应用

3.1 配筋对UHPC 单向板抗爆性能的影响

图5 的试验工况中，当混凝土板达到最大挠度时，钢筋的等效塑性应变和等效应力分布如图9 所示。从纵向钢筋的受力情况可以看出，底部中央的纵筋应力最大且出现塑性应变，端部上表面纵向钢筋的应力比下表面低且整体应力水平较低，基本没有产生塑性应变。说明构件在底部中央受到较大拉伸变形，其纵筋在受拉过程中达到屈服，起到了很好的耗能作用。构件端部受爆炸影响相对较小，其纵筋未达到屈服且上部钢筋的利用率更低。观察箍筋受力情况，发现底部中央的横向钢筋受力最大并出现轻微塑性变形，垂直于混凝土上下表面的钢筋也承受一定荷载，但并未发生屈服。说明在构件底部中央的横向拉伸变形较小，在构件两端有剪切破坏的趋势，因此箍筋中产生的拉应力起到了一定的作用。

图9 1/2 模型的钢筋塑性应变和等效应力分布Fig. 9 Distributions of plastic strain and equivalent stress of reinforcement in the 1/2 model

为了提高钢筋的利用率，应对底部受拉纵筋采用较高级别的钢筋，上部纵向钢筋和箍筋可以采用低级别的钢筋。为了进一步了解钢筋对UHPC 单向板抗爆性能的影响规律，通过数值模拟来对比不同箍筋间距、纵筋配筋率下的单向板跨中最大挠度和板侧面斜裂缝长度。模型工况为在图5 基础上采用上下双层配筋，对箍筋和上部纵筋使用HRB400 级钢筋，对底部纵筋使用HRB500 级钢筋。其中纵筋配筋率r分别为0.26%、0.52%、0.92%，箍筋间距d分别为75、150、300 mm。

图10 为不同箍筋间距下跨中最大挠度与配筋率的关系，可以看出，单向板跨中最大挠度随主筋配筋率的增加而减小，减小幅度近似呈线性。当主筋配筋率不变，减小箍筋的间距时，板的挠度最大值变化小于2 mm，变化不大。表明主筋的配筋率对跨中最大挠度的变化更敏感，提高配筋率可以提高单向板底部的受拉承载力，而加密箍筋对板跨中最大挠度影响较小。

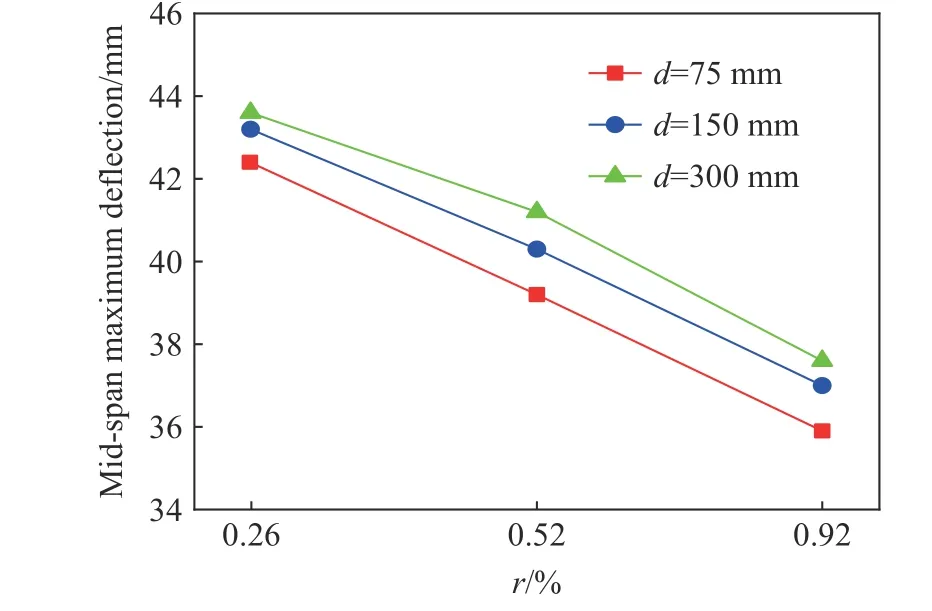
图10 不同箍筋间距下跨中最大挠度与配筋率的关系Fig. 10 Relationship between mid-span maximum deflection and reinforcement ratio under different stirrup spacings

图11 为不同配筋率下斜裂缝长度与箍筋间距的关系，可以看出，单向板侧面斜裂缝长度随箍筋间距减小而减小，当箍筋间距处于150～300 mm 时，箍筋的作用效果减弱。主筋配筋率的提高也会在一定程度上抑制斜裂缝的增长，并且增强箍筋的作用效果。当箍筋间距为300 mm 时，主筋对斜裂缝的扩展几乎没有影响，随着箍筋的不断加密，主筋的影响效果也在增强。

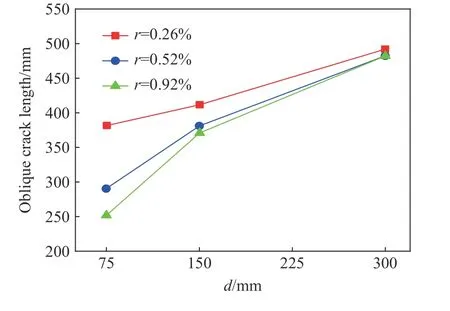
图11 不同配筋率下斜裂缝长度与箍筋间距的关系Fig. 11 Relationship between oblique crack length and stirrup spacing under different reinforcement ratios

以上现象表明，加密箍筋可以有效抑制斜裂缝的扩展，提高UHPC 单向板的抗剪承载力，但提高效率会出现下降拐点。主筋配筋率的提高也会对箍筋的作用效果起到辅助作用。

3.2 单向板尺寸对UHPC 抗爆性能的影响

根据单向板的设计要求，在试验板的基础上分别对板的长、宽、厚度尺寸进行调整。变化某一方向尺寸时，保持另外2 个方向尺寸不变，对单向板的长、宽、厚度各取3 个尺寸进行模拟计算，尺寸变化如表5 所示。通过比较不同尺寸下的单向板跨中最大挠度、斜裂缝长度及迎爆面和背爆面的毁伤面积，得到尺寸变化对UHPC 单向板抗爆性能的影响规律。爆炸工况采用图5 试验工况，由于只考虑混凝土影响，不建立钢筋模型。毁伤面积根据塑性应变值确定，根据UHPC 单轴循环试验结果[21]，分析当塑性应变累积到0.002 时，UHPC 材料出现明显的破裂现象，因此以该塑性应变作为毁伤界限。

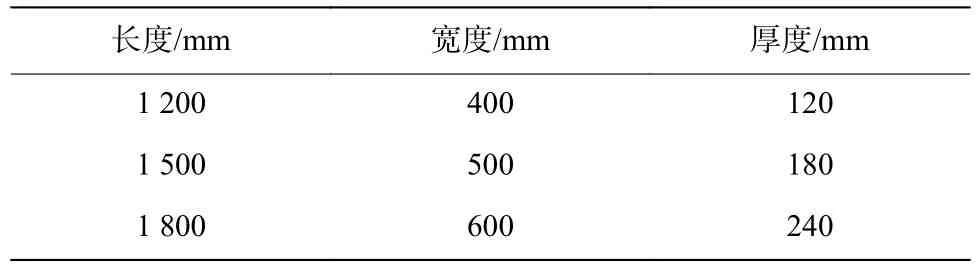
表5 单向板各方向尺寸变化Table 5 Dimension change of one-way plate in each direction

图12 给出了爆炸工况下UHPC 单向板尺寸变化的影响规律。从图12(a)可以看出，单向板长度增加会引起迎爆面和背爆面的毁伤范围增大，当单向板长度为1 500～1 800 mm 时，迎爆面的毁伤范围不再变化，而背爆面损伤范围仍在增加。单向板的裂缝长度以及跨中最大挠度也随着长度的增加而增加，这表明，UHPC 单向板长度变化与构件破坏程度成正相关。从图12(b)可以看出，单向板的宽度增加同样引起迎爆面和背爆面的毁伤面积增加，当宽度为500～600 mm 时，迎爆面和背爆面损伤出现相反的变化趋势，其中背爆面损伤面积的增长速率呈下降趋势。随着宽度的增加，斜裂缝长度和跨中最大挠度均出现下降，且当宽度为500～600 mm 时，斜裂缝不再变化，跨中最大挠度的下降速率有所降低。这是因为，板宽度的增大使横截面惯性矩成倍增大，从而导致截面抗弯性能增强，但在此宽度范围内，板出现纵向的轻微弯曲，对横向弯曲变形起到了抑制作用。单向板宽度的增大使靶板的受力面积增大，从而导致迎爆面和背爆面的破坏范围也有所增大，这不足以说明板的毁伤程度增大。综合考虑，UHPC 单向板的宽度变化与构件破坏程度成负相关。由图12(c)可知，当单向板厚度增大时，各项破坏指标均大幅度降低。当厚度为180～240 mm 时，最大挠度的下降速率变缓，斜裂缝长度的下降速率变大。可以看出，截面的惯性矩呈指数形式增长，大幅度提高了横截面的抗弯刚度，从而减小跨中挠度。而增大UHPC 单向板厚度可以有效抑制爆炸工况下的斜裂缝扩展现象。对3 种尺寸效应进行横向对比可以发现，相比迎爆面，单向板的背爆面毁伤面积对尺寸变化更敏感，这从侧面反映了UHPC 抗拉、压能力的不同。在3 种尺寸效应中，通过各指标变化范围与尺寸变化之比来衡量尺寸效应的影响程度，容易看出，计算结果对厚度变化的敏感程度最高，对长度次之，对宽度变化的敏感程度最低。

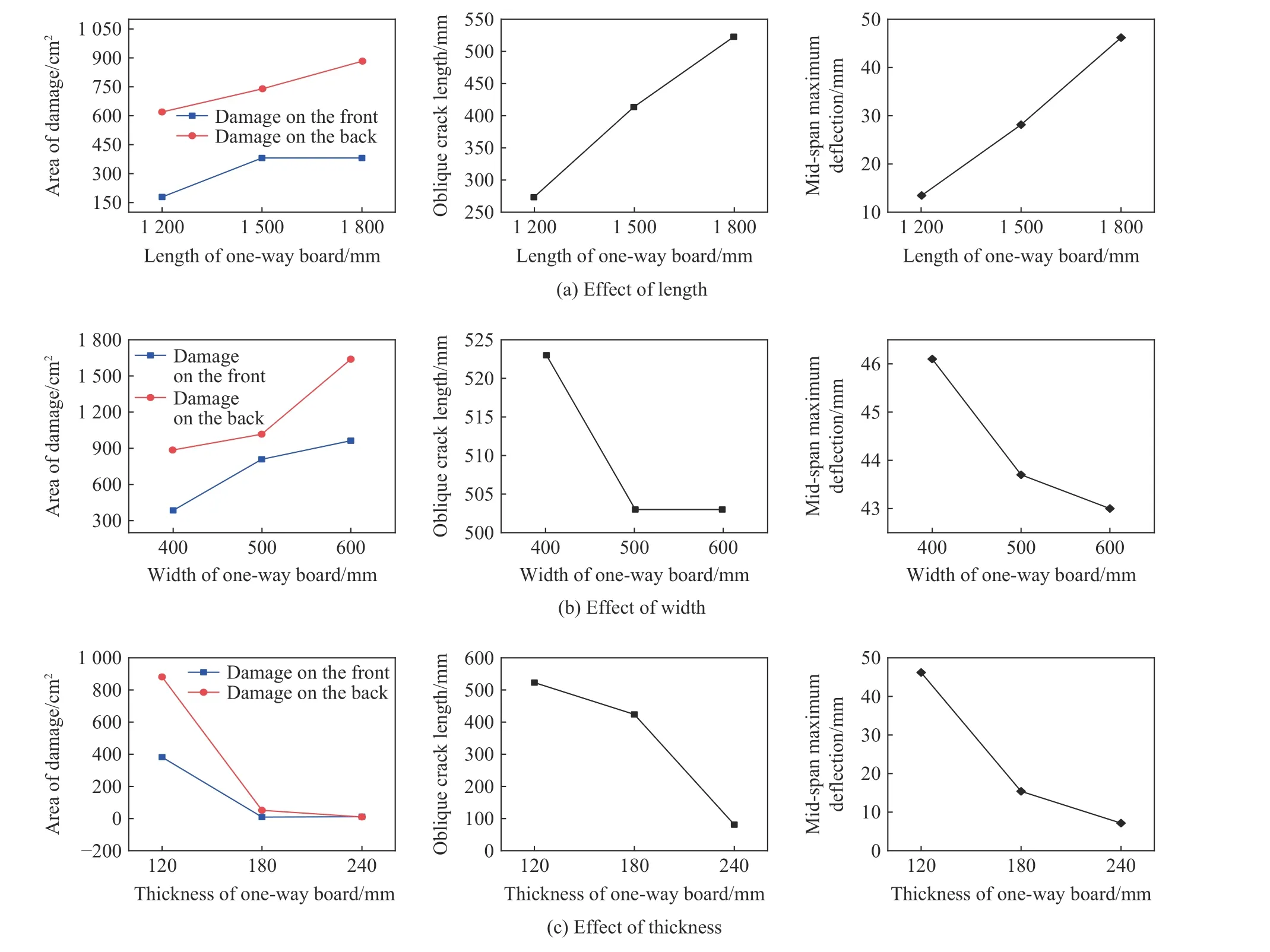
图12 单向板的尺寸效应Fig. 12 Dimension effects of the one-way slab

4 结 论

基于超高性能混凝土力学试验及单向板数值模拟分析，得出以下主要结论。

(1) 得到一组超高性能混凝土的HJC 本构模型参数。通过与超高性能混凝土单向板爆炸试验结果进行对比，验证了参数的有效性。

(2) 在临空板爆炸工况下，提高超高性能混凝土单向板的主筋配筋率，可以有效降低板的跨中最大挠度，并且可以促进箍筋的作用效果。加密箍筋可以提高单向板的抗剪承载力，抑制斜裂缝扩展，对跨中挠度的减小也有一定效果。在配筋时，单向板上部纵筋和箍筋可采用低级别钢筋，底部纵筋宜采用较高级钢筋。

(3) 在临空板爆炸工况下，超高性能混凝土单向板有明显的尺寸效应。其中毁伤程度随板长度增大而升高，随板宽度和厚度增大而降低。在不同尺寸效应中，爆炸计算结果对单向板厚度变化最敏感，对长度次之，对宽度变化的敏感程度最低。