水下爆炸对重力坝的毁伤效应及最优爆距*

黄谢平，孔祥振，陈祖煜，方 秦

（1. 浙江大学岩土工程研究所，浙江 杭州 310058；2. 陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007）

水工大坝因其重要的政治、经济意义，在战争中是强敌重点打击的目标。海湾战争后的几场高技术局部战争表明，常规武器已成为强敌打击的主要手段。近年来，强敌常规武器向深侵彻、大当量和高精度方向发展，如美军列装的MOP 巨型钻地弹GBU-57 重达14 t，装药量2.7 t，由B-52 或B-2 轰炸机投放，通过惯性和GPS 制导，精度误差1.2 m，这给军事、民用建筑的防护带来前所未有的挑战。对大坝而言，根据弹体是否直接命中大坝，弹体对大坝存在两种可能的打击方式：弹体直接命中大坝，以先侵彻后爆炸的方式打击大坝；弹体未直接命中大坝而落入上游水库，以水下爆炸方式打击大坝。研究表明[1]，水下爆炸产生高压、高速冲击波，对结构毁伤效应显著高于同等装药量空中爆炸，水下爆炸是大坝被攻击时所能遭遇到最极端的情况之一。在历史战争中，有不少大坝因遭遇水下爆炸打击而破坏[2-4]，造成下游公路、铁路被冲毁，带来巨大人员伤亡和财产损失。

为了减轻爆炸荷载对重力坝的破坏性灾害，大量学者通过试验和数值计算探究水下爆炸对重力坝的毁伤效应和破坏机理。试验方面，因重力坝结构尺寸较大且涉及爆炸荷载存在安全风险，原型试验几乎难以开展。值得一提的是，2020 年，军事科学院等单位利用待拆除的吉林丰满老坝开展了现场水下爆炸试验[3-4]，但相关试验结果尚未见公开报导。更多试验采用的主要是小比尺模型，且为了再现原型重力坝自重应力场，模型试验依赖于超重力离心机。例如，Vanadit-Ellis 等[5]开展了几何比尺为1/100 的重力坝水下爆炸离心模型系列试验，根据爆距、重力坝尺寸等因素，总结了三种不同的重力坝破坏模式即材料破坏、局部破坏和结构破坏。Huang 等[6-8]开展了多组重力坝水下爆炸离心模型试验并结合炸药-库水-空气-重力坝结构的全耦合数值模型，就水下爆炸冲击波荷载对重力坝的毁伤效应[6-7]和气泡脉动效应[8]开展了较为系统的研究和分析。应当指出，相关模型试验数量依然较少，更多研究成果主要通过数值计算获得。例如，Zhang 等[9]和王高辉等[10]探究了冲击波荷载下重力坝的破坏模式和毁伤机理。Li 等[11]分析了不同库水位下重力坝非线性动力响应的差异并建议战时提前降低库水位以减少爆炸荷载对重力坝的破坏性灾害。Wang 等[12]建立数值模型分析了重力坝自重应力场对其动力响应的影响。注意到水下爆炸在结构附近因反射波和入射波相互抵消而产生局部空化效应导致附近水域压力降低甚至产生负压，Zhang 等[13]通过数值计算分析了负压力在重力坝结构响应中的影响，指出了考虑局部空化效应的必要性。为了模拟弹体直接命中大坝的情况，Shu 等[14]通过重启动分析研究了重力坝经历先侵彻后爆炸的破坏模式和破坏机理。Zhu 等[15]对比分析了LS-DYNA 中的全耦合模型和ABAQUS 中的半耦合模型在重力坝水下爆炸领域的表现，认为全耦合模型更适用于近场水下爆炸的情况。此外，有不少研究关注大坝毁伤程度的评估方法，提出了基于损伤面积[16-17]、大坝频率数据库[18]以及大坝最优振动特性[19]的评估方法。这些研究极大丰富了我们对重力坝水下爆炸问题的认识。

注意到随着弹药起爆时与重力坝距离（即爆距）的不同，水下爆炸对重力坝的毁伤效应及重力坝的破坏程度存在显著差异。已有研究普遍认为，随着爆距增加，水下爆炸对重力坝的毁伤效应降低。例如，Zhang 等[9,20]通过数值分析认为，随着爆炸距离的增大（比例爆距范围为0.74～2.24 m/kg1/3），水下爆炸冲击波峰值压力逐渐减小，重力坝动力响应减弱，破坏范围变小；张启灵等[21]基于数值计算结果得到随着爆源距离的增大（比例爆距范围为2.71～8.14 m/kg1/3），相同装药量爆炸对重力坝的损伤作用显著减小，表现为坝体中断面损伤比例显著减小；Wang 等[22]根据爆距和炸药量的不同对重力坝损伤程度进行归类并建立了拟合公式，该拟合公式同样表明，随着爆距增加（比例爆距范围为0.2～6.46 m/kg1/3），水下爆炸冲击荷载对重力坝损伤程度降低；Ren 等[16]则采用大坝缺口面积评估大坝在水下爆炸荷载下的破坏程度，结果表明，随着爆距增加（比例爆距范围为0.69～6.5 m/kg1/3），大坝缺口面积呈现下降趋势。

应当指出，水下爆炸荷载下，重力坝毁伤程度一方面取决于水下爆炸荷载强度，另一方面则依赖于重力坝的响应机理和破坏机制。已有研究注意到水下爆炸冲击波荷载随着爆距增加而衰减且主要关注重力坝局部响应和局部破坏，从而普遍认为随着爆距增加，水下爆炸对重力坝的毁伤效应降低，而忽视了重力坝响应机理和破坏机制的影响。不同于重力坝局部响应和局部破坏，在重力坝整体结构破坏机制下，例如，对于水下爆炸荷载下重力坝整体弯曲导致的拉伸破坏机制[6-8]，当爆距过小时，水下爆炸荷载过于集中，作用面积小，对重力坝产生的整体弯矩反而更小；相反，适当增大爆距，保证水下爆炸冲击波荷载强度较高的同时又使得该荷载能够向重力坝坝顶和坝底传播，作用面积更大，对重力坝产生的整体弯矩反而更大。因此，在重力坝整体结构破坏机制主导下，适当增加爆距，水下爆炸对重力坝的毁伤程度甚至比小爆距时更严重，即水下爆炸对重力坝的毁伤效应可能存在“最优爆距”。

本文利用超重力离心模型试验[6-8]，建立炸药-库水-空气-重力坝结构的全耦合数值模型，对比分析不同爆距水下爆炸对重力坝的毁伤效应。设计5 组不同爆深、每组爆深对应12 组不同爆距共60 组数值计算工况，所有工况水深、炸药量以及重力坝模型相同；为了明确是否存在“最优爆距”，对比分析相同爆深不同爆距水下爆炸对重力坝的毁伤程度，并定量比较上游坝面损伤面积占比、上游坝面损伤区域的平均损伤、大坝单元删除率、坝踵最大拉应力平均值、坝踵最大拉应变平均值等参数。

1 数值模型

1.1 炸药-库水-空气-重力坝结构的全耦合数值模型

重力坝水下爆炸是个多学科交叉的复杂问题，涉及炸药在水中的起爆，水下爆炸冲击波、气泡脉动等主要物理过程，以及水库动水与重力坝结构的相互作用即流固耦合和重力坝的非线性动力响应等问题。本文基于超重力离心模型试验[6-8]，采用CLE (coupled Lagrangian-Eulerian) 方法建立了炸药-库水-空气-重力坝结构的全耦合数值模型（如图1 所示），并对重力坝水下爆炸开展全过程数值模拟研究。炸药、水和空气采用Eulerian 网格建模，坝体结构和模型箱采用Lagrangian 网格建模。考虑到试验中该模型的对称性，数值建模时采用了1/2 对称模型，并在对称面上施加了对称边界。为了模拟试验中铝制模型箱对库水的约束，在数值建模时也考虑了该模型箱。为了模拟真实重力坝的动力响应，开展离心模型试验和数值建模时，重力坝模型由三个完全相同的重力坝坝段组成，三个坝段并排布置、相互独立。每个坝段宽235 mm，高550 mm，图1 右给出了重力坝坝段的详细几何尺寸并且标记了中间坝段和左边坝段的对称轴线1 和线2，便于后续2.4 节的分析。炸药量、水深、爆深和爆距等参数将在1.4 节数值计算方案中给出。在超重力离心模型试验中，整个模型受到80g的离心加速度[6-8]。为了模拟该离心加速度，在炸药引爆前，通过LS-DYNA 软件中的动力释放法对整个数值模型施加了G=80g的重力加速度。为了保证计算精度同时提高计算效率，通过网格敏感性分析[7-8]，该有限元模型的网格尺寸确定为6 mm。

图1 炸药-库水-空气-重力坝结构的全耦合数值模型及大坝尺寸Fig. 1 Numerical model of the fully coupled explosive-water-air-dam system and dam dimension

1.2 混凝土本构模型

在本文的数值研究中，采用Huang 等[23]近期提出的混凝土流体弹塑性模型描述重力坝的动力响应。Huang 等模型通过引入混凝土自由水效应[24-25]在Kong-Fang 混凝土模型[26]基础上发展而来。

Huang 等模型中混凝土材料的偏应力行为通过最大强度面σm和残余强度面σr定义，即

式中：p为静水压力；Dtot为总损伤；w为相对自由水含量，介于0 到1 之间，其具体定义见文献[23]；fc(w)和分别为混凝土相对自由水含量为w时的准静态单轴压缩和单轴拉伸强度;ψ 是拉伸子午线与压缩子午线的比值；a1和a2为混凝土材料参数；p0为混凝土毛细管孔隙完全坍缩时的压力阈值。对于饱和混凝土，相对自由水含量w=1.0，p0=130 MPa[23]。当前失效面Y定义为

式中：r′为当前子午线与压缩子午线的比值，与混凝土材料的Lode 角效应有关。屈服面f的表达式为

式中：J2为偏应力张量第二不变量。采用径向放大法引入应变率效应，则当前失效面Y放大为

式中：rf为动态增长因子，定义为材料在高应变率加载时动态强度与准静态加载时准静态强度的比值。在Huang 等模型中，动态增长因子的定义为[27]

式中： ε˙ 表示应变率。干燥混凝土ηt定义为[28]

式中：Fm=10，W1=1.6，S=0.8，W2=5.5，均为无量纲拟合参数； ε˙0=1 s-1，为相对应变率。

在Huang 等模型中，采用Kong 等[26]提出的改进等效塑性应变λ 定义损伤的累积即

式中：λc和λt分别为改进后的等效压缩和拉伸塑性应变， Δ ε¯p为有效塑性应变增量，Δ ε¯1为单轴拉伸下塑性应变增量，d1和d2是无量纲损伤参数。

拉伸损伤Dt定义为

式中：εfrac为断裂应变；c1=3，c2=6.93，为无量纲材料参数。

压缩损伤Dc定义为

总损伤Dtot定义为

在Huang 等模型中，状态方程为

式中：ptot为饱和混凝土承受的总压力，由干燥固体骨架承担的部分pdry和混凝土毛细管孔隙中自由水承担的部分pw组成；系数b用以调控自由水部分的贡献，对于饱和混凝土，b的建议值为0.5[25]。pdry将采用商业软件LS-DYNA 中已有的状态方程，即

式中：µ为体应变，E0为单位体积的初始内能，h0为比热率，q(µ)和θ(µ)分别是压力函数和温度函数。自由水承担的部分pw采用Grüneisen 状态方程描述，即

式中： µ¯=µ-µ0，µ0为压力阈值p0对应的体应变；E为单位体积的内能；C为粒子速度曲线的截距；S1、S2和S3为粒子速度曲线的斜率参数；ρ0为水的初始密度；γ0为Grüneisen 系数；α 为对γ0的一阶体积修正。对于水而言，ρ0=1 000 kg/m3，C=1 480 m/s,S1=2.56，S2=1.986，S3=1.226 8，γ0=0.35，E=1.89 MJ/m3，α=0。

重力坝混凝土单轴压缩强度和单轴拉伸强度分别为15.2 和1.49 MPa，杨氏模量为20.1 GPa[6-8]。表1给出了Huang 等混凝土本构模型需要的其他材料参数。状态方程参数则参考文献[26]，这些参数基于材料单轴压缩强度通过Huang 等模型自带的参数自动生成程序获得。

表1 混凝土本构模型参数Table 1 Parameters required in the concrete model

通过将式(16)中 µ¯ 换成水的体应变µ就可以描述库水的状态方程。采用Jones-Wilkins-Lee 状态方程描述炸药爆炸产生的压力，即

式中：V为爆炸产物的相对体积，Ee为每单位体积炸药的内能，而A、B、R1、R2、ω 为材料参数。对于TNT 炸药[22]：A=3.712×1011Pa，B=3.231×109Pa，R1=4.15，R2=0.95，ω=0.3，Ee=7.0 GJ/m3，TNT 炸药密度ρe=1 600 kg/m3。

1.3 数值模型验证

为了获得真实可靠的数值计算结果，上述建立的数值模型应当得到充分的验证。本文基于前期开展的离心模型试验建立了炸药-库水-空气-重力坝结构的全耦合数值模型，对重力坝水下爆炸开展了全过程数值模拟研究，并将该模型预测的结果与多组离心模型试验结果进行了对比。表2 给出了3 组典型工况的离心模型试验。其中试验UE-01 和UE-02 用以探究冲击波的破坏效应，试验UE-03 爆源位于水域中心边界影响较小用以探究气泡脉动效应。图2 和图3 分别给出了UE-01 和UE-02 工况下，试验和数值预测重力坝破坏对比结果[6-7,29]。图4 和图5则给出了数值预测的气泡脉动过程以及试验、数值模拟和G&H 理论模型[30]预测的气泡周期和气泡最大半径的对比结果[8]。可以发现，数值预测结果与试验结果十分吻合，该数值模型能够准确预测水下爆炸冲击波和气泡脉动过程以及水下爆炸荷载下重力坝的非线性动力响应和破坏。相关讨论见文献[6-8, 29]，这里不再重复。

图2 数值预测的大坝破坏与离心模型试验UE-01 结果对比[6-7, 29]Fig. 2 Comparison of dam failures obtained by numerical simulations and centrifuge test UE-01[6-7, 29]

图3 数值预测的大坝破坏与离心模型试验UE-02 结果对比[6-7, 29]Fig. 3 Comparison of dam failures obtained by numerical simulations and centrifuge test UE-02[6-7, 29]

图4 数值预测气泡脉动过程[8]Fig. 4 Bubble oscillation predicted by the numerical simulation[8]

图5 试验、数值和理论预测气泡周期（Tb）和最大半径（Rbm）[8]Fig. 5 Bubble period (Tb) and maximum size (Rbm) predicted by centrifuge tests,numerical simulations, and the theoretical model[8]

表2 离心模型试验方案[6-8, 29]Table 2 Schemes of the centrifuge tests[6–8, 29]

1.4 数值计算方案

为了研究不同爆距水下爆炸对重力坝的毁伤效应，探讨是否存在“最优爆距”，本文依据前期开展的一组超重力离心模型试验UE-01 设计了数值计算方案。不同计算工况下，重力坝模型的几何比尺均为1/80，相应的重力加速度G=80g，水深Hw=600 mm，炸药量W=2.2 g。考虑到爆深不同，水下爆炸冲击波荷载对大坝形成的整体弯矩存在差异，设计了5 组不同爆深，分别为L=50, 100, 150, 200, 250 mm。为了分析爆距的影响，每组爆深对应12 组不同爆距即R=10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 150, 200 mm，对应的比例爆距范围为0.077～1.54 m/kg1/3。根据爆深和爆距的不同，总共进行60 组数值计算。

2 结果与讨论

基于上述数值计算方案，为了探讨是否存在“最优爆距”，这一小节将从重力坝破坏程度、损伤面积和平均损伤、单元删除、应力和应变四个方面定性和定量比较不同爆距水下爆炸冲击波荷载对重力坝的毁伤效应。

近场法采用势流理论，对湿单元(Wet Element)表面积分求解二阶定常力，而远场法通过动量定理来求解二阶定常力且仅能计算纵荡、横荡和艏摇三个自由度的平均波浪力。近场法的计算依赖于计算网格数量，一般情况下近场法计算有一定差距。当近场法与远场法计算结果趋势一致且误差不大时，可近似认为水动力计算网格满足要求[8]。纵荡、横荡和艏摇方向近场法和远场法二阶定常波浪力对如图3～图5所示，图线显示近场法和远场法计算结果趋势一致且误差较小，说明模型网格划分符合计算要求。

2.1 重力坝破坏

图6、图7 和图8 分别给出了50、100 和150 mm 爆深不同爆距水下爆炸冲击波荷载下重力坝的损伤云图。本文中，损伤随着不可逆等效塑性应变的增长而累积包括拉伸损伤和压缩损伤，相关定义见式(10)～(13)。图6、图7 和图8 给出的是总损伤Dtot（式(13)）的结果。本文仅关注冲击波的破坏效应，上述损伤云图为6 ms 时刻的计算结果。可以发现，3 组不同爆深下，重力坝破坏模式接近，上游坝面拉伸损伤严重，大坝破坏（以10 mm 爆距为例）都主要集中在3 个部位即坝头变截面处的整体水平断裂、中间坝段坝身处的倾斜贯穿断裂以及坝踵处的拉伸裂缝。上述破坏主要归结为水下爆炸冲击波荷载对重力坝造成整体弯矩，使重力坝整体向下游弯曲，导致上游坝面垂直方向整体处于受拉状态，即重力坝整体弯曲导致的拉伸破坏[6-8]。在这一破坏机制主导下，拉伸裂缝萌发于上游坝面并不断向下游坝面发展，最终形成坝身处的贯穿断裂以及坝踵处的未贯穿裂缝。此外，可以发现，随着爆深增加（50，100 和150 mm），中间坝段坝身处倾斜贯穿断裂的位置向坝底靠近（距坝底高度分别为0.32，0.26 和0.21 m），这是因为爆深的改变将影响上游坝面整体弯矩使得上游坝面裂缝萌发位置发生变化。

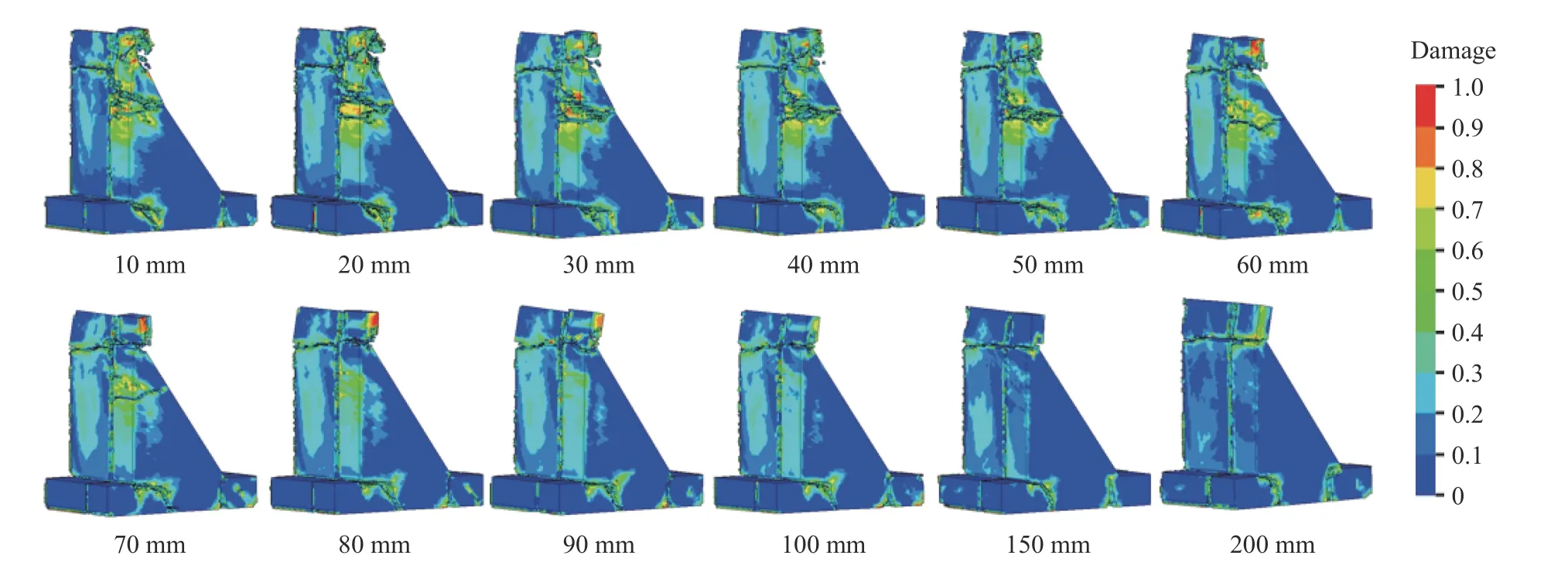
图6 爆深为50 mm 时不同爆距水下爆炸下重力坝的损伤Fig. 6 Damage clouds of dams due to underwater explosions at different standoff distances with the detonation depth of 50 mm

图7 爆深为100 mm 时不同爆距水下爆炸下重力坝的损伤Fig. 7 Damage clouds of dams due to underwater explosions at different standoff distances with the detonation depth of 100 mm

图8 150 mm 爆深不同爆距水下爆炸下重力坝的损伤Fig. 8 Damage clouds of dams due to underwater explosions at different standoff distances with the detonation depth of 150 mm

接下来将从上游坝面的损伤程度以及重力坝坝头、坝身和坝踵处的破坏描述爆距的影响。可以发现，相同爆深下，上游坝面损伤并非随着爆距增加而降低。以50 mm 爆深为例（图6），爆距从10 mm 增加到40 mm 的过程中，上游坝面损伤加剧，损伤面积逐渐增大，左边坝段尤为明显；爆距增加到60 mm 左右，上游坝面损伤才开始呈现下降趋势。爆深为100 mm（图7）和150 mm（图8）时，重力坝上游坝面损伤随爆距增加呈现类似的变化趋势。

进一步，从坝头处的破坏（图6）可以发现，爆距从10 mm 增加到200 mm 的过程中，坝头变截面位置均呈现整体水平断裂，这表明坝头是重力坝薄弱位置，容易遭到破坏。此外，当爆距较小时，上游坝面由冲击波入射形成的压缩应力波强度高，使得下游坝面反射形成的拉伸应力波同样具有较高强度，这导致小爆距时（爆距为10～40 mm），坝头下游坝面因拉伸应力波导致的剥落破坏严重；当爆距较大时（爆距超过80 mm），冲击波衰减严重，上游坝面压缩应力波强度降低使得下游坝面反射拉伸应力波强度较低，这使得爆距较大时坝头下游坝面几乎完好。

不同爆距水下爆炸冲击波荷载下，重力坝坝身处的破坏差别较大。爆深为50 mm（图6）、爆距为10～50 mm 时，坝身处破坏接近，均呈现为从上游坝面到下游坝面发展的倾斜贯穿断裂且断裂位置、宽度以及倾角基本相同。爆距增加到60～70 mm，在坝身相同位置仍呈现贯穿断裂，但该断裂宽度随着爆距增加降低且远小于爆距为10～50 mm 的结果。进一步，当爆距超过80 mm，随着冲击波荷载强度进一步降低，坝身处断裂消失。类似地，爆深为100 mm（图7）、爆距为10～40 mm 时，坝身处断裂相似；爆距为50～80 mm，坝身处断裂宽度显著降低且当爆距为80 mm，坝身处断裂未贯穿整个坝身；爆距超过90 mm，坝身处断裂消失。爆深为150 mm（图8）、爆距为10～40 mm 时，坝身处断裂相似；爆距为50 mm，坝身处断裂未贯穿整个坝身；爆距超过60 mm，坝身处断裂消失。

坝踵处的破坏呈现不同的变化规律。以50 mm 爆深为例（图6），爆距从10 mm 增加到40 mm，坝踵处破坏明显加剧表现为该处拉伸裂缝长度明显增长。爆距为50～90 mm，坝踵处裂缝长度没有明显变化且均比爆距为10 mm 的结果长。爆距超过90 mm 后，坝踵处破坏变得轻微，裂缝长度下降。从坝踵处的破坏随爆距变化规律可以发现，小爆距下，水下爆炸冲击波荷载对大坝整体弯矩更小导致坝踵处破坏更轻微，而适当增加爆距后，坝踵处破坏明显加剧。爆深为100 和150 mm，坝踵处破坏随爆距增加呈现类似变化趋势，不再赘述。

不同爆距水下爆炸冲击波荷载下重力坝的损伤破坏结果表明，水下爆炸对重力坝的毁伤效应并非随着爆距增加而下降。这是因为，尽管冲击波荷载强度随着爆距增加而下降，但冲击波荷载对重力坝产生整体弯矩使重力坝整体向下游弯曲并呈现整体弯曲导致的拉伸破坏。在这一破坏机制主导下，适当增加爆距，保证冲击波荷载强度较高的同时有利于冲击波荷载向重力坝坝顶和坝底传播。相比小爆距，适当增加爆距有利于增大冲击波荷载对重力坝的作用面积，从而对重力坝产生较大的整体弯矩并对重力坝产生更严重的毁伤。结合重力坝上游坝面损伤以及坝头、坝身和坝踵处的破坏，可以得到，50 mm 爆深时，30～50 mm 爆距附近，重力坝破坏最严重；100 mm 爆深时，40～50 mm 爆距附近，重力坝破坏最严重；150 mm 爆深时，30～40 mm 爆距附近，重力坝破坏最严重。上述结果和分析表明，水下爆炸对重力坝的毁伤效应不仅取决于冲击波荷载强度，同样依赖于重力坝的响应机理和破坏机制。对于重力坝整体结构破坏，如本文中重力坝整体弯曲导致的拉伸破坏，水下爆炸冲击波荷载对重力坝的毁伤效应存在“最优爆距”，在该爆距附近，重力坝破坏最严重。

2.2 损伤面积和平均损伤

为了佐证上述分析和结论并明确不同爆深下的“最优爆距”，需要进行更多的定量比较。从图6、图7 和图8 观察到，重力坝上游坝面损伤随着爆距增加呈现一定变化规律。表3 总结了各工况下，上游坝面损伤面积占上游坝面总面积的比值θ(L,R)以及上游坝面损伤区域各单元的平均损伤δ(L,R)。本文中，上游坝面损伤区域是指总损伤Dtot＞0 的区域，相应地，上游坝面损伤面积是指上游坝面损伤区域的面积。

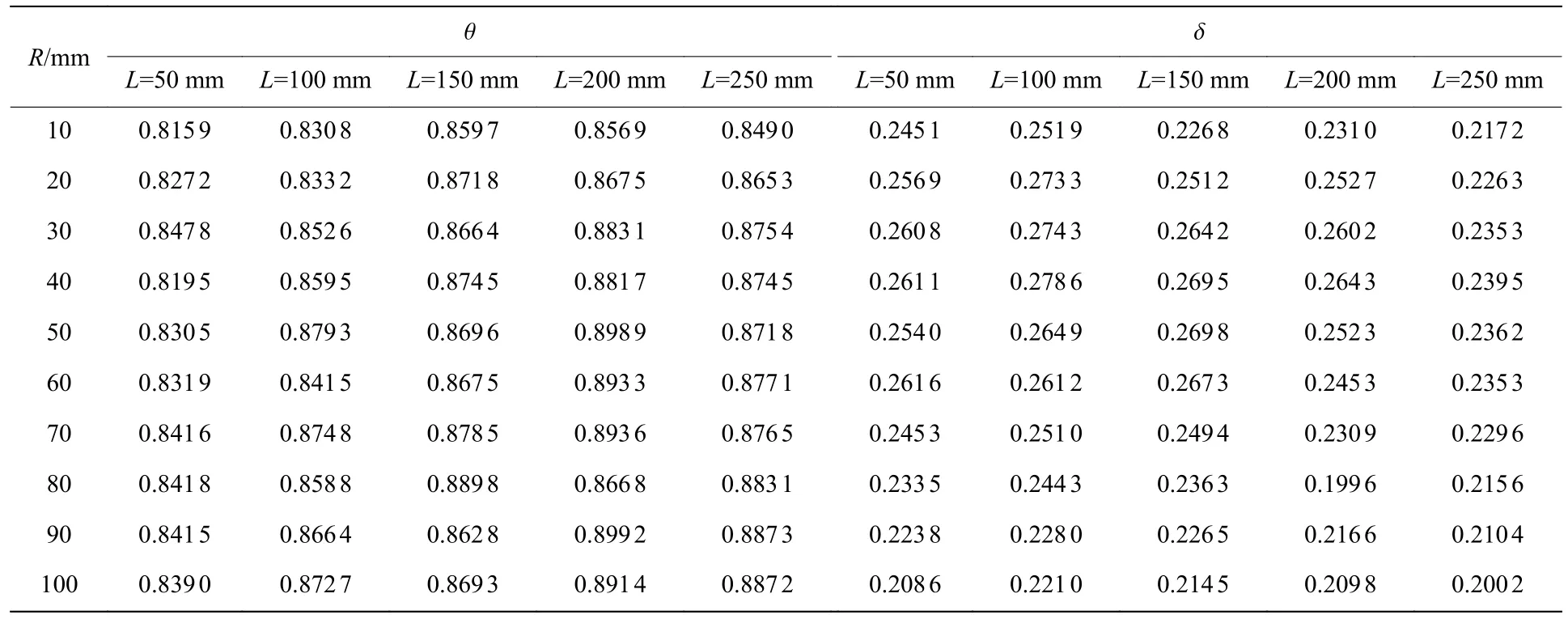
表3 上游坝面损伤面积占比θ 和损伤区域的平均损伤δTable 3 The damage area ratio θ and the average damage δ of the dam upstream face

为了表述方便，定义平均相对面积比参数ψR和平均相对损伤参数φR分别为

式中：R0=10 mm，为参考爆距。

图9 给出了ψR和φR与爆距R的关系曲线。可以发现：

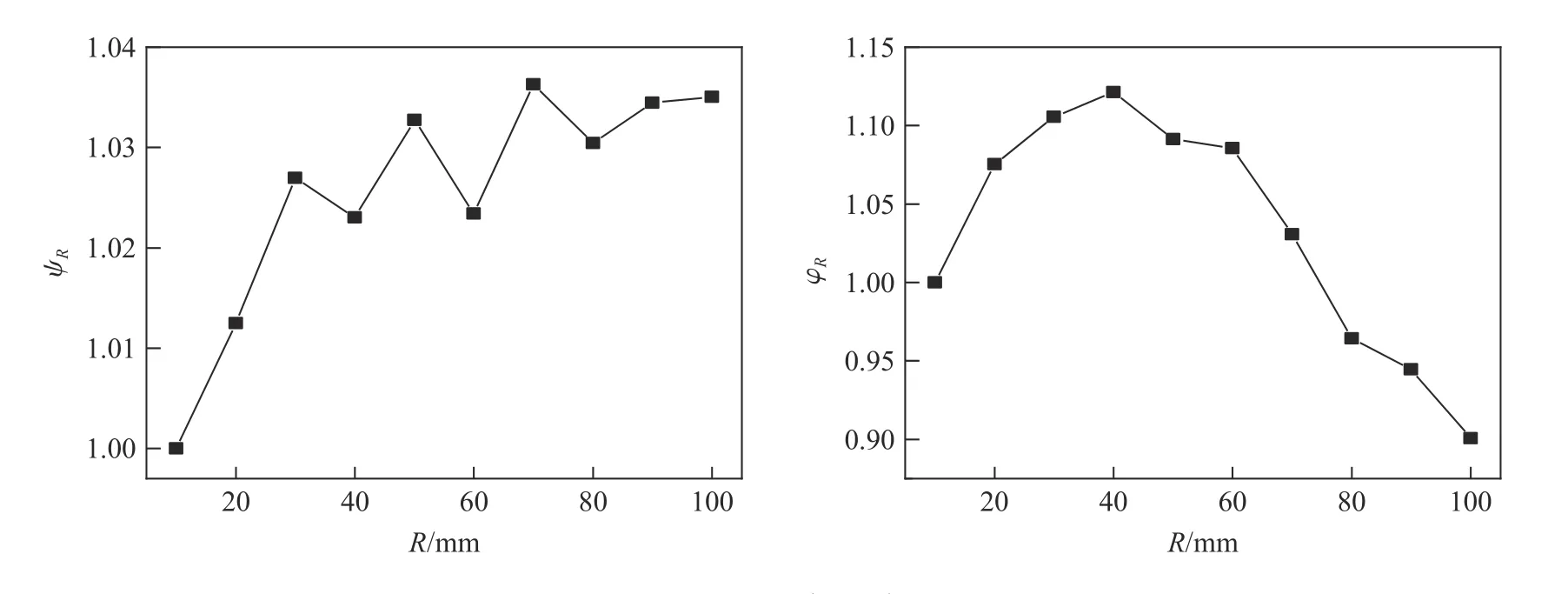
图9 ψR 和φR 与R 关系Fig. 9 parameters ψR and φR varies with standoff distance R

(1) 随着爆距增加，参数ψR均大于1 且呈现上升趋势，这表明，随着爆距增加，上游坝面损伤面积增大；这一结果佐证上述分析即小爆距时，水下爆炸冲击波荷载离坝面太近荷载过于集中，对大坝作用面积更小；而增加爆距，有利于水下爆炸冲击波荷载向整个上游坝面传播，从而对重力坝作用面积更大；

(2) 不同于参数ψR，参数φR随着爆距增加先增加后降低，爆距超过70 mm 后，参数φR小于1；这一结果表明，小爆距时，虽然冲击波荷载强度高但对重力坝作用面积较小，因而对重力坝的损伤破坏较小；大爆距时，尽管冲击波荷载对重力坝作用面积更大，但冲击波荷载强度衰减严重，因而对重力坝的损伤破坏同样较小；适当爆距下，冲击波荷载荷载强度较高同时对重力坝作用面积也较大，对重力坝的损伤破坏最严重，即水下爆炸对重力坝的毁伤效应存在“最优爆距”；5 组不同爆深的平均结果显示，40 mm 爆距为该模型配置（Hw=600 mm，W=2.2 g，n=80g）下的“最优爆距”。

应当指出，本文采纳的5 组爆深范围为50～250 mm，相比600 mm 水深，主要集中于近水面爆炸范围。在这一前提下，重力坝的损伤和破坏机制相近[29]，因此本文采用5 组爆深的平均值ψR和φR描述爆距的影响。

进一步，为了探究近水面水下爆炸时爆深对“最优爆距”的影响，图10 给出了L=50, 100, 150 以及200 mm 时，上游坝面损伤区域平均损伤δ 与爆距的关系曲线。可以发现，4 组不同爆深下，平均损伤δ 均在40 mm 爆距附近达到最大值，即“最优爆距”均在40 mm 附近，这表明，近水面水下爆炸时爆深对“最优爆距”不存在显著影响。后续需进一步探究深水爆炸时爆深对“最优爆距”的影响。

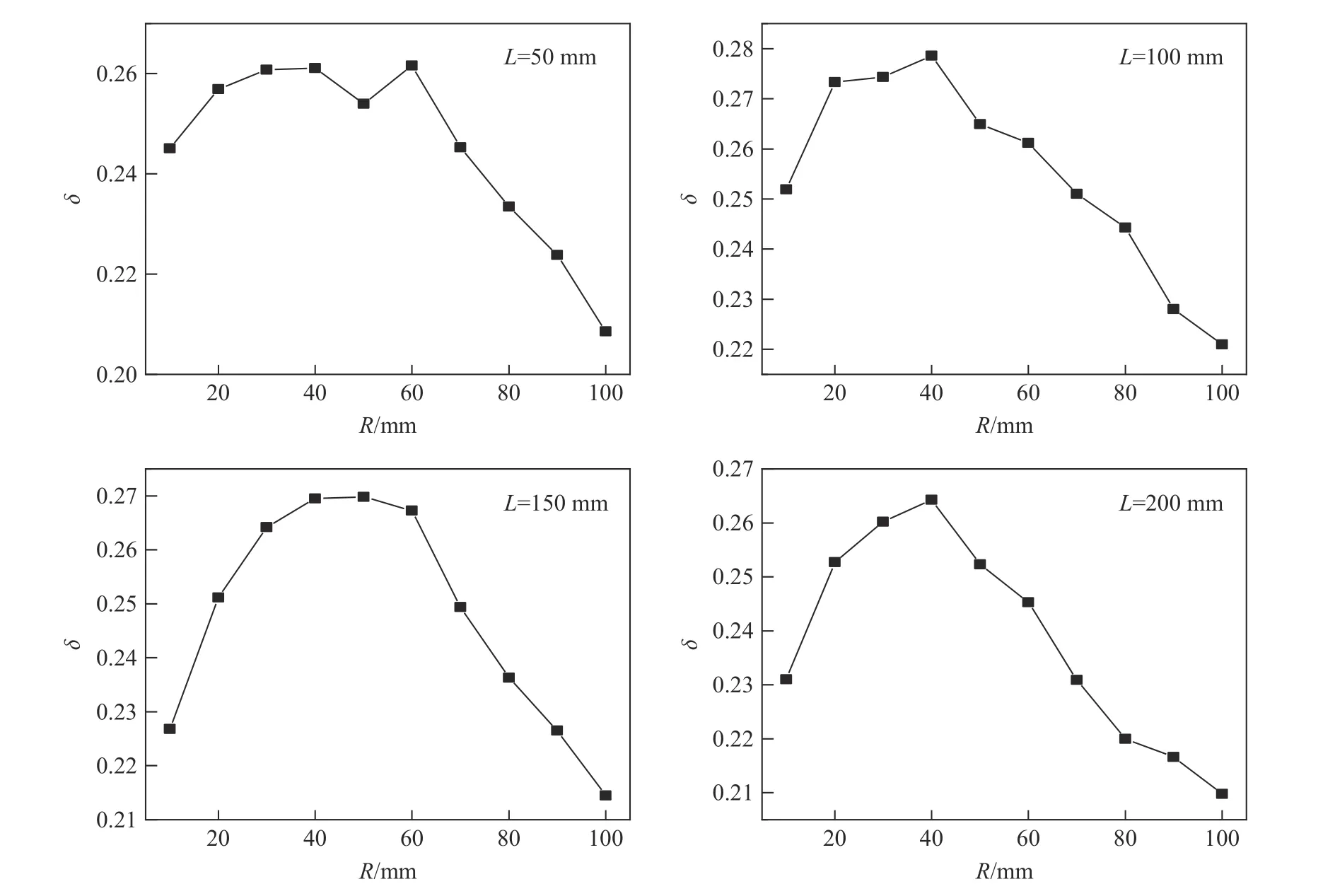
图10 平均损伤δ 与爆距R 的关系曲线Fig. 10 Average damage δ versus the standoff distance R

2.3 单元删除

从重力坝损伤破坏云图（图6、图7 和图8）可以发现，为了模拟重力坝的破坏如裂缝的萌发和发展，本文引入了单元删除准则。1.2 节介绍到，为了模拟拉伸破坏本文采纳了与拉伸损伤有关的单元删除准则，即当等效拉伸应变λt（见式(10)）超过用户定义临界值后，单元失效并被删除。用单元删除模拟重力坝的破坏，删除单元占总单元的比例即单元删除率，可反映重力坝的破坏程度。以50 mm 爆深为例，图11给出了不同爆距水下爆炸冲击波荷载下重力坝的破坏情形，并高亮标注了已删除的单元。可以发现，与图6 中坝头变截面位置的水平断裂相对应，该处删除单元沿着变截面位置水平分布。坝身断裂处删除单元也较为集中。可以发现爆距为40 mm，坝身断裂处删除单元密集说明该处断裂宽度较大，而爆距超过50 mm 后，坝身断裂处删除单元稀疏，表明该处断裂宽度显著降低。类似地，坝踵处删除单元的分布表明爆距从10 mm 增加到40 mm，坝踵处裂缝长度增长，破坏加剧；爆距为40～60 mm，坝踵处裂缝长度接近，破坏相似；爆距超过60 mm 后，坝踵处裂缝长度下降，破坏减弱。进一步，图12 定量给出了50 和100 mm 爆深水下爆炸冲击波荷载下重力坝的单元删除率与爆距的关系。可以发现，两组爆深下，随着爆距增加，重力坝单元删除率先增加后降低且在40 mm 爆距附近达到最大值。与重力坝损伤结果类似，从单元删除角度也能得到水下爆炸冲击波荷载对重力坝毁伤效应存在“最优爆距”且预测的“最优爆距”与基于损伤预测的结果接近。

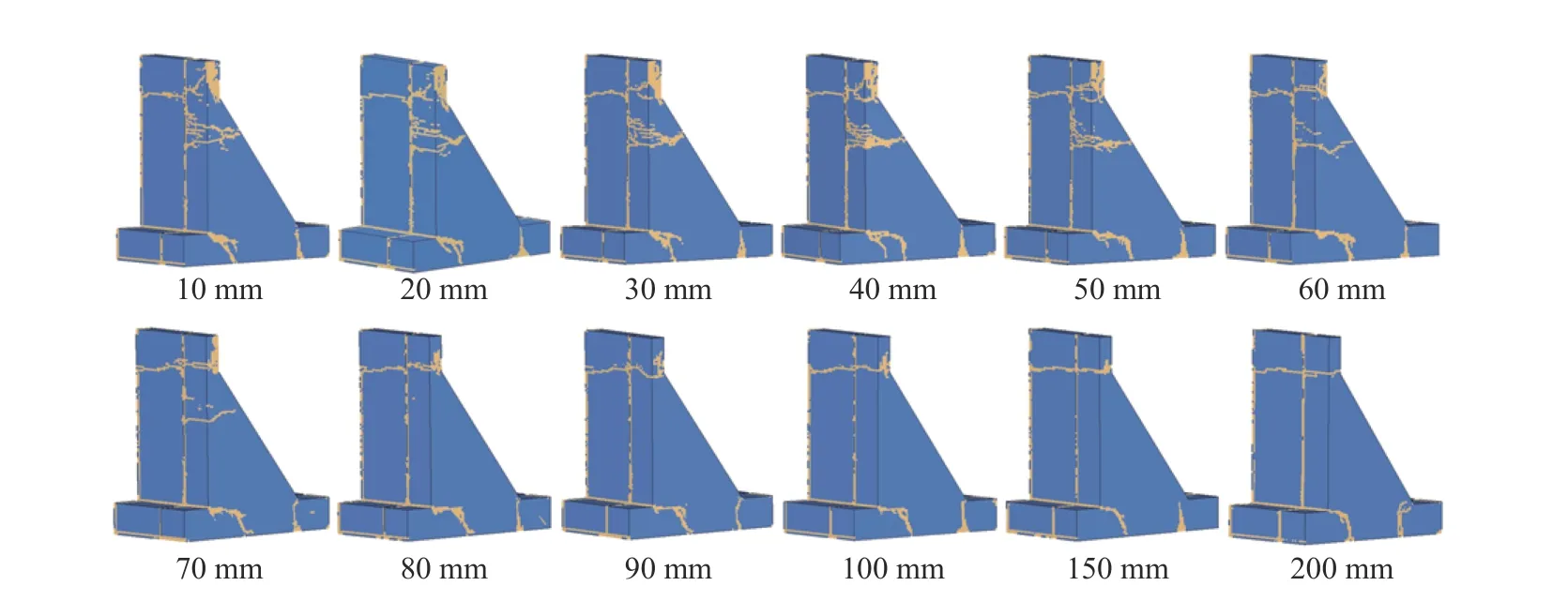
图11 50 mm 爆深不同爆距水下爆炸下重力坝破坏图（显示侵蚀单元）Fig. 11 Failure patterns of dams due to underwater explosions under different standoff distances with detonation depth of 50 mm (eroded elements shown)

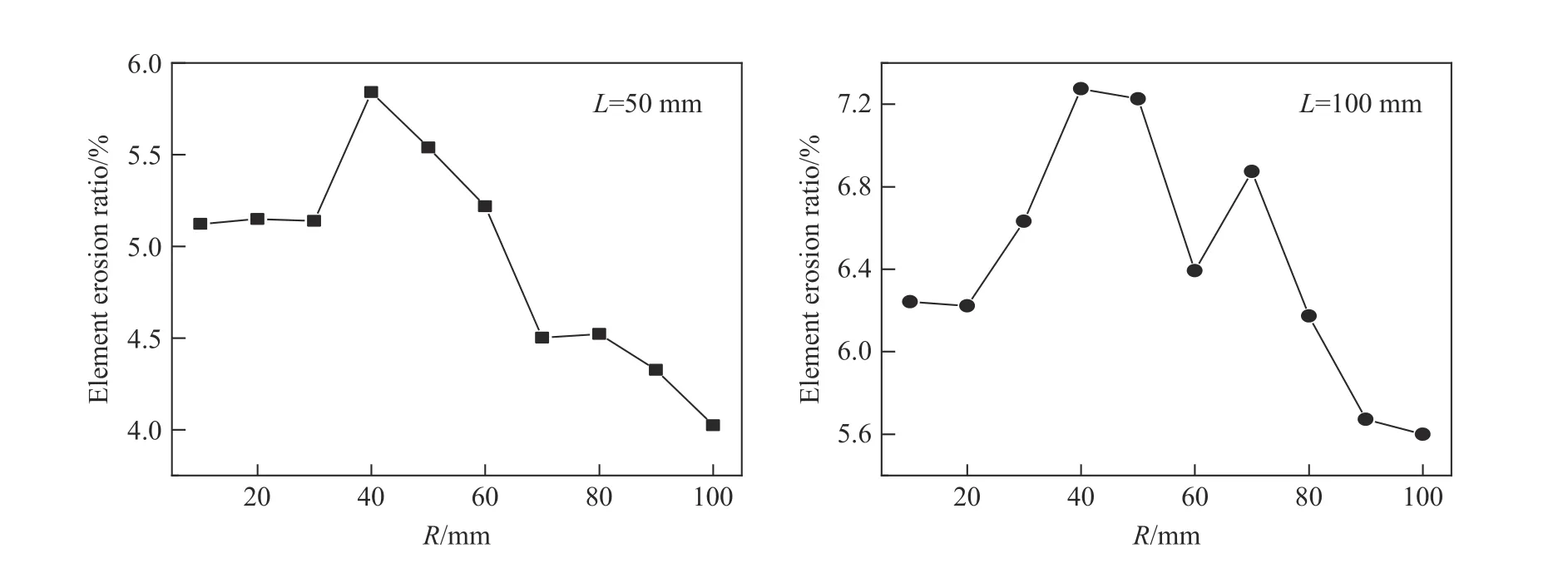
图12 重力坝单元删除率与爆距R 的关系曲线Fig. 12 The element erosion rate of the gravity dam versus the standoff distance R

2.4 应力和应变

除了重力坝的损伤破坏外，也可以通过对比重力坝应力、应变等参数佐证“最优爆距”的存在。已有研究[6-8]指出重力坝上游坝面的拉伸损伤以及坝头、坝身和坝踵处的破坏由重力坝整体弯曲导致的拉伸破坏机制主导，并指出重力坝三处主要破坏区域的应力、应变存在峰值。图13 给出了爆深为50 mm，爆距为20 和50 mm ，中间坝段上游坝面沿对称轴线（图1 中的线1）坝高方向的最大z向应力曲线。结合图1 和图6 可以发现，相应于坝头变截面位置、坝身断裂位置和坝踵位置的三处破坏，沿坝高方向的最大z向应力曲线存在三处对应的峰值。对于爆距为20 和50 mm 两种情形（图13），坝身断裂位置附近（z≈0.3 m）的最大z向应力峰值较为接近。相应地，两组爆距下重力坝坝身处断裂位置也较为相似（图6）。此外，图6 结果表明50 mm 爆距时重力坝坝踵处破坏比20 mm 爆距时严重，可以发现，爆距为50 mm 时坝踵处的最大z向应力比爆距为20 mm 时大。基于此，图14 给出了50 mm 爆深水下爆炸冲击波荷载下重力坝坝踵z方向的最大应力的平均值与爆距的关系曲线。可以发现，随着爆距增加，坝踵最大z向应力先增加后降低，峰值大致在40～60 mm 范围内。

图13 中间坝对称轴的最大z 向应力Fig. 13 The maximum z-stress curve along the axis of the middle dam

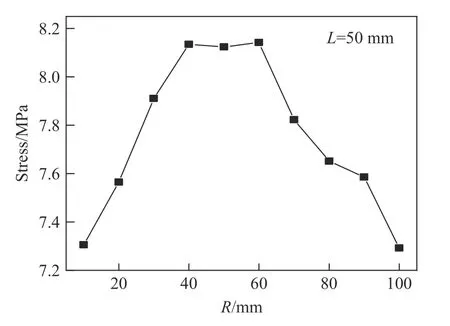
图14 中间坝对称轴坝踵处最大z 向应力的平均值与爆距R 的关系Fig. 14 Average of the maximum z-stress at the heel of the axis of the middle dam versus the standoff distance R

类似地，图15 给出了爆深为100 mm、爆距为10 mm 和50 mm 的情形下，左边坝段沿对称轴线（图1 中的线2）的最大z向应变。左边坝段仅坝头和坝踵处破坏明显，相应地，最大应变曲线在坝头和坝踵位置出现两个应变峰值。可以发现，爆距为50 mm 时两处应变峰值均比爆距为10 mm 的结果大。此外，图16 给出了爆深为100 mm 时重力坝左边坝段坝踵z方向最大应变的平均值与爆距的关系曲线。可以发现，随着爆距增加，坝踵z方向的最大应变先增加后降低且在50 mm 爆距时达到最大值。图13、图14、图15和图16 的结果表明，从重力坝应力、应变角度分析，同样可以得到水下爆炸冲击波荷载对重力坝的毁伤效应存在“最优爆距”且预测的“最优爆距”与通过重力坝损伤和破坏预测的结果接近。

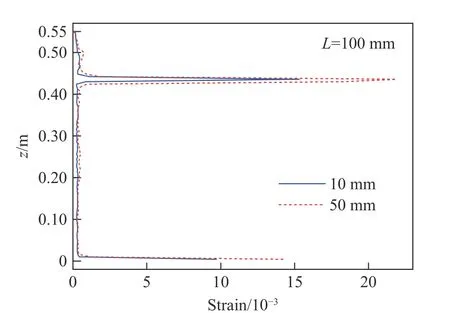
图15 左边坝对称轴的最大z 向应变Fig. 15 Maximum z-strain curve along the axis of the left dam

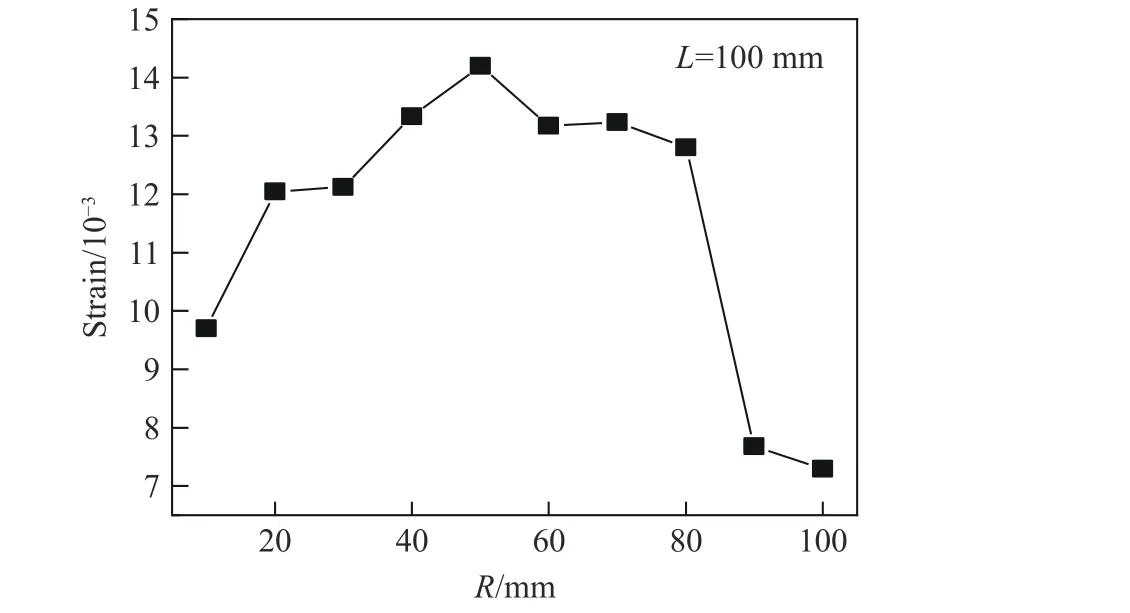
图16 左边坝对称轴坝踵最大z 方向最大应变的平均值与爆距R 的关系Fig. 16 Average of the maximum z-strain at the heel of the axis of the left dam versus the standoff distance R

3 结 论

基于前期开展的离心模型试验，本文通过建立炸药-库水-空气-重力坝结构的全耦合数值模型，对比分析了不同爆距水下爆炸冲击波荷载对混凝土重力坝的毁伤效应。为了说明水下爆炸对重力坝的毁伤效应存在“最优爆距”，设计了5 种爆深、每种爆深对应12 种不同爆距，共60 组数值计算工况。对比分析了相同爆深不同爆距水下爆炸对重力坝的毁伤程度并定量比较了重力坝上游坝面损伤面积占比、上游坝面损伤区域的平均损伤、重力坝单元删除率、坝踵最大拉应力的平均值、坝踵最大拉应变的平均值等参数。本文的主要结论如下。

(1) 水下爆炸冲击波荷载下，重力坝的毁伤程度不仅取决于水下爆炸荷载强度，同样依赖于重力坝的响应机理和破坏机制。对于重力坝整体结构破坏，如重力坝整体弯曲导致的拉伸破坏，水下爆炸对重力坝的毁伤效应存在“最优爆距”即随着爆距增加，重力坝毁伤程度先增加后降低。

(2) 随着爆距增加，重力坝上游坝面损伤面积增大，表明增加爆距，水下爆炸冲击波荷载对重力坝作用面积更广。

(3) 随着爆距增加，重力坝上游坝面损伤区域的平均损伤、重力坝单元删除率、坝踵最大拉应力平均值以及坝踵最大拉应变平均值均先增加后降低且都在40 mm 爆距附近达到最大值。

(4) 相同水深、炸药量和重力坝几何模型下，5 组不同爆深近水面水下爆炸对重力坝毁伤效应的“最优爆距”均在40 mm 附近，表明近水面水下爆炸时爆深对“最优爆距”不存在显著影响。

当水深、炸药量和重力坝模型相同时，“最优爆距”取决于两方面因素。一方面，冲击波荷载强度随着爆距增加而迅速衰减，因此，就冲击波荷载强度而言，小爆距时冲击波的毁伤效应更显著。另一方面，对于重力坝整体结构破坏，如本文关注的重力坝整体弯曲导致的拉伸破坏，增加爆距有利于增大冲击波荷载的作用面积从而对重力坝形成更大的整体弯矩。因此，就重力坝整体弯矩而言，大爆距时冲击波的毁伤效应更显著。在这两方面因素作用下，必然存在“最优爆距”，在该爆距下冲击波荷载强度较大同时对重力坝整体弯矩也较大从而对重力坝的毁伤效应最显著。对于本文采用的重力坝模型，在水深为600 mm、炸药量为2.2 g 的近水面水下爆炸的情形下，“最优爆距”在40 mm 附近。

应当指出，本文仅关注了冲击波的破坏效应，探讨了冲击波荷载下重力坝的破坏是否存在“最优爆距”。本文没有考虑气泡脉动、射流以及空化效应的影响，后续应当进一步探讨这些因素对“最优爆距”的影响以及炸药量、爆深等因素与“最优爆距”的关系。

此外，应当明确，本文采用小比尺模型进行计算和分析，得到的结果适用于小比尺重力坝模型。要将小比尺模型结果推广应用到原型重力坝，依赖于水下爆炸荷载下重力坝破坏的相似律，这需要后续进一步的研究。