基于相位重构的LFM信号间歇采样干扰产生方法研究

黄金刚，张夫龙，高 祺，刘 俊

（1.中国航天科工集团8511研究所，江苏 南京 210007；2.石家庄职业技术学院，河北 石家庄 050073）

0 引言

近年来，间歇采样已成为电子对抗领域的常用时域调制方法之一［1-2］，以间歇采样为基础产生了多种具体的干扰样式。

对于线性调频（LFM）信号，若只进行间歇采样调制，不叠加其他干扰调制，脉压后会产生主假目标和分布于主假目标前后的次假目标［3］。主假目标位置取决于间歇采样延时，用于自卫对抗时，位于保护目标之后，在带宽较小时，一侧的次假目标位于保护目标之前，但线调斜率较大时，仍旧落后于被保护目标。为解决此问题，常用的方法是对干扰信号进行移频处理［4］，该方法需要对雷达线性调频信号的带宽或线性调频斜率进行测量。

本文提出一种新方法，可以对间歇采样信号进行重构以消除转发延迟影响，从而实现干扰信号主峰与被保护目标重合。

1 间歇采样转发原理

常规间歇采样转发采用DRFM体制，接收一段脉冲后随即进行转发，然后再接收一段脉冲进行转发，如此重复形成间歇采样转发，分时处理过程如图1所示。

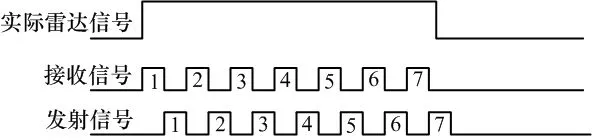
图1 间歇采样示意图

假设线性调频信号为：

式中，T为脉冲宽度，k为信号调频斜率，k=B/T，B为信号带宽。

对x(t)进行间歇采样，间歇采样周期为Ts，间歇采样频率为fs，得到信号xs(t)，其频谱为：

式中，an=τfsSa(nπσfs)为傅里叶级数系数，分量信号xsn(t)通过匹配滤波器后的输出为：

式中，τ为间歇采样周期内接收时的采样时间，对于占空比为1/2 时，其等于间歇周期内的干扰发射时间，τd为雷达回波固定路径延时，在不影响结果的情况下，可令τd=0。

xs(t)经过匹配滤波器后的输出为：

n的取值范围为-Np≤n≤Np，其中Np=B/fs。ysn(t)在t=t-nfs/k时刻达到峰值点，峰值为k(BT)1/2(1-|n|fs/B)。其中0阶信号始终滞后于目标回波信号时间τ，高阶假目标（主要考虑±1阶假目标）位置主要由间歇采样频率fs及调频斜率k决定。

可见，在一定的间歇采样频率fs下，LFM 信号调频斜率k越大，±1 阶假目标相对主假目标距离越小。在一定条件下无法将干扰能量置于保护目标之前。间歇采样脉压输出结果如图2所示。

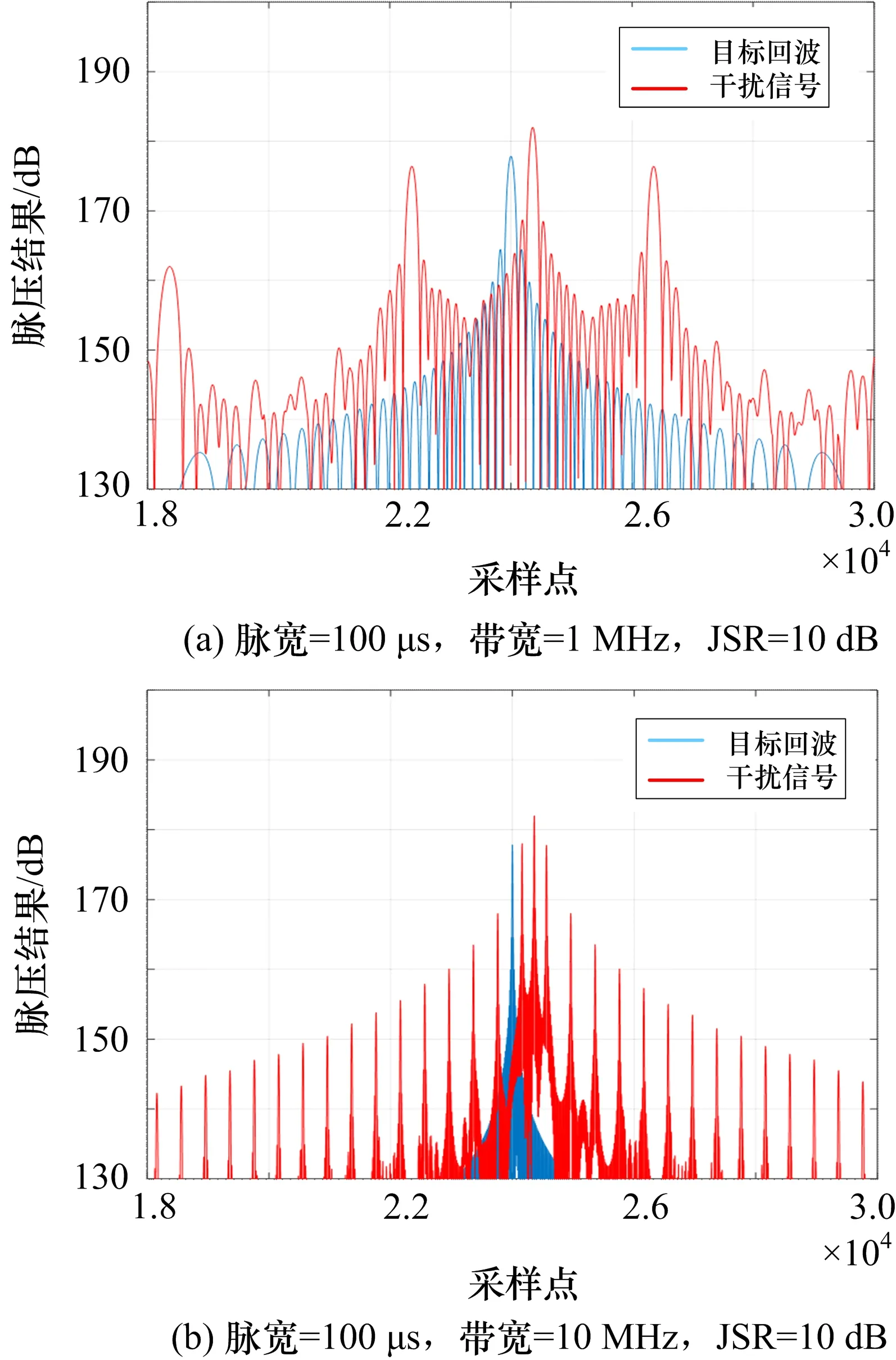
图2 间歇采样脉压输出结果

若通过信号重构可以将主峰相对于回波的延迟被消除，使干扰主峰与目标回波重合，再结合其他调制，便可将能量分布在回波前后两边，可有效应对各种CFAR检测方法。

2 相位重构信号原理

将信号x(t)分为M段时长为Δt的线性调频信号段SLFMi，对应的频率变化为[f，f+ Δf]，其中f为起始频率，Δf=kΔt。则线性调频信号段SLFMi可表示为：

取M段同样时长Δt的点频信号Si，每段点频信号Si与对应的线性调频信号段SLFMi的初始相位保持一致，载频为线性调频信号段SLFMi的中心频率，即fi=fLFMi0+Δf/2，其中fLFMi0是线性调频信号段SLFMi的起始频率。则点频信号Si可表示为：

取Hi(t)=S*LFMi(-t)，则线性调频信号段SLFMi经过匹配滤波器后的表达式为：

线性调频信号表达式为：

点频信号Si经过匹配滤波后的表达式为：

令t=0，则：

观察GLFMi(0)和Gi(0)的表达式可以发现，线性调频信号段SLFMi经过匹配滤波后幅度及相位完全相同，符合相参累积条件，能够获取M倍的积累增益；点频信号Si经过匹配滤波后幅度及相位也完全相同，同样能够获取M倍的积累增益。

对比GLFMi(0)和Gi(0)的表达式可以发现，相对于线性调频信号段SLFMi，每段点频信号Si经过匹配滤波器后，与其幅度之比为：

假设 Δt=n/n-1/2，n>0，则：

当n→0时，也就是如果点频信号拟合步进无限小，Gi(t)与GLFMi(t)将完全相同，这是因为把x(t)按时刻划分，x(t)就是由无数个频率线性变化的点频信号组成的。

当n逐渐增大时通过求和法近似计算出该定积分对n取不同值时带来的拟合损失，拟合曲线如图3所示。可以看出，当n≤1时，ratio>0.972 9，其损失可以忽略。

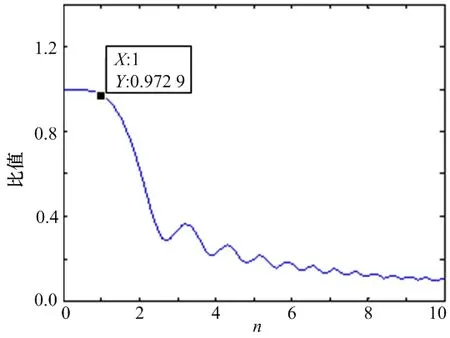
图3 脉压幅度随n值变化图

综上所述，取Δt≤k-1/2，用线性调频信号每段的中心频点对该线性调频信号进行拟合。

采样量化信号与相位信息一一对应，对于恒幅信号，只要获取每个时刻的相位信息，便可还原量化信号。

假设某段线性调频信号对应的相位可表示为：

单载频信号频率为该段中心频率可以利用结束相位和初始相位计算：

因此，只需要获取分段脉冲结束相位信息与初始相位信息，便可使用单载频拟合线性调频，最终完成信号的重构，此处的相位为无模糊相位，即与初始相位差不存在周期性2π模糊。

对间歇采样，若可以通过采样段相位得到发射段相位，便可重构无延迟发射信号。

3 间歇采样线性调频信号重构

线性调频信号信号对应的相位可表示为：

间歇采样某段收发时间原始信号信息如图4所示。

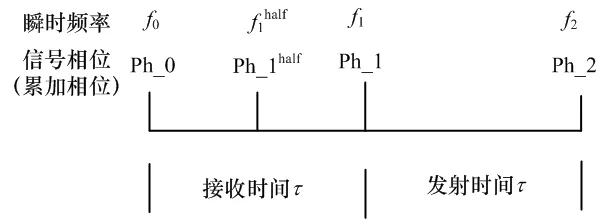
图4 接收时间和发射时间对应相位频率示意图

图4中 ph_1half，ph_1，ph_2相对于 ph_0均为无 2π模糊相位，存在以下对应关系：

将f1=f0+kτ代入得到如下信息：

在接收时间窗一半的位置，有如下的对应关系：

结合 ph_1-ph_0=2π(f0τ+kτ2/2)可得：

将 (ph_2-ph_1)-(ph_1-ph_0)=2πkτ2代 入式（20）可得：

发射周期内的短时线性调频信号，使用单载频线性拟合表达为：

则得到：

由此，可以通过接收信号的相位得到发射时间拟合的原始信号相位，采用了短时单载频拟合短时线性调频，拟合后的初始相位和结束相位与原始信号相同。

4 仿真试验

设步进频雷达信号脉宽T=90 μs，带宽B=1 MHz，干扰机间歇采样时长 3 μs，间歇周期为 6 μs，仿真中频采样率为100 MHz，干信比设置为10 dB。重构信号主峰与回波信号位置一致。脉压仿真结果如图5所示，归一化目标回波波形与重构波形如图6所示，波形局部放大图如图7所示。

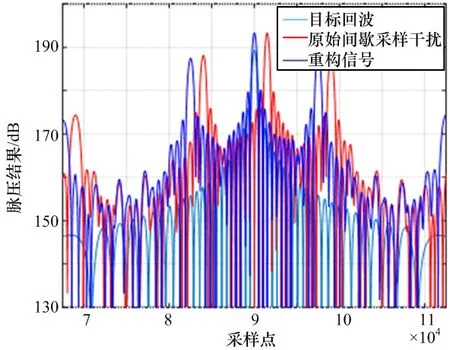
图5 脉压仿真结果

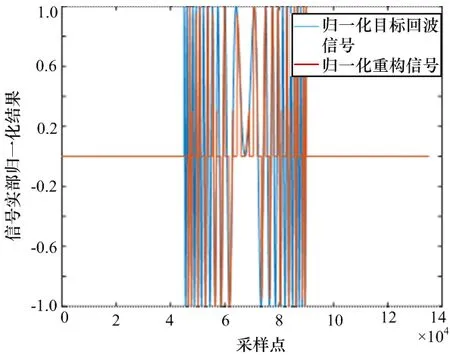
图6 归一化目标回波波形与重构波形

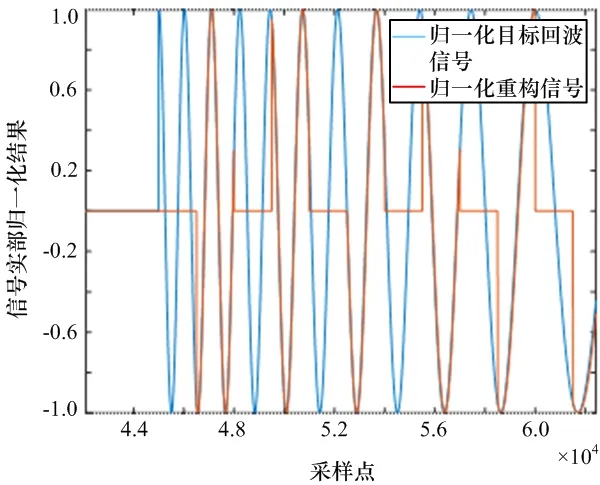
图7 波形局部放大图

将带宽B变更为10 MHz，可知重构信号主峰与回波信号一致。从信号的局部放大图可以看出每一个间歇复原信号与回波信号的起始和终止信号完全一致，每段使用不同的单载频信号进行拟合，实现了较好的信号复原，抵消了间歇采样带来的时间延迟。脉压仿真结果如图8所示，归一化目标回波波形与重构波形如图9所示，波形局部放大图如图10所示。

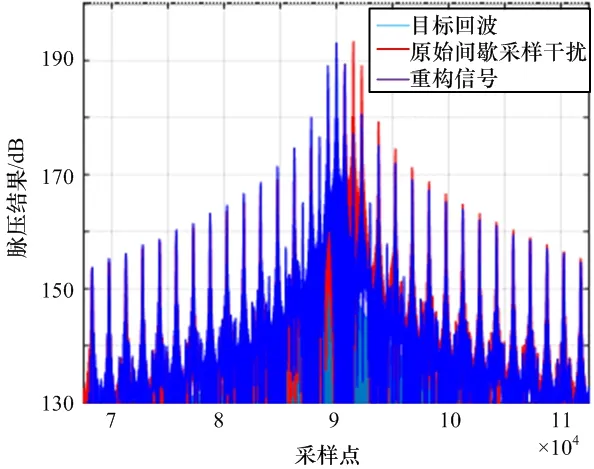
图8 脉压仿真结果

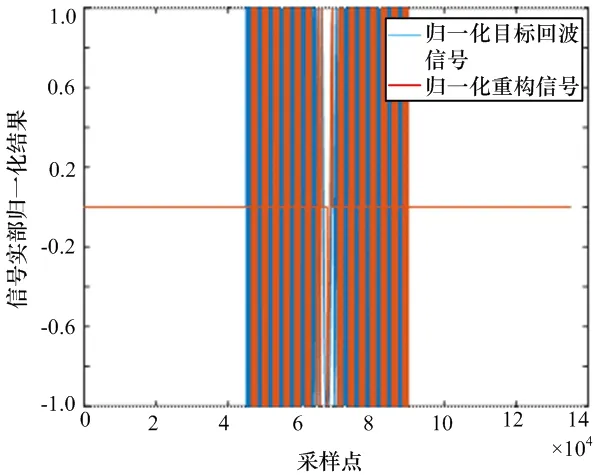
图9 归一化目标回波波形与重构波形

图10 波形局部放大图

5 结束语

本文提出了一种全新的信号重构方法，并未对信号斜率进行直接的精确测量，而是使用相位信息，采用分段短时单载频拟合分段短时线性调频，分段处理亦不存在累计误差。从脉压效果看，该拟合保持了信号的相参特性。仿真结果表明该方法重构效果理想，具有良好的工程应用价值。