前斜视SAR成像中几何校正问题研究

刘业民，刘晓娴，袁 露，曾广论，吕汉峰

（1.中国人民解放军第32579部队，广西 桂林 541001；2.中国人民解放军第93209部队，北京 100085）

0 引言

合成孔径雷达（SAR）具有全天时、全天候的观测能力，且在一定波段条件下可穿透云雾的遮挡，因此，SAR被广泛应用于军事、民用等领域［1］。SAR成像技术是SAR技术的重要组成部分，为了实现实时情报侦察、火力引导、察打一体和热点地区重访，军用SAR体制成像时通常采用前视或前斜视工作模式［2-4］。由于斜视角、非理想飞行轨迹等因素，SAR图像目标的位置会发生偏移、旋转、影像失真等情况，通常需要进行几何校正［5］，为后续目标识别和定位提供基础。因此，研究SAR图像的几何校正贴近现实需求，具有重要的军事意义。

关于SAR图像的几何校正大致可分为2类：第一类是与SAR成像算法本身无关的几何校正，例如，校正SAR影像固有的透视收缩、叠掩和阴影等几何失真［6］，校正因SAR载机平台非理想运动而造成的图像失真［7］等等；第二类是与成像算法本身有关的几何校正，当成像目标与SAR载机平台存在一定角度时，SAR图像目标的位置一般会发生偏移和旋转，需要在成像算法中进行几何校正。本文研究的是第二类几何校正问题。文献［8-11］研究了俯冲弹道下SAR成像的几何校正方法；文献［12］研究了聚束SAR快速分级后投影算法下的几何校正问题；文献［13］研究了前斜视SAR成像几何形变校正方法，然而该文献只研究了目标位置偏移几何校正方法，SAR图像旋转校正方法在文中并未给出。通过研究文献［14］给出的chirp变标（CS）算法，可以发现该书中关于成像目标的几何校正问题仍然有2点需要进一步完善：一是书中未给出目标成像后距离向和方位向位置校正函数，按照给出的成像算法进行成像处理，其目标的成像坐标位置与原设定位置在距离向和方位向均存在位置偏差；二是由于前斜视成像点目标旁瓣与书中给定的零多普勒坐标系存在夹角，因而无法直接评估目标的成像品质，需要对成像目标做进一步的几何校正处理，但书中并未给出其具体的处理方法。关于如何解决上述的第二个问题，目前主要有2种思路。第一种思路是将图像聚焦在数据录取坐标系上，确保前斜视SAR成像后目标旁瓣与数据录取坐标系平行，文献［15］根据该思路提出一种将图像聚焦到任意给定坐标系的方法，然而该方法需要对目标图像作尺度傅里叶变换，且与常用的零多普勒坐标系不一致，通常还需要进一步做几何校正［5］。第二种思路是对目标图像作旋转处理，以消除与给定成像坐标系的夹角，该思路可操作性强，且便于实现，其本质是坐标系旋转和数据插值问题。本文采用的是第二种思路。基于上述背景和问题，本文对文献［14］中CS成像算法几何校正问题进行了研究，旨在进一步补充完善文献［14］中CS成像算法流程。

1 CS成像算法流程

图1给出了前斜视SAR成像的空间几何模型。x轴为方位向，R轴为距离向，θs为斜视角，SAR载机平台以速度为va沿x轴正方向直线匀速运动，雷达目标P为场景中心参考目标，与SAR载机平台最近距离为R0。设以平台位于A点的时刻为慢时间ta的起点，此时波束射线与通过P点且平行于x轴的线段相交于B。经过慢时间ta后，平台移动到A′，其横坐标为vata。设雷达目标P与B点的方位向距离为x。由图1的几何关系可知，从三角形ΔA′PB′可得到SAR载机平台到目标P的瞬时斜距R(ta)可表示为：

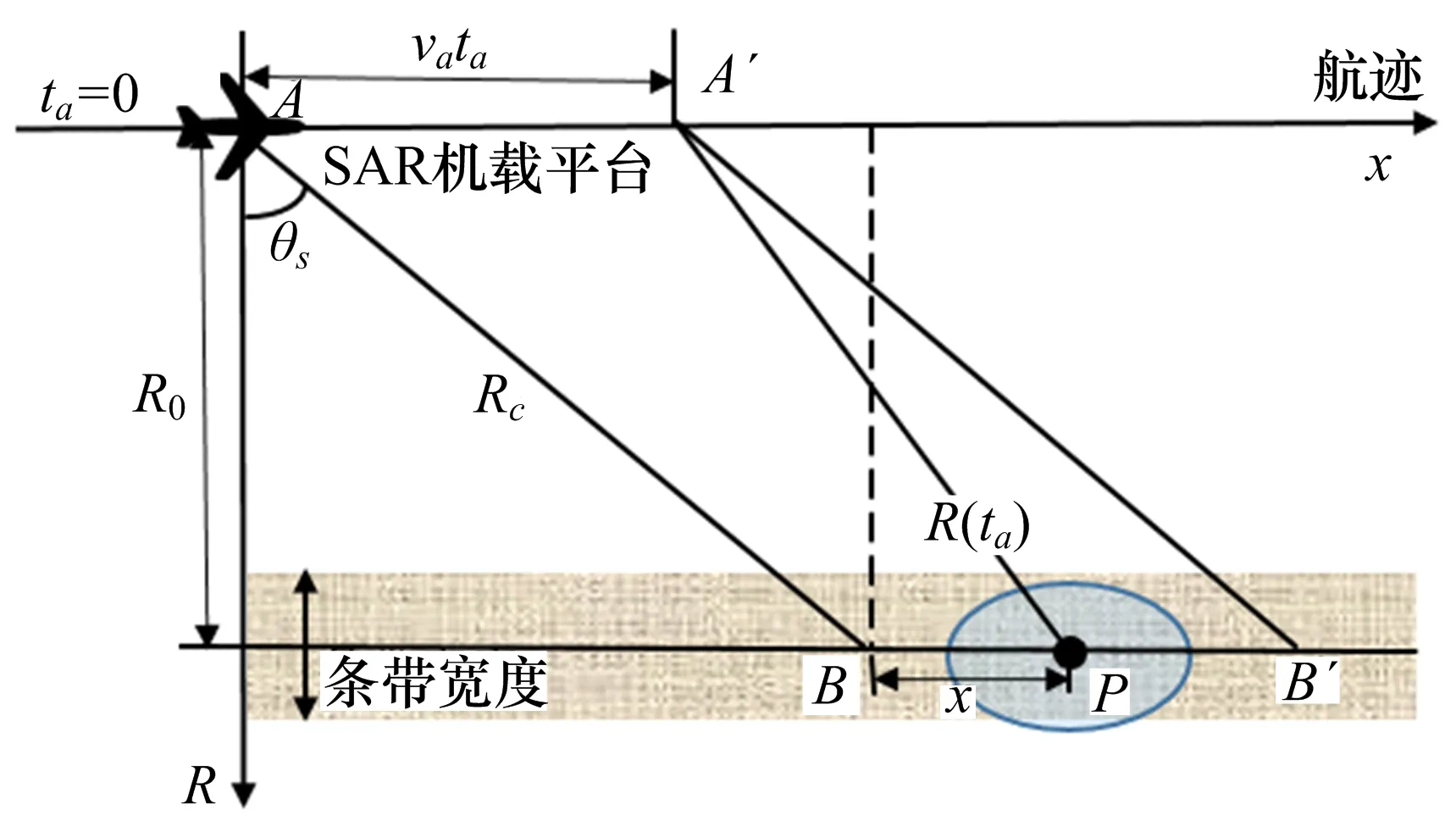
图1 前斜视SAR成像空间几何模型

式中，Rc=R0/cosθs。

假设SAR发射的信号为线性调频信号，其信号形式为：

式中，rect()⋅为矩形窗函数，Tp为发射信号脉宽，f0为信号载频，Kr为线性调频率，tr为距离向快时间，t为全时间，且t=tr+ta。

那么，SAR接收到目标P的基带回波信号可表示为［14］：

式中，σ为目标后向散射系数，c为光速，λ为信号波长；wr(·)和wa(·)分别为距离窗函数和方位窗函数。在式（3）中，第1个指数项表示波束扫过目标形成的多普勒历程，其与目标的方位压缩和二次距离压缩（SRC）有关；第2个指数项是发射信号的距离向延迟，涉及到目标的距离压缩。CS成像算法主要步骤包括［14］：距离走动校正、补余距离徙步校正（RCMC）中的Chirp Scaling操作、距离压缩、SRC、一致RCMC、方位压缩及相位校正、方位向校正以及图像旋转校正，其成像算法流程如图2所示，算法的具体细节，请参考文献［14］。虚线框部分为CS算法流程的几何校正步骤，也正是本文所需研究的问题。

图2 CS成像算法流程图

2 前斜视成像的几何坐标系

如图1所示，xOR坐标系为零多普勒坐标系［5］，当斜视角不为零时，成像目标的旁瓣与xOR坐标系存在夹角，其夹角大小等于斜视角θS；另一个坐标系为数据录入坐标系，记为x′OR′坐标系［5］，如图3所示，在该坐标系中得到的图像纵轴为雷达视线所指的斜距方向，横轴为与雷达视线正交的方向，它与零多普勒坐标系中的距离向和方位向均不一致。

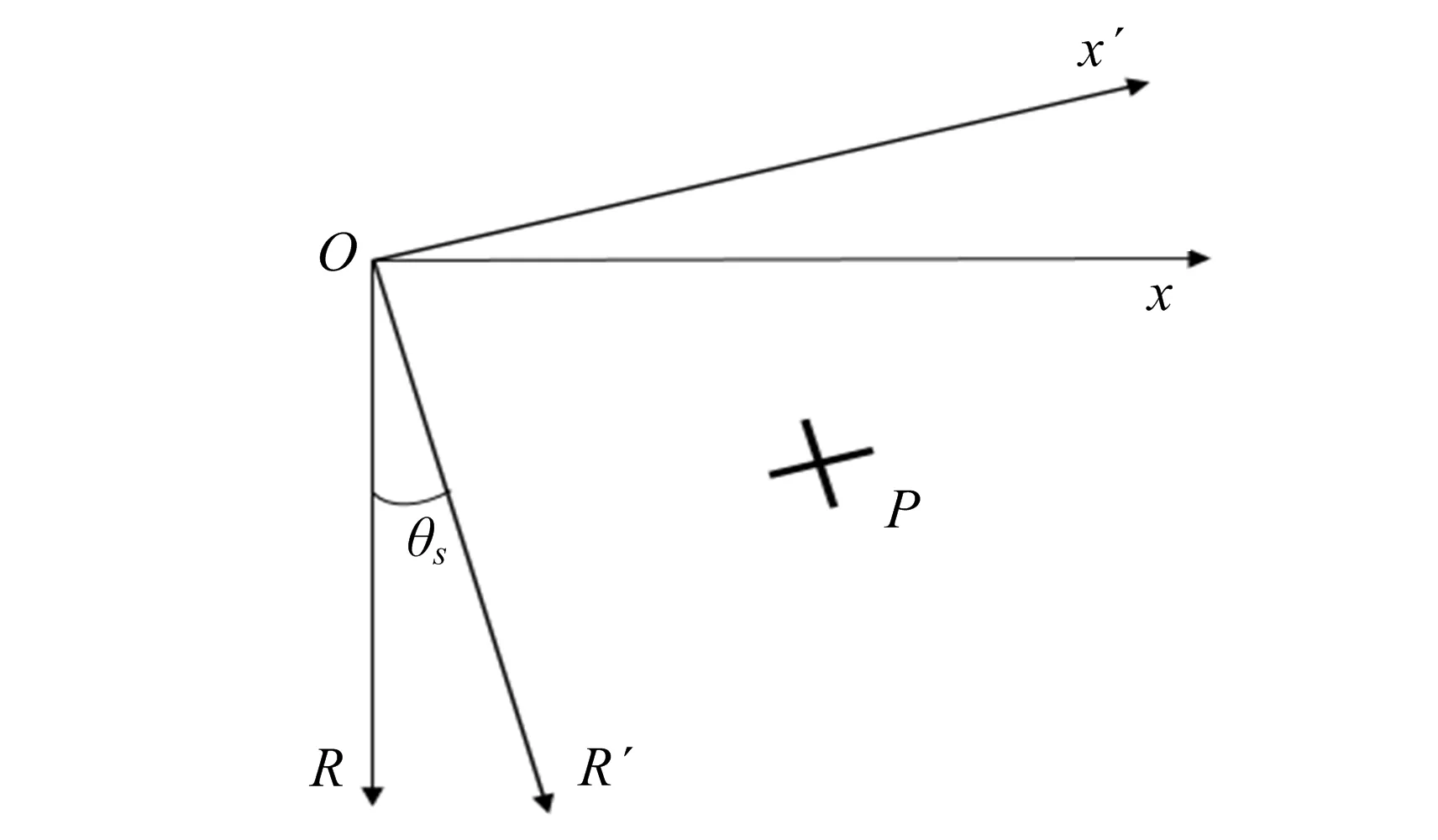
图3 点目标在不同坐标系成像示意图

在x′OR′坐标系中，点目标P的旁瓣（图中用“十”字符号表示其旁瓣）与坐标轴平行，在该坐标系下成像目标便于进行成像品质评估，但图像聚焦到x′OR′坐标系需要对图像作尺度傅里叶变换和几何校正［15］；在xOR坐标系中，点目标的旁瓣与坐标轴存在夹角，不便于直接进行成像品质评估，需先校正图像位置后再对图像作旋转处理，但无需对图像作尺度傅里叶变换，相对于在x′OR′坐标系中处理几何校正更为简单。因此，本文所提的几何校正方法在xOR坐标系中进行。

3 几何校正

在xOR坐标系中，对文献［14］中CS算法的几何校正分2步进行：第一步是校正成像目标距离向和方位向位置；第二步是对图像作旋转处理。其中第二步不是必须的，它主要用于对成像目标进行成像指标品质测试和评估。

首先研究成像目标距离向和方位向位置校正问题。对式（1）在x处按泰勒级数展开并保留到二阶项，有［2］：

式中，Rw(ta)=sinθsvata为距离走动项，当斜视角θs不为零时，距离走动对后续成像的影响不可忽视，会导致目标聚焦不理想和目标压缩后距离向位置不正确［2］，需进行距离走动校正。距离走动校正可以在频域上进行也可以在时域上进行，本文在时域上进行，即将距离走动校正函数HW与下变频目标回波相乘（对应于图2流程图中的第一个虚线框），HW的表达式为：

距离校正函数完成后，按照图2的算法流程，在方位压缩和相位校正后，其回波信号可表示为：

式中，A为复常数，fa为方位频率，fac为方位中心频率；pr(·)为距离向点扩展函数，Wa(·)为天线波束方位图的多普勒频谱包络，D为距离徙步因子［14］。式（6）中的指数项与目标方位向峰值位置有关，会引起方位向峰值位置偏移，因此需要对其进行校正（对应于图2流程图中的第二个虚线框），其方位向校正函数表达式为：

完成方位向位置校正后，再进行方位向IFFT，最终便得到了距离向和方位向校正后的目标二维成像结果。

下面研究成像目标旋转处理问题。成像目标作旋转处理的本质是对目标图像进行坐标系旋转和数据插值。以Matlab仿真软件为例，阐述成像目标旋转处理流程（对应于图2流程图中的第三个虚线框），其具体步骤共分为5步：

Step 1：确定目标距离向和方位向中心坐标位置和截取升采样点目标成像区域。在最终生成的升采样图中确定需作旋转处理点目标的距离向和方位向中心坐标位置，然后根据中心坐标位置截取合适的目标成像矩形区域。

Step 2：计算旋转后距离向和方位向采样间隔。若旋转前的距离向和方位向采样间隔分别为ΔR和ΔA，则旋转后的距离向和方位向采样间隔ΔR′和ΔA′的计算公式为：

Step 3：旋转坐标系并确定旋转后的坐标范围。若截取后的未旋转图像距离向和方位向的采样点分别为Nr和Na，则旋转前距离向和方位向的坐标可表示为：

式中，floor(·)表示向下取整操作符。根据坐标系旋转公式，旋转后的坐标系可表示为：

然后由R′和x′可分别确定距离向和方位向的坐标范围分别为R′max、R′min、A′max和A′min。

Step 4：计算旋转后的重采样距离向和方位向坐标。由R′max、R′min、A′max和A′min可确定旋转后坐标系距离向和方位向的采样点数分别为：

则旋转后重采样距离向和方位向坐标可分别表示为：

Step 5：数据网格化处理。使用Matlab软件中的内置函数griddata（）函数作数据网格化处理，数值插值选择线性插值即可。数据网格化处理完成后，使用式（12）中的重采样坐标系并考虑其目标的中心坐标位置即可正确显示出旋转后的目标图像。

4 仿真实验验证与结果分析

用仿真实验验证文中所提几何校正方法的可行性。在仿真实验中，假设SAR工作在条带模式，其系统仿真参数如表1所示。

表1 SAR系统仿真参数

在成像场景中设定5个静止目标，分别用P1—P5标识，相邻目标其距离向和方位向间距均为100 m，其位置分布示意如图4所示。图5给出了图像位置校前的目标成像图，图6给出了图像位置校后的目标成像图。对比图5和图6可以看出，若未对SAR图像进行位置几何校正，则其成像目标距离向和方位向位置会产生偏移，尤其是目标方位向的偏移量会比较明显。

图4 场景目标位置设定示意图

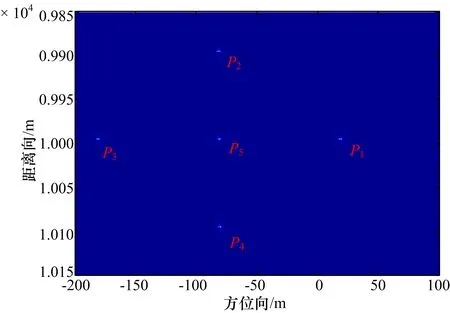
图5 校正前目标成像图

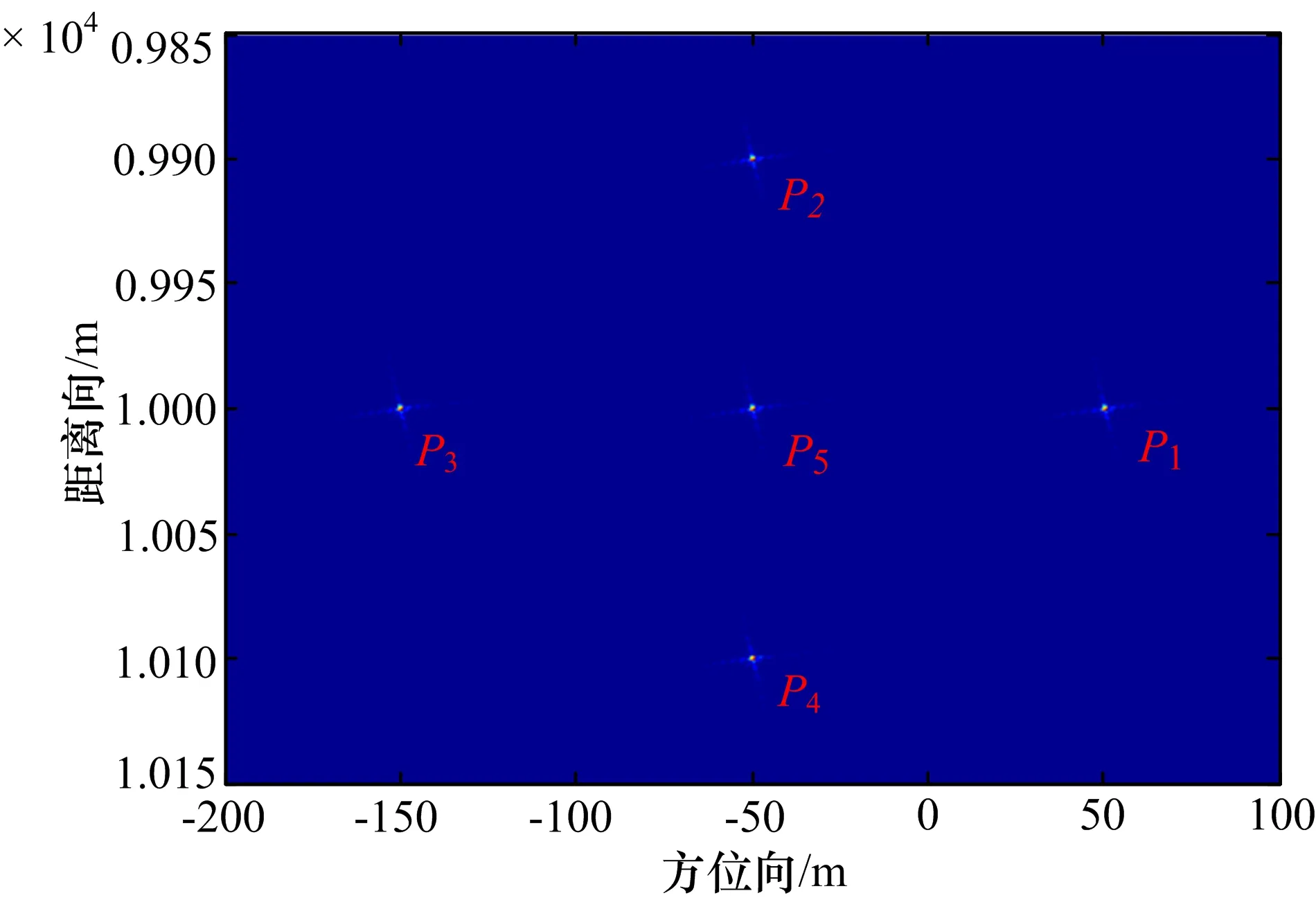
图6 校正后目标成像图

图7和图8分别给出了目标1、目标2以及目标5旋转前和旋转后的二维升采样成像图，图9给出了图8中目标距离向和方位向剖面图，为简洁直观，图7—9中纵坐标表示距离向坐标值时，均与中心场景斜距R0做了差值处理。为验证旋转后的图像是否适用于成像品质的评估，表2给出了目标P1—P5旋转后目标成像品质量化指标。量化指标主要包括目标峰值位置偏移误差、目标冲击响应宽度（IRW）、目标峰值旁瓣比（PSLR）以及目标积分旁瓣比（ISLR）。

图9 目标升采样剖面图

表2 目标成像品质指标

从图7—9以及表2中可以得出如下2个结论：1）对SAR图像经目标位置偏移几何校正后，其目标距离向和方位向峰值位置偏移误差很小，验证了位置几何校正效果良好；2）把表2中成像量化指标与文献［14］中量化指标数进行对比，发现两者的数值相当。因此，经旋转后的图像可用于斜视SAR目标成像品质的评估。综上可知，仿真实验验证了本文所提校正方法的可行性。

5 结束语

本文研究了前斜视SAR成像中的几何校正问题。以经典的CS成像算法为例，提出了一种SAR目标位置偏移几何校正方法，所提方法进一步补充完善了文献［14］中CS成像的算法流程。仿真实验表明，在斜视角为10°的情况下，经过位置偏移几何校正后，目标距离向和方位向峰值位置偏移量误差小于0.052 m；提出了一种用于评估目标成像品质的图像旋转校正方法，该方法通过坐标系旋转和数据插值即可实现SAR图像的旋转，且旋转后的图像不变形扭曲。文中所提的几何校正方法简单实用，可为其它前斜视SAR成像算法的几何校正提供借鉴和参考。