单位面积时频块上的噪声特性分析与信号检测

石 荣，宋庆军，胡 柱

（电子信息控制重点实验室，四川 成都 610036）

0 引言

在电磁信号的时频分析中单位面积的时频块意味着 Δf⋅Δt=1，其中 Δf为对应的频宽，单位 Hz，Δt为对应的时宽，单位s。尽管从理论上已经证明：任何信号均满足Δf⋅Δt≥12［1-2］，但从工程应用的角度讲，单位面积的时频块是时频面上可分辨的最小面积的时频块，这是由于工程上最常用的时频分析工具为短时傅里叶变换，变换之前的时域采样数据的时间分辨率最高，而变换之后的频域频谱数据的频率分辨率最高，但无论采用多长时间段的采样数据进行变换，在时频面上观察，仍旧保持了最小可分辨的时频单元格的面积为单位1的特性［3-4］。单位面积时频块上的噪声及信号特性实际上在工程应用中广泛涉及。在数字通信中一般以Eb/n0尺度下的误码率或Es/n0尺度下的误符号率来度量通信传输的性能，其中Eb和Es分别表示承载一个比特和一个符号的信息所需要的信号能量［5-6］。在匹配滤波的性能表征中通常使用Esig/n0来表示滤波处理所能获得的收益，其中Esig为目标信号的能量［7］。在干涉仪测向应用中同样使用Esig/n0来计算干涉仪通道间信号相位差测量所能达到的精度［8］。在以上性能评价中都使用了单位带宽内的噪声平均功率n0作为共同的尺度参考，n0的单位是WHz=J，实际上焦耳J是一个能量单位，这同时也说明：前述的Eb/n0、Es/n0和Esig/n0均是能量信噪比。其实n0也表示了单位面积时频块上的噪声平均能量，因为单位带宽即为1 Hz，信号功率对应了1 s时间长度内的信号能量，1Hz⋅1s=1，即单位1，这对应了单位面积的时频块，即Δf⋅Δt=1。

由上可见，在工程应用中单位面积时频块上的噪声特性备受关注，其所具有的平均能量n0也作为各种性能评价的共同参考尺度而广泛使用，但截至目前，对单位面积时频块上的噪声特性的分析与总结还不够全面与深刻。对此，本文在对单位面积时频块上的噪声分布及统计特性进行简要概述的基础上，对n0的测量与接收系统G/T值之间的关系，以及匹配滤波中信号相干积累与n0相关的能量信噪比的度量进行了详细分析，揭示了n0的本质物理意义。接着对单位面积时频块的各种划分方式，以及相关的信号检测应用进行了总结，最后提出了基于等比尺度分级划分的时频分析工程实现方法。

1 单位面积时频块上的噪声统计特性

实信号采样定理要求采样频率要大于信号最大带宽的2倍以上；而复信号采样定理仅要求复采样频率大于1倍信号最大带宽即可。由于复采样时I/Q双通道同时对复信号的实部与虚部进行采样，所以这等效于总的单通道采样频率增加了1倍，所以复信号采样定理与实信号采样定理本质上是等价的。在本文中为了表述方便，后续均采用复采样定理。

以工程上常见的加性白高斯噪声（AWGN）为例来阐释单位面积时频块上的噪声特性。设复采样率为fs，对带宽不超过fs的一段AWGN信号进行采样，得到Ns个时域采样点的复信号xt(n)=α(n)+j⋅β(n)，n=0，1，…，Ns-1，其中实部α(n)与虚部β(n)均服从均值为0、方差为n0/2的高斯分布，且二者互不相关。按照随机变量分布的相关性质，2个独立同分布的0均值高斯随机变量的平方和再开方之后所生成的新随机变量服从瑞利分布，所以复信号xt(n)的模值，记为zn=‖ ‖xt(n)，服从如下的瑞利分布：

由式（1）可得，zn的均值为(πn0/2)12，方差为(2-π/2)n0。

对于复信号xt(n)的每一个时域采样点来讲，其时域宽度 Δt=1/fs，频域宽度 Δf=fs，满足 Δf⋅Δt=1，所以复信号xt(n)的每一个采样点同样对应了一个单位面积为1的时频块。

在上述分析中只考虑了噪声分量单独存在的情况，如果在时频块上还存在目标信号分量，由于单位面积时频块是时频面上的最小可分辨单元，所以目标信号分量可等效建模为正/余弦信号。根据随机过程的相关性质：正/余弦信号加上高斯随机信号之后包络服从莱斯分布，又称为广义瑞利分布，于是单位面积时频块上的噪声与目标信号之和所生成新的随机变量的模值zn+s服从如下的莱斯分布：

式中，I0(·)是修正的0阶第一类贝塞尔函数，KL=Es/n0表示单位面积时频块上的目标信号能量与噪声能量之比，称为莱斯因子；当KL=0时莱斯分布退化为瑞利分布。

实际上，在不同时频尺度的单位面积时频块上无论是噪声，还是再叠加了目标信号，在工程应用中获得其信号模值的常用方法是通过短时傅里叶变换来得到，记X(kf)为复信号xt(n)的频域频谱，kf=0，1，…，Ns-1，可表示为：

由于多个同分布的高斯随机变量的线性叠加仍然服从高斯分布，所以在仅存噪声的情况下，X(kf)服从高斯分布。针对式（3）可求得频域频谱X(kf)的均值和方差分别为：

式（4）中E(·)表示求随机变量的数学期望函数，式（5）中var(·)表示求随机变量的方差函数。由上可见：X(kf)的均值为0，方差仍然为n0。将2个不同序号的X(kf)进行相关运算，可得：

由式（6）可知：零均值的2个频域高斯随机变量互不相关，则意味着这2个高斯随机变量相互独立。式（4）—（6）实际上已经证明：在式（3）定义的离散傅里叶变换之后，Ns个时域采样点的复噪声信号xt(n)对应的Ns个频域频谱分量X(kf)仍然是独立同分布的零均值高斯随机变量。

2 n0的测量与接收G/T值之间的关系

一个实际接收系统中，在接收通道的不同位置处放大增益不同，在对信号进行放大的同时也会放大噪声，所以在接收通道的不同位置处测量出的单位面积时频块上的噪声平均能量n0显然是不同的。为了获得统一的度量尺度，参照接收系统G/T值的测量方法，将天线馈线后端与接收机入口处相连接的位置作为参考点，将接收机中的整个噪声也等效换算到接收机入口处，并与天线和馈线输出的噪声叠加在一起来综合测算在此处的噪声平均能量，以此作为整个接收系统的n0，如图1所示。

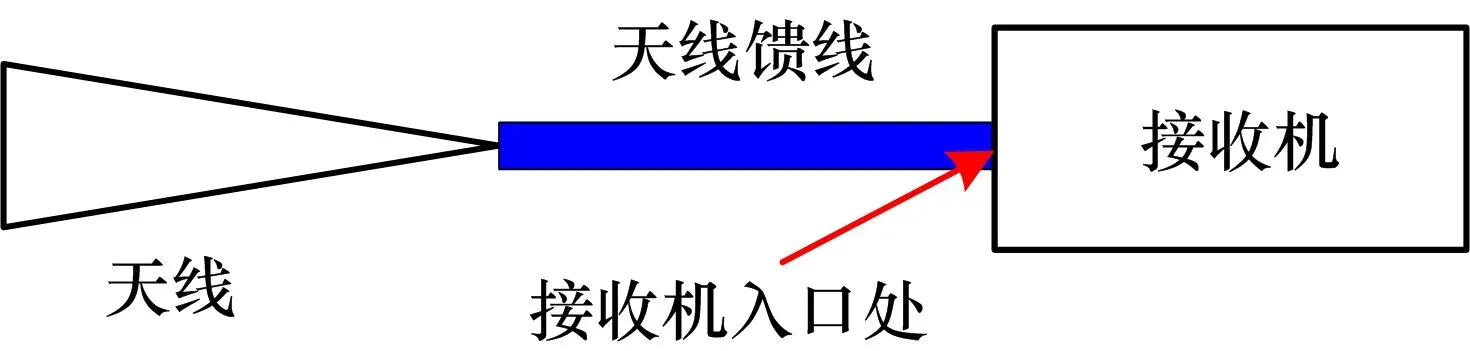
图1 接收系统中n0与G/T的测量位置图示

实际上接收系统G/T值的测量也采用了类似的方法与流程，在接收机入口处G表示了在考虑接收天线增益与馈线损耗条件下从天线到此处的通道总增益；而T表示了天线噪声、馈线噪声与接收机等效噪声三者叠加所综合形成的噪声温度。如果一个接收系统的G/T值越大，在给定接收带宽范围内所接收到的信号的信噪比就越高，这无论是对于通信传输，还是雷达探测等工程应用来讲，都意味着接收性能越好。而增大G/T值的2个基本途径为：一是提升接收天线的增益，降低接收馈线的损耗，从而使G得以增加；二是降低天线噪声、馈线噪声和接收机的噪声，使综合噪声温度T得以减小。从高频到毫米波频段范围内，n0与噪声温度T之间存在如下关系式：

式中，k=1.380 54×10-23J/K表示玻尔兹曼常数。所以在工程上只要测量得到了接收机入口处的综合噪声温度T，便可由式（7）换算得到单位带宽内的噪声功率，即单位面积时频块上的噪声能量n0。

假设到达接收系统天线入口处目标信号的能量为Ein，a，由接收系统的G/T值便可计算出接收机入口处信号的能量信噪比Esig/n0，如下所示：

由式（8）和式（7）可知，表征接收系统性能的G/T值与接收信号的能量信噪比Esig/n0成正比，而其中的综合噪声温度T又直接决定了接收机入口处的n0值。所以n0和G/T值从不同的角度反映了接收系统的性能，二者也成为工程应用中评估接收系统性能的重要参数。

3 匹配滤波中信号与n0之间的关系

众所周知，如果要在最大信噪比条件下对信号xtc(t)进行检测，则匹配滤波器是最佳选择。匹配滤波器的时域响应波形htc(t)与被检测信号在时间上共轭对称，即htc(t)=x*tc(τ0-t)，其中τ0为时移参考时刻，匹配滤波输出的信号能够达到信号的最大能量信噪比Esig/n0。这一经典结论在各类有关信号分析处理的教科书中都有详细的推导与论证，而且几乎都采用了许瓦兹不等式的等号成立条件来解释匹配滤波器的设计要点，本文不再赘述。在此利用单位面积时频块上的噪声分布特性，从信号相干积累的角度来对匹配滤波的效果进行新的解释。

如前所述，AWGN加性白高斯噪声按照式（3）由时域变换至频域之后仍然保持了与时域一样的分布特性，即单位面积时频块上的噪声能量仍然为n0。假设采样信号分量经过式（3）的变换之后散布于Nf个单位面积的时频块上，其能量信噪比分别记为：Es，j/n0，j=1，2，…，Nf，且有：

将上述Nf个单位面积时频块上的信号分量进行加权求和，而加权系数取为对应的单位面积时频块上信号分量的共轭，于是信号分量加权求和的幅度ys的结果在数值上等于信号的总能量Esig，即ys=Esig，在效果上相当于对信号进行了相干积累。由于信号与噪声之间互不相关，所以噪声分量加权求和之后所生成的随机变量γnoise仍然满足零均值高斯分布特性，但其方差σ2γ=Esign0。经过上述处理之后，新产生的信号的能量与噪声方差的比值如下：

由式（10）可知，在时频域对信号分布的单位面积时频块上以信号分量的共轭加权求和同样也能实现最大能量信噪比的检测效果。上述过程相当于在频域对目标信号进行了匹配滤波，各个单位面积时频块上的信号分量在此过程中得以相干积累，积累之后的能量相当于原有能量的平方关系，而噪声分量互不相关，所以在方差求和过程中只实现了原有能量的一次方关系。由此可见，通过单位面积时频块上的信号与噪声的特定加权处理同样能够达到匹配滤波的目的。

4 时频单元格的划分与信号检测

虽然单位面积时频块是工程应用中时频面上的最小可分辨单元，但在面积保持一定的情况下，不同的时宽与频宽将展现出不同的形状与不同的时频尺度，而这对于信号检测所产生的影响也有差异，接下来对此进行更加详细的讨论。

4.1 单位面积时频单元格的不同划分方式

在短时傅里叶变换式（3）中，当Ns=1时，X(0)=xt(0)，这实际上就对应了前述的时域采样点，此时时域分辨率最高Δt=1/fs，而频域分辨率最低Δf=fs，但仍满足时频块的面积为1的特性，即Δf⋅Δt=1。随着式（3）所包含的时域采样点数Ns的逐渐增大，通过式（3）变换之后信号的时域分辨率Δt逐渐下降，依次演变为 2/fs，3/fs，4/fs，……，而频域分辨率 Δf逐渐增大，依次演变为fs/2，fs/3，fs/4，……，但是无论如何变化，始终保持Δf⋅Δt=1的特性。以Ns从1变化至8为例，绘制上述不同时频尺度的单位面积时频块的演变过程，如图2所示。

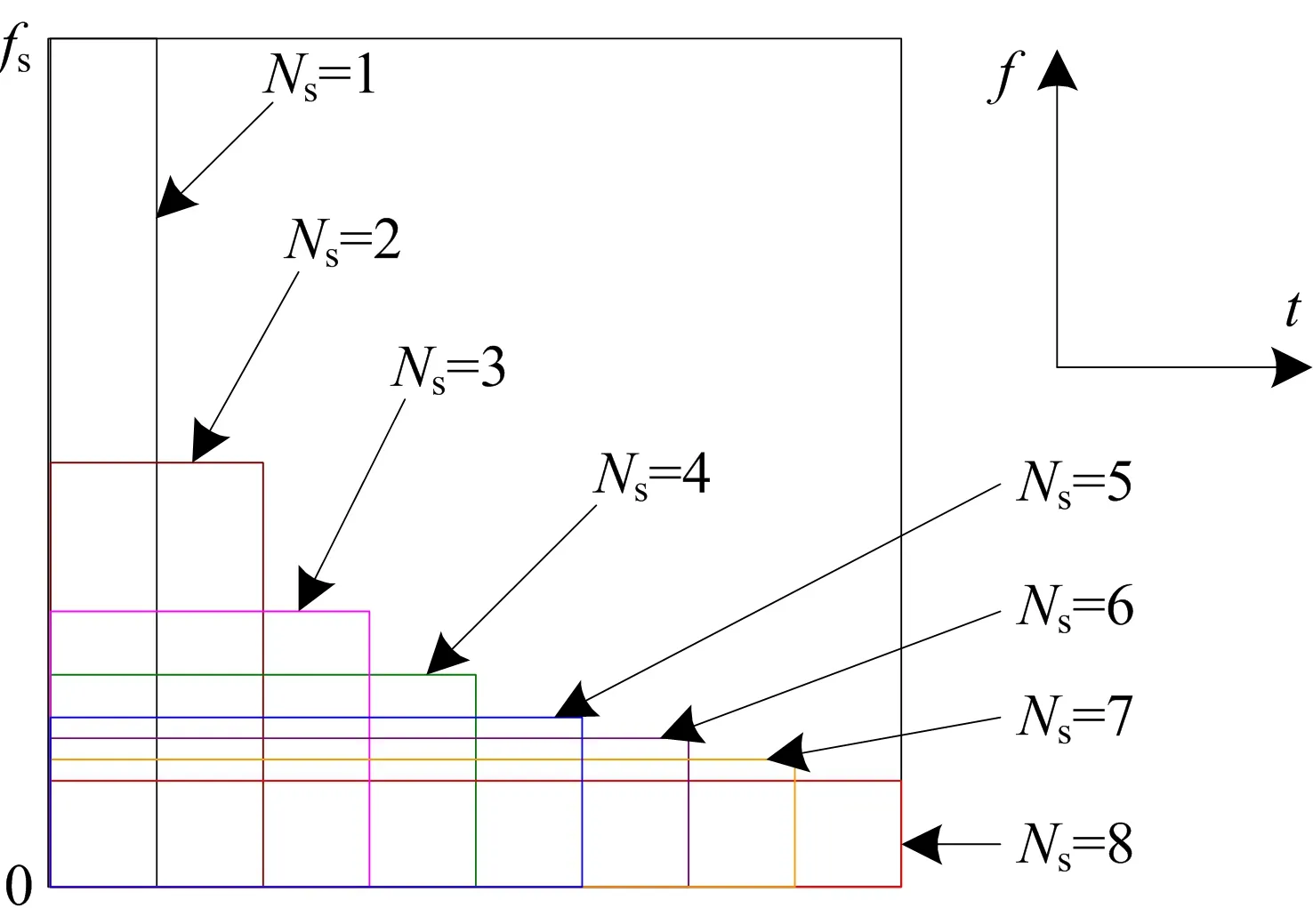
图2 不同时频尺度的单位面积时频块演变过程

图2展示了不同时频尺度的单位面积时频块在时频面上的相对位置与比例关系，如果所关注区域对应的时频面的总面积为Stf，则可以将其划分成Stf个单位面积的时频块。由图2可知，不同时频尺度的单位面积时频块构成这个时频区域的方式不一样，但是时频块的个数都是Stf个。以Stf=12为例，用6种不同尺度的单位面积时频块来填充这一面积为12的时频区域，如图3所示。

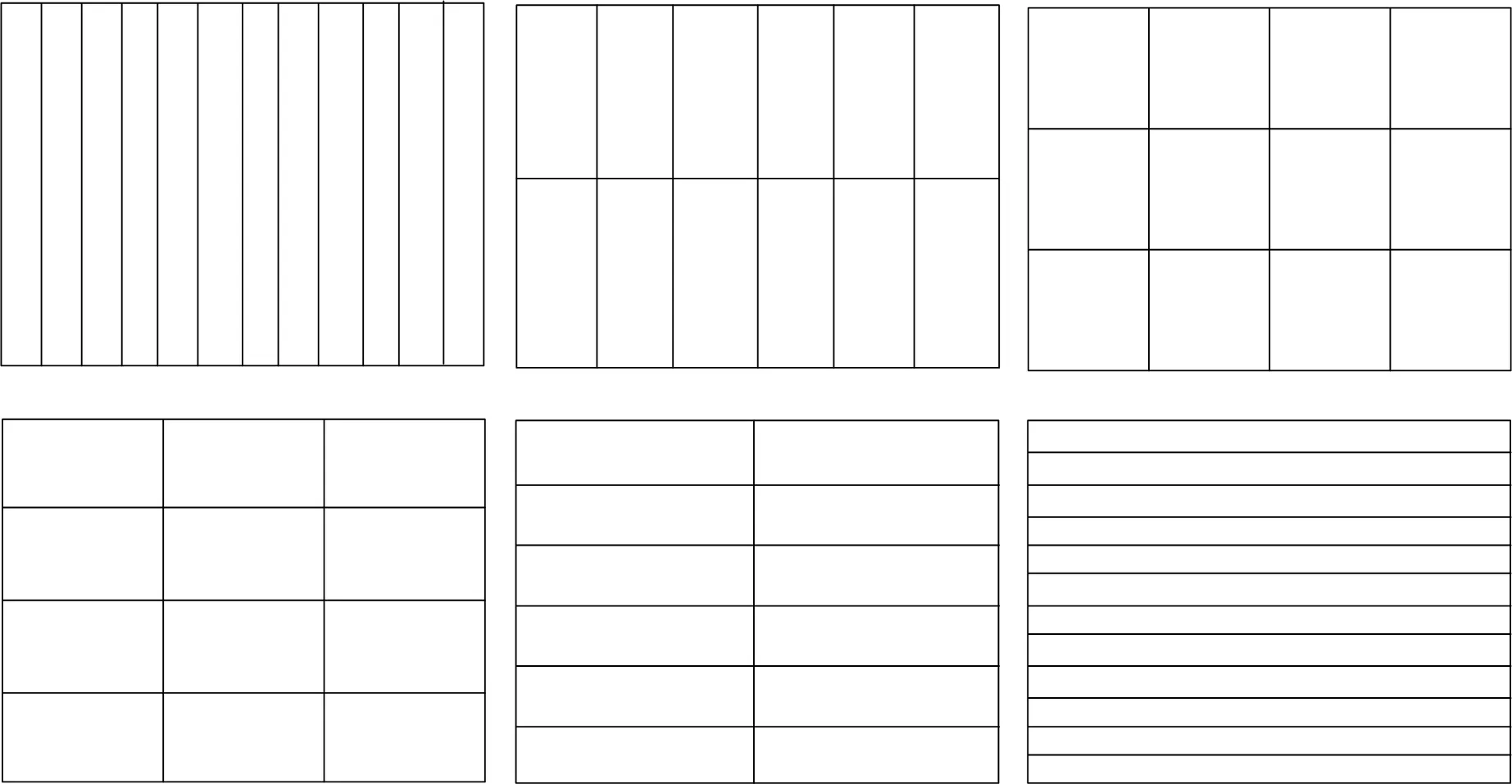
图3 以6种不同尺度的单位面积时频块进行划分

按照上述分析结果，图3中的时频区域在时间维度有12个采样点，在频率维度的采样频率为fs，以6种不同尺度的单位面积时频块对总面积为12的时频区域进行划分，尽管划分方式不同，但是每一种单位面积的时频块均满足前述的噪声与目标信号的相关统计分布特性，因为按照离散傅里叶变换式（3），每一个单位面积时频块上的信号X(kf)是由Ns个独立同分布的高斯随机信号通过式（3）线性叠加而成，所以仍满足独立同分布的高斯分布。

4.2 在单位面积时频单元格上检测目标信号

如前所述，单位面积时频块上如果只有噪声信号时，综合后信号的模值服从均值为(πn0/2)12，方差为(2-π/2)n0的瑞利分布；存在噪声与目标信号叠加时，综合后信号模值服从莱斯因子KL=Esig/n0的莱斯分布，如图4所示。于是在时频面的单位面积的时频块上以噪声基底作为参考，按照奈曼·皮尔逊准则，以一定的虚警概率划定判决门限，凡是信号模值超过门限的单位面积时频块即可判定为其上存在目标信号分量。

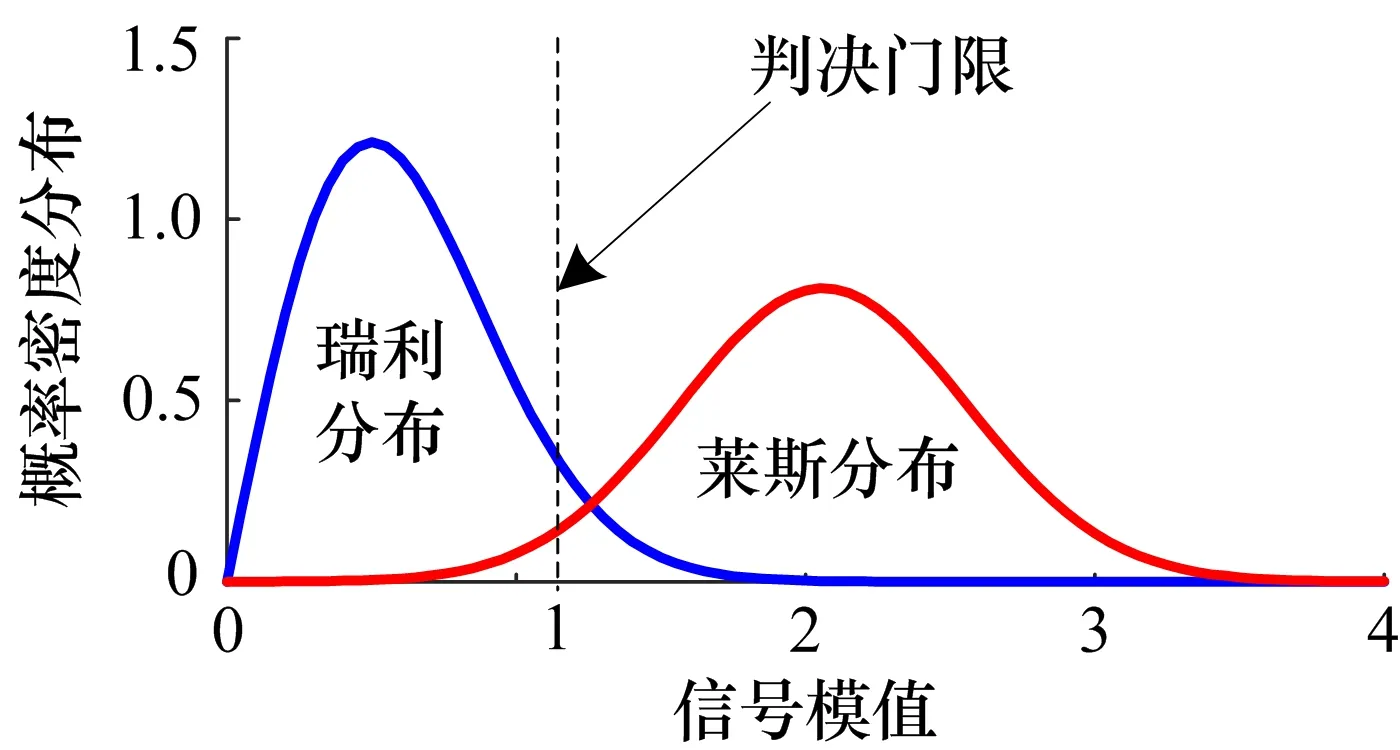
图4 单位面积时频块上的信号模值分布概率示意图

从理论上讲，虽然该信号检测方法具有较好的性能，但是其达到理论检测性能的前提条件是目标信号分量已经完全占据了整个单位面积时频块，才能以较高的概率完成信号的有效检测。在AWGN加性高斯白噪声条件下，虽然噪声信号在单位面积时频块上的统计特性只与时频块的面积有关，与时频块的尺度无关，但是目标信号的分布却与时频块的尺度有关，而且对于处于非合作地位的侦察方来讲，目标信号的频率与持续时间都是事先未知的，所以为了使单位面积时频块与目标信号尽可能地相互匹配，就需要按照图2的划分方式在时间维度上逐渐改变单位面积时频块的时间尺度与频率尺度，用不同尺度的时频块去填充需要进行目标信号检测的时频区域。由图2可知，如果遍历划分所有尺度的单位面积时频块将给工程实现带来极大的计算负担，虽然这一方式也可用于事后处理的信号情报侦察类应用，但难以在有实时性要求的工程项目中使用。为了在计算量与检测性能之间取得平衡，借鉴小波分析中多分辨率等比分级的思想，以2倍等比尺度划分为例进行工程应用的实现，可以在一定程度上解决该问题。

4.3 基于等比尺度分级划分的时频分析工程实现

工程上的短时傅里叶变换通常利用快速傅里叶变换（FFT）来实现，而且在现场可编程逻辑阵列（FPGA）中有长度为2的整数次幂的FFT⁃IPcore能够实时流水实现FFT的计算。鉴于此，通过多个2的整数次幂长度的FFT来实现时频面的多种时频尺度的单位面积时频块的实时流水划分，如表1所示。

表1 各种时频尺度的单位面积时频块

表1中仅列出了幂指数取值从0到7的情况，实际上幂指数的最大取值Me，max取决于需要检测信号的最小带宽Δfmin，由下式计算：

式中，ceil(·)表示向上取整运算符。在FPGA中调用Me，max个FFT⁃IPcore即可完成尺度按照2的整数次幂变化的单位面积时频块的实时流水合成。由于目标信号所占有的总时频面积始终大于等于1，所以按照上述分级划分方法，即便目标信号的时频面积取最小值1，也总能确保在其中一个对应等级的时频单元格中获得至少不小于1/4面积所承载的目标信号能量，如图5所示。

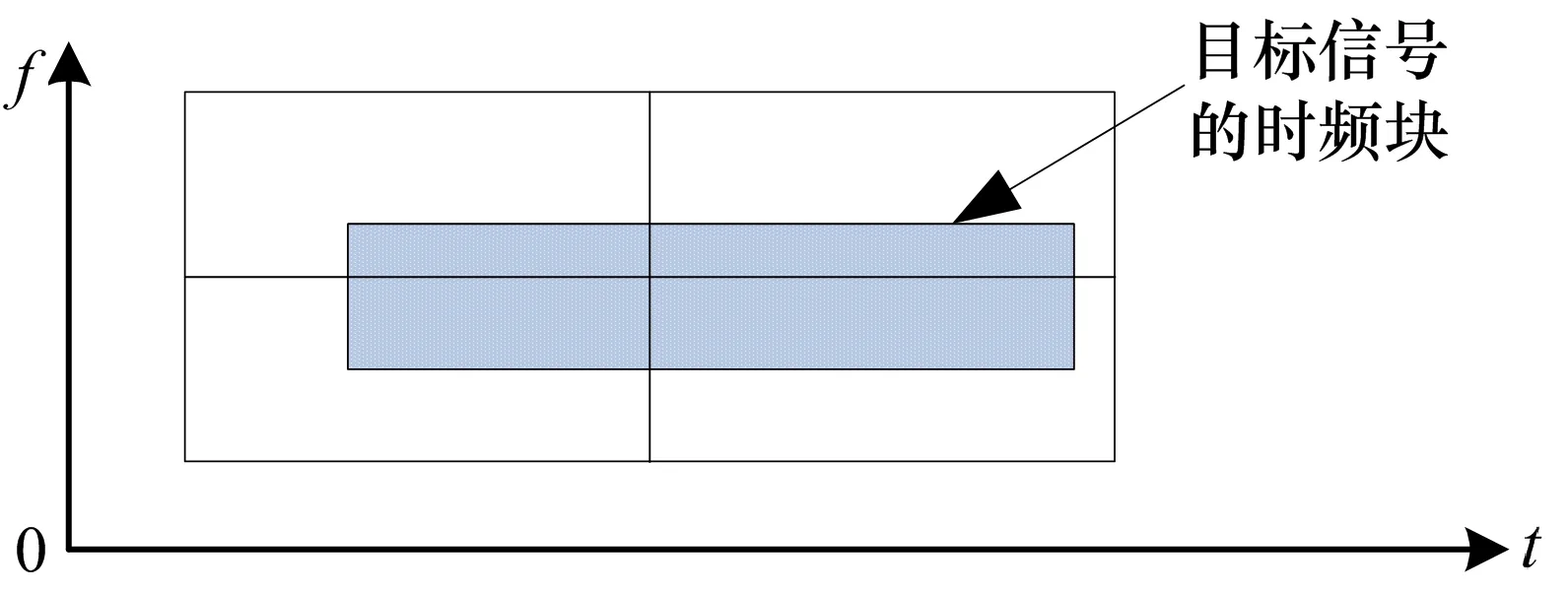
图5 时频单元格划分对目标信号的覆盖情况示意图

图5中每个空白小矩形代表一个面积为1的时频单元格，其时频尺度分别记为 Δtk和 Δfk，且Δfk⋅Δtk=1，阴影矩形代表面积为1的目标信号时频块，其时频尺度分别记为 Δts和 Δfs，且 Δfs⋅Δts=1。当目标信号时频块的频率尺度变化时，一定有一级时频单元格满足0.5Δfk≤Δfs≤Δfk，于是在该级时频单元格划分中，在时间维度上观察也会有0.5Δtk≤Δts≤Δtk成立。于是有：

由此可见，通过2的整数次幂的等比尺度分级划分之后，总能确保在对应尺度等级的其中一个时频单元格中超过1/4的面积被待检测的信号所覆盖，按照前述恒虚警检测所划定的检测门限对该时频块进行判决，即可检测出目标信号。这一方法虽然以漏警概率的少许增加为代价，但是可满足工程上对目标信号实施实时恒虚警检测的要求，这对于非合作的突发性脉冲信号检测类应用具有重要意义。

5 结束语

n0不仅体现了单位带宽内的噪声平均功率，而且反映了时频面上单位面积时频块上的噪声平均能量，是时频分析中噪声特性的重要统计特征参数。本文对n0的测量、n0与接收系统G/T值之间的关系，以及匹配滤波对信号与噪声的不同作用效果进行了详细的分析，展现了单位面积时频块上的噪声统计量在信号检测中所发挥的重要作用。在此基础上针对单位面积时频块上的恒虚警信号检测问题，讨论了时频面上单位面积时频单元格的不同划分方式所产生的不同检测效果，提出了按照2的整数次幂的等比尺度分级划分的时频分析工程实现方法。上述研究结果不仅深刻揭示了n0的本质物理意义，而且为与时频分析相关的信号检测类应用的工程实现提供了方法上的指导。