混合布阵干涉仪系统误差标校方法研究

马 琴，张永强，苏 抗，赵巾卫

（1.中国航天科工集团8511研究所，江苏 南京 210007；2.北京跟踪与通信技术研究所，北京 100094）

0 引言

干涉仪测向定位系统通过测量位于不同波前的天线接收信号的相位差，处理获取辐射源来波方向（DOA）［1］，进而完成陆、海面辐射源位置估计。其系统结构简单、设备量少、定位精度高，通过单个观测站截获单脉冲即可完成测向定位，在电子侦察技术领域得到了广泛应用。干涉仪测向定位系统天线阵通常由多个天线阵元组成，常用的天线布局有圆阵、正交线阵或正交L阵等多种形式，也有测向系统采用圆阵和正交线阵混合布局，这种布局可以获得更高的定位精度和解模糊概率，也更有利于系统误差标校。

干涉仪测向定位系统测量得到辐射源信号到达时间、信号频率、接收通道间相位差等信息后，利用测向算法获得辐射源来波方向。针对陆、海面辐射源，以时间为基准对观测站位置信息、姿态信息进行插值后，根据二维来波方向确定辐射源-观测站视线与地球表面交点，即可完成辐射源位置估计。上述观测信息接收通道间相位差、姿态信息及天线位置系统误差对系统性能影响较大，会造成显著的定位偏差和解模糊概率下降。

为精确估计系统误差，通常需要开展系统误差标校工作。标校方法为利用地理位置精确已知、信号特征参数已知的标校源发射信号，观测站接收标校源信号后完成参数测量并获取相位差数据，通过数据处理完成系统误差估计，并对上述观测信息进行修正等，降低系统误差对定位精度和解模糊概率的影响。

本文根据现有测量手段，结合混合布阵干涉仪系统特点，简化了系统误差理论模型，并通过理论仿真和实测数据处理进行算法验证，结果表明该方法可以精确估计系统误差，有效提高干涉仪系统定位精度和解模糊概率。

1 混合布阵干涉仪定位系统误差分析

根据测向、定位处理流程中各信息使用情况可知，定位误差主要受定位相关参数测量误差、天线位置安装误差和相位一致性误差等几类误差影响。下面逐一分析各项误差对定位精度的影响。

1.1 参数测量误差

1） 时间误差

目前干涉仪测向定位系统通常采用“北斗”/GPS导航接收机输出的秒脉冲进行时间同步，同步精度一般优于100 ns；脉冲到达时间测量误差和采样时钟、信噪比等有关，目前典型的干涉仪测向系统脉冲到达时间测量精度优于50 ns；定位系统本地时钟稳定度优于10 ppm。综上可见，时间测量综合误差约为十微秒量级，等效引入位置误差小于米级，对定位误差影响可以忽略不计。

2） 观测站位置误差

观测站位置误差会造成辐射源定位结果整体偏移，采用高精度“北斗”/ GPS导航接收机进行观测站精确定址，位置测量精度可精确到50 m左右，对定位误差影响较小，可忽略。

3） 观测站姿态测量误差

干涉仪测向定位系统通常配备高精度姿态测量设备，姿态测量精度一般可优于0.01°（3σ），该项误差对定位误差影响约为百米量级。

4） 信号频率测量误差

接收机采用RIFE等算法进行频率精确测量，测量精度可优于0.5 MHz，对辐射源信号频率为1 000 MHz，相对频率测量误差小于0.000 5。根据误差传导关系可知，等效相位差测量误差小于1°，对测向精度影响较小，可忽略。

可见，上述4项误差对定位精度影响可以忽略，不需要进行校正。

1.2 相位误差

相位误差引起的测向定位偏差通常较大，以相位误差15°为例，假设干涉仪基线长度为1 m，针对频率1 000 MHz的辐射源信号，测向误差约为0.7°@法线方向~1.4°@60°入射方向，该项误差对定位精度影响较大，应予以考虑。引起相位误差的因素包括单元天线相位一致性误差、接收通道相位误差及射频电缆相位一致性误差等。

1） 单元天线相位一致性控制

天线单元的相位一致性，主要通过控制天线加工精度、增加投产比例以严格筛选相位一致性好的天线进行配对等途径进行控制。

2） 接收通道相位一致性误差

干涉仪测向系统接收通道相位误差主要由通道间电长度、温度等不一致引起。常温下接收通道系统误差、射频电缆相位一致性误差可在实验室条件下进行测量、修正，部分通道误差可设计实时校正链路，通过设置内部校正源实时校正，但仍有部分链路存在的系统误差无法在实验室环境下测得，需要进行标校。

1.3 天线安装误差

混合布阵干涉仪系统采用圆阵和正交线阵混合布局，图1给出了一种混合布阵方案，由若干个圆阵天线单元和4个十字阵天线单元组成。圆阵天线单元通过刚性连接方式安装在同一天线安装板，构成若干短基线干涉仪。天线安装板通过刚性连接方式固定安装于观测平台。天线安装板相对观测平台安装关系在实验室条件下进行了标定，标定过程中存在测量误差，加上实际工作时由于振动及周围环境的变化，坐标转换矩阵偏离标定值，因此需要重新估计。

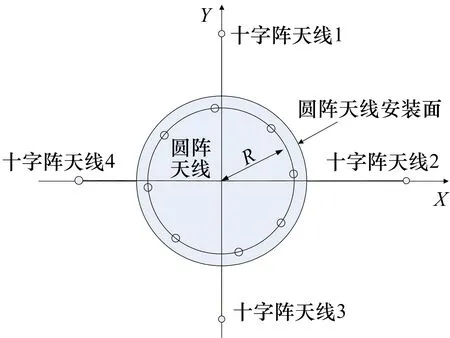
图1 雷达侦察天线布局

圆阵天线安装于同一安装板，天线单元间构成短基线干涉仪用于解相位模糊，其安装精度可以通过结构设计与机械安装得到保证。十字阵天线构成的基线较长，机械安装环节多，安装精度难以保证，实验室条件下现有的测量手段难以获得其精确位置，加上振动、变形等因素，均可导致天线偏离理论设计位置。因此，十字阵天线位置系统误差需要通过采集数据进行标校。

综上所述，需要进行标校的系统误差项包括十字阵天线安装位置误差、圆阵天线安装板与观测站本体之间的转换矩阵及比相接收通道相位系统误差三项。本文提出系统误差分步标校方法，即先标校旋转矩阵系统误差，再标校天线位置和通道相位系统误差。

2 系统误差标校方法

2.1 “参数法”标校方法

干涉仪测向通过测量位于不同波前的天线接收信号的相位差获得辐射源来波方向，k时刻接收天线i，j侦收同一辐射源脉冲信号的相位差可表示为：

式中，λ表示辐射源信号频率，N表示干涉仪天线单元数，RBI表示干涉仪天线安装面坐标系到观测平台本体坐标系旋转矩阵，Xi，j表示干涉仪基线矢量，ηk表示观测平台坐标系下目标视线矢量。

假设在干涉仪坐标系下天线i的坐标表示为Xi，天线j的坐标表示为Xj，则基线矢量Xi，j可表示为：

假设侦收辐射源脉冲时刻k在定位坐标系下辐射源坐标为Xkt，观测平台位置坐标为Xko，在定位坐标系下目标视线矢量ηk可表示为：

式中，‖-‖为取模运算，表示k时刻辐射源到观测平台距离。

根据定位误差影响因素分析，干涉仪天线安装面到观测平台本体坐标系之间存在固定偏差，坐标原点之间相对位移对干涉仪系统定位误差影响不大，本文仅考虑旋转矩阵之间的系统偏差，即假设干涉仪天线安装坐标系和观测平台本体坐标系坐标原点重合。接收通道i与接收通道j之间相位差系统误差为Δϕi，j，十字阵天线 1、2、3、4 位置为Xi，i=1，2，3，4，系统误差ΔXi引起的测向偏差通常较大，应加以考虑。系统误差简化模型为：

式中，表示干涉仪天线安装面到观测平台本体坐标系旋转矩阵真值表示k时刻坐标天线i、天线j构成的干涉仪接收通道相位差真值表示天线i位置真值，相位差计算模型可表示为：

天线安装面坐标系到观测平台坐标旋转角度定义为ψ（绕Z轴），θ（绕Y轴），φ（绕X轴），旋转关系如图2所示。

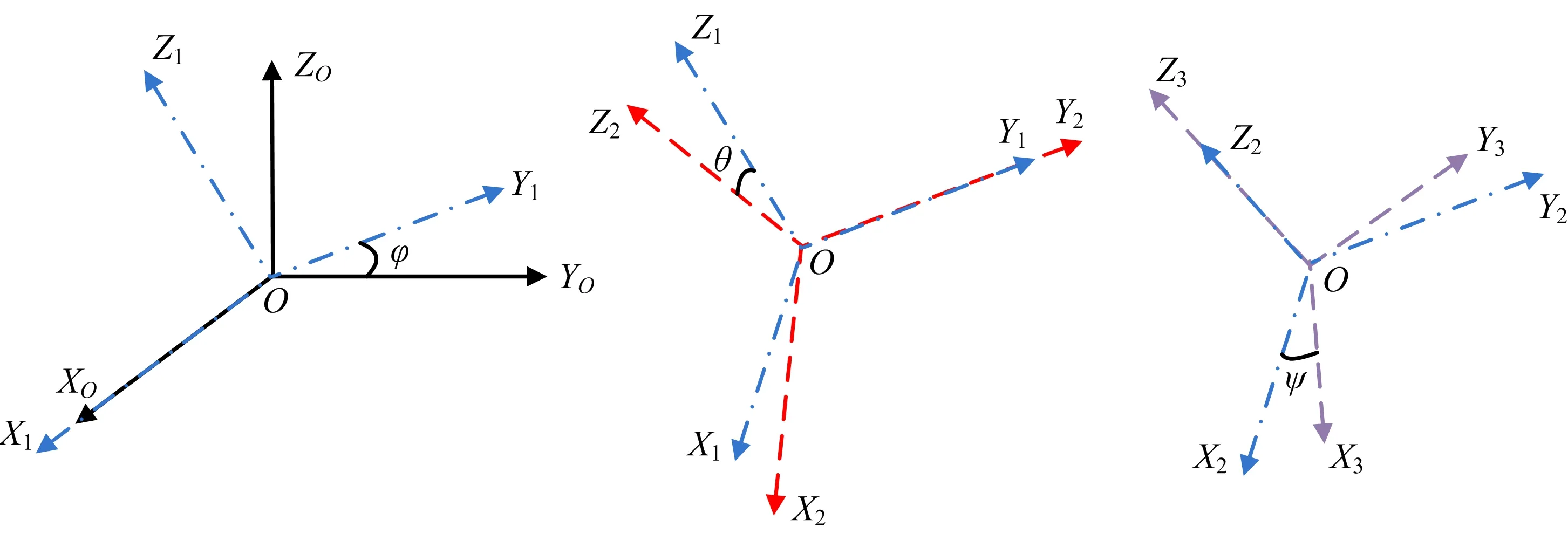
图2 天线安装坐标系到观测平台坐标旋转矩阵系统误差示意图

坐标转换矩阵的标准形式如下：

ΔXi，j表示干涉仪基线中以i天线坐标为基准、天线j在干涉仪天线安装坐标系下三轴坐标系统误差，ΔXi，j=[Δxj，Δyj，Δzj]T，Δϕi，j表示通道ij相位差系统误差。

圆阵单元天线通过刚性连接固定安装在天线安装面，其在天线安装坐标系下的位置在实验室进行了严格的标定，低轨卫星或空中观测平台天线安装面使用过程中受热、振动等因素引起的变形量较小，因此圆阵单元天线位置精确已知，可认为是已知量。

首先利用圆阵单元天线位置已知信息，估计干涉仪天线安装面到观测平台本体坐标系之间系统误差。圆阵单元天线通道间干涉仪相位差可表示为：

通过多次侦收获得相位差序列写成矢量形式可表示为：

系统误差用矢量形式表示为：

将式（7）进行泰勒展开，保留一阶近似项可得：

可得系统误差矢量最小二乘估计值，表示为：

式中，Δ0为系统误差矢量初始估计值，一般设为全零。得到第一步估计值̂后，令 Δ0=̂，Δ =̂进行最小二乘迭代，提高系统误差估计精度。

然后，完成十字阵长基线天线位置及通道系统误差估计。

十字阵天线i在观测站本体坐标系下系统误差表示为 Δxi、Δyi、Δzi，圆阵与十字阵通道相位系统误差表示 为 Δϕm，i，m=5，…，N，i=1，…，4，用 矢 量 形式表示为：

观测方程表示为：

式中，ΔXm，i为以天线m为基准、天线i位置系统误差，三轴误差分别为 Δxi、Δyi、Δzi，ϕkm，i为第k时刻通道m、i间相位差测量值，δϕkm，i、δϕi，j为相位差测量随机误差，Δϕm，i为通道间系统误差。多组天线通道测量得到的相 位 差 采 用 矢 量 形 式 表 示 为1，…，4，m=5，…，N，采用最小二乘法估计系统误差，更新系统误差估计值为：

2.2 “建表法”标校方法

当辐射源信号频率较低时，大视角侦收定位时误差较大，采用“参数法”进行系统误差估计并修正后定位精度往往难以满足使用要求。针对这种情况，本文提出建立方位-俯仰-相位差系统误差修正表，用于修正大视角相位系统误差。该方法通过侦收地面标校站辐射的雷脉冲信号，得到实测相位差数据，与理论计算的相位差相减获得残差，短时间内多个脉冲信号的残差取平均，作为该视角下相位差校正值。

k时刻通道i、j相位差的计算模型可表示为：

式中，(ω，ζ)表示k时刻辐射源信号入射方位角、俯仰角。系统误差跟入射视角有关，在某一入射角下系统误差为固定值。包含了天线相位一致性误差、通道相位系统误差、天线位置偏差等因素产生的等效相位系统误差，用 Δϕi′，j(ω，ζ)表示。对于同一入射角度、同一工作频点可以将各项误差统一到等效相位系统误差进行校正。假设通过一段时间观测获得相位差实测序列，通道i、j相位差系统误差可表示为：

式中，(ω，ζ)为根据平台位置姿态、天线实测位置及信号频率、标校源位置等信息计算的理论相位差。

通过平台和标校源相对位置变化，遍历所有不同的信号入射方位角、俯仰角度，采用同样的方法得到各入射角度下的系统误差值，从而建立方位-俯仰-相位差系统误差修正表。

3 标校效果仿真分析

3.1 标校参数估计精度分析

由式（6）、（10）可知，系统误差估计实际上是观测量为相位差、测量参数包括信号频率的非线性估计，其精度取决于相位差测量精度、信号频率等。信号频率越高，系统误差估计精度越高；相位差测量误差越小，系统误差估计精度越高。因此，在实际应用中，标校源可以发射高频段信号，观测平台通过侦收高频段信号相位差来提高系统误差估计精度。

为分析本文提出系统误差估计性能，采用Monte‑Carlo仿真方法统计系统误差估计精度。仿真次数设置为100次，相位差测量误差设置为2°~20（°rms），且相位差测量误差随入射视角增加正弦变化。圆阵天线位置误差设置为0.5 mm（rms），频率测量误差均方根0.5 MHz（rms），地面固定标校站位置误差设置为50 m（rms）。

天线安装坐标系到观测站本体坐标系之间转换矩阵系统误差估计精度如图3所示，系统误差真值设置 为 Δϕi，j=150°，i=6，…，N，j=5，Δα=0.5°，Δβ=0.3°，Δγ=0.9°，从图3中可以看出转换矩阵角度估计误差小于0.003°，通道相位差系统误差估计精度优于1°，表明该估计方法有效，估计精度可以满足干涉仪测向系统使用要求。

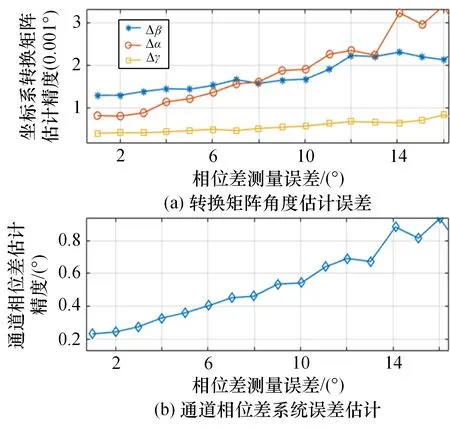
图3 从安装坐标系到观测平台本体坐标系转换误差估计精度

图4给出了天线位置系统误差和通道相位差系统误差估计精度。系统误差设置为Δϕ=200°，Δx=3 mm，Δy=5 mm，Δz=10 mm。从图4中可以看出，当相位差测量误差小于15°（rms）时，通道相位系统误差估计精度优于4°，天线位置估计精度优于0.3 mm。当相位差测量误差大于15（°rms）时，系统误差估计性能迅速恶化。

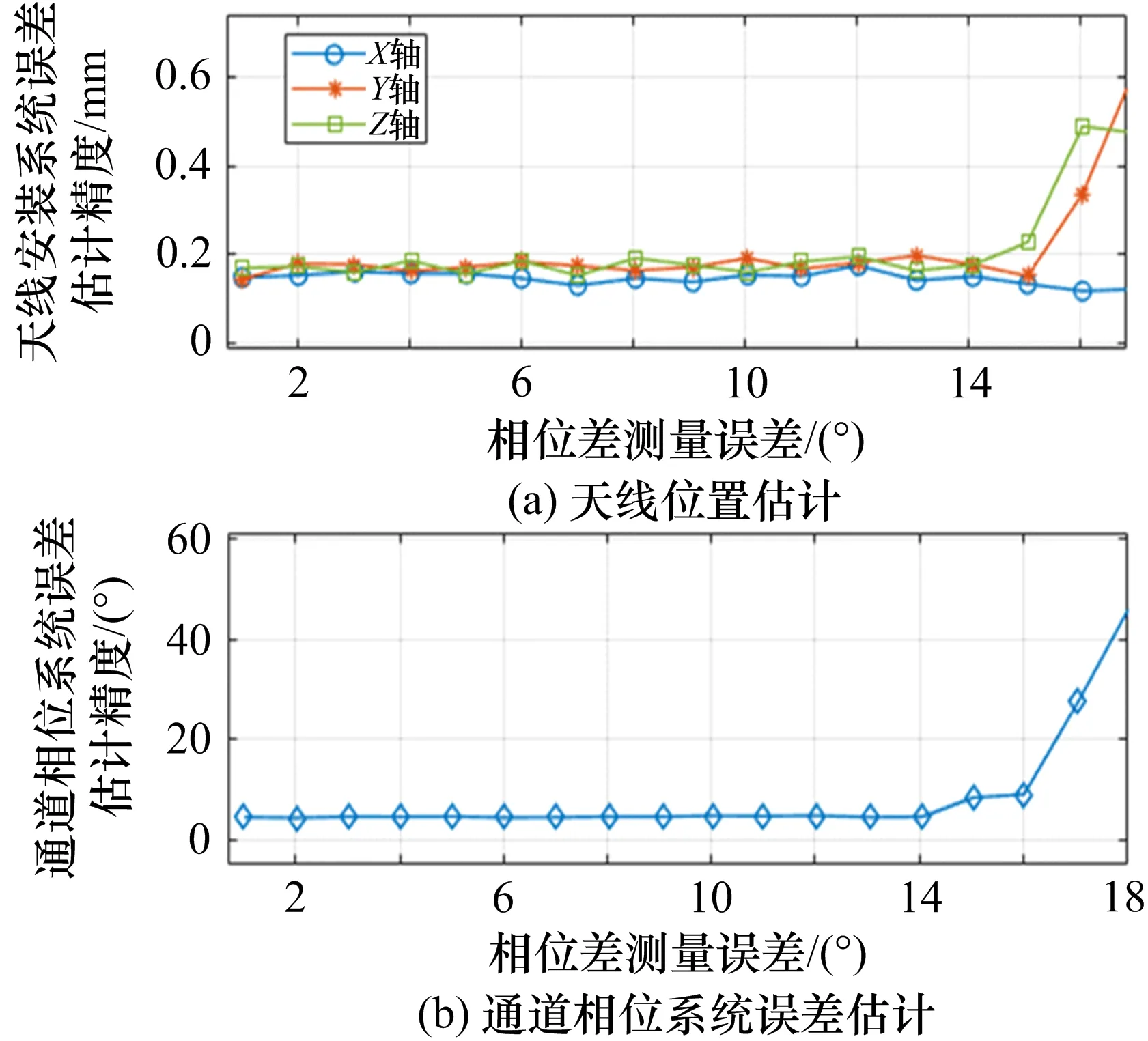
图4 天线位置和通道相位系统误差估计精度

3.2 典型频点标校后定位性能

为验证系统误差标校算法有效性，选取某次标校实验数据，标校前定位结果如图5所示，利用“参数法”估计的通道相位系统误差、天线安装位置偏差对该次观测数据进行修正后定位结果如图6所示。通过对比可见，系统误差未经修正前，标校源定位点偏离真实位置，定位点较为发散，定位精度随着对地视角变大而降低，即更远地偏离辐射源真实位置；通道系统误差、天线安装位置偏差修正后定位点更聚集，且分布在标校源真实位置附近，随着视角增加，定位误差略有增加，但整个视角范围内变化较为平缓。

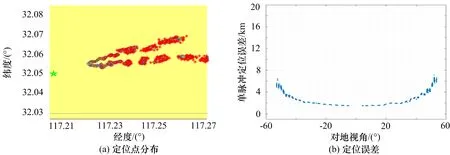
图5 标校前定位点分布、定位误差随着视角变化曲线

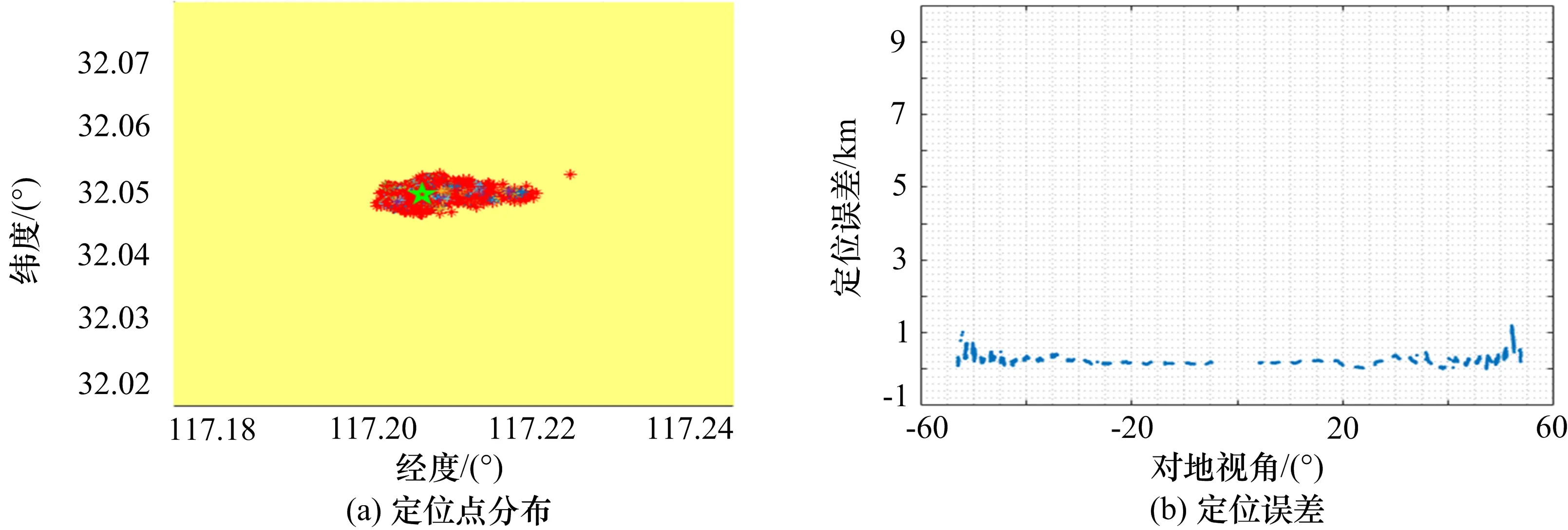
图6 标校后定位点分布、定位误差随着视角变化曲线

3.3 提高标校效率方法

干涉仪系统误差和频率相关。观测站装载的电子侦察设备往往工作频段较宽，工作频段内按照前文2.1、2.2节介绍的标校方法逐个频点进行标校，工作量较大。根据目前标校工作经验，标校参数具有一定的频域扩展性，工作频段内可按照一定频率间隔选取标校频点，减少标校工作量。频段扩展性和干涉仪布局、信号频率及技术指标要求有关。一般来说频段越高，标校参数可扩展性越强。但频率扩展较宽，会造成一定程度地定位精度下降。

其次，观测站一般配置宽带接收机，可分时侦收不同频点标校源信号，同步积累各频段标校样本数据，提高标校效率。

最后，可通过干涉仪系统误差细分，严加控制天线阵元加工、天线阵集成安装工艺等，实现多套干涉仪系统间误差一致性，即可推进标校参数可多套系统公用，革新每套系统逐一标校方式，提高效率。

4 结束语

针对混合布阵干涉仪系统误差标校问题，本文研究了“参数法”、“建表法”等系统误差估计方法，根据混合布阵干涉仪系统特点，提出分步标校方案，即先标校旋转矩阵系统误差，再标校天线位置和通道相位系统误差。针对特定频段大视角系统误差，采用“建表法”进一步提升系统误差标校效果。算法验证结果表明本文方法可以精确估计系统误差，有效提高定位精度和解模糊概率。