基于差分进化算法的异构型分布式阵列优化
付思达,徐慧辉,蒋 明,王铁丹,宁帅宇
(1.中国航天科工集团8511研究所,江苏 南京 210007;2.航天系统部装备部军事代表局,江苏 南京 210028;3.国家电网湖南省电力有限公司,湖南 衡阳 421001)
0 引言
面对复杂的作战环境,如何从海量的战场数据中有效地提取信息并应用,是电子侦察领域面临的难题之一[1]。当侦察平台为卫星、战机等大型载体平台时,不能保证有足够且连续的空间来放置对环境要求较高的传统天线阵列,从而很难在特定的布阵环境下满足阵列天线系统高增益和波束可控的要求,因此分布式阵列应运而生[2]。分布式阵列是一种阵列结构较为特殊的稀疏阵列,由多个子阵构成,子阵与子阵之间的间隔远超过半个波长,子阵构型都相同的叫同构型分布式阵列,子阵构型不全相同的叫异构型分布式阵列[3]。异构型分布式阵列的特点是可在有限的几个区域内放置子阵单元,各子阵单元位于同一载体不连续空间位置所构成的特殊结构,可等效为大口径阵列,从而实现高增益、高分辨率等普通星载机载阵列天线所不能满足的功能。但是,分布式阵列的子阵与子阵之间的距离远远大于半波长,会导致阵列方向性图的主瓣增益降低、副瓣增益升高等问题[4]。所以对分布式阵列进行优化,在保证主瓣增益的同时,降低其副瓣电平具有重要意义。
差分进化算法由于具有易执行、快速收敛、鲁棒性强和全局搜索能力强等优点[5-7],逐渐被用于求解阵列天线的优化问题。目前国内对于分布式阵列优化的研究较少,且优化对象多为同构型分布式阵列[8-14],以异构型分布式阵列为优化对象的文献相对较少。但在实际工程应用中布阵环境相当受限,同构型的分布式阵列有时并不能满足要求,而异构型的分布式阵列布阵灵活,可以根据不同的布阵环境来选择不同的子阵结构。本文在传统的差分进化算法基础上,针对异构型的二维分布式阵列优化问题进行算法改进和建模,并通过仿真验证了该算法的性能。
1 异构型分布式阵列
假设异构型分布式阵列由若干个子阵组成,以其中第一个子阵为例,dx、dy分别是子阵单元的x方向上的阵元间距和y方向上的阵元间距,Dx和Dy分别表示子阵相位中心的x方向坐标位置和y向坐标位置。如图1所示,扩展到三维坐标系,为方便表示,仅画出每个子阵的相位中心坐标。目标位置与坐标原点的连线与xoz面的夹角φ为方位角,目标位置与坐标原点的连线在xoz面上的投影与y轴的夹角θ为俯仰角。

图1 二维分布式阵列模型
对于异构型的二维分布式阵列,假设异构型分布式阵列共有H种不同结构的子阵,则第k种子阵的阵元数目为Mk×Nk,Mk为x方向上阵元个数,Nk为y方向上阵元个数,若扫描角为(θ0,φ0),则第k种子阵的单个子阵方向图表达式如下:
式中,K=2π/λ。第k种子阵的子阵间方向图表达式如下:
式中,Pk表示第k种子阵的子阵个数,Dkxi表示第k种子阵的第i个子阵的相位中心的x方向坐标,Dkyi表示第k种子阵的第i个子阵的相位中心的y方向坐标。根据方向图乘积定理,二维异构型分布式阵列方向图表达式如下:
分析上述表达式,由于Dkxi远大于 (l-1)dx、Dkyi远大于(r-1)dy,则子阵间方向图的变化要比单个子阵方向图的变化快得多,所以子阵间的间距在分布式阵列方向图中占主导地位。因此分布式阵列的优化,可以从子阵的分布位置出发,通过调整各子阵之间的距离,来降低主瓣两侧的峰值旁瓣电平。
2 传统的差分进化算法
差分进化算法主要操作为交叉、变异以及选择。该算法主要采用“个体”间的差异来产生新的个体。在差分进化算法不断迭代的过程中,选择出合适的控制参数的数值是算法成功的关键。基本的控制参数有:种群规模NP、变异因子F、交叉因子CR、最大迭代数Gmax。基本步骤和参数的选取规则如下[15]:
1)初始化:根据具体问题确定解的表达方式和适应度函数,设置种群的规模NP。种群规模越大,就增加了种群的多样性,因为各个个体都存在差异性,所以更有利于寻得全局最优,但是降低了收敛速度。一般来说种群规模NP最优选择在5D—10D之间。
2)变异:差分进化算法通过差分策略实现个体变异,利用几个不同的父代向量做差,产生相应的差分向量,将其向量差缩放后与待变异个体进行向量合成。变异策略可用符号DE/x/y/z表示,其中,x表示当前被变异的个体是随机选择的个体还是种群中最优的个体,y表示使用差分向量的个数,z表示选择的交叉策略,一般指数型交叉策略比较常用。常见的变异 策 略 有DE/rand/1/exp、DE/best/1/exp、DE/current⁃to⁃rand/2/exp、DE/current⁃to⁃best/2/exp等。不同的变异策略具有不同的特点,可根据不同的需求选择不同的变异策略。变异策略中F具有扰动作用,它决定了差分矢量的放大倍数。F取得太大,新一代的变异个体将在一个大的范围中取值,增加了种群的多样性,但是同时也会削弱局部搜索能力。若F取得很小,将会导致个体变异前后没有明显差异,削弱了全局搜索能力,但又利于提高算法的收敛速度。一般来说,变异因子F在初始化过程中设置为0.5,在差分进化的过程中若发现早熟,可增大F,反之则减小F。
3)交叉:交叉操作的目的是通过一定的权重在变异个体和目标个体中随机选择组成新的试验个体。交叉因子CR实际上就表示这个权重,取值范围在0∼1之间。较大的交叉因子可以使试验个体更多地来源于变异个体,反之则更多地来源于目标个体。为了增加了个体之间的差异性,算法初始阶段可以将CR设置为 0.9 或者 1。
4)选择:选择过程主要是采用“优胜劣汰”机制,即比较试验个体于目标个体的适应度值,保留优良个体,淘汰劣质个体。
5)边界条件处理:如果在交叉过程产生的试验个体超出了约束的条件范围,则将这个试验个体剔除掉,重新按照1)初始化一个新的试验个体。
3 算法的改进与建模
3.1 差分进化算法的改进
差分算法虽然收敛速度快、控制参数少、鲁棒性强、全局搜索能力好,但是也存在容易陷入局部最优的缺陷,针对这一问题,目前对差分进化算法主要是从操作算子、种群结构、控制参数和与其它算法相结合这四个方向进行改进。下面本文将根据以上的几个方向,结合分布式阵列的这一应用场景对差分进化算法进行改进,具体操作为:
1)变异策略的改进
本文在变异策略上选择DE/rand/1/exp和DE/current⁃to⁃best/2/exp 两种策略相结合。在差分进化算法的开始阶段,应该侧重于全局搜索能力,充分发挥种群的潜力,保证种群的多样性,DE/rand/1/exp具有寻优范围大的特点,特别适合算法初期。而在算法中后期,应该更侧重于最优个体及其附近区域的局部搜索,DE/current⁃to⁃best/2/exp 则相当实用,它具有寻收敛速度快,有利于局部精准搜索的特点。加入一个权重因子,权重因子随着进化代数的增加呈线性增长,当权重因子较小时,DE/rand/1/exp策略起主导作用,随着进化代数的增加,权重因子越来越大,DE/current⁃to⁃best/2/exp 策略慢慢占据主导作用。另外,在此基础上还可以设置一个调和参数[16],利用扰动策略的思想,随机选择现有的变异操作和扰动策略,进一步增强算法跳出局部最优的能力,调和参数的取值一般大于0.9。表达式如下:
式中,ω为权重因子,取值范围为[0,1],Gmax为总的进化代数,Mr为调和参数,r1、r2、r3为两两互不相同的随机整数且均不等于i,xri,G表示当前种群中随机选取的不同个体,xbest,G表示第G代最优个体。
差分进化算法容易早熟,导致算法停滞,适应度函数值持续不更新。为了解决这一问题,本文提出自适应二次变异的方法,设置一个允许停滞次数的最大值t_max,当种群的最优适应度值连续不更新代数超过t_max,便认为此时算法处于停滞状态,则需要经过二次变异来打破停滞,使进化朝着更好的方向发展。二次变异策略采用种群中的最优个体来决定跳出局部最优的方向,用标准的正态分布来决定跳出局部最优的步长。二次变异表达式如下:
式中,v'i,G+1表示二次变异后的个体。当rand大于0时,新的变异个体朝着全局最优方向移动搜索;当rand小于0时,新的变异个体向全局最优的反方向搜索,有利于探索其它空间的解,加大了算法的寻优范围。
2)选择策略的改进
在选择操作中,引入一个取值范围为0~1的门限值,产生一个随机数,该数的取值范围也为0~1。若该随机数小于等于门限值,适应度值低的个体也会保留至下一代。这样适应度值低的个体也有机会被保存进入到下一代,增加了种群的多样性,尽可能地避免算法在后期陷入局部最优。表达式如下:
如果 rand≥threshold,则:
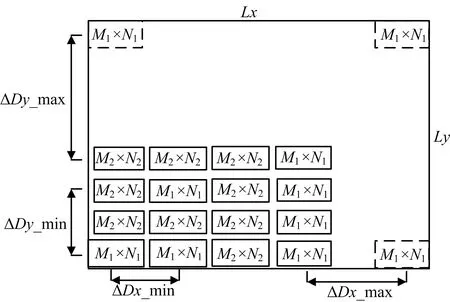
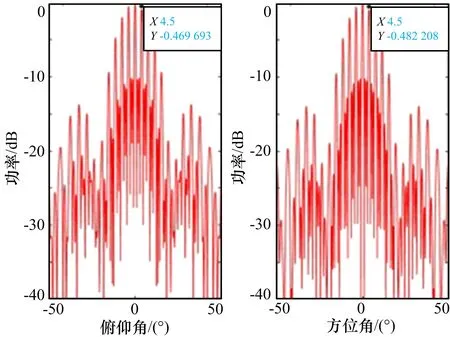
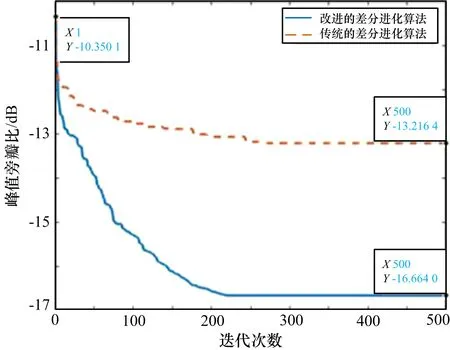
如果 rand 但是随机数和门限值的相对大小存在随机性,有可能会导致本代适应度最高的个体被淘汰,降低了算法的收敛性,所以需要在选择策略中加入替换策略。在每一代种群中适应度最高的个体保存下来,在经过选择操作后,与下一代种群中适应度最低的个体进行替换。这就保证了下一代种群中至少存在一个适应度值等于父代种群中适应度最高的个体。 3)控制参数的改进 为了让F和CR更好地对下一代种群的搜索方向和搜索范围产生影响,参数自适应的差分进化算法逐渐产生。参数自适应是指在算法的不同时期,根据种群的分布情况与适应度之间的相对位置关系来改变F和CR的取值,从而使进化朝更好的方向发展。 本文使参数自适应的方法是将产生优秀个体的参数保留,将产生淘汰个体的参数重新设定。即若下一代适应度优于上一代则控制参数保留,反之则重新设定。表达式如下: 式中,Fi,1为第一代变异因子,Fi,G为第 G 代变异因子,Fmin=0.1,Fmax=0.9,CRi,1为第一代交叉因子,CRi,G为第G代交叉因子。 假设异构型分布式阵列由P个子阵构成,共有n种不同型号的子阵,每种型号子阵个数为Pn,单个子阵列是由Mn×Nn个阵元构成的均匀面阵,最大的面阵记为Mmax×Nmax,则异构型分布式阵列的总阵元个数为子阵内相邻阵元x和y方向的间距dx和dy均为半波长。俯仰角为θ,方位角为φ。 考虑到待求解问题的背景为异构型分布式阵列天线,子阵列的结构并不相同,为了使分布式阵列子阵间不存在阵元相互重叠的情况,在优化前先规定阵列的初始位置。为了方便说明,令n=2,P1=P2=8,最大的面阵为Mmax×Nmax=M1×N1,优化模型如图2所示。分布式阵列的x方向上阵列口径为Lx,y方向上阵列口径为Ly。Dx_min和Dy_min分别为分布式阵列x 图2 异构型分布式阵列优化模型 和y方向上的子阵最小间距。首先让阵列中的子阵都以最小间距进行排布,记录下此时每个子阵相位中心的横纵坐标Dx和Dy作为阵列优化前的初始位置。偏差间距矢量为ΔDx和ΔDy。由于x和y方向的分布式阵列口径不超过Lx和Ly,所以ΔDx和ΔDy应满足0≤ΔDx≤ΔDx_max,0≤ΔDy≤ΔDy_max。其中: 为了使分布式阵列子阵间不存在阵元相互重叠的情况,在x方向上前一个子阵的偏差间距矢量应小于后一个子阵的偏差间距矢量,这是问题约束的关键。但对于y方向而言并不存在这种约束,因为在x轴方向上不存在重叠关系,所以面阵必定不重叠。最后可得子阵优化后的位置坐标为: 为了从物理上保证最大的阵列孔径,增大阵列的自由度,在矩形区域的对角线位置各布设一个子阵。所以第一个子阵的偏差间距矢量为(0,0),最后一个子阵的偏差间距矢量为(ΔDx_max,ΔDy_max)。可以把每个子阵的偏差间距矢量作为优化对象,则第G代种群SG为: 式中,L为种群规模,染色体SGi为: 这里 (ΔDxGl,k,ΔDyGl,k)表示第k个子阵的偏差间距矢量。在差分进化算法中,采用均匀序列生成集合SG。由于本文的目的是降低异构型分布式阵列方向图的峰值旁瓣电平,所以适应度函数为: 整个算法的流程如图3所示。 图3 基于差分进化算法的分布式阵列优化流程图 假设待优化的异构型分布式阵列有P=16个子阵,子阵种类n=2,每种子阵的个数P1=P2=8,第一种子阵的阵元数目为M1×N1=5×5,第二种子阵的阵元数目为M2×N2=4×4,阵元间距为半波长,波长λ=0.25 m,分布式阵列的总体孔径大小为Lx×Ly=40λ×40λ。设置俯仰角和方位角为0°,俯仰和方位扫描范围为-60°∼60°,扫描步长为 0.1°。接下来,把异构型分布式阵列优化前与优化后的结果进行比较。 首先进行子阵均匀分布时的异构型分布式阵列方向图仿真。子阵均匀分布时的异构型分布式阵列的阵元位置图如图4所示,其归一化俯仰维/方位维方向图如图5所示。 图4 异构型分布式阵列的阵元位置图 图5 归一化俯仰维/方位维方向图 由图5可知,子阵均匀分布时的异构型分布式阵列的方向图存在多个高旁瓣,而且高旁瓣的幅度接近于主瓣幅度。下面根据优化问题,将改进的差分进化算法中所需参数设置为:种群数量NP=200,最大进化代数Gmax=100,分布式阵列x和y方向上的子阵最小间距Dx_min=Dy_min=1.6λ。其余仿真条件与均匀子阵分布的异构型分布式阵列相同。得到优化后的阵元位置图如图6所示,其归一化俯仰维/方位维方向图如图7所示。 图6 优化后的阵元位置图 图7 优化后的归一化俯仰维/方位维方向图 比较图5和图7,不难看出,通过本文差分进化算法优化布阵得到的方向图有效地抑制了峰值旁瓣电平,俯仰维从-0.47 dB下降到了-14.99 dB,方向维从-0.48 dB下降到了-15.14 dB,为工程上的实际应用奠定了基础。由图6可知,优化后的子阵分布主要沿着对角线分布,这是为了使二维阵列的俯仰维和方向维的方向图同时达到最优,因此在实际工程应用中,应尽量选择对角线附近不受限制的区域进行布阵。 由于算法本身存在随机性,因此为了证明此算法的优越性,采用相同的初始化种群,最大进化代数为500,独立重复试验10次后取平均值。图8为异构型分布式阵列分别使用传统的差分进化算法和本文改进的差分进化算法的峰值旁瓣电平变化曲线。 图8 异构型分布式阵列峰值旁瓣电平变化曲线 仿真结果表明,当采用相同初始化种群即初始峰值副瓣电平为-10.350 1 dB时,本文改进的差分进化算法的峰值副瓣电平可以下降到-16.664 0 dB,而传统的差分进化算法只能下降到-13.216 4 dB。除此之外,改进的差分进化算法的收敛速度也明显快于传统的差分进化算法。由此可见,本文改进的差分进化算法,针对分布式阵列天线方向图问题,相比于传统的差分进化算法拥有更佳的性能表现。 本文在传统的差分进化算法上进行改进,并将其应用于异构型分布式阵列优化中,通过对有限的子阵进行位置优化,有效地抑制分布式阵列的峰值旁瓣电平。本文算法在变异阶段将2种变异策略相结合并且提出了二次变异,保证了算法的高效性并防止算法停滞。在选择阶段进一步加强了种群的多样性,防止算法在后期陷入局部最优。最后,使F、CR参数自适应控制,从而使进化朝更好的方向发展。仿真实验表明了该算法在分布式阵列优化问题中的有效性和适用性,它不仅能有效地抑制峰值旁瓣电平,而且相比于传统的差分进化算法,全局搜索能力更强、收敛速度更快。3.2 异构型分布式阵列优化模型
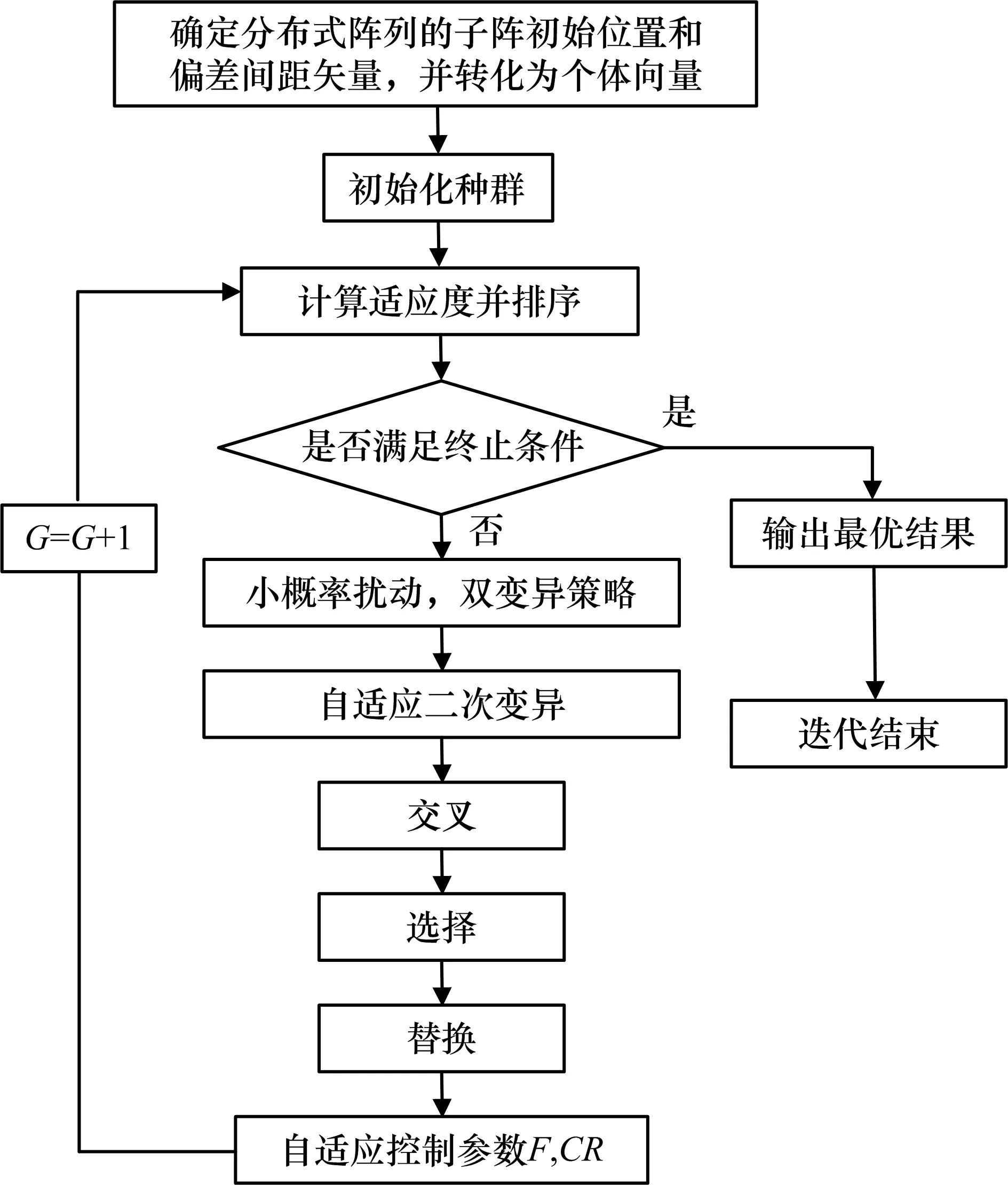
4 仿真实验


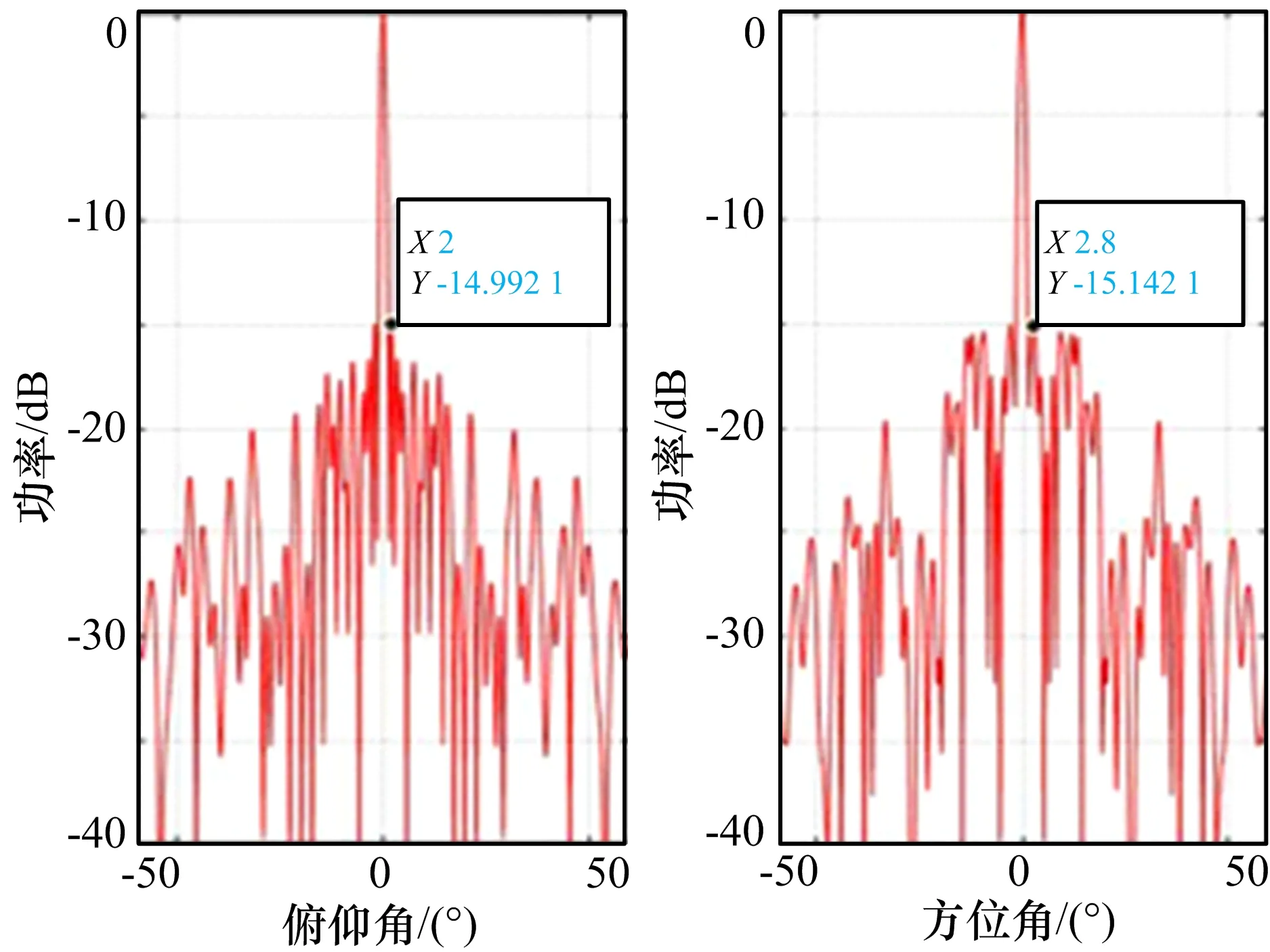
5 结束语

