轮毂电动机驱动滑移转向车辆驱动力控制
付 翔, 赵熙金, 刘道远
(1.武汉理工大学 汽车工程学院, 湖北 武汉 430070; 2.武汉理工大学 现代汽车零部件技术湖北省重点实验室, 湖北 武汉 430070; 3.武汉理工大学 汽车零部件技术湖北省协同创新中心, 湖北 武汉 430070; 4.武汉理工大学 湖北省新能源与智能网联车工程技术研究中心, 湖北 武汉 430070)
滑移转向车辆[1]与阿克曼转向车辆不同,其主要由两侧车轮形成的转速差来实现转向功能.它消除了传统转向系统、传动机构、齿轮等部件,提高了车辆配置的灵活性.滑移转向车辆具有良好的机动性、越野性能、响应能力等优点,可实现原地转向及中心转向功能.目前国内有陆军装备的山猫全地形滑移转向越野车,国外有洛克希德·马丁公司开发的MULE、AMX 10 RC、RAMBOW UGV等滑移转向车辆[2].国内外学者针对滑移转向车辆控制展开了研究.文献[3]在分析对比各种车辆的转向结构和转向原理基础上,提出一种转矩矢量控制策略,准确地对6轮独立驱动滑移转向车辆进行各车轮转矩实时控制分配.文献[4]提出了基于最优控制分配的6WD/6WS驱动控制算法.文献[5]提出了椭圆抛物线接触压力分布的轮胎分析模型,建立了滑移转向车辆在转向工况下的动力学分析模型.文献[6]为了提高滑移转向车辆的机动性和稳定性,提出了一种采用独立驱动电动机的6轮驱动滑移转向电动无人地面车辆的分层驱动力分配和控制策略.文献[7]提出了一种用于滑移转向车辆的鲁棒控制方案,能够在越野路面实现高速路径跟踪.文献[8]提出6WID滑移转向车辆发展的瓶颈是轮胎控制的协调性、控制需求的实时性和组合运动中的动力协调性.协调的车轮转矩控制是实现滑移转向和车辆驾驶控制的关键因素.针对车辆在复杂行驶工况下轮胎路面附着条件复杂多变从而影响动力学控制效果的问题,文献[9]分析了滑移转向车辆的动力学特性,提出了双闭环结构的侧向动力学控制方法.文献[10]考虑滑移转向车辆车轮-地面相互作用和车轮动力学的综合动力学模型,提出了一种基于模型的协调自适应鲁棒控制方案.文献[11]提出了一种松弛静态稳定性动力学控制方法,以过极点配置技术的横摆力矩控制来改善闭环操纵稳定性.
现有的下层电动机转矩分配方法多针对分布式四轮驱动系统,控制分配方法主要分为基于规则的分配方法[12]和针对基于优化的转矩分配方法.在文献[13-14]的4种MIDEV转矩控制分配方法中,与那些最小化能效的目标函数相比,基于最小轮胎滑移准则的目标函数具有更好的控制效果.
由于特殊的转向模式,滑移转向车辆在转向时轮胎会进入侧偏纵滑的复合运动状态,会对轮胎侧/纵向力学特性产生显著影响.对于滑移转向车辆来说,快速通过弯道是为了保证车辆的转向灵敏性和车辆行驶稳定性,这比减少轮胎损耗更为重要.但是现有的研究大多集中于单个轮胎上,例如,在曲线场景中,即使使用相同的轮胎,左侧车轮在潜力和对整体横摆力矩的贡献方面与右侧车轮有明显的差异.同样,前轮和后轮在产生横摆力矩方面也有不同的效率.
针对上述问题,笔者提出一种针对6轮滑移转向车辆驱动力分层控制策略,建立基于滑移转向车辆系统动力学模型、轮胎动力学模型和车轮动力学模型的9自由度动力学模型.基于分层控制思想,上层控制器使用自适应模糊滑模控制得到滑移转向车辆满足转向控制所需附加横摆力矩.通过自适应律逼近法解决滑移转向车辆系统的不确定性和外部扰动等非线性干扰.在下层控制器中,提出一种基于优化分配的驱动力分配方案,根据轮胎负荷率和加权因子,建立目标函数.最后通过实车试验验证提出的控制策略对滑移转向车辆控制的有效性.
1 车辆动力学模型
由于滑移转向车辆没有车轮转角,横摆角速度的响应是通过改变内外侧车轮的转速而实现转向.2自由度车辆动力学模型[1]只能描述车辆横向运动和横摆运动.这里用该模型计算滑移转向车辆理想横摆率,整车模型方程如下:
(1)
式中:m为车辆质量;vx为车辆纵向速度;
vy为车辆侧向速度;γ为横摆角速度;kxi、kyi分别为第i轴轮胎的纵滑刚度和侧偏刚度,i=1,2,3分别为前、中、后轴;a、b、c分别为前、中、后轴距离质心的距离;I为整车转动惯量;B为车辆轮距;Δvx为车辆左右车轮接地点速度差.
基于阿克曼转向车辆2自由度单轨模型计算得到的稳态横摆角速度增益为
(2)
式中:δ为转向盘转角;L为轴距;K为稳定性系数.
与式(2)类比可得,滑移转向6轮车辆稳态横摆角速度增益为
(3)
式中:γd为推导的期望横摆角速度;D/C表征滑移转向6轮车辆的稳定性因数[9];
(4)
期望横摆角速度的选取还需考虑路面附着条件限制,即
γmax=gμ/vx,
(5)
式中:γmax为最大横摆角速度;g为重力加速度;μ为路面附着系数.
对车轮施加纵向力时,由于车轮摩擦椭圆的限制,轮胎横向力的饱和水平会降低,进而出现某个轴可能会先于另一轴饱和.根据文献[6]可知,当后轴车轮率先饱和时,车辆会出现过度转向,严重造成车辆甩尾.定义后轴利用附着系数为
(6)
式中:Fzr为车辆后轴垂向力;Fxr为车轮后轴纵向力.
故可得到6轮滑移转向车辆期望横摆角速度γdes应满足:
(7)
2 滑移转向控制系统设计
滑移转向控制逻辑如图1所示.采用基于分层控制思想,上层控制器根据滑移转向车辆2自由度模型得到车辆期望横摆角速度,耦合轮胎力参考文献[6]进行估算.使用自适应模糊滑模控制实现滑移转向车辆转向控制,在下层控制器中,提出了一种基于优化分配的驱动力分配方案,将决策的横摆力矩分配给各个车轮.
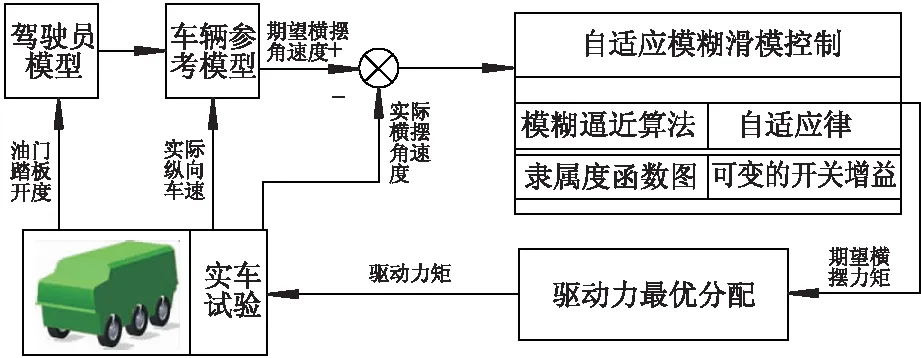
图1 滑移转向控制逻辑图
滑移转向车辆是一个具有强耦合性、不确定性和高非线性的系统,车辆在行驶中,其轮胎侧偏刚度等可能会在各种驾驶条件下发生变化.滑模控制方法由于其对传感器噪声和车辆高非线性系统具有高鲁棒性,被广泛应用于车辆直接横摆力矩控制器中以调节车辆稳定性.本研究利用滑模控制方法设计直接横摆力矩控制器,通过左右车轮形成力矩差控制滑移转向车辆转向跟踪能力和行驶稳定性.
2.1 直接横摆力矩控制器设计
以滑移转向车辆横摆角速度作为控制目标,选取滑模控制作为主要控制方法,滑模面设计和趋近律的选择如下:
s=ε(γ-γdes),
(8)
式中:s为滑模面切换函数;ε为系统状态调节量.
对式(8)两边微分可得
(9)
趋近律设置为
(10)
式中:k、bs为常数,是趋近律调节参数.
控制律为

(Fylm+Fyrm)b+(Fylr+Fyrr)(b+c),
(11)
式中:Fyij为滑移转向车辆各车轮侧向力,ij分别为左前(lf)、右前(rf)、左中(lm)、右中(rm)、左后(lr)、右后(rr)的车轮.
稳定性证明如下:考虑的Lyapunov函数为
(12)
通过对其求导可得
(13)
根据上述控制律,符号函数的存在可以有效消除未知干扰项,但不可避免地导致系统抖振.针对该问题,采用模糊逼近算法构造连续的离散符号函数,从而在根本上减小抖振现象.模糊逼近的设计过程如下所述.
间或读到给仆人的信,我常被大众语言、大众灵魂、大众生活和世界观的绚丽多彩所震撼。 我不由得在心里感叹:“这就是文学啊,最美的文学。”[3]215-216
采用乘积推理机、单值模糊度和中心平均模糊度结算器.模糊系统的输出为
(14)

(15)
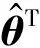
(16)
(17)
式中:r为常数矩阵,根据系统状态设计.
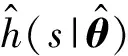
(18)
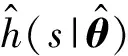
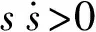

图2 输入隶属度函数
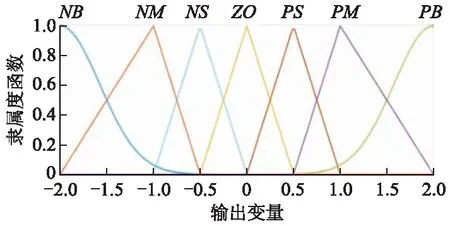
图3 输出隶属度函数
2.2 驱动力最优分配
下层驱动力分配控制器将上层决策得到的附加横摆力矩,对各车轮的纵向力进行再分配,分配的同时考虑路面附着系数的影响,保证车辆转向行驶的稳定性.根据车辆动力学模型得到如下关系:
(19)
式中:Fxij为各车轮纵向力;dw为轴距.
可将式(19)写为矩阵形式:
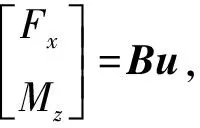
(20)
式中:

方程(19)采用二次规划法求解,基于二次规划理论,首先确定最优目标函数和约束条件.选取车轮纵向力Fxij平方除以垂直载荷Fzij与摩擦系数乘积的平方作为优化目标函数,用于表征车轮的稳定裕度.一般情况下,当目标函数值接近1时,轮胎利用率高,车辆的稳定裕度越低,轮胎与路面的附着力更接近极限,此时车辆处于失稳的临界状态.所以本研究的优化目标是使目标函数值最小化,保证车辆稳定裕度最大化.目标函数可表示为
(21)
式中:J1为稳定裕度函数;Cij为权重因子.
在不同的路面条件下,纵向力也受到路面附着系数和电动机输出转矩的限制.每个车轮的纵向力应满足约束条件:
(22)
式中:Timax为轮毂电动机最大转矩.
将式(19)和(22)改写为
(23)
式中:J2为优化目标函数;W为实对称矩阵;u为纵向驱动力矩阵;umin为纵向驱动力最小值矩阵;umax为纵向驱动力最大值矩阵.
将等式约束转化为min‖Bu-V‖的形式,并将问题转化为序列最小二乘问题,有
(24)
式中:Ww为分配需求w的权重矩阵.
引入权重系数,将最小二乘问题序列转化为加权最小二乘问题,有
(25)
(26)
式中:J为最优函数;Wu为控制变量u的权重系数;κ为权重系数,调节稳定裕度函数与优化函数的权重值.
采用主动集方法求解该方程,得到6轮驱动电动车辆的转矩分配最佳结果.
3 实车试验分析
为了验证本研究提出的针对滑移转向车辆驱动力控制策略有效性,采用课题组研发的6轮毂电动机驱动滑移转向车辆进行转向控制策略实车验证.车辆参数如下:整车质量为1 800 kg,轴距为2 040 mm,前轴距质心距离为960 mm,中轴距质心距离为60 mm,后轴距质心距离为1 080 mm,车轮半径为373 mm,轮毂电动机最大功率为36.4 kW,轮毂电动机最大输出转矩为230 N·m.
由于滑移转向车辆试验平台仍处于研发阶段,整体完成度未达到最优,可靠性仍有不足,6轮毂电动机驱动滑移转向车辆平台如图4所示,其中:GPS(global positioning system)为全球定位系统;VCU(vehicle control unit)为整车控制器.同时受限于试验场地及驾驶员安全性考虑,实车试验主要进行绕S形曲线试验和稳态圆周试验.

图4 6轮毂电动机驱动滑移转向车辆平台
3.1 绕S形道路工况
滑移转向车辆在干燥平整的沥青路面上绕S形曲线行驶实车试验如图5所示.参照GB/T 6323—2014《汽车操纵稳定性试验方法》进行试验,驾驶员操纵转向盘,使汽车以15 km/h左右的车速沿S形曲线行驶.

图5 绕S形道路行驶实车试验
为了定量评价控制算法对滑移转向车辆在鲁棒性及消除抖振方面的控制性能,使用均方根误差eRMS来评价提出的自适应模糊滑模控制策略与传统滑模控制策略的性能.定义均方根误差为
(27)
式中:N为采样次数.
由实车试验可得车辆绕S形曲线行驶的转向试验曲线如图6所示.
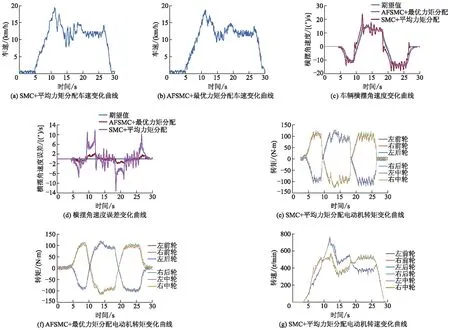
图6 车辆绕S形曲线行驶的转向试验曲线
从图6可以看出:本研究提出的自适应模糊滑模控制(adaptive fuzzy sliding mode control,AFSMC)策略可以控制横摆角速度更好地接近滑移转向车辆的期望横摆角速度,最大偏离期望横摆角速度在2.0(°)/s以内,控制鲁棒性强,而传统的滑模控制(sliding mode control,SMC)策略则使车辆横摆角速度发生较大突变,横摆角速度最大偏离期望值达到12.3(°)/s,车辆转向行驶时出现车辆频繁抖动,横摆角速度短时间内变化量达到15.0(°)/s.从图6e可以看出:SMC+平均力矩分配在到达滑模面前对干扰比较敏感,在车辆转弯时会引起较大的瞬时突变,滑模控制方法会产生明显的抖振,决策的附加横摆力矩分配到各个车轮,使得各车轮转矩发生频繁突变,转矩频繁变化量达到55 N·m,车轮转速进而发生急剧变化.车轮转矩抖动的突然变化不仅影响车辆的乘坐舒适性,还会对电动机和其他部件造成严重损坏,从而大大缩短其寿命.
AFSMC+最优力矩分配方法在有限时间内只发生小的抖振,与传统滑模控制相比,抖振的幅值和频率都大大降低.在横摆角速度方面,AFSMC+最优力矩分配方法比传统的SMC+平均力矩分配方法控制效果更好,使得车辆横摆角速度随动响应更快,滑移转向车辆横摆角速度可以更好地跟踪期望横摆角速度.对比AFSMC+最优力矩分配方法与SMC+平均力矩分配法车辆横摆角速度均方根误差,AFSMC+最优力矩分配方法的均方根误差为0.803,而SMC+平均力矩分配方法的均方根误差达到了3.372,系统抖振频繁.AFSMC+最优力矩分配方法可以在整个过程中将横摆角速度控制在很小的范围内,这不仅保证车辆行驶的完全性、车辆转向性能,而且提高了乘坐舒适性,减小由于频繁抖振对车辆执行器等部件的损坏.
3.2 稳态圆周工况
车辆以13 km/h左右的车速在干燥平整的沥青路面上进行稳态圆周试验.轮毂电动机驱动滑移转向车辆的稳态圆周工况试验曲线如图7所示.
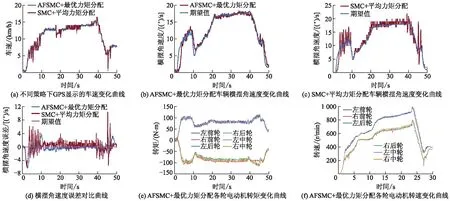
图7 稳态圆周工况试验
从图7a-d可以看出:AFSMC+最优力矩分配方法车辆的车速变化更小,横摆角速度可以更好地跟踪期望横摆角速度,跟踪误差在1.0(°)/s以内,车辆行驶较为稳定,控制器具有较强鲁棒性;SMC+平均力矩分配方法由于抖振的原因,车辆在进行稳态转向时始终处于频繁调节状态,横摆角速度误差大于4.0(°)/s占整个过程的90%,车辆不能很好跟随期望行驶轨迹,乘坐舒适性差;AFSMC+最优力矩分配方法的横摆角速度均方根误差为0.852,而SMC+平均力矩分配法的横摆角速度均方根误差为1.787.从图7e、f可以看出:在AFSMC+平均力矩分配方法和下层最优力矩分配下,滑移转向车辆在进行稳态转向时,轮毂电动机力矩输出稳定,左、右侧电动机转速差几乎恒定,滑移转向车辆可正确跟随期望路径,控制器有效性好.
4 结 论
1)提出了针对滑移转向车辆的自适应模糊滑模直接横摆力矩控制策略,通过实车绕S形道路工况、稳态圆周工况行驶试验,验证了策略的有效性.控制器可以很好解决传统滑模控制由于频繁抖振导致控制变量的突变幅度大、无法快速回复正常的问题,提高了控制策略的鲁棒性并抑制输出控制量的抖振问题.

