嵌岩桩水平承载力计算方法的分析比较
赵学亮, 张景斐, 黄 钺, 何润财, 王洪庆, 田伟辉
(1.东南大学 混凝土及预应力混凝土结构教育部重点实验室, 江苏 南京 211189; 2.东南大学 土木工程学院, 江苏 南京 211189; 3.中国能源建设集团 广东省电力设计研究院有限公司, 广东 广州 510663; 4.中国电建集团 西北勘测设计研究院有限公司, 陕西 西安 710065)
桩基础是一种古老而传统的基础形式,可以充分发挥深层地基土的承载潜力[1],凭借其承载力高、沉降少、适应性强、抗震能力强、施工方便等特点得到广泛的应用.随着跨海大桥、码头、海洋平台等海上结构不断兴建,波浪荷载、风荷载等水平荷载成为这些结构主要承受的荷载,这对桩基础的水平承载能力提出了更高的要求.加上施工技术的发展,大直径灌注桩、钢套管桩等本身抗弯刚度和水平承载能力较大的桩基础出现,水平承载的竖直桩也越来越常见[2].而在基岩浅埋区,如福建、广东等地区,由于地质条件的限制及荷载条件和承载力要求,嵌岩桩日益成为一种经济合理的桩型.
为确定嵌岩桩的水平承载能力,近几年国内外的研究人员进行了许多有益的研究,包括嵌岩桩承受水平荷载时,竖向荷载对位移、桩-土(岩)相互作用的p-y曲线等的影响[3].计算方法上,目前桩基水平承载力的计算方法主要有地基反力法和弹性连续体法等.此外,研究人员还基于国内外相关规范给出的p-y曲线,通过现场试验、温克尔弹性地基梁模型及切线模量、三轴CU试验等方法修正其p-y曲线参数,为承载力的计算提供了参考[4].许多学者依据这些传统桩基的设计方法,基于理论与试验研究结果,提出了嵌岩桩水平承载能力的分析计算方法.但由于岩体材料相对土体具有更强的连续性,材料刚度和强度差异较大,具有风化节理等土体不具备的特性.因此,直接使用普通桩的计算方法是否准确仍有待验证,即使套用相同的计算方法,在参数的选取和计算上也会有较大差距.目前,国内外对承受水平荷载的嵌岩桩的研究仍然不足,各国相关规范中也通常规定需要通过水平静载试验来确定嵌岩桩的水平承载力,实际工程中也常常需要结合现场桩基试验以及数值模拟结果来设计嵌岩桩.
为此,笔者主要对现有计算方法进行比较分析,研究其适用性与局限性,以对嵌岩桩水平承载力设计进行探讨.
1 现有嵌岩桩水平承载力计算方法
1.1 地基反力法
地基反力法类似弹性地基梁法,将桩基看作梁,根据梁的计算理论来计算桩基,推导出桩的挠曲微分方程为
(1)
式中:z为假定桩周土体中任意深度;y为挠度;p为深度z处桩周土体的反力,是深度z和挠度y的函数;EI为桩截面抗弯刚度,大小不变,其中E为桩弹性模量,I为桩截面惯性矩.根据地基反力p的不同确定方式,地基反力法可分为极限地基反力法、弹性地基反力法和p-y曲线法等.
1.1.1极限地基反力法
依据极限地基反力法,假设相较地基刚度,桩基础刚度值很大,极限状态下桩几乎只发生整体的刚体转动,桩基础的失效由地基岩土体的承载力控制,且在桩长范围内的岩土体整体发生屈服.于是先假定处于极限状态时地基岩土体反力的分布形式,再由桩的静力平衡条件求得桩侧岩土抗力的具体数值.
计算嵌岩桩的水平承载力时,也可假定桩在岩面处与岩石完全固接,上覆土中的桩段参数按照地基反力法进行计算,最终确定嵌岩桩的水平承载力.为了满足桩基嵌岩段的嵌固要求,确保岩石不发生破坏,桩身嵌入岩石中的长度也需要满足一定的要求.目前JTG 3363—2019《公路桥涵地基与基础设计规范》、JTS 167—2018《码头结构设计规范》等行业规范以及一些相关研究中计算嵌岩长度的方法也都是假设嵌岩桩为刚体,先假定桩基嵌岩段地层的应力分布情况,再计算需要满足的最小嵌岩深度,因此这些计算方法本质上也属于极限地基反力法.
有学者采用其他假定或方法来计算嵌岩深度.文献[5]对浑河大桥桩基础进行了有限元模拟,与现场试验结果对比,研究结果表明有限元模拟结果与实际情况相吻合,并进一步探讨了嵌岩桩的水平承载特性,认为3倍桩径为最佳嵌岩长度.也有学者认为,对不同层面倾角下层状岩体嵌岩桩的嵌岩深度计算精度的要求应该更高.文献[6]通过数值分析及模型试验,确定了桩径为D的嵌岩桩在完整基岩、基岩层面倾角为0°、30°、-30°、60°、-60°、90°和-90°场地所对应的嵌岩深度分别为2D、3D、3D、4D、4D、4D和3D.
1.1.2弹性地基反力法
弹性地基反力法以温克勒地基模型为基础,将地基岩土体离散成相互独立的弹簧.假定地基岩土体某点反力只与该点水平位移有关,与其他位置的位移无关,不考虑桩土之间的黏着力和摩阻力.地基的各种重要性质主要通过地基系数k(z)这一参数来反映.
由弹性地基反力法可知,任意深度地基反力与该处水平位移成线性关系.根据地基反力系数随深度分布的不同而变化的假设,弹性地基反力法可分为单一参数法和双参数法.单一参数法中,一般取深度的指数函数中指数n为常数,然后根据实际工程情况确定地基系数.双参数法中,地基系数和指数n都需要根据实际情况来确定.单一参数法主要包括张有龄法、Matlock法(m法)、桩基C值法和K法等.JTG 3363—2019中关于桩基嵌岩段设计的规定认为岩石地基系数随深度变化不大,且嵌岩桩嵌入岩石的部分较短,因而采用张有龄法.在我国工程建设中,计算土中水平承载桩的承载力时应用最多的方法为m法.此外,我国部分地方规范,如DBJ 15-31—2016《建筑地基基础设计规范》中提到,当作用在桩基上的力主要为水平力,且桩侧为岩石时,可以采用K法来计算,即在第一弹性零点以上取n=2,在第一弹性零点以下则取k(z)为常数.
双参数法中,反力的表达式有两个可变参数.与单一参数法中深度的指数函数中指数为恒定数值不同,双参数法中深度的指数函数中指数需要根据试验桩的试验测试结果进行调整.但该方法假定岩石处于连续弹性状态,在高荷载水平作用下高估了桩基础的刚度和地基的极限承载力,因此也不适合应用于水平荷载较大或岩石较为软弱嵌岩桩条件下的参数计算.
1.1.3p-y曲线法
在土体的应力与应变均较小的条件下,二者表现出一定的非线性关系,因此单一参数的弹性地基反力法实际上并不适用于计算土体的实际受力情况.为了更好地考虑桩基的非线性受力特性,目前非线性的p-y曲线法已成为国内外岩土工程中应用最多的方法.而软弱岩石的受力也具有较强的非线性特性,因此也有学者参考土体中的p-y曲线法,提出了嵌岩桩的p-y曲线法.文献[7]基于两个预制桩进行试验研究,提出了软弱岩石中桩基的p-y曲线(Reese法)公式,即
(2)
式中:参数yrm=krmD,D为桩径,krm为确定p-y曲线总刚度的量纲一的系数,取值为 5×10-5~5×10-4;Eir为p-y曲线的初始模量,即为曲线的斜率,主要考虑了岩石弹性模量的影响,以及浅层岩石变形后表面出现的裂缝对刚度的影响;yA为线性段与非线性段的分界点与初始位置的距离,可由函数连续性条件确定;pu为单位桩长的桩侧地基岩石极限强度,计算公式如下:
(3)
式中:xr为嵌入岩土中桩身上的某一点距基岩顶面的深度;qu为岩石抗压强度;αr为强度折减系数,反映岩石变形后表面出现裂缝对强度的影响,与岩石质量参数(rock quality designation)drq成线性关系.drq=100时,αr=1/3;drq=0时,αr=0.
在考虑砂土中的水平承载桩时,许多学者常常采用双曲线型的p-y曲线,即
(4)
式中:Ki为初始刚度.
部分学者将这一双曲线型的p-y曲线引入到桩基嵌岩段的计算.文献[8]采用双曲线型的p-y曲线,参考了其他研究者的计算方法,计算了p-y曲线中的Ki和pu,并通过风化岩石中小直径嵌岩桩现场试验的数据,验证了参数选取与p-y曲线的正确性.文献[9]计算地基的极限强度时,考虑了桩前反力与桩侧摩阻力叠加;计算桩侧岩体的剪应力最大值时,则考虑其与粗糙程度、岩石抗压强度的经验关系.文献[10]计算桩前岩石最大压应力时,采用能够考虑岩石风化与完整特性的Hoek-Brown破坏准则,并假定最大主应力为最大压应力,最小主应力为上覆岩层压力,忽略中间主应力.
初始刚度Ki采用文献[8]提出的方法进行计算:
(5)
式中:Em为岩石弹性模量;ν为岩石泊松比;d0为旋转点深度;IT为经验系数.岩石弹性模量应通过试验确定.在没有相关试验数据的情况下,岩石弹性模量可根据文献[11]提出的经验公式进行计算.应注意文献[11]提出的经验公式中无侧限抗压强度单位为MPa,而计算得到的岩石弹性模量Em单位为GPa.
文献[12-13]也基于双曲线模型进行了有限元分析,提出初始刚度Ki和单位桩长的桩侧地基岩石极限强度pu的新求解方法,最后通过多处试验桩的试验数据验证了他们提出的p-y曲线模型.
文献[13]认为深层岩石由于上覆压力较大,不太可能发生楔形的破坏模式.根据对试验桩的有限元分析,假定桩侧应力均匀分布,并考虑了主动土压力pa,最终提出桩侧岩石极限强度表达式为
(6)
式中:pL为岩体抗压强度;τmax为最大水平侧向剪切阻力.
在计算p-y曲线初始刚度时,文献[13]认为文献[7]提出的方法未考虑桩基与岩石相对刚度和泊松比的影响,因此他们基于有限元分析,确定了初始刚度与桩土相对刚度、泊松比、岩石弹性模量的回归关系,用于初始刚度的计算,即
(7)
式中:Dref为参考桩径,取值为0.305 m.文献[13]根据试验数据拟合得到下式,用以计算岩石的弹性模量,即
(8)
式中:Ei为完整岩石弹性模量;IGS为地质强度参数(geological strength index).
文献[13]也提出该方法主要适用于各向同性岩石的参数计算,而不适用于仅由一个节理系控制破坏效应的岩石.文献[14]基于双曲线型的p-y模型,对多组嵌岩桩现场试验数据进行分析,认为p-y曲线初始斜率与地基反力模量、桩长、岩体评价指标值VRQD的乘积之间呈线性关系,并结合现场试验数据,对岩石极限承载力的计算方法进行了修正.
1.2 弹性连续体法
弹性连续体法中,假设桩被埋置于连续、均质、各向同性的半无限弹性土体中,弹性模量及泊松比随深度发生一定规律的变化.该方法考虑了桩土间出现脱离和土体局部出现屈服的情况,但是无法计算桩在地面下的位移、转角及土压力等参数,土体的弹性模量也较难确定.弹性连续体法也被应用于嵌岩桩水平承载力分析中,即进行参数计算时,将岩石及上覆土体都视为连续体,并假设土体及岩石在桩端处深度之上部分的变形模量随深度呈线性增加的趋势,岩石在桩端处深度之下部分的变形模量是不变的.
为了考虑地基进入屈服状态的情况,有学者研究出新的弹性连续体法进行求解[9].求解时,先假设土体和岩石处于线弹性状态,计算土反力随深度变化的分布规律,确定反力超过极限强度后进入屈服状态的土体或岩石的深度范围.将这部分进入屈服状态的土体或岩石提供的反力重新设定其大小等于土体或岩石极限强度,再重新计算反力分布情况.重复上述步骤,直到塑性区不再向下拓展,即可求得最终的反力分布情况.该方法克服了以前弹性连续体法只考虑单层土体及只能用于小位移弹性状态的缺点.近年来,弹性连续体法得到了进一步的拓展,使得该方法适用于大变形、桩基截面和刚度变化、成层土体等情况,并考虑了桩本身产生裂缝后对刚度的影响[15].
2 现有计算方法的比较分析
2.1 现场试验介绍
为了对现有的嵌岩桩水平承载力计算方法进行对比分析,笔者采用文献[12]在美国俄亥俄州进行的一个现场水平承载试验桩试验.通过不同理论计算结果与实测结果的对比,分析不同理论计算方法的准确性.文献[12]进行了试验桩水平加载试验.试验中,开挖到基岩顶面时,将桩基整体嵌入基岩中.根据地质勘察结果,基岩中以软质到中等强度的灰页岩为主.灰页岩为薄层结构,其风化达到轻度风化和破碎程度,有些甚至达到十分破碎的程度.对钻孔采集的页岩岩样进行了直剪试验.根据试验结果,其残余摩擦角为24°,无侧限抗压强度为39.08 MPa.根据岩石强度等级、质量等级及节理的发展程度等,按照文献[16]提出的岩石分级表格进行分级,可以确定岩体质量分级(rock mass rating)RRM如表1所示.进而设置地下水等级为15级,并通过经验公式(9)计算得到地质强度参数IGS,即

表1 不同岩石深度下基岩的RRM和IGS计算结果
IGS=RRM,89-5.
(9)
式中:RRM,89为Z.T.Bieniawski于1989年提出来的岩体质量分级概念[16].
Dayton桩基加载试验布置示意图[12]如图1所示.试验桩(4号桩)和反力桩(3号桩)均为直径为1.83 m的预制钢筋混凝土桩,桩身长度为5.48 m,试验桩与反力桩轴线间的距离为5.48 m,混凝土28 d的抗压强度为31.00 MPa.施加荷载时按222.4 kN或444.8 kN的荷载增量逐级进行加载,最大施加荷载为5 008.7 kN,最后进行卸载.
2.2 对比验证结果
笔者使用用于单桩水平荷载设计计算的软件——Lpile软件,对采用常数法、m法、文献[7]提出的p-y曲线法(Reese法)和文献[13]提出的p-y曲线法(Liang法)计算得出的嵌岩桩水平承载力结果进行对比分析,并与上述现场试验测试结果进行对比.Lpile软件是目前美国工程界广泛应用的水平受荷基桩分析软件,该软件可以对桩基在轴向和水平荷载、土体位移作用下的位移控制方程进行求解,并能计算裂缝发展对桩身刚度的影响,且内置了有关现有砂土、黏土和岩体的p-y曲线,也能接受用户自定义的p-y曲线.
由于JTG 3363—2019中并未规定岩石地基中地基反力比例系数m值的计算方法或取值范围,因此此处采用m法是按照现场试验荷载-位移曲线来调整m值,使其计算得到的荷载-位移曲线相对接近于现场试验结果,因此取值m=5.09×105kN/m4.常数法中的地基反力比例系数C的取值除了根据JTG 3363—2019要求,依据岩石单轴抗压强度取值C1=1.50×107kN/m3作为常数法的第1种算法外,也参照上述m法的处理方法,根据现场试验数据调整C值,最终取值C2=5.08×105kN/m3,作为常数法的第2种算法.
采用基于Lpile软件的不同理论计算方法和试验实测方法得到的嵌岩桩桩顶水平荷载ph与水平位移Sh,t的关系曲线,如图2所示.
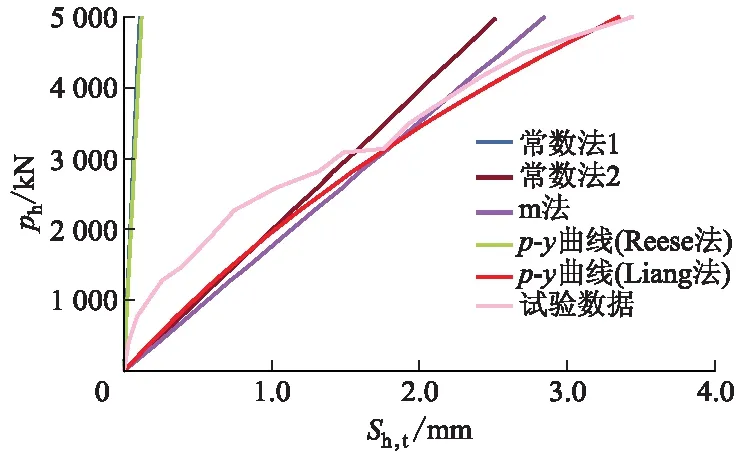
图2 不同计算方法与试验实测得到的桩顶荷载-位移曲线
由图2可知:Reese法与试验实测的结果差距较大,这是因为该方法远远低估了嵌岩桩的位移,Liang法则与实测结果较为接近;如果m法和常数法中的地基反力比例系数选取合适,那么计算得到的荷载-位移曲线会与试验结果较为接近(见常数法2曲线);如果根据JTG 3363—2019要求取C值,常数法计算结果将与实测结果差距很大(见图2中常数法1的曲线).若要使荷载-位移曲线接近实测曲线,C值大致需减少到JTG 3363—2019规定值的1/30,因此JTG 3363—2019中C值的取值方法不符合实际情况.此外,实测的荷载-位移曲线有一定程度的弯曲,而m法和常数法计算得到的荷载-位移曲线近似一条直线.可见即使根据实测结果来调整m值与C值,也无法做到在低荷载和较高荷载情况下同时接近实际情况.而Liang法在一定程度上体现了基础变形的非线性特征,相对于前两种方法更接近实测数据,但在荷载较小时与实测数据仍有一定差别.
不同计算方法与试验实测得到的不同荷载下桩身深度z与水平位移Sh,b关系曲线如图3所示.由图3可知:与桩顶荷载-位移曲线类似,各个方法在荷载较小时计算结果与实测结果均有较大差距;荷载增大后,Liang法、m法和常数法的计算结果逐渐接近实测结果,按JTG 3363—2019计算的常数法以及Reese法仍然与实测结果差距较大;m法计算结果的位移曲线整体变化趋势与实测曲线最为接近;Liang法和常数法计算结果的总体精确度稍差一些,虽然在荷载为5 009 kN时Liang法计算的桩顶附近位移更接近实测结果,但总体上m法计算结果更为准确.

图3 不同计算方法与试验实测得到的桩身深度-位移曲线
图4为不同计算方法与试验实测得到的桩身最大弯矩Mmax与水平荷载ph关系曲线对比.图5为不同计算方法与试验实测得到的桩身弯矩M与桩身深度z关系曲线对比.
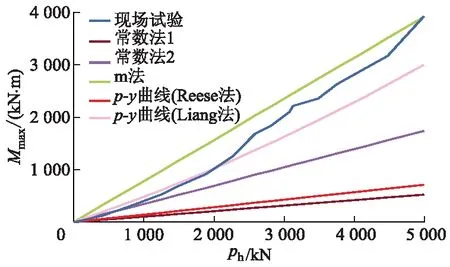
图4 不同计算方法与试验实测得到桩身最大弯矩-荷载曲线

图5 不同计算方法与试验实测得到的桩身弯矩-桩身深度曲线
由图4、5可知:m法与Liang法最大弯矩的计算结果与实测结果较为接近,桩身弯矩随深度的变化趋势和最大弯矩出现的位置也与实测结果较为一致;m法计算得到的弯矩几乎全都大于实测结果,而Liang法计算结果在荷载较小时十分接近实测结果,在荷载较大时则偏小;常数法计算得到的弯矩小于实测结果,如根据JTG 3363—2019规定取C值,弯矩计算结果依然与实测结果差距较大,且最大弯矩出现的位置深度相对较浅,即使调整C值后弯矩计算结果也不如m法与Liang法准确;Reese提出的p-y曲线法计算结果与实测结果差距较大.
综上,Liang提出的p-y曲线与m法的计算结果最接近试验结果,但仍存在不吻合之处,且m法的使用中需要确定较为准确的m值;常数法计算结果的准确度稍差于上述两种方法,且同样需要确定较为准确的C值,JTG 3363—2019规定的取值方法显然无法满足这一要求;Reese提出的p-y曲线法计算结果与实测结果差距较大.
2.3 现有方法的适用范围及局限性
根据对现有嵌岩桩水平承载力计算方法的假设条件和原理的分析,以及与现场原位试验实测数据的对比,可以总结出目前常用的地基反力法和弹性连续体法的适用范围及局限性.
1)地基反力法.该方法的核心问题是确定地基反力p与挠度y的关系,主要根据大量的试验桩试验、工程经验或数值模拟结果来确定二者大致的函数关系,再分析曲线中各参数的影响因素,确定参数的计算方法.该方法经验性较强,但也因此将实际地基和桩基础中的各种复杂情况考虑在内.但地基反力法采用了温克勒弹性地基梁的假设,将岩土体离散成多个独立的弹簧,忽略了岩土体上下层之间的相互约束力,因此未能很好地考虑岩石的连续性.但有学者认为p-y曲线是基于试验桩现场试验数据得到的,所以在其推导和计算中实际上已经考虑了土体之间的相互作用.由于地基反力法具有较强的经验性,某种特定的地基反力法或某一个p-y曲线很可能无法适应所有情况.现有p-y曲线大多是基于国外现场试验桩试验,可能不适用于我国岩土体条件,近几年许多试验结果也表明,将基于小直径桩推导的p-y曲线应用于大直径桩会产生较大的误差.
根据极限地基反力法的假设,该方法主要适用于桩基入土深度和截面尺寸均由水平荷载确定的情况,且其研究对象为相对于地基土刚度较大的刚性短桩,不适用于柔性较大的长桩.JTG 3363—2019规定的嵌岩深度计算方法也是基于极限地基反力法,因此适用于嵌入岩石不是太深的桩基.相比之下,弹性地基反力法可以考虑地基岩土体在不同位置处于不同受力状态,因此同时适用于刚性桩和弹性桩.单一参数法的假设虽然与地基岩土体的实际情况不符,但应用于小变形桩计算中能较为准确地得到桩顶位移、最大弯矩等重要参数,且计算较为简单,使用方便.按照2.2节中的结果,在系数k(z)取值恰当时,单一参数的弹性地基反力法(常数法和m法)应用在嵌岩桩中的计算结果也能够接近实际情况,但目前该方法的应用还存在一定的缺陷.
JTG 3363—2019中对于嵌岩段都采用了常数法的假设,但该方法可能是针对上覆土层较厚、嵌岩深度较浅的嵌岩桩提出的,对于嵌岩深度较深的桩是否成立还需要进一步的验证,并且该规范中C值仅根据岩石单轴抗压强度确定,没有考虑岩石风化、破碎程度及桩基尺寸等因素的影响.由2.2节中的计算结果对比分析可知,该规范规定的常数法参数取值方法高估了岩石地基及嵌岩桩和岩石整体的刚度.m法相比于常数法考虑了岩土体受力性能随深度变化的情况,因而更贴近实际情况,m值一般根据地基土种类及现场试验确定.但在岩石地基中该方法的应用和研究较少,在缺乏现场试验数据的情况下m值也没有明确的确定方法.同时,许多研究也指出,当桩基承受较大的水平荷载、岩土体较为软弱及桩周土体发生较大变形时,岩土体会发生软化,非线性反应更加明显,m法中的系数m值随之减小.依据JTG 3363—2019中规定,计算得到的m值容易产生较大误差.且随着桩的变形量增大,m值的敏感性增大,如何确定合适的m值是一个很重要的问题.对于K法,多处试验桩的计算结果表明,使用该方法计算得到的桩身截面弯矩比实际情况大得多,因此该方法是否能准确计算嵌岩桩的水平承载力还有待进一步的研究.双参数法中由于采用两个待定参数,计算结果更符合实际情况.但针对不同的桩基和地基条件也需要更多原位试验桩数据来确定这两个参数以及桩土(岩)共同工作的综合刚度,因此目前该方法未能得到推广.
近年来p-y曲线法应用较多.该方法能考虑软弱岩石地基的非线性反应,且更细致地考虑了不同因素对地基反应的影响.但嵌岩桩参数计算中,对于p-y曲线选取和参数确定,经常直接套用土体中参数的计算方法,因此其准确性有待更多研究进行验证.如Reese提出的p-y曲线存在过度依赖其采用的两个现场试验数据的问题,且对岩体的破坏模式没有准确定义.许多文献也通过其他现场试验进行验证,指出该方法高估岩石的刚度.在本研究的算例中,Reese法计算结果也验证了这一点.而Liang法虽然大致上与试验结果相符,但也在某些方面存在较大差距.此外,目前仅有文献[17]提出的p-y曲线参数考虑了横观各向同性的岩体.目前还没有较好的方法能考虑到节理分布更加复杂的岩体,因此嵌岩桩中的p-y曲线法仍有待进一步的发展.
2)弹性连续体法.该方法假设地基弹性模量随深度呈线性变化,并基于弹性力学理论,计算桩体在半无限平面土体中的受力情况.还有人研究了地基进入塑性状态后的计算方法,理论概念相对地基反力法更加清晰,考虑了岩石地基连续性,但其计算过程相对复杂,对岩体的脆性破坏、各向异性、大直径桩桩端的嵌固效应等情况尚未很好地考虑.
针对嵌岩桩水平承载力,现有的方法大多缺乏更多试验数据和工程实例的验证,许多文献也指出现有的嵌岩桩水平承载力计算模型适用范围较小,只适用于特定的岩土条件.实际工程中,当上覆土层较厚、嵌岩深度较小时,采用常数法计算或通过控制嵌岩深度也能满足工程设计要求.但当上覆土层较薄、嵌岩深度较深时,就需要根据岩体的完整程度、变形特征等因素选用弹性连续体法、p-y曲线法等更为复杂的计算方法.且由于参数计算对数值分析和试验桩试验过于依赖,因此研究水平承载嵌岩桩计算理论和设计方法时需要考虑岩石风化特性、桩基尺寸等影响因素,并通过大量现场试验数据对现有计算理论和设计方法进行完善.
3 结 论
1)地基反力法经验性较强.其中极限地基反力法只适用于刚性短桩;单一参数的弹性地基反力法计算简便,适用于刚性桩和弹性桩;m法计算结果基本能够符合工程要求,但是当缺乏现场试验数据时,嵌岩桩参数的选取较为困难,计算结果容易产生较大误差.
2)相较单一参数法,双参数法计算结果更加准确,但参数计算需要更多现场试验数据进行支撑,因而适用于重大工程.
3)p-y曲线法考虑了地基的非线性反应,更适合大变形桩,但缺乏更多试验验证.Reese提出的p-y曲线与实际结果差距较大,Liang提出的p-y曲线相对准确.
4)弹性连续体法的参数概念更加清晰,推导过程更加严谨,且考虑了岩石地基的连续性,但对于实际工程中的复杂情况较难考虑.

