乘法噪音下Kuramoto-Sivashinsky方程的后向紧随机奇拉回吸引子①

夏欢， 李扬荣

西南大学 数学与统计学院，重庆 400715

1 带乘法噪音和彩色系数的随机K-S方程

文献[1-2]引入了有周期边界的一维确定型Kuramoto-Sivashinsky(K-S)方程作为反应扩散系统中湍流和波传播的一维模型.文献[3-4]研究了确定型K-S方程.文献[5-9]和文献[10]分别研究了Wiener噪音和Lévy噪音下的随机K-S方程.本文主要研究带有乘法噪音和彩色系数的随机K-S方程

(1)

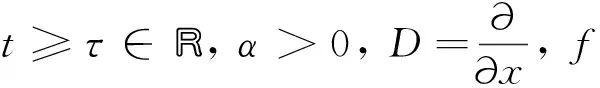
设状态空间为

本文主要研究其对应的奇空间

H0={u∈H:u(t,-x)=-u(t,x)}

上的后向紧拉回随机吸引子的存在性.勒贝格空间H0被赋予通常的L2范数

令(Ω,F,P)为标准的Wiener空间,其中

对于非自治动力系统(1),为了研究其长时间动力行为,我们关注其生成的拉回随机吸引子A(τ,ω)(见文献[12,15]). 由于在H0或V0上,方程(1)的解满足u(t,-x)=-u(t,x),因此A(τ,ω)由奇函数组成,这样的吸引子被称为奇吸引子.在本节,我们取集族B由H0中所有后向缓增的双参数集B构成,其中B为

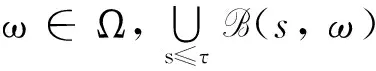
我们考虑如下的变量变换:

v(t,τ,ω,vτ(x))=e-αz(θtω)u(t,τ,ω,uτ(x))-ξ(x)

(2)

(3)

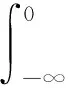
(4)

(5)

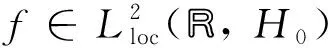
Φ(t,τ,ω,uτ)=u(t+τ,τ,θ-τω,uτ)=eαz(θtω)(v(t+τ,τ,θ-τω,vτ)+ξ)

(6)

其中初值uτ=eαz(ω)(vτ+ξ(x)).Φ关于t,τ,uτ是三元连续的,且关于ω∈Ω是可测的.

2 解的后向一致估计

为了得到K-S方程(5)的解的后向一致估计,我们给出外力项f(t,x)和噪音系数α的一些合理假设.

假设1存在某个常数c0<+∞,使得噪音系数0<α≤c0.

事实上,α可以看作一个控制方程(1)中噪音项增长速度的常数.若没有特殊说明,c为任意常数.

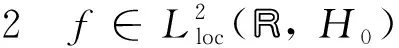
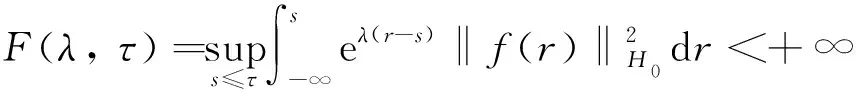
显然F(λ,·)是增函数.若f后向缓增,则f是缓增的,且

引理2若假设1、假设2成立,则对任意的τ∈R,ω∈Ω和B={B(τ,ω)}∈B,存在T=T(B,τ,ω),使得

(7)

对所有t≥T,us-t∈B(s-t,θ-tω)一致成立.其中

(8)

(9)

证在方程(5)两端同时乘2v(r,s-t,θ-sω,vs-t),并关于x∈G积分,有

(10)

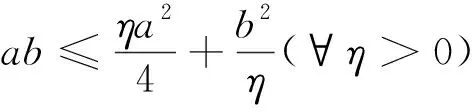
再由分部积分法,有2(ξDv,v)=-(vDξ,v),于是2(D(ξv),v)=(vDξ,v).下面由假设1和ξ的连续性对(10)式的右边项进行估计:

2(αz(θr-sω)ξ,v)≤c|z(θr-sω)|2+‖v‖2

-2(ηD4ξ+D2ξ+ξDξ,v)≤c+‖v‖2

则(10)式可放缩为

(11)

(12)

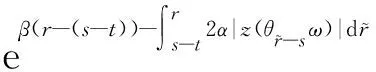
(13)

通过变换u(s)=u(s,s-t,θ-sω,us-t)=eαz(ω)(v(s,s-t,θ-sω,vs-t)+ξ),并借助(a+b)2≤2a2+2b2,有

(14)

其中‖vs-t‖2≤ce-2αz(θ-tω)‖us-t‖2+c,If为f的相关项,I1为f的无关项.

由(4)式,存在某个T0=T0(ω)>0,使得对任意t≥T0,有

于是

(15)

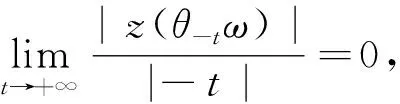
(16)

(17)

最后证明If可由变量R1(τ,ω)控制.为了统一,我们仍对时间s≤τ取上确界

(18)

综合(17)和(18)式即证得解u(t,τ,ω,uτ)的后向一致估计(7)式.

推论1根据(13)和(14)式,对任意ω∈Ω,τ∈R,有

(19)

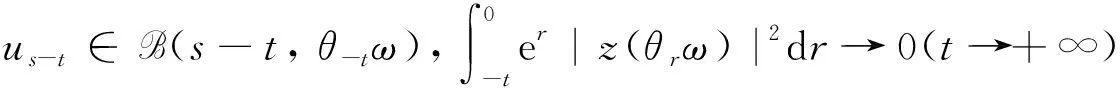
我们可以得到

(20)

命题1协循环Φ有一个B-拉回吸收集K,由如下形式给定:

(21)

其中R0(ω),R1(τ,ω)分别由(8)和(9)式给出.并且K={K(τ,ω)}∈B是一个后向吸收集,即对任意B∈B,τ∈R,ω∈Ω,存在T=T(τ,ω,B),使得对于任意t≥T,有

(22)

证首先证明K={K(τ,ω)}∈B.由于z(θtω)是随机变量,则R0(ω)是随机变量.由(15)式,对每个ω∈Ω,有R0(ω)<+∞成立.另外,由于R0(ω)与变量τ无关,因此只需证R0(ω)是缓增的.

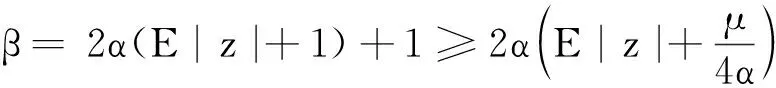
(23)

由(4)式有

因此

(24)

(25)

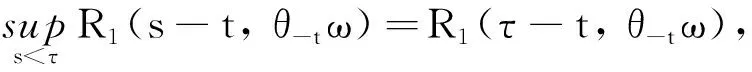
(26)

由(26)式即证R1(τ,ω)是后向缓增的.最后由引理2,对任意t≥T=max{T0,T1},有

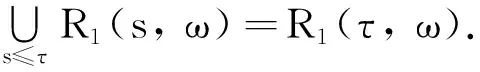
为了得到吸引子,接下来我们对方程(5)在状态空间V0上的解进行后向一致估计.

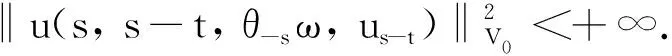
证将方程(5)两端同时与2D4v(r,s-t,θ-sω,vs-t)做内积,

(27)

首先利用Young不等式和Gagliardo-Nirenberg插值不等式对(27)式中的某些项进行估计,

再利用假设1和ξ(x)的连续性对(27)式的剩余项进行估计,

综合上述估计可以得到不等式

(28)

再根据微分形式的Gronwall引理,有

(29)

(30)

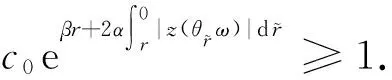
(31)

最后利用(19)式可对(29)式的剩余项进行估计,存在TJ3=TJ3(B,τ,ω),当t≥TJ3时,

(32)

3 后向紧随机奇拉回吸引子的存在性

uk=Φ(tk,sk-tk,θ-tkω,u0,k)=u(sk,sk-tk,θ-skω,u0,k)

(33)

引理3已证{uk:k∈N}在V0中有界,再根据V0紧嵌入H0知{uk:k∈N}在H0中有收敛子列,即序列{uk:k∈N}在H0中是预紧的.

接下来证明后向紧的奇拉回吸引子AB的存在性.在(22)式中取s=τ,于是有Φ(t,τ-t,θ-tω,B(τ-t,θ-tω))⊂K(τ,ω),∀t≥T(B),B∈B,即K(τ,ω) 是吸收集.在(33)式中取sk=τ,则对应的序列{u(τ,τ-tk,θ-τω,u0,k)}有收敛子列,即Φ是后向渐近紧的.因此根据文献[15]的吸引子存在定理可得AB存在,且由ω-极限集构成,

(34)