广义分位数的渐近性质①

杨茜， 彭作祥

西南大学 数学与统计学院，重庆 400715

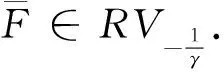
H(0)=0H(1)=1H′+(0)=0

文献[1]定义X的广义分位数

(1)

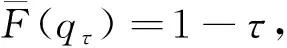
定理2在定理1的条件下,有

在证明定理1之前,先引入3个引理.

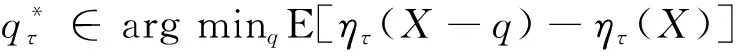
证参见文献[1]引理3.

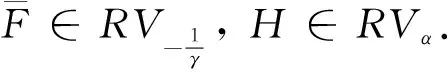
证记

(2)

其中

(3)

由文献[14]的命题0.7(b)可知H′∈RVα-1.根据文献[14]的命题0.5,控制收敛定理及正规变化函数的局部一致收敛性,有

(4)

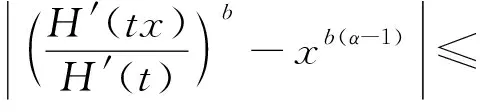
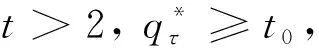
(5)

因此,由(3)-(5)式可得

(6)

对Δ2(τ),同样由文献[15]的定理B.2.18可知,对任意>0,0<δ<γ-1-b(α-1),存在(,δ)使得对有

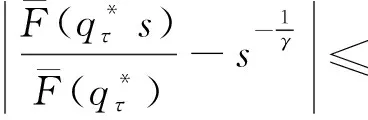
因此,

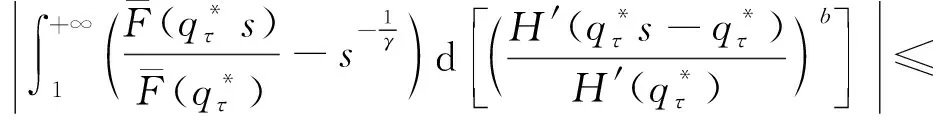
注意到

(7)

由(2),(6)与(7)式可知结论成立,引理证毕.

定理1的证明由引理1可知

等价于

(8)

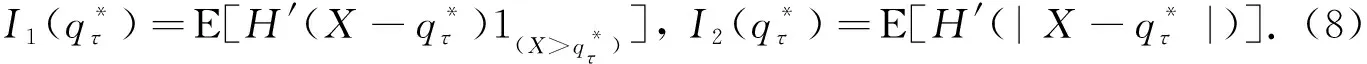
由引理3,令b=1有

(9)

记

对第三项A3(τ),有

(10)

由文献[14]的命题0.7(b)可得H′∈RVα-1,类似引理3的证明有

(11)

(12)

由(10),(11)与(12)式可得A3(τ)收敛到1.因此,

(13)

联合(8),(9)与(13)式可得定理得证.