相依时序逐日盯市条件尾期望的经验估计①

陈皓钰， 彭作祥

西南大学 数学与统计学院，重庆 400715

近年来,风险度量在金融市场中变得愈加重要.记投资组合收益为随机变量X,其累积分布函数为FX(x).给定显著性水平α∈(0,1),在险价值

VaRX(α)=-sup{x:FX(x)≤α}

给出了投资组合以α的概率所遭受的最小损失值.文献[1-2]分别刻画、研究了对冲基金的风险特征与资本充足率,及住宅市场的下行风险.文献[3]将在险价值与医院金融风险管理相结合,以达增强医院资产流动的目的.但VaR因不满足次可加性,故不是一致性风险度量[4].作为本文的研究对象,条件尾期望

CTEX(α)=-E(X|X≤-VaRX(α))

刻画了投资组合在损失超过阈值VaRX(α)时所遭受的期望损失值,且当FX(x)为连续函数时,其满足一致性风险度量的所有理想性质[4-5].关于条件尾期望估计量及条件尾期望在银行、金融服务与保险等领域的广泛应用,见文献[6-12].

尽管在险价值与条件尾期望有着简单且易于理解的表达式,但其是根据持有期结束时的投资组合收益变化计算的.故当金融机构出现投资组合在其持有期内有多次结算时,在险价值与条件尾期望很难适用于该金融机构内部风险的评估.同时为缓解在险价值对资产市场风险的低估,基于投资组合在每一个连续交易日的收益时序{X1,X2,…},文献[13]提出了逐日盯市在险价值

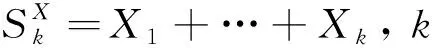
的α分位数.基于逐日盯市在险价值,本文提出逐日盯市条件尾期望:

为保证逐日盯市条件尾期望满足风险度量一致性公理,且为便于后续理论推导,本文针对Y1的累积分布函数FY,作如下假设:

(i)FY在定义域内连续;

(iii)F′Y(ξα)=:f(ξα)>0.

其经验估计量定义为

本文主要结论如下:

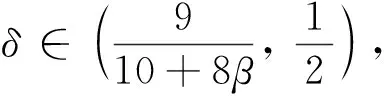
(1)

几乎处处成立.

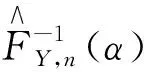
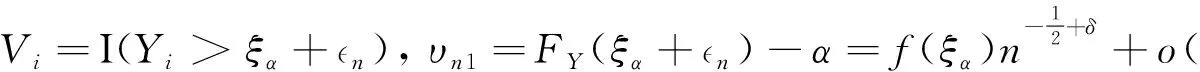
(2)

类似地,有

(3)

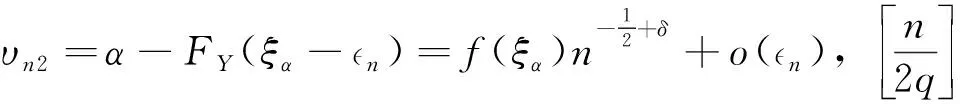
则由Borel-Cantelli引理可知(1)式几乎处处成立.定理证毕.

如下定理2给出了逐日盯市在险价值经验估计量的渐近分布.

记Hn=Y(kn),则

(4)

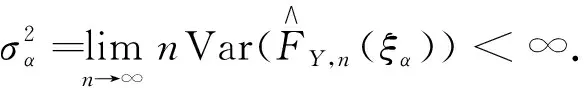
证因为

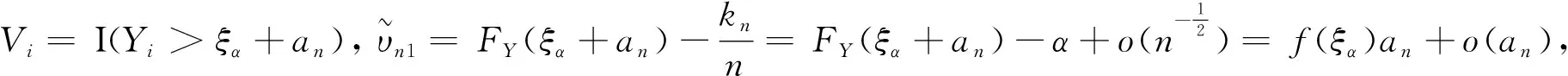
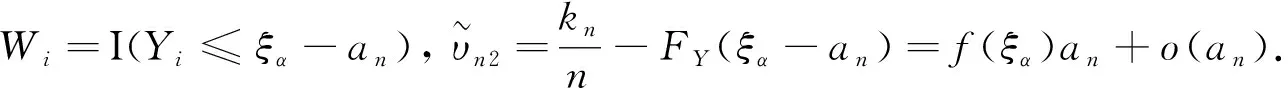
(5)

(6)

(7)

综合(6),(7)式可知(4)式成立.定理证毕.

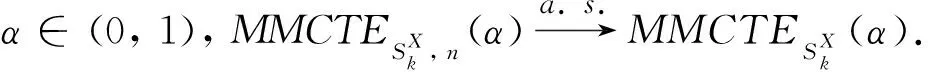
证若证得

(8)

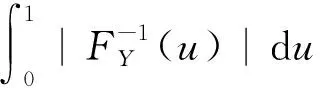
(9)

(8)式的左边部分可拆分为

(10)

(11)

(12)

与

(13)

定理4假设定理1的条件成立,则对任一给定的α∈(0,1),

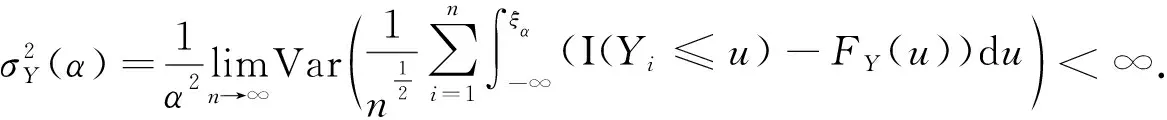
证首先计算如下积分:

(14)

基于类似的计算步骤,可得

(15)

接着计算如下等式:

其中基于(14)与(15)式可得

由此可知RY,n(α)的界为