无界域上非自治Navier-Stokes方程的后向紧动力学
佘连兵,高云龙
(六盘水师范学院 数学与信息工程学院,贵州 六盘水 553004)
Navier-Stokes方程是流体力学中描述粘性牛顿流体的方程, 在流体力学的研究中有十分重要的意义。目前关于Navier-Stokes方程的动力学行为已被广泛研究, 见文献[1-6]。
最近, 文献[7]研究了非紧的非自治动力系统的拉回吸引子A={A(t)}t∈R的后向紧性, 即∪s≤tA(s)是预紧的, 并建立了相应的存在性理论;文献[8]运用能量的方法, 对解进行高低频分解,结合Sobolev嵌入的方法获得具有弱耗散非自治Schrödinger拉回吸引子的后向紧性;文献[9-10]分别研究了非自治Reaction-Diffusion方程在有界域和无界域上的后向紧拉回吸引子的存在性,这些结果体现了非自治动力系统对时间依赖的特点。本文将利用该存在性理论研究如下无界Poincaré型域Q上的非自治Navier-Stokes方程的后向紧动力学:
(1)
其中:t≥τ,τ∈R;常数ν>0是流体的运动粘度;u是流体的速度场,p是流体所受的压力;f(x,t)是流体的外驱动力;无界开集Q⊂R2满足如下的Poincaré不等式:

(2)
在外驱动力f是后向一致缓增有限的假设下(见假设F), 证明了方程(1)在一个能量空间上具有一个增的拉回吸收集。此外, 为了克服无界域没有紧Sobolev嵌入的困难, 本文借助Ball能量方程的方法和一个k-能量不等式证明了系统的后向渐近紧性, 从而证明了非自治Navier-Stokes方程的后向紧吸引子的存在性。
1 Banach空间上的非自治过程的后向紧动力学
本节给出非自治动力系统的一些基本概念(见文献[11])和后向紧拉回吸引子的定义(见文献[7])。设X是一个Banach空间,X中两集合A和B的Hausdorff半距离定义为:
定义1设A={A(t)}t∈R中的一个非自治集, 对任意t1,t2∈R,当t1≤t2时,若A (t1)⊂A (t2), 则称A是增的;若A(t1)⊃A (t2), 则称A是减的。
定义2若定义在Banach空间X上的一族映射S(t,s):X→X, ∀t≥s, 满足对于任意t≥r≥s有S(s,s)=I,S(t,s)=S(t,r)S(r,s), 则称S(·,·)是X上的一个非自治过程。
定义3[7]若X中的一个非自治集A={A (t)}t∈R满足:

②A是不变的, 即对于所有的t≥τ, 有S(t,τ)A(τ)=A(t);
③A是拉回吸引的, 即对于X中所有的有界集B, 有
则称A是一个关于S(·,·)的后向紧拉回吸引子。
定义4设S(·,·)是定义在X上的一个非自治过程, A={A(t)}t∈R是X中的一个非自治集, 若对每一个t∈R和X中的有界集B, 都存在τ0=:τ0(t,B)>0使得
则称K是一个关于S(·,·)的拉回吸收集。

定理1[7]设S(·,·)是定义在Banach空间X上的一个非自治过程, 若满足:
①S(·,·)在X上有一个增的有界的吸收集K={K(t)}t∈R;
②S(·,·)是后向渐近紧的;
则S(·,·)存在唯一的后向紧的拉回吸引子A={A(t)}t∈R, 其中
(3)
2 无界域上非自治Navier-Stokes方程的后向紧动力学
2.1 函数空间与解生成的非自治过程
本文考虑如下的函数空间:
记H为V在L2(Q)×L2(Q)上的闭包, 并对H赋予如下的内积(·,·)与范数‖·‖:

此外, 分别记V*和H*为V和H的对偶空间, 记〈·,·〉为V和V*对偶积, 且嵌入V⊂H≡H*⊂V*是连续的和稠密的。下面在V×V×V上定义一个三线性形式b(·,·,·):
由文献[1-2]可知b(·,·,·)具有如下性质:
b(u,v,v)=0, ∀u,v∈V;
(4)
(5)
u(·,s,u0)∈C(s,T;H)∩L2(s,T;V), ∀T>0;
(6)

(7)
于是方程(1)的解可定义如下的非自治过程S(·,·):H→H:
S(t,t-τ)u0=u(t,t-τ,u0),τ≥0,t∈R。
(8)
2.2 无界域上非自治Navier-Stokes方程增的拉回吸收集
为了获得一个增的拉回吸收集, 对时间依赖的外力项做了一个不同于文献[7]的假设:

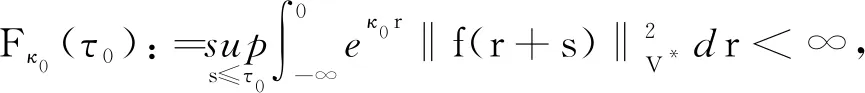
(9)


(10)

于是式(10)成立, 证毕。
引理2若条件F成立,则对每个t∈R和H中的有界集B, 存在τ0:=τ0(t,B)>0,使得
(11)
证明由式(1)、(4)和(7)可得如下能量方程:

(12)
由Poincaré不等式(2)和Young不等式可知:
(13)
对不等式(13)在(s-τ,s-k),s≤t,τ≥k≥0上用Gronwall不等式可知:
当τ→+∞时, 上式右边第一项趋于零,引理得证。
由引理1~2可证明非自治Navier-Stokes方程(1)在H中有一个增的有界的拉回吸收集。

证明显然K(t)关于时间t是增的,故K是增的。由引理1可知K是有界的, 最后由引理2在k=0时可知K是过程S(·,·)的一个拉回吸收集。证毕。
2.3 无界域上非自治Navier-Stokes方程的后向渐近紧性
由文献[2,6]中关于自治方程解的弱-弱连续的结果, 可类似地证明如下结果:
引理4对每一个τ∈R, {u0,n}n∈N⊂H,u0∈H, 若在H中有u0,n⇀u0, 则方程(1)的解
在H中有
v(t,s,u0,n)⇀v(t,s,u0), ∀t≥s,s≤τ;
(14)
在L2(s,T;V)中有
u(·,s,u0,n)⇀u(·,s,u0), ∀T>0。
(15)
由Ball能量方程方法, 可以证明非自治Navier-Stokes方程的解在H中的后向渐近紧性。
引理5若假设F成立, 则非自治过程(8)在H中是后向渐近紧的, 即对每一个t∈R和H中的有界集B, 当sn≤t、τn→+∞、u0,n∈B时有{S(sn,sn-τn)u0,n}={u(sn,sn-τn,u0,n)}在H中有一个收敛子列。
证明由于τn→+∞, 由引理2在k=0时可知存在N0∈N,使得当n≥N0时τn>T, 故

(16)
由式(16)可知
于是,只需证明
(17)
给定k∈N, 容易验证
u(sn,sn-τn,u0,n)=u(sn,sn-k,u(sn-k,sn-τn,u0,n))。
(18)
由引理2可知存在Nk∈N,使得当n≥Nk时有
(19)
故由式(18)~(19)及引理4可知, 在H中
(20)
在L2((sn-k,sn),V)中
(21)
于是由式(16)、(20)可知
(22)
另一方面,由式(12)可得如下能量方程:

(23)
其中φ(u)=2ν‖u‖2-νλ‖u‖2。由式(2)可知φ(·)是V的一个等价范数。再由式(22)、(23)可知
(24)
由式(18)、(23)可知
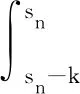

(25)
下面考虑n→∞时式(25)的极限。由引理2在k=0,s=sn,τ=τn时可知
(26)
由u0,n∈B可知
(27)
由式(21)可知

于是,

(28)
再由式(21)可知
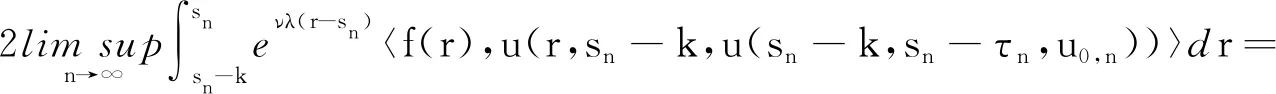
(29)
最后由式(25)、(27)~(29)可知
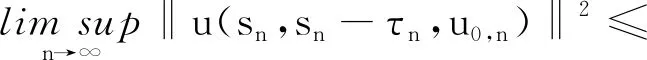
(30)
故由式(24)、(30)可知
令k→∞可得式(17),证毕。
2.4 非自治Navier-Stokes方程后向紧吸引子的存在性
证明了系统增的吸收性和后向渐近紧性后, 可以证明无界域上非自治Navier-Stokes方程后向紧吸引子的存在性。
定理2若假设F成立, 则无界域上非自治Navier-Stokes方程在H上存在唯一的后向紧的拉回吸引子A={A(t)}t∈R, 其中,
(31)
证明由引理2可知式(8)中的非自治过程S(·,·)在H中有一个增的有界的拉回吸收集K={K(t)}t∈R, 再由引理式4可知S(·,·)是后向渐近紧的, 故由定理1可知S(·,·)存在唯一的后向紧的拉回吸引子A={A(t)}t∈R并由式(31)给出,证毕。

