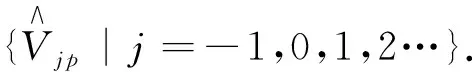B类Kadomtsev-Petviashvili非线性系统的弦方程和Virasoro约束①

倪雨星， 刘少伟

西南大学 数学与统计学院，重庆 400715

B类Kadomtsev-Petviashvili(BKP)系统是一个被广泛研究的受多重约束的非线性KP系统[1],这里的B表示奇维正交群,满足额外(Lp)-=0,p∈Nodd约束的BKP系统形成的p约化BKP系统.其中3约化BKP系统能导出著名的非线性偏微分方程Sawada-Kotera方程[2-3],并被广泛用于共形场理论和二维量子引力规范场理论.弦方程是弦理论中的主要研究对象,也是连接可积层次与可解弦理论和相交理论的重要约束[3],还与一些类KP系统的可积方程密切相关,受到了广泛的关注.在二维量子引力中,文献[4]证明了模空间交集理论的配分函数恰好是弦方程约束KdV系统的τ函数的对数.由于附加对称性的不动点集在KP系统是不变的,所以弦方程对由KdV系统可积方程产生的流是不变的,而弦方程恰好是这种平衡性的条件[5].近年来,众多学者试着把Kontsevich的结论推广到更高维和多约束的情况,而BKP恰好是主要研究对象之一[6-8].文献[9]给出了BKP系统的ASvM公式.文献[10]受KP系统的启发,基于Dickey的方法给出了BKP系统的ASvM公式的另一种证明.文献[11]研究了BKP系统的弦方程以及BW1+∞.文献[3]又从Lax-Orlov-Schulman公式中附加对称性的角度重新考虑BKP系统的弦方程.

然而,通过分析发现文献[3,11]中的弦方程的引入会导致数学上的矛盾,即会使得L-p=0,从而使系统退化成为最平凡的情况,失去研究的意义.因此,本文将在如下p约化BKP系统可积系统里重新探讨BKP系统的弦方程:

(1)

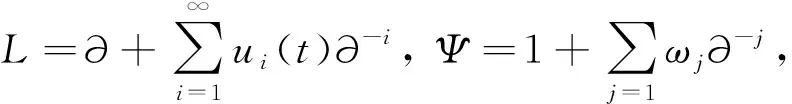
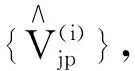
1 BKP系统的弦方程

本节主要证明现有文献中BKP系统弦方程的定义会产生的数学上的矛盾,并对BKP系统弦方程的定义进行重新优化,然后从此定义出发重新计算弦方程的附加对称算子表达式.

本文将BKP系统的弦方程[11]认定为

(2)

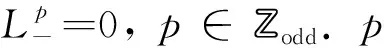
因为弦方程里的Lp是一个微分算子.由于LpL-p=1,故L-p不能等于0.如果L-p=0,则L就是一个等于0的算子,这失去了意义.为了规避L-p=0这个矛盾,文献[3]利用如下方程

(3)

来导出BKP系统的弦方程.而由(3)式和(L-p)-=L-p可得(ML1-2p)-=pL-2p.然而通过计算发现(3)式和BKP系统的弦方程经过如下一些变换仍然会产生L-p=0这个矛盾:

1) 对(L-2pML)-做变换

(4)

2) 对(L-pML)-做两种不同变换

(7)

命题1如果由弦方程限制的Lax算子Lp满足p约化的BKP系统,则下列等式成立

(8)

(9)

2 弦方程约束的算子

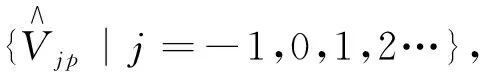
首先,用波函数来表示对称性算子表达式(8)和(9),即让(8)式和(9)式作用在波函数上,可得

(10)

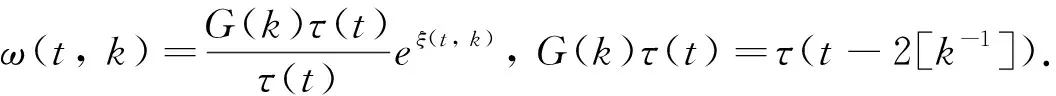
(11)

再将(11)式代入(10)式中,可得到弦方程对p约化的BKP层次结构的τ函数施加的约束方程[3]

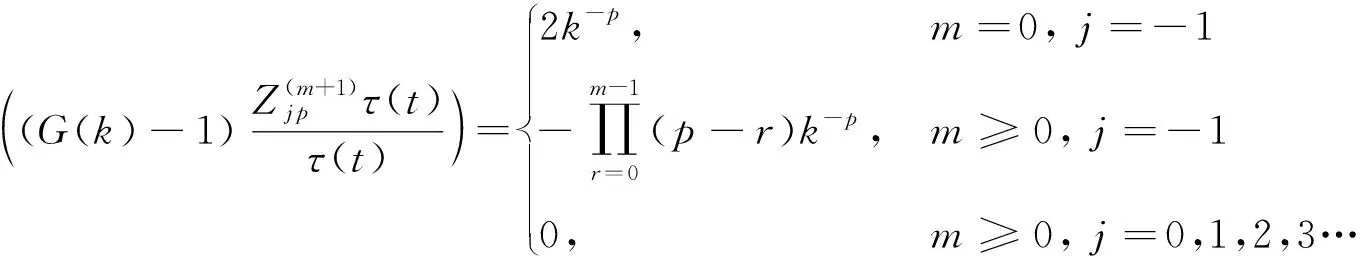
(12)

根据算子G(k)的性质可得

(13)

(14)

然后,从(14)式中确定具体的无冗余变量的弦方程约束算子.为此,先引入顶点算子

(15)

其中

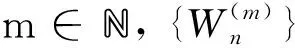
(29)

(30)

其中{cnm,l|m,l∈N,n∈Z},{c′nj,l|j,l∈N,n∈Z}都能计算出.

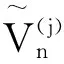
(31)

(32)

(33)

(34)

定理1如果τ函数τ(t)是p约化BKP系统的且满足弦方程,则

(35)

(36)

3 Virasoro代数和p约化的W代数

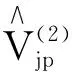
(37)

(38)

接着,计算二阶与三阶的弦方程约束的算子的对易子.

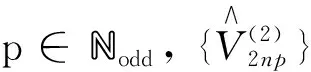
(39)

证通过复杂计算,可以有以下对易子[15]

(40)

然后根据(37)式将(40)式的左边表示成

(41)

通过直接计算可得

(42)

将(42)式和(41)式代入(40)式里,可得

(43)

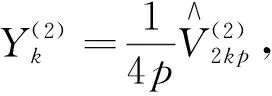
(44)

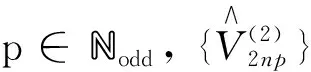
(45)

证计算得到以下对易子[15]

(46)

再将(33)式代入(46)式,可得

(47)

然后,利用(37)式和(38)式将(47)式的左边写成如下形式

(48)

(49)

4 结束语