煤矿地下水库坝基层间岩体破坏及突渗力学模型

王路军,曹志国,程建超,刘升贵,周宏伟,武 洋,王俊光,欧阳迪,薛东杰1,

(1.北京低碳清洁能源研究院 煤炭开采水资源保护与利用国家重点实验室,北京 102211;2.中国矿业大学(北京) 力学与建筑工程学院,北京 100083;3.国能神东煤炭集团有限责任公司,内蒙古 鄂尔多斯 017219;4.中国矿业大学(北京) 能源与矿业学院,北京 100083;5. 辽宁工程技术大学 力学与工程学院,辽宁 阜新 123000)

我国每年煤炭开采产生矿井水约70亿m3,利用率不足30%,每年约50亿m3矿井水不能得到有效利用,相当于我国年工业和民用缺水50%(100亿m3)[1]。黄河流域的晋陕蒙宁甘地区,探明煤炭储量占全国2/3,但水资源不到全国水资源总量3.9%。一方面水资源短缺,严重制约区域发展,另一方面矿井水得不到有效保护与利用[2]。矿井水保护利用成为我国煤炭工业绿色发展和黄河流域生态保护的重大技术难题。

神东矿区经过30余年科技攻关和工程实践,以顾大钊院士为代表的科研团队创造性地提出了煤矿地下水库技术,实现了矿井水资源大规模的保护与利用[3]。技术进步的同时煤矿地下水库矿井水保护理论亟待建立和完善,工程运营中涉及的坝体防渗、多煤层开采安全距离科学确定、水库压煤采掘安全综合评判等,内涵为水库坝基跨尺度破裂突渗建模问题。曹志国等[4]认为宏观尺度上有必要区分导水裂隙带形成的机理差异性,如拉剪混合破坏和纯剪切破坏;李全生等[5]建议可基于导水裂隙带高度提出地下水库安全的可靠评价方法;文志杰等[6]指出研发煤矿地下水库底板渗流模拟试验系统十分迫切。由此可见,物理相似模拟试验仍然是认识煤矿地下水库工程尺度现象的重要手段,如何建立能匹配渗流力学相似尤其是考虑突渗现象的物理力学模型成为挑战[7]。

近年来,随着西部矿区开采深度的增加[8],煤层群开采引发的水库安全评价增加了问题的难度,如采动条件下煤矿地下水库坝基或坝体的安全问题[9]、流固耦合作用下坝基和坝体破坏机理问题[10]等。迥异于地上水库和常规地下水库,煤矿地下水库的坝基和坝体受多重开采扰动影响,与河湖压煤开采[11]、采空区水体下压煤开采[12]存在类似的风险:突发渗透导致的透水安全事故,如新疆丰源煤矿重大透水事故的直接原因是采空区水压力和掘进扰动作用下,隔水煤柱破坏形成突发渗流[13]。以煤层群地下水库为背景,下煤层开采形成导水裂隙带或引起层间覆岩工程损伤,极易发生突渗行为,影响到水库坝基的稳定性,同时也意味着上煤层地下水库“保储蓄”水功能丧失,威胁整体地下水库的安全运营[14]。

力学理论上,突渗是渗流的一种突变行为,主要指渗透率改变引起的流量剧增现象,而导致渗透率突变的直接原因是裂隙网络快速形成进而诱发拓扑连通的改变;间接原因则是诱发裂隙几何产生的开采扰动等行为[15]。因此,在地质条件相对明确的前提下,亟需开展下煤层开采扰动下煤矿地下水库坝基层间岩体裂隙连通产生的突渗现象和力学机理研究,进而指导煤炭与矿井水资源协调安全开采。

1 采动下层间岩体裂隙演化定性分析

1.1 物理模拟试验设计

陕西大柳塔矿作为最早建设煤矿地下水库的矿井,在2-2煤和5-2煤构建了分布式地下水库。两层煤整体上近水平,1°～3°,平均厚度分别为4.5 m (2-2煤)和5.6 m (5-2煤),平均埋深分别为90 m和240 m,层间距约150 m,顶底板主要为细砂岩和砂质泥岩,采用综合机械化一次采全高回采工艺。

以大柳塔煤矿地下水库为工程背景,采用物理相似模拟试验研究2-2煤地下水库与5-2煤层间岩体裂隙演化特征。综合考虑岩层强度、覆岩岩性、模拟尺寸等条件,设置几何相似比为200、容重相似比为1.6、应力相似比为320,采用粒度均匀且颗粒直径在0.05 mm左右的河沙做骨料,石灰和石膏做胶结物进行建模。物理相似模型长、宽、高分别为2.85、0.30和1.41 m,其物理力学参数见表1,监测手段包括应力、位移和散斑测试等综合方法(图1)。工作面开采顺序为2-2煤地下水库、2-2煤采空区、5-2煤回采。2-2煤地下水库由采空区、垮落覆岩、底板、两侧煤柱坝体组成。为了反映地下水库底板承受的覆岩压力和储水压力,2-2煤地下水库区域煤层开挖后安装压水泵传递边界载荷。

1.2 层间岩体裂隙演化规律

5-2煤工作面开采引起上覆岩层运移破坏和裂隙动态演化,对水库右侧煤柱坝体及坝底稳定构成威胁,从而影响地下水库的安全运营[16]。5-2煤工作面开采过程中层间岩体破断特征及裂隙演化如图2所示。随着5-2煤工作面不断推进,层间岩层发生拉裂、直接顶初次垮落、基本顶破断。当工作面推进距上部煤柱坝体水平距离110 m时,离层现象显著,裂隙增多且变宽,形成网络连通雏形;至70 m时,层间覆岩裂隙逐渐向左上方水库坝体方向延伸,坝体底板岩体散斑观测部位多处出现裂隙,但尚未贯通;至10 m时,贯通裂隙形成,扩展至煤柱坝体右侧,煤柱坝体产生损伤破裂。

图3定性描述了相似模型试验中散斑区域中局部宏观裂隙的形成过程,由远至近距离70、57、44、31、18和10 m,裂隙的连通由离散局部变形或小裂隙连通形成宏观裂隙并存在进一步开度增宽的过程;若是存在水力耦合等作用则会加速裂隙扩张和贯通。相似模型中宏观尺度裂隙的贯通并非是一蹴而就的,因此突渗力学行为的几何基础,即裂隙网络形成存在时间尺度和空间尺度2方面因素。

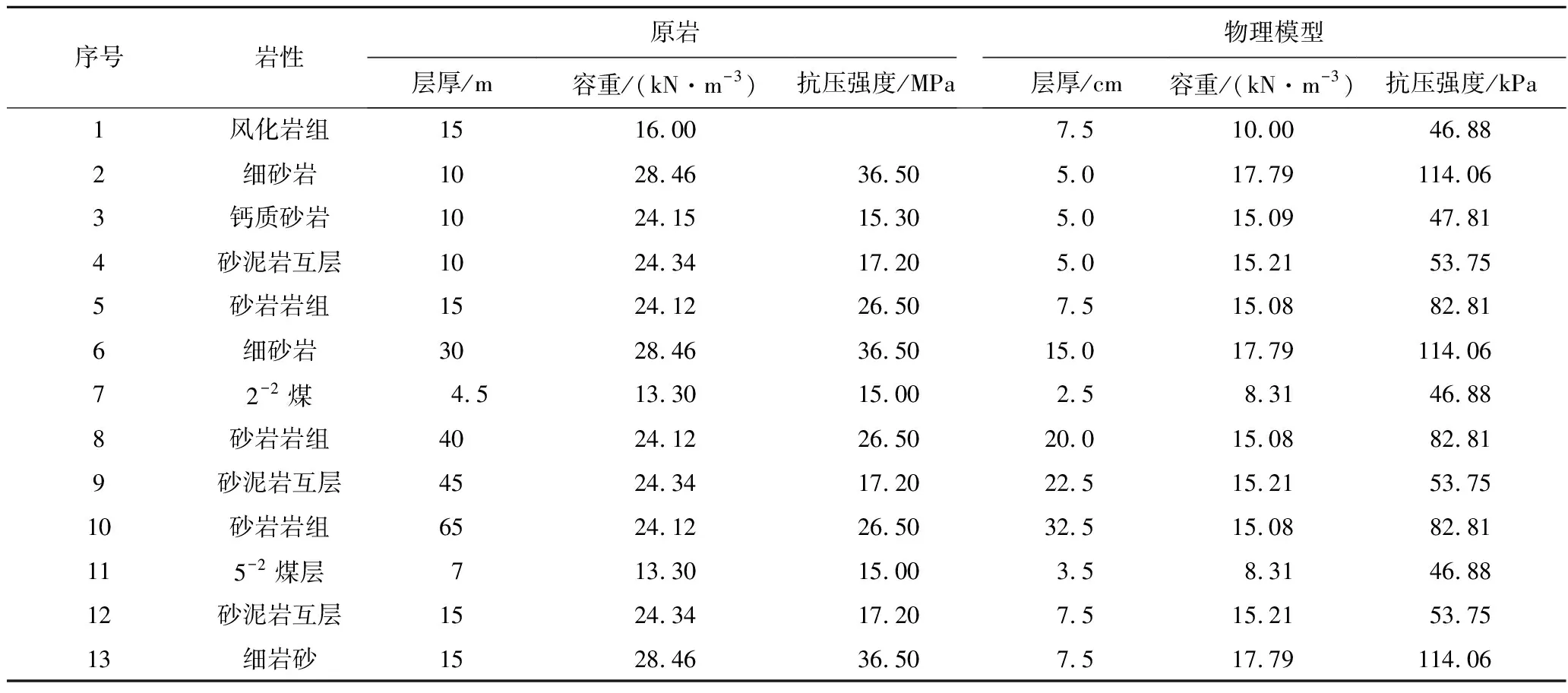
表1 物理模拟试验物理力学参数

图1 大柳塔矿物理相似模型Fig.1 Physical similarity model of Daliuta Mine

图2 层间岩体裂隙演化Fig.2 Fracture evolution in rock mass between two adjacent coal seams

2 层间岩体裂隙网络演化定量分析

相似模型是对地质尺度或工程尺度力学现象的室内再现,多数试验是观察应力、变形等,如采动支承压力分布的演化,较少从几何学和拓扑学上进行阐释,工程中对于裂隙的重视情形基本一致,但对于裂隙网络的认识和理解并不充分。煤矿地下水库突渗的前提是下煤层开采引起的坝基破坏,因此层间网络的几何和拓扑规律演化成为研究重点[17]。

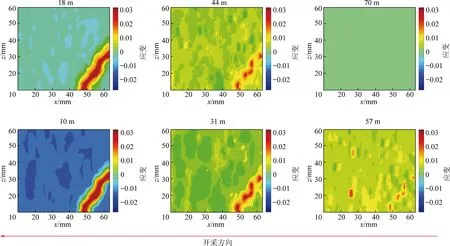
图3 层间岩体局域宏观裂隙贯通过程Fig.3 Connecting process of macro fractures in rock mass between two adjacent coal seams

2.1 裂隙网络几何统计定量分析

将图2中裂隙网络离散化,视裂隙的直线状态为线段、弯折状态为迹线,多个线段构成迹线,由节点相连。图4为开采引起的层间裂隙网络几何统计分布,线段数153、迹线数70和节点数223,线段长度分布多小于1 m(模型中尺寸)且离层裂隙比两端穿层裂隙明显长;线段走向多受控于离层裂隙,穿层破断裂隙角度偏大,范围60°～90°;迹线长度空间分布基本同线段分布,长度3 m以内,考虑几何比,即600 m。将不同长度的线段和迹线进行长度统计,其数量累积分布函数与长度在局域较大尺度上呈现幂律分布特征(图4(e)、(f)),即线性分形特征明显,这与桂乐乐[18]和薛东杰[19]对宏观断层和细观裂隙的观察结果是一致的。

针对上述分段线性分布呈现分形特征问题[20],XIE等[21]、XUE等[19]指出多段线性分形的交叉点除了多重分形特征外,不同因素产生的裂隙往往也会存在尺度跳跃,即在某一尺度存在线性分形不连续,可定义为临界尺度。裂隙网络长度幂律分布和临界尺度的存在从侧面证实裂隙演化在空间上存在强烈的连通概率。因此,从裂隙网络几何和拓扑角度揭示突渗问题有利于揭示其连通本质。

图5为利用小波分析对层间裂隙网络进行图像增强,色阶代表归一化小波系数的值[22-23],测量元尺度a=2.2像素,分别利用2a、4a、8a和16a处理图像,相当于放大尺度重新观察裂隙网络,可见随着观察尺度的变大,裂隙网络整体连通性增强,形态上看,裂隙变粗、连续且离散性消失。因此,大尺度上裂隙分形特征与连通有一定关系。

2.2 裂隙网络拓扑连接分析

裂隙网络连接最重要的是连接点类型,这里考虑I、X和Y型裂隙[24]。图6(a)展示了3种节点类型分布,数量分别对应为0、85和119,也就是说单条孤立型裂隙几乎不存在,Y型连通是X型连通的1.4倍左右。整体上X型主要分布在内部,Y型主要分布在两侧,而在煤层开采上方X型和Y型交错分布,这与离层和穿层裂隙的整体分布规律是一致的。

通过计算,I、X和Y型裂隙可以由三相图直观反映,如图6(d)所示,为相似模型层间裂隙连通水平三相图[25]。可见裂隙整体发育水平高,但不属于完全无序的裂隙,是某一方向主导的裂隙,即离层裂隙主导、穿层裂隙连通的裂隙网络。考虑覆岩非均质性和各向异性引起的渗透率方向差异性,计算渗透张量[26-27](图6(e)),水平方向渗透率约是2.2×10-9m2,垂直方向渗透率约为1.5×10-9m2,即水平方向约是垂直方向渗透率的1.5倍。

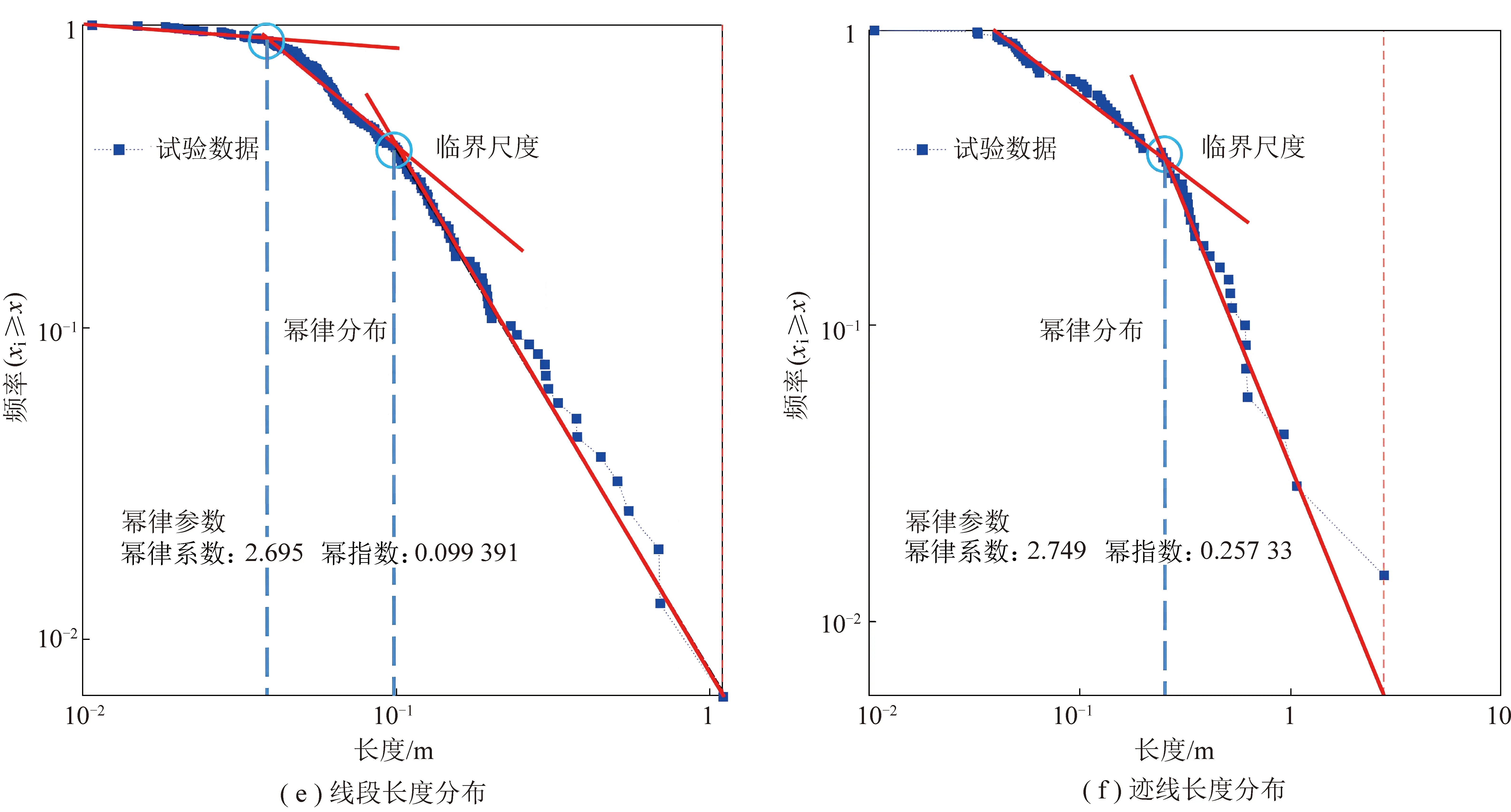
图4 层间裂隙网络几何统计Fig.4 Geometry statistics of fracture network in rock between two adjacent coal seams

3 层间岩石采动应力渗流试验

3.1 三轴循环加卸载力学行为分析

鉴于煤矿地下水库底板岩层以砂岩为主,同时考虑煤柱潜在破坏的影响,选择砂岩和煤体作为试验对象。煤样取自2-2煤层,岩样取自层间覆岩,按国家标准GB/T 23561.1—2009《煤和岩石物理力学性质测定方法》,加工圆柱体试件:高100 mm、直径 50 mm,即高径比为2∶1(图7(a)),三轴循环应力加卸载和渗流试验所用设备为MTS815岩石力学试验机。

相似模型试验中布置的应力盒可以动态监测采动对应力演化的影响,层间覆岩中应力扰动路径包括单调升降、先升后降和先降后升,可见煤层群开采时层间覆岩应力演化的复杂性。图7(a)仅展示了先降后升的采动应力演化规律,本文采动应力路径包括原位应力、初始扰动和三轴循环加卸载3个阶段,同时开展渗透率测试(图7(b))。静水压阶段用于模拟原位应力水平;初始加卸载阶段用于模拟采动开挖起始影响;循环加卸载阶段用于模拟循环扰动影响。首先,静水压力阶段以1 MPa/min的加载速率加载轴压σ1与围压σ3至5 MPa,保持静水压状态;将孔隙压施加至试验预定值P0,加载速率为0.2 MPa/s,在t0时刻控制上下游压差为0.5 MPa,后续渗透压差保持不变并动态控制渗透平衡。其次,在初始加卸载阶段采用应力控制,设定卸载比为1∶3,即将轴向应力卸载至4 MPa,卸载速率为0.025 MPa/s;将围压卸载至2 MPa,卸载速率为0.075 MPa/s。第3,循环加卸载阶段:保持围压为2 MPa,由于峰值应力无法判定,轴向应力按照预估抗压强度σc的25%作为一个梯度进行循环加载,到预定值后卸载至初始偏应力状态,直至试件发生破坏。整个过程采用轴向位移控制模式,加载速率保持在0.005 mm/s,峰值应力判定条件设定为应力跌落幅度大于0.5 MPa,每次加载或卸载后采用脉冲法测量渗透率(图7(c)),直至试验结束。

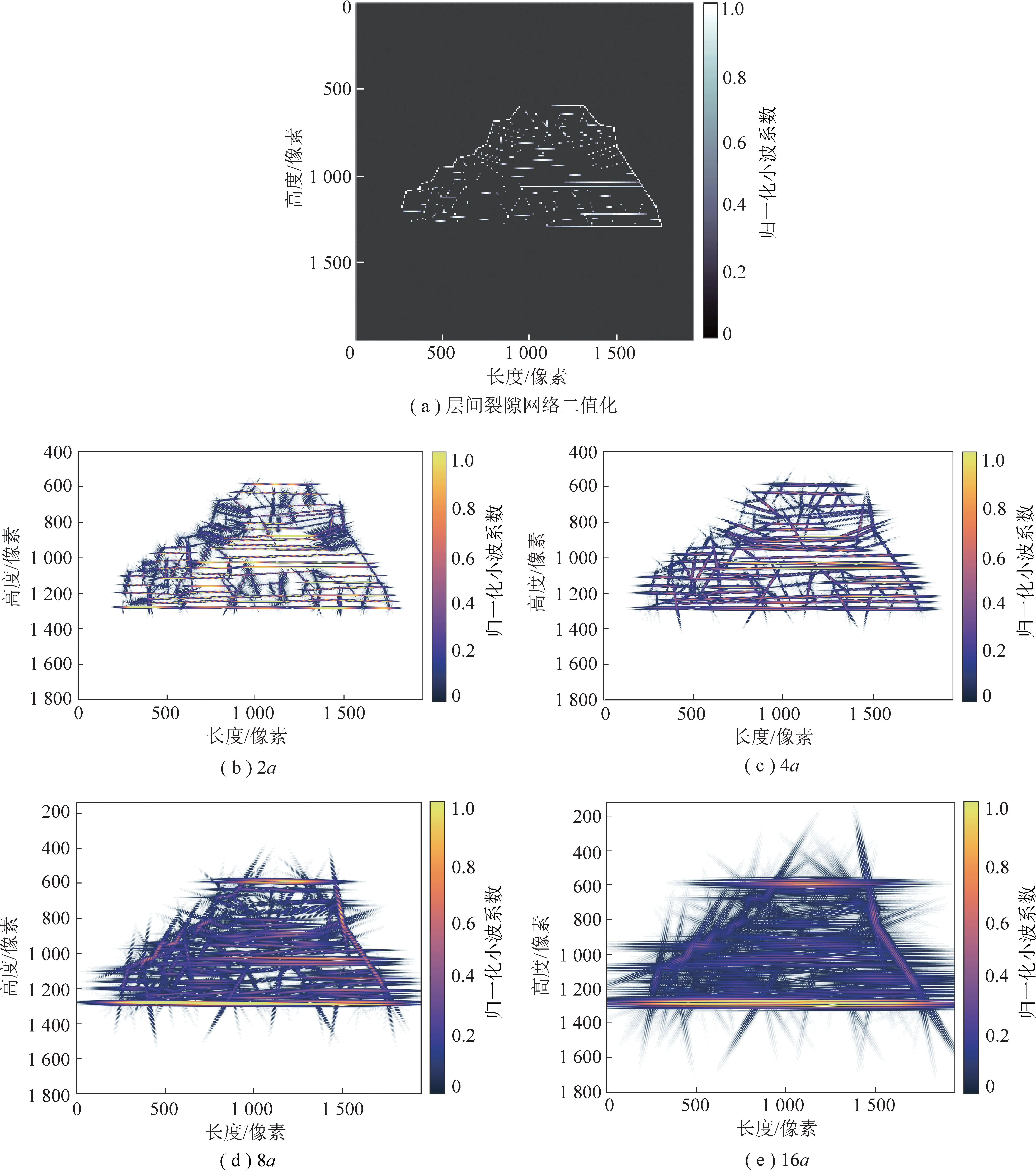
图5 层间岩体裂隙网络形态的小波分析Fig.5 Wavelet analysis of fracture network in rock between two adjacent coal seams

图8、9分别为4组不同初始水压0.2、0.4、0.6和0.8 MPa下砂岩和煤体扰动力学行为曲线,发现采动应力对于砂岩的影响远小于煤体,砂岩峰值应力区间为100.02～149.99 MPa,而煤体峰值应力区间为18.78～34.92 MPa;相应地砂岩变形模量变化范围为15.23～21.70 GPa,煤体变形模量范围为1.25～1.85 GPa。砂岩与煤体强度比例区间:5.33～7.99;刚度比例区间:12.18～17.36。这也导致了煤体在采动应力区明显存在着体积膨胀行为,砂岩则不明显,可见初始开采扰动对于硬质砂岩的损伤水平远不及软质煤体,反过来讲硬质砂岩作为层间岩体中的关键层,其存在有利于抑制地下水库坝底裂隙网络的形成。

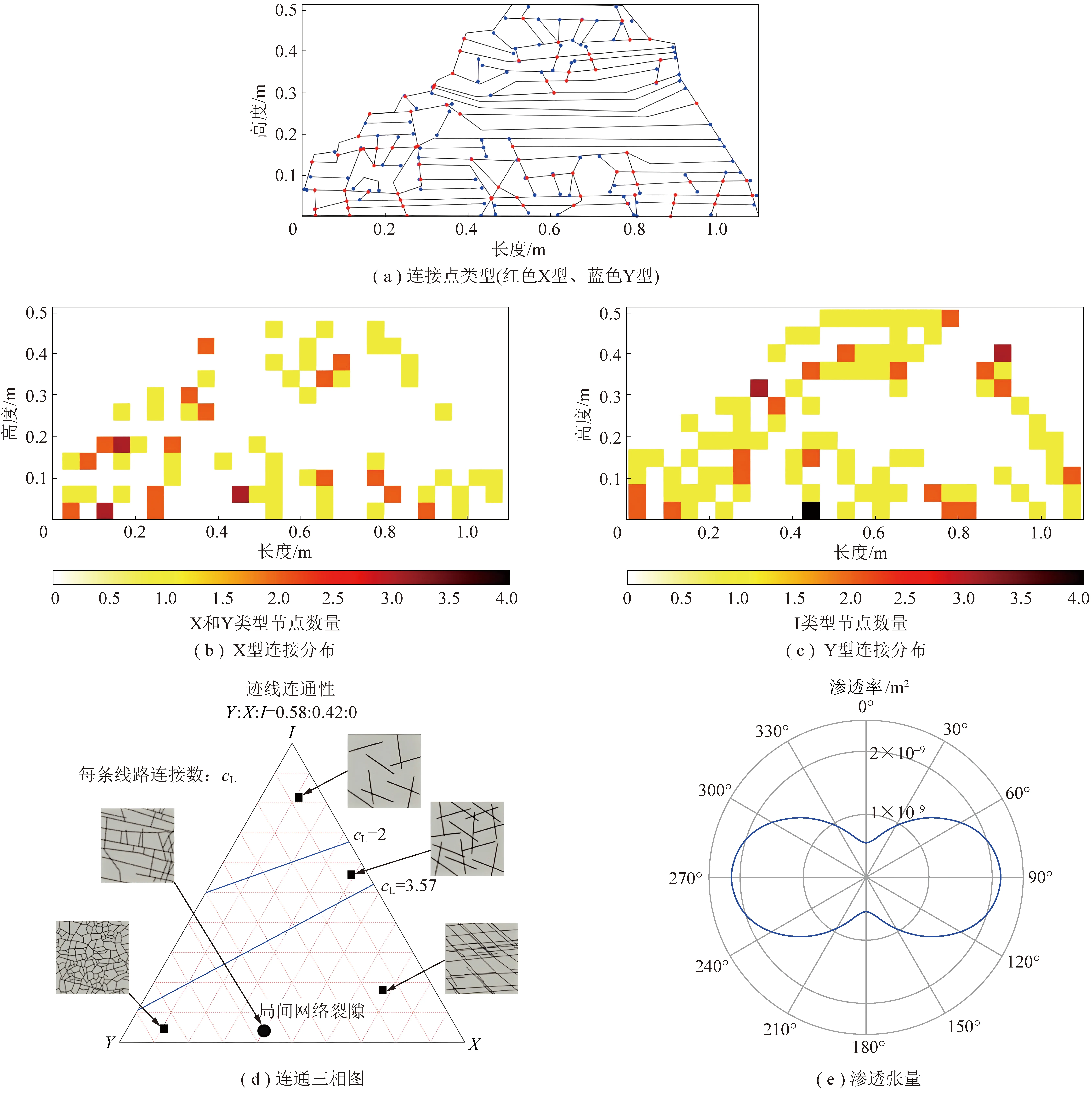
注:I、X、Y分别为含I、X、Y型裂隙的数量。图6 裂隙网络拓扑连接和渗透张量分析Fig.6 Illustration of topological connection of fracture network and its tensor of permeability

另一方面,煤体采动应力卸载阶段产生的体积膨胀变形相当于循环加卸载应力峰值处的体积变形,接近于最终破坏体积变形的一半。如果原位应力高且煤质偏软,采动对应的卸载比过高,煤体完全可能自破坏引发裂隙网络贯通,因此对于煤柱坝体的安全设计需要充分考虑采动应力的影响。

3.2 基于非达西渗流模型的渗透率计算

脉冲法测试渗透率是利用上下端压差随时间衰减的负指数函数计算的[28],但周宏伟等指出压差衰减并不严格满足指数关系,且流体高速渗流呈现非达西非线性特征,采用Mittag-Leffler函数模拟压差衰减特征,创新性地提出了一种基于分数阶理论的岩石渗透率测试计算方法[29-30],区分了达西和非达西模型引起的渗透率测试误差。

图10展示了砂岩和煤体在水压0.4 MPa下渗透率演化趋势,K和Kλ分别为达西和非达西模型计算的渗透率,其中λ为分数阶导数阶次。整体上,考虑Mittag-Leffler 函数计算的渗透率大于常规模型,按照常规模型计算的砂岩渗透率变化不明显,难以反映渗透率微小变化,应力敏感性低;2种方法计算的煤体渗透率演化规律一致,但考虑非达西特征的渗透率是常规方法的1.5～3.0倍。

砂岩渗透率相比煤体小1个数量级左右,在采动应力区煤体体胀效应造成的渗透率上升较大,渗透率增长了3倍;而砂岩渗透率微小波动呈下降趋势。循环应力区,渗透率演化整体上都呈现了先升后降的趋势,由于测试时机不同,主要是围压效应和卸载比的影响,对于煤岩体破坏前后引起的渗透率突增,这类方法仍存在局限性,不利于突渗问题分析。

3.3 岩石力学试验中的激增式力学突渗现象

气渗测试相比液渗方式更为敏感,存在典型的渗透突变行为[17]。煤样经历了线弹性压密、非线性局部破坏与峰值塑性变形阶段、峰后软化阶段至完全破坏;对应体积应变存在压缩增加、压缩减小、体积膨胀、体积急速膨胀阶段,如图11(a)所示。渗透率演化与体积应变演化呈现高度一致性。

如图11所示,偏应力增加是孔隙闭合、裂隙产生的原因,而固体基质体积的改变远小于非连续几何结构(孔隙、裂隙)的改变,因此体积应变的改变主要决定于非连续几何的改变[31]。初始状态,裂隙并未产生,煤作为孔隙介质存在,偏应力较小,孔隙空间压缩,体积应变减小,渗流通道闭合,渗透率对应减小。压缩极限至扩容点,较大偏应力增加将萌生裂纹,微细观裂纹产生,促使裂纹通道连接更多的孔隙。此时体积仍以压缩为主,孔隙-微裂隙通道并未完全形成,渗透率极难出现量级增长,偏应力非线性阶段才出现明显增长,可见非线性偏应力是几何通道连通的重要阶段。峰后阶段,煤样裂隙贯通,应力表现为应力降或应变软化行为,而裂隙几何主导了体积应变的主要组成部分,呈现急剧式增长,对应的渗透通道形成导致渗透率急剧增加[32-33]。

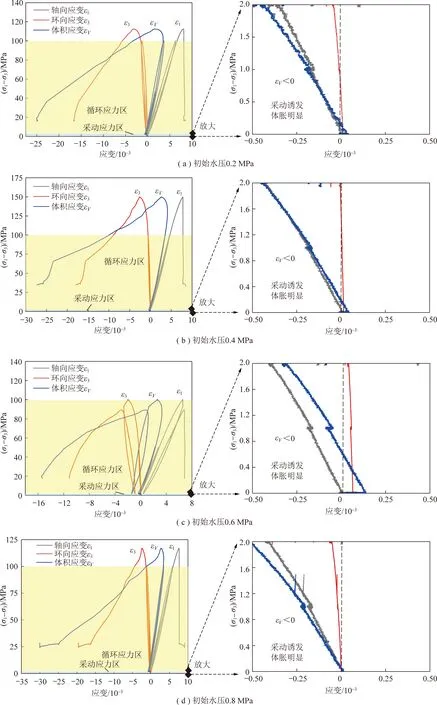
图8 不同水压下砂岩扰动力学行为Fig.8 Evolution of mechanical behavior of sandstone under different water pressures

图9 不同水压下煤体扰动力学行为Fig.9 Evolution of mechanical behavior of coal under different water pressures

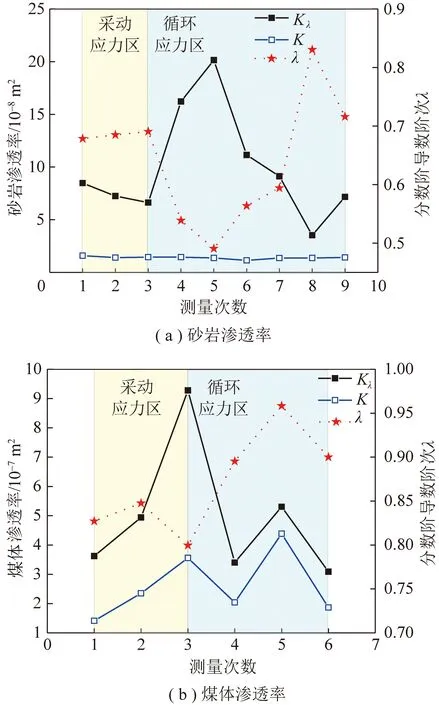
图10 水压0.4 MPa时不同岩性渗透率演化曲线Fig.10 Evolution of permeability of sandstone and coal under water pressure of 0.4 MPa

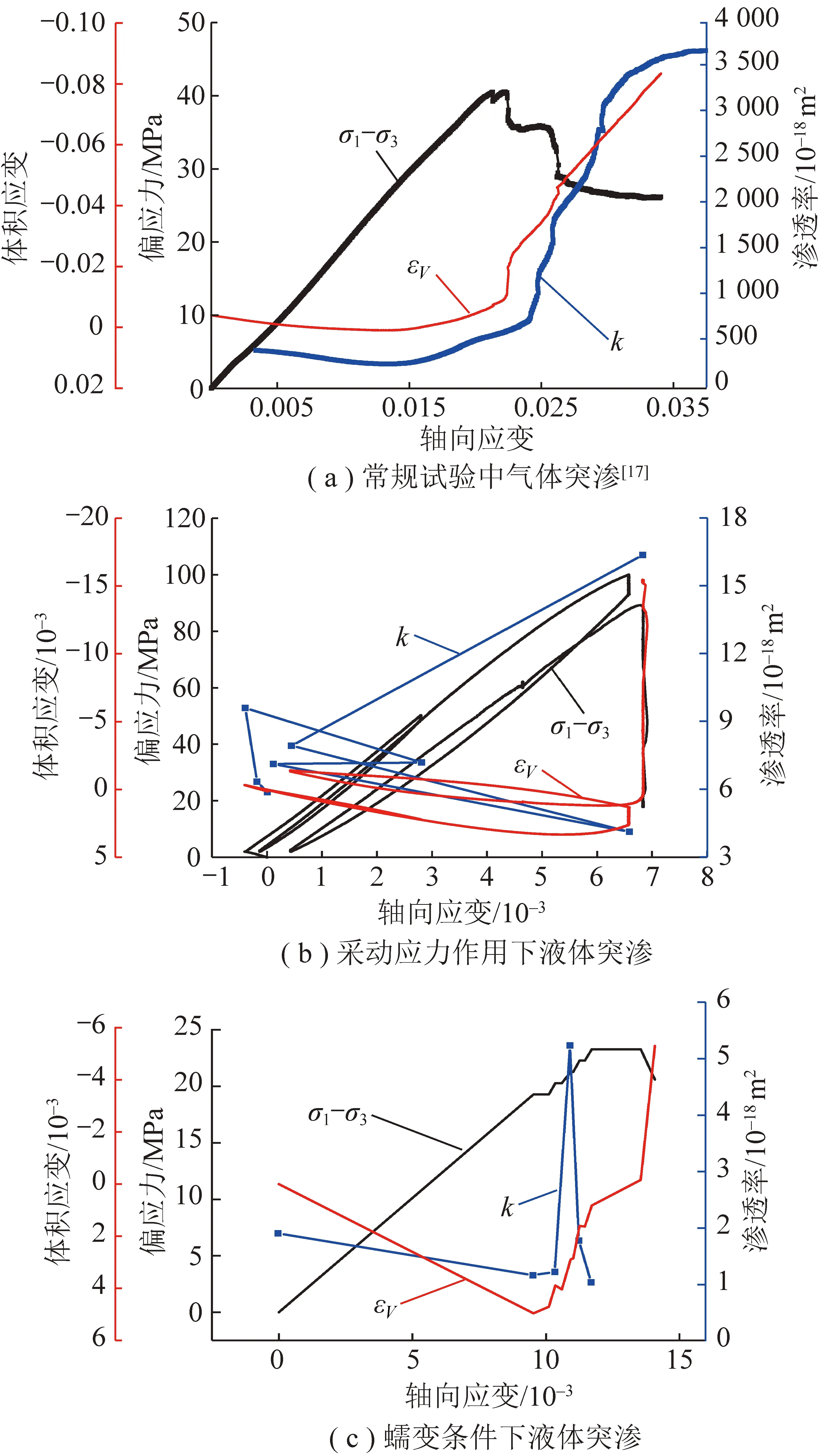
图11 煤体力学试验中破坏激发的突渗行为Fig.11 Jumping behavior of fluid flow induced by failure in coal mechanics test

由此可见,应力驱动因素是外因,渗透率变化的直接原因是内部渗透通道的演化,其主要取决于孔裂隙网络的连通,包括生成、聚合、演化等行为[34],因此直接建立应力敏感性的渗透率模型忽略样品的随机性、裂隙网络的复杂性,从宏观角度把握渗透率定性演化是可行的,但在定量描述其突变行为时存在诸多不确定性,尤其是裂隙网络连通激发的渗透突变,往往对应着轴向应变微变而应力突降等数学上连续但不可导现象,难以在突变阶段建立应力-渗透率的一一映射关系[35],考虑裂隙网络的几何和拓扑成为解决这一挑战的必然。

4 基于逾渗理论的突渗力学模型建立

4.1 突渗现象的力学定义

当前岩体力学仍局限在小变形和连续性假设中,虽然在工程应用中开展了系列的大变形、大位移和非连续破断等试验、数值模拟研究,但在力学理论假设上仍乏善可陈。岩石破坏成离散体对应着连续力学向非连续力学转换、换角度看即离散的孔裂隙连通形成裂隙网络切割连续体;同时若这种破坏加速度效应明显,就必须考虑静力学到动力学的转换;若进一步存在流体耦合现象,流体就会存在动压进而产生突涌等动力灾害。因此,仅仅从材料力学、弹塑性力学基础上思考这些问题,无论是从静动转换、还是破解力学的几何化问题上都存在无法逾越的鸿沟,尤其是突渗通道的形成必须要考虑裂隙网络的拓扑连通等最基础的力学几何化问题。近些年,薛东杰等[36]提 出临界力学原理,基于逾渗原理基本思想考虑岩石材料的不同“相态”,如连续相和非连续相,为力学突变现象的合理解释提供了新的力学视角。

突渗现象发生往往时间极短,伴随应力突降、体应变激增、破裂信号陡增等行为,图11均展示了在轴向应变非常小的变化下,渗透率发生了突增行为,斜率接近无穷大,数学上意味着接近不可导,但物理上仍是连续的,利用临界力学原理可绘制图12,用以描述渗流突变现象。这类现象利用传统力学建模是不理想的,如无法构建同一轴向应变对应无数个应力值的力学模型,类似的也无法建立渗透率激增关系。因此,从宏观力学角度出发,突渗可定义为渗透率的几何量级突增,即最终渗透率是初始渗透率的数倍至千倍甚至更高。需要说明的是,这种突增无论是实验室还是现场测试往往都是迟滞的,这是由于元件的敏感度和反应延迟导致的。

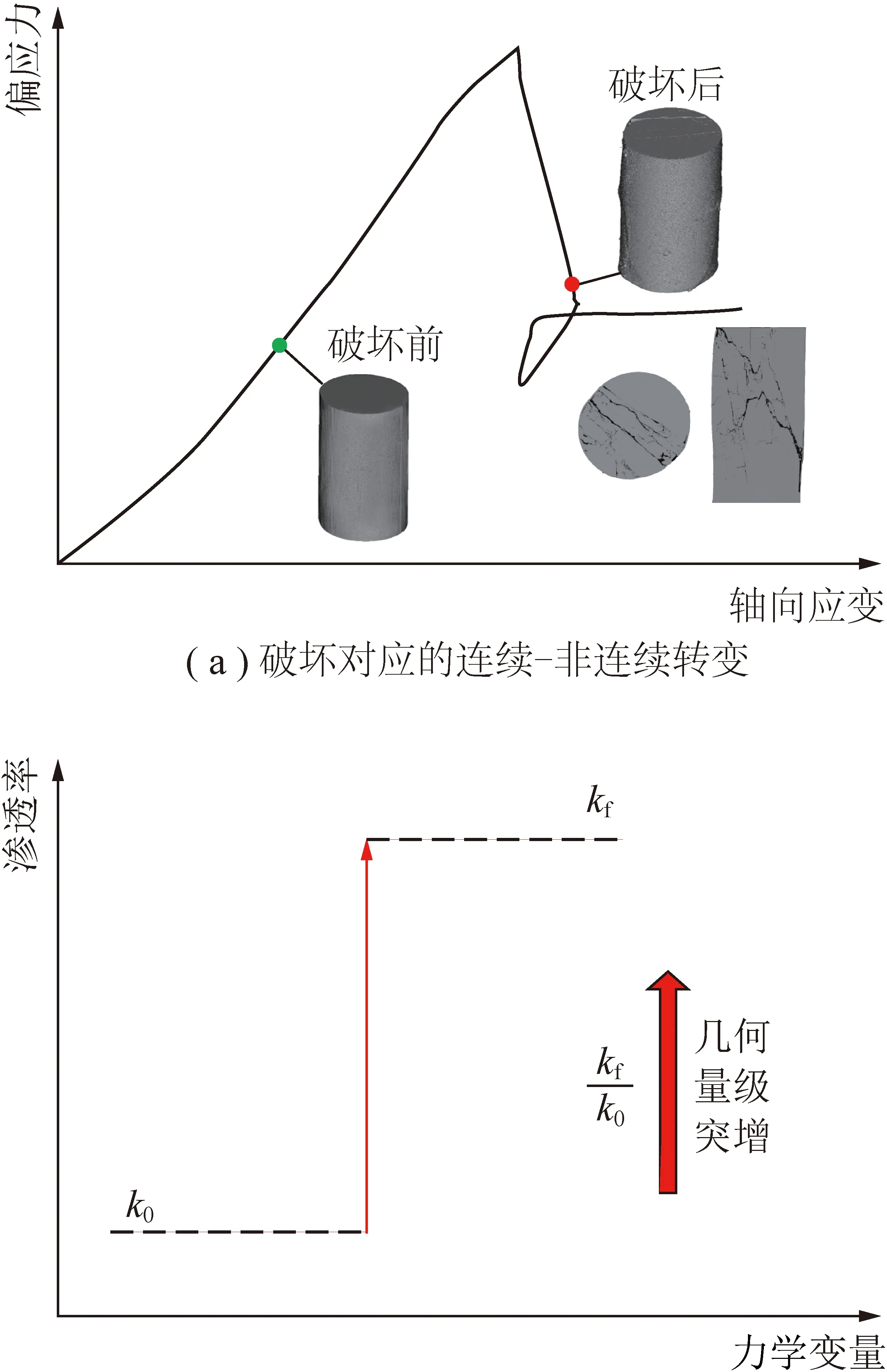
图12 突渗力学概化模型Fig.12 Conceptual model of critical flow behavior

综上,力学上可将突渗定义为

(1)

式中,k0和kf分别为初始和最终渗透率。

上述基于渗透率的突渗定义仍是基于一种宏观或者唯象认识,如渗透率单位可以是达西(D)也可以是平方米(m2),从量纲上看其概念本质是几何。力学的几何化很难突破,谢和平[37]将分形几何引入岩石力学中,主要考虑裂隙粗糙面和裂隙网络中随机性的天然分形性,归类为线性自相似分形和自仿射分形。从原理上理解突渗现象离不开裂隙网络的几何和拓扑化方法,拓扑意味着连通,简言之突渗现象合理解释的基础是拓扑连通,定义如下:

(2)

其中,C为连通率。这里的无穷符号∞对应着无穷导数,现实中kf、Cf都是延迟测试得到的,是一个较大的有限值,不是无穷数,换言之存在数量级变化,对应的比值从数倍至数千倍甚至更大。

4.2 突渗力学行为的逾渗建模

建立应力应变全过程的渗透率模型存在诸多难题。从宏观角度或统计平均角度来看,多数渗透率模型是依赖于达西定律(Darcy’s Law)[38]、立方定律(Cubic Law)[39]和Carman-Kozeny方程,建立渗流变量与应力变量间的关系,难以描述强非线性特征。针对煤体,如SOMERTON[40]、DURUCAN和EDWARDS[41]、MCKEE[42]、SEIDLE[43]和LIU[44-45]建立的理论或经验渗透率模型,分列如下:

(3)

(4)

(5)

(6)

(7)

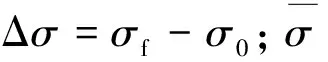
根据3.3节渗透率演化规律及机制可知,偏应力引起的孔隙体积扩张、裂隙接触面与凸起接触减小是渗透率增加的原因之一,但并无法有效解释渗透率的急剧增加[46]。而偏应力引起的基质损伤形成新的连通通道,将孤立的孔隙裂隙连通形成网络才是渗透率急剧增加的基础。而对应偏应力作用的综合几何参量为体积膨胀,因此体积膨胀可以综合反映空隙网络结构的连通状态[47]。

从拓扑连通角度解释更准确,如建立连通率(Conductivity)和渗透率(Permeability)的关系,而连通率通常与裂隙几何和拓扑相关。裂隙几何开闭主要是法向应力控制,而剪切应力将会导致开度在局域尺度上引起法向应力变化,整体上会减小接触面积,增加开度与连通率。从而存在一个应力-应变-连通率-渗透率(Stress-Strain-Conductivity-Permeability)的力学链条,若考虑耦合问题将会更加复杂,但多数模型直接建立应力-渗透率的关系,忽略应变-连通率(Strain-Conductivity)不能从本质上解决模型出现的种种偏差问题,尤其是突渗等问题无法描述。

对于裂隙,应力-渗透率依赖的理论基础是立方定律,这是因为裂隙开度等几何因素是渗透率变化的直接变量,应力是诱发变量。准确地确定裂隙网络的开度目前仍难以实现,而应变作为一种间接测量可以综合考虑网络复杂因素的各种影响,因此建立应变-渗透率(Strain-Permeability)关系是最有效的手段[48]。裂隙网络的随机性导致连通率和渗透率整体上是概率强相关的,即

(8)

式中,p为裂隙网络连通率,是一种概率函数。

根据三轴试验,可以建立依赖体积应变的裂隙网络模型。明显的突变发生在体积膨胀点,而轴向应变与径向应变共同贡献了体积变形。因此可以定义临界概率(Critical probability),pc[17]为

pc∝ε1D+ζ(ε3)

(9)

式中,ζ(ε3)为径向应变的影响。

分形逾渗结构的定量分析可以利用应变的概率密度方程描述[17],即

(10)

当宏细观裂隙网络达到临界状态,整体变形产生的轴向应变达到临界应变ε1D时,此时存在临界概率:

pc=1-e-1=0.63

(11)

联立公式(8)、(9)、(11)与(12),得到基于逾渗理论的轴向应变-渗透率关系:

k=γkf[1-e-(ε1/ε1D)-0.63]2

(12)

式中,γ为常数。

利用式(12)对上述渗透率数据进行理论模型和试验结果比对,考虑流体类别(气体或液体)、采动应力或蠕变条件下突渗行为(图13),逾渗模型均可很好地描述这类突变行为,说明模型整体上有效。

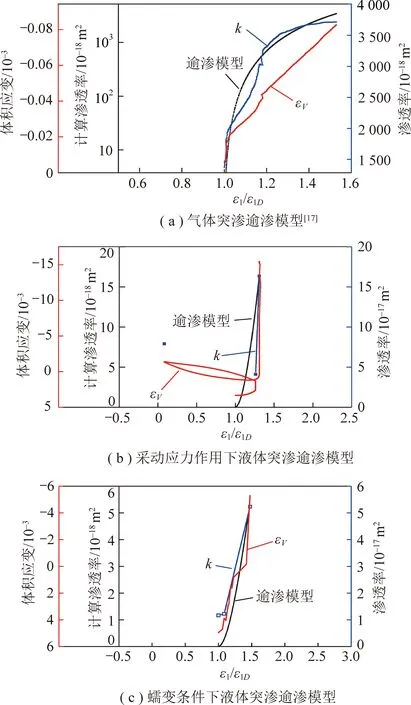
图13 突渗现象的逾渗模型Fig.13 Percolation model of critical flow

4.3 工作局限性讨论

工程岩体中流体的突渗是极其危险的,常导致灾变与重大伤亡,而上述相似模型试验或采动循环加卸载试验都尚未较好地还原突渗现象。突渗本质是渗流力学行为的突变问题,当前无论是科学认识还是力学建模都充满挑战,除了常规的流固耦合问题外,在突渗力学中用到的数学和几何学知识也需要引入新的理论。众所周知,渗流无论是气体还是液体均发生在不同尺度的孔-缝网络中,从微纳米孔到地质尺度断层等,不同尺度均存在着渗透率突变从而流量激增等现象,这主要是由于在外力等复杂因素作用下,内部稳定的通道网络发生了拓扑连接突变,从而导致宏观量发生激变。如室内渗流耦合试验通常采用完整试样在MTS等岩石力学平台上开展研究,无论单轴或三轴状态,完整样品到达峰值前渗透率均不会发生几何级别的突变,反而会存在孔裂隙压密导致的渗透率下降状态,往往峰值前后出现渗透率跳跃现象。

物理相似模拟试验是采矿工程的主流试验之一,但对于突渗模拟仍然具有局限性,材料力学相似并不能严格保证渗流力学相似。以本文开展的物理相似模拟试验为例,下煤层开采确实会导致层间岩体裂隙网络连通并演化成贯通网络直接威胁坝体和坝基安全。这是基于二维物理相似模型得到的定性结论,其中包含3个因素未考虑:第1,地下水库能否像煤层开采一样简化成平面问题尚缺乏研究;第2,二维相似模型弱化了上覆岩层约束条件,垮落效果相比三维要剧烈,即岩石的自稳定性考虑不充分;第3,建立物理模型的参数虽然严格遵循相似原则,但无法模拟岩石的孔隙结构,其内部空隙的几何和拓扑特征更无法考虑。因此在相似模型试验中主要的是施加应力边界条件,缺少了渗透问题的设计,不能完全反映渗透灾变产生的原因。

二维物理相似模型中层间岩体裂隙网络拓展会大于真实三维裂隙网络。从应力相似、渗流相似、几何相似和拓扑相似模拟地下水库仍然存在着相当大的挑战。未来,科学有效地模拟煤矿地下水库层间岩体的破坏仍然存在着很多难题,在借鉴已有压煤等煤层群开采经验和模型的同时,试验和理论创新十分迫切。因此,从裂隙网络几何和拓扑角度分析其演化规律将是破解难题的必经路径之一。

5 结 论

(1)以大柳塔煤矿为原型构建了二维物理相似模拟试验,得到了宏观裂隙演化对煤矿地下水库坝基和坝体的影响规律,揭示了多煤层开采地下水库层间裂隙网络连通属于渐进式,区别于室内岩石力学的激增式连通。从几何和拓扑分析角度证实采动裂隙网络存在典型幂律特征,即分形特征;在线性交界处定义临界尺度,作为几何和拓扑研究裂隙网络突然连通的基础。

(2)开展了多煤层地下水库煤岩体采动应力渗流耦合试验,将采动应力路径设计为3部分:静水压力、初始采动应力和循环应力。结果显示采动应力导致煤体的体胀影响远大于砂岩,砂岩作为硬岩关键层有利于抑制裂隙拓展和渗透增加。采用基于分数阶理论的非达西渗透率公式计算瞬态法测试的渗透率,相比常规计算方法具有更好的灵敏性。针对煤岩体三轴应力渗流试验,将突渗行为概化为轴向应变微变渗透率发生突增或几何量级激增的现象,数学上表现为不可导的曲线。

(3)基于二维相似模型试验、岩石力学试验指出渗流突变的几何基础是裂隙网络连通激增,提出了突渗的力学定义和拓扑定义。将裂隙网络连通视为连续相至非连续相的跳跃行为,建立了描述突渗力学行为的逾渗模型,经验证模型有效且形式简单,为突渗力学行为的数学描述奠定了基础。