基于法兰同轴测试原理的织物屏蔽效能仿真

孙娜 徐阳

摘要： 为了在设计阶段更好地预测和评价织物的屏蔽性能，文章采用CST微波工作室建立了基于法兰同轴测试原理的织物屏蔽效能仿真模型，分析了电磁屏蔽织物两种等效模型的适用范围，并通过织物屏蔽效能测试验证了仿真的准确性。结果表明：仿真模型能够模拟法兰同轴装置对试样屏蔽效能的测试过程;网格模型可作为镀银长丝织物的仿真等效模型，且当织物中纱线截面短轴尺寸小于0.05 mm、孔径率小于0.30时，织物结构可简化为平板模型;不同嵌织比、不同层数的镀银长丝嵌织织物屏蔽效能测试结果与仿真结果在数值和变化趋势上基本一致，平均误差在6%以内，证明采用此仿真模型预测镀银长丝织物屏蔽效能是可行的。

关键词： 法兰同轴法;镀银长丝织物;电磁屏蔽织物;织物模型;电磁仿真;屏蔽效能

中图分类号： TS101.8

文献标志码： A

文章编号： 1001-7003（2023）05-0052-07

引用页码： 051107

DOI： 10.3969/j.issn.1001-7003.2023.05.007

基金项目：

中央高校基本科研业务费专项资金项目（JUSRP52007A）

作者简介：

孙娜（1997），女，硕士研究生，研究方向为功能纺织品。通信作者：徐阳，教授，zh3212@vip.sina.com。

电磁屏蔽织物具有柔软、质轻、强度高等优点，被认为是一种理想的屏蔽材料，广泛应用于电磁兼容和电磁防护等领域［1］。衡量电磁屏蔽织物屏蔽效果的重要指标——屏蔽效能（SE），目前主要通过实验测试获得。但由于织物的柔软性和手工操作的偶然性，使得测试结果不稳定，极大地干扰了织物屏蔽性能的测量;此外测试只能在织物生产后进行，设计周期长、实验成本高［2］。为了在织物设计阶段可以预测其屏蔽性能，进而开发出屏蔽效能好、成本低的电磁屏蔽织物，研究科学有效的仿真方法以预测和评价织物的屏蔽性能成为当前的研究重点。

目前织物屏蔽效能的仿真主要基于屏蔽室法测试原理，通过仿真软件定义织物组织单元周期边界条件，使电场和磁场在样品平面互相垂直分布，从而实现1～18 GHz高频织物结构参数等因素对屏蔽效能影响的分析［3-5］。但由于屏蔽室法测试成本高、对测试技能要求严格，故而在实际生产和研究中多采用设备成台性好、操作简单的法兰同轴法［9］。与屏蔽室法不同，法兰同轴法是针对0.03～1.50 GHz的远场电磁环境测试方法，且电磁场在样品平面的分布更为复杂，因此两者对织物屏蔽效能的测试会存在明显差异［6］。目前尚无基于法兰同轴法的织物屏蔽效能仿真方式。为了更好指导实际生产和研究，本文基于法兰同轴法屏蔽效能的测试原理，采用CST软件建立织物屏蔽效能仿真模型，探讨电磁屏蔽织物等效模型的适用范围，并通过不同嵌织比、不同层数的镀银长丝织物屏蔽效能测试实验，验证仿真模型的有效性。

1 初始模型建立

1.1 同轴测试原理

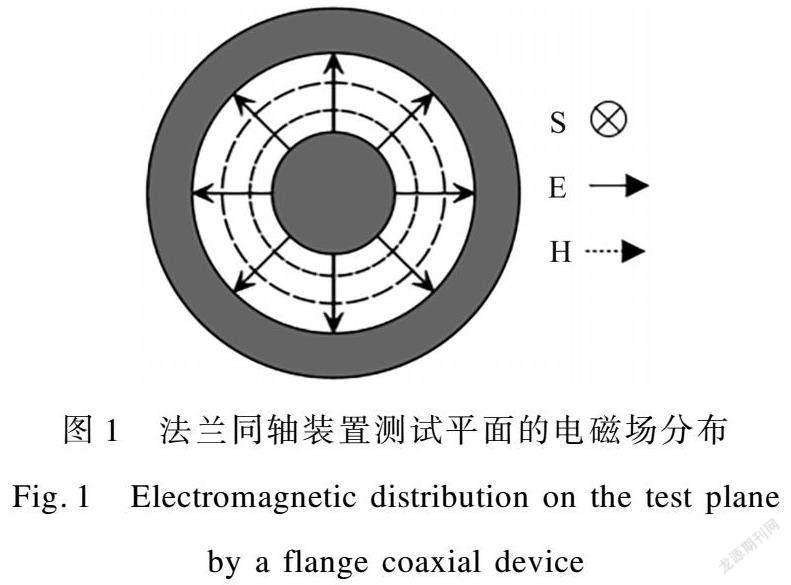
法兰同轴测试技术基于同轴传输线传输主模横电磁波的原理，由于导体的趋肤效应，电磁波通过同轴夹具的内外导体传播，在样品平面分布如图1所示（S为电磁波传播方向、E为电场向量、H为磁场向量）［7］。测试时，在同轴间夹持待测材料，可以模拟远场环境中材料对电磁波的屏蔽效能测试过程。

1.2 同轴测试装置模型建立

法兰同轴测试装置结构如图2所示，其中同轴测试夹具包括左右对称且特性阻抗均为50 Ω的同轴线，2个同轴接口分别连接信号源和信号接收机，两测试夹具之间放置待测屏蔽材料，屏蔽材料厚度需小于最高测量频率波长的1%，即厚度不超过2 mm。

使用CST微波工作室按照標准GJB 6190—2008《电磁屏蔽材料屏蔽效能测量方法》中给出的法兰同轴装置的实际尺寸建立三维模型，为了仿真方便，忽略法兰结构，将测试装置的左右两部分通过内外导体直接连接。在此基础上，增加测量夹具使其满足不同厚度材料的放置，夹具由内外导体两部分组成，尺寸与同轴内外导体尺寸一致，作为法兰同轴的延续体可以在保持同轴良好密封性的同时防止电磁波泄漏，使仿真结果更为准确［8］。同轴装置仿真模型如图3所示，模型内外导体及夹具材料设置为理想导体（PEC），支撑介质材料为聚四氟乙烯（PTFE）。由于电磁波只在内、外导体之间的空腔内传播，因此可以认为结构被嵌入理想导体内部，故设置边界条件为电边界（等效于理想导体，电场垂直于边界表面）、并在同轴接口两端定义激励端口，阻抗均为50 Ω，以使能量能够进入和离开理想导体。为了确认同轴测试装置的传输性能，根据图3模型，采用频域求解器分别在无试样、负载导电试样（电导率1 000 S/m、厚度0.1 mm）情况下进行仿真。

在无试样、负载试样情况下，1 GHz时同轴传输线内电流分布及测试平面的场分布如图4所示。当负载高导电试样时，输入的电磁波被试样反射、吸收，几乎未透过试样，且输出的电磁波强度较无试样负载时显著降低。同时测试平面电场由圆心沿着半径方向传播，磁场沿着平行于圆周的同心圆环分布，与实际测试中试样表面场分布（图1）情况一致，说明该仿真模型能够模拟法兰同轴装置对试样屏蔽效能的测试过程。模型仿真的准确性取决于装置的反射情况，通常采用电压驻波比VSWR。

传输线上相邻的波腹点与波谷点电压振幅之比，其值越接近1，说明装置的反射越小、仿真结果越准确。图5为无试样负载时装置的电压驻波比结果，可以看出在0.03～1.50 GHz频段，VSWR<1.2，可视为电磁波在同轴装置中无损传输，符合标准中对测试用法兰同轴的技术要求。

2 织物模型构建与分析

2.1 织物模型构建

图6（a）所示的电磁屏蔽机织物由经、纬两个方向的镀银长丝交织而成，在织物中形成了交叉处连通的导电网络，具有典型的网格结构，而纱线交织处的孔洞对电磁波几乎无屏蔽作用，因此织物的有效屏蔽结构为导电网格结构，故可以将导电网格结构作为镀银长丝电磁屏蔽织物的等效模型进行理论计算和仿真［9-10］。织物网格模型如图6（b）所示，镀银长丝截面被简化为理想矩形。

式中：k为孔径率，d、t分别为截面长轴和短轴尺寸，w为相邻纱线间距。

但当相邻纱线的间距较小时，其耦合作用导致电磁屏蔽织物没有出现明显的电磁泄漏，呈现出与无孔隙的平板材料相近的屏蔽效能，且电磁泄漏与孔径大小、深度直接相关［11］。因此，当织物孔径率小于某一临界值时不会显著影响其屏蔽效能，织物结构可简化为平板模型，即孔径率k=0的无孔金属板结构。

平板模型较网格模型结构更加规则，网格划分相对简单，因此将织物结构简化为平板模型进行仿真可极大提高计算速度，但需明确模型的适用范围，以确保仿真结果的准确性。

2.2 织物模型的适用范围分析

织物中镀银长丝规格（长轴、短轴）的变化会改变模型孔径大小和深度，影响对电磁波的传输与衰减，进而影响织物模型的适用性。在实际应用中，镀银长丝直径取决于基体长丝（如涤纶、锦纶长丝）直径，其直径大多分布在0.05～050 mm［12］。同时，结合纱线在织物中被压扁这一实际情况，考虑了织物中纱线压扁系数0.65～0.80，最终定义纱线短轴尺寸t在0.03～0.50 mm、长轴尺寸d在0.08～0.80 mm。

在CST中利用Brick（立方体）工具建立不同纱线规格、不同孔径率的网格结构模型，定义网格电导率为1.59×105 S/m，将其夹持在测试夹具之间。按照1.2对仿真条件进行设置，最后采用频域求解器进行求解计算，得到不同纱线规格下屏蔽效能随孔径率k变化的仿真结果，如图7所示。

由图7可知，当t≤0.05 mm时，d=0.1、0.5、0.8 mm的导电网格屏蔽效能均随k值增大而减小，且在整个孔径率范围内（0～1）可以根据曲线拐点k′分为2个阶段：第一阶段，当k≤k′时，由于相邻导电纱之间的耦合效应较强，通过孔隙的电磁泄漏并不大，所以不同孔径率下的导电网格屏蔽效能基本一致，且与孔径率为0的平板结构屏蔽效能近似相等;第二阶段，当k＞k′时，电磁泄漏带来的衰减效应逐渐增加，屏蔽效能随孔隙率增大而下降。图7中k′点孔径率约为0.3，故可取0.3为临界孔径率。仿真中，当织物孔径率低于0.3时，织物模型可简化为平板模型;高于0.3，织物模型则采用网格模型。

当t＞0.05 mm时，孔径率k为0.1～0.4的不同长轴尺寸导电网格屏蔽效能均高于k=0的导电平板屏蔽效能，此时除了相邻导电纱之间的较强耦合作用外，孔径深度的增加也使孔的波导效应随之增大，波导衰减贡献的屏蔽效能SEwg见下式［13］。

式中：c为真空中的光速，m/s;f为入射波频率，Hz;t为孔径深度，m;a为孔径大小，m。

由式（3）可知，当孔径深度较大且孔径尺寸较小时，波导衰减的影响不能忽略，使较小孔径率的导电网格屏蔽效能在相同厚度的导电平板基础上有所增加，故此时临界孔径率不存在，织物屏蔽效能的仿真等效模型仅为网格结构模型。

因此在选择织物模型时，只需考虑织物中纱线的短轴尺寸，当t≤0.05 mm时，可取0.3为临界孔径率，根据织物实际孔径率选择平板模型或网格模型。

3 织物屏蔽效能仿真与分析

为了验证基于法兰同轴测试原理的织物屏蔽效能仿真模型对不同织物结构的兼容性，本文考虑了嵌织间距和织物层数两个因素，选用电导率为1.59×105 S/m的涤纶基镀银长丝织物，建立等效模型，并导入同轴装置仿真模型对其屏蔽效能进行计算。织物几何结构参数如表1所示。

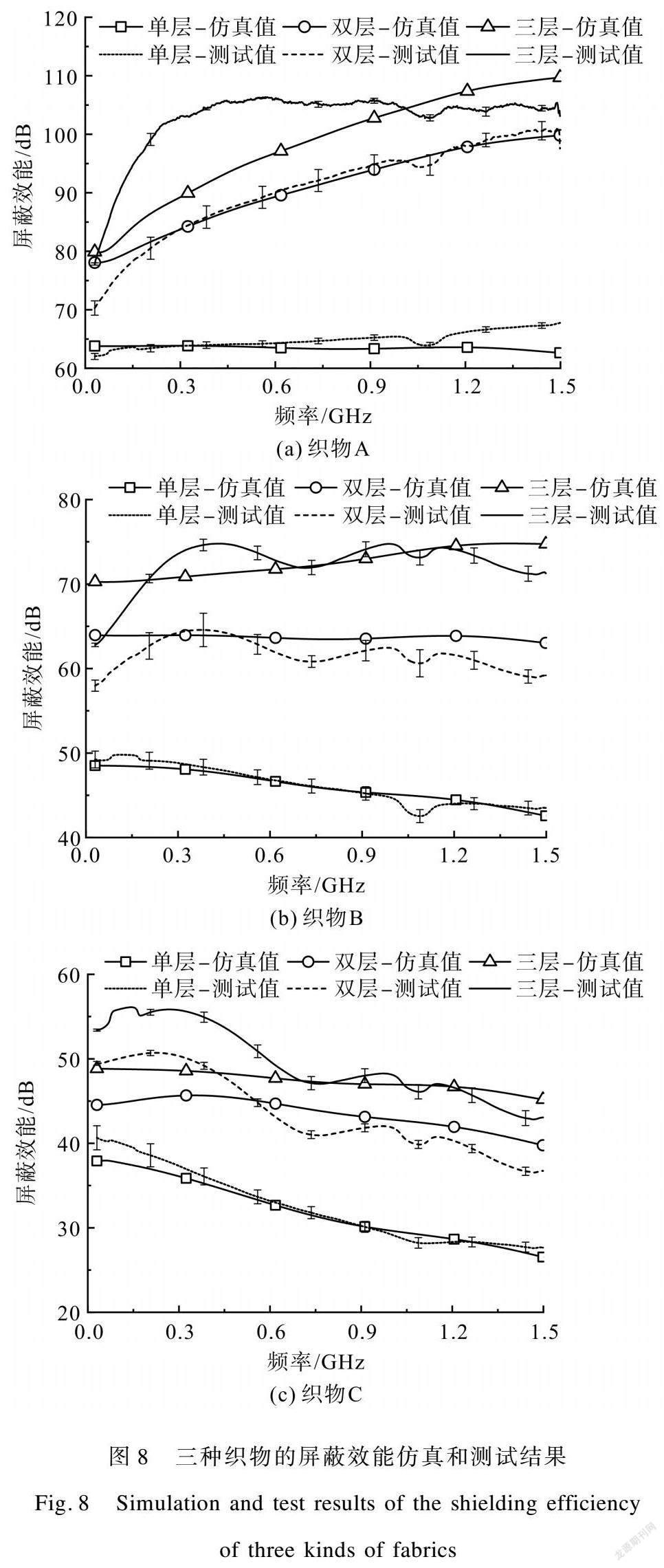
本文参考GJB 6190—2008，采用法兰同轴装置测试织物在0.03～1.50 GHz频率的屏蔽效能，为了提高测试的准确性、减小误差，对每种织物选取3块不同位置的试样并分别测试5次，取其平均值。图8为仿真计算值与实际屏蔽效能对比结果。

由图8可知，三种织物的实测屏蔽效能与仿真結果在数值和变化趋势上基本一致，平均误差在6%以内，并且误差随着层数和嵌织间距的增加而增大。误差的主要原因有以下三方面：一是对织物模型的简化处理，忽视了织物中纱线的屈曲波高，减少了织物内部导电纱线的含量。二是模型认为导电纱线各节点之间接触良好（接触电阻为0），而实际存在一定的接触电阻。但在两者综合作用下，三种织物的单层实测屏蔽效能与仿真结果误差较小，同时随着层数增加，导电纱线含量带来的影响增大，误差也逐渐增大。三是多层织物的叠放位置差异，仿真中织物模型紧密接触且层间导电网格彼此对齐;而在实验中由于织物的柔软性和叠放的紧密程度差异使得织物之间存在一定间隙，层数越多，产生间隙的可能性越大。另外手工操作不免使层间导电网格交错、互相导通，且导电纱线嵌织间距越大，网格间的交错、导通对其屏蔽效能影响越大，因此最大误差发生在织物层数为3层、镀银长丝/涤纶1︰8嵌织时。

对比图8中的数据可以发现，不同嵌织间距、不同层数电磁屏蔽织物的屏蔽效能随频率增大呈现出不同的变化趋势：在单层织物中，织物A的屏蔽效能趋于稳定，而织物B、C呈下降趋势，因为随着织物中镀银长丝嵌织间距的增大，所形成的导电网格孔径率增大，因此在较高频率时电磁波对织物的穿透增加，屏蔽效能的下降幅度增加;在多层织物中，由于织物层数的增加，层间孔隙相互遮挡，限制了电磁波的直接通路，减少了电磁波在高频时的穿透，同时材料整体厚度增大、吸收损耗提高，且吸收损耗与频率正相关，因此织物A、B的屏蔽效能随电磁波频率增大而增大。而织物C孔径率过大，织物层间孔隙遮挡效果不明显，因此其屏蔽效能仍呈下降趋势，但下降幅度明显减小。

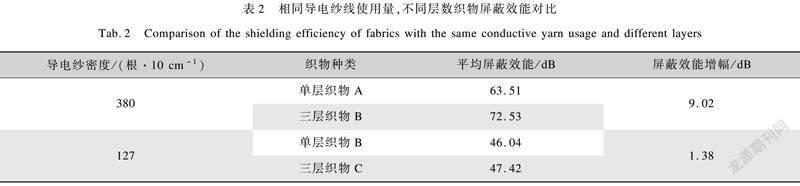
不同层数织物屏蔽效能的仿真和测试结果清晰地表明，随着层数增加织物屏蔽效能随之增加，但屏蔽效能的提高率逐渐降低，同时层数增加意味着导电纱线使用量增加、生产成本提高。为了进一步分析相同导电纱线使用量情况下，织物层数对屏蔽效能的影响，本文以恒定的导电纱线使用量为基准，比较了单层织物A和三层织物B、单层织物B和三层织物C的屏蔽效能仿真结果，如表2所示，仿真中三层织物B、C交错叠放，使相邻导电纱间距分别与织物A、B相同，以消除孔径率的影响。由表2可知，在相同导电纱线使用量情况下，增加织物层数可以在一定程度上提高其屏蔽效能，这是由于导电纱线沿电磁波传播方向的分布增加后，增大了材料内部的吸收损耗和多次反射衰减，因此屏蔽效能提高。同时导电纱线含量越大，层数增加带来的屏蔽效能增幅越显著。

4 結 论

本文基于法兰同轴法屏蔽效能测试原理，通过CST微波工作室建立了0.03～1.50 GHz频段织物屏蔽效能的仿真模型，解决了仅依靠设备测试容易产生较大误差和成本的问题。在此基础上，分析了电磁屏蔽织物的两种等效模型的适用范围，并对镀银长丝织物的屏蔽效能进行仿真，得到以下结论：

1） 织物屏蔽效能仿真计算中，采用导电网格结构作为镀银长丝织物的仿真等效模型，但当纱线截面短轴尺寸小于0.05 mm且孔径率小于0.3时，织物结构可简化为平板结构。

2） 不同嵌织比、不同层数的镀银长丝织物的屏蔽效能仿真和测试结果均具有较好的一致性，验证了仿真模型对不同镀银长丝织物结构的兼容性。

3） 在相同导电纱线使用量情况下，增加织物层数可以提高其屏蔽效能，同时导电纱线含量越大，层数增加带来的屏蔽效能增幅越显著。

最后，由于本文仅以镀银长丝织物为例，对于使用该方法预测织物屏蔽性能是否具有普适性，还有待进一步论证。

参考文献：

［1］闫鑫鑫， 谢春萍， 刘新金， 等. 不锈钢纤维机织物的电磁屏蔽及力学性能［J］. 丝绸， 2018， 55（8）： 29-34.

YAN Xinxin， XIE Chunping， LIU Xinjin， et al. Electromagnetic shielding and mechanical properties of stainless steel fiber woven fabrics［J］. Journal of Silk， 2018， 55（8）： 29-34.

［2］LIU Z， WANG X C. FDTD numerical calculation of shielding effectiveness of electromagnetic shielding fabric based on warp and weft weave points［J］. IEEE Transactions on Electromagnetic Compatibility， 2020， 62（5）： 1693-1702.

［3］孙天， 张一曲， 赵晓明， 等. 纬编针织物电磁屏蔽效能CST仿真分析［J］. 材料导报， 2019， 33（18）： 3130-3134.

SUN Tian， ZHANG Yiqu， ZHAO Xiaoming， et al. CST simulation analysis of electromagnetic shielding effectiveness of weft-knitted fabric［J］. Materials Reports， 2019， 33（18）： 3130-3134.

［4］李建雄， 贾红玉， 陈纯锴， 等. 基于各向异性织物的电磁屏蔽性能仿真计算［J］. 材料导报， 2018， 32（18）： 3235-3238.

LI Jianxiong， JIA Hongyu， CHEN Chunkai， et al. Simulation of electromagnetic shielding performance based on anisotropic fabric［J］. Materials Reports， 2018， 32（18）： 3235-3238.

［5］苏钦城， 赵晓明， 李卫斌， 等. 基于有限积分法的机织物电磁屏蔽效能仿真分析［J］. 纺织学报， 2016， 37（2）： 155-160.

SU Qincheng， ZHAO Xiaoming， LI Weibin， et al. Simulation analysis of woven fabric electromagnetic shielding effectiveness using finite integration technique［J］. Journal of Textile Research， 2016， 37（2）： 155-160.

［6］肖红， 唐章宏， 施楣梧， 等. 织物屏蔽效能的法兰同轴法和屏蔽室法测试对比研究［J］. 纺织学报， 2016， 37（3）： 47-54.

XIAO Hong， TANG Zhanghong， SHI Meiwu， et al. Comparative research on electromagnetic shielding effectiveness of fabric tested by flange coaxial method and shielding chamber method［J］. Journal of Textile Research， 2016， 37（3）： 47-54.

［7］陈超婵， 缪轶， 朱建刚， 等. 电磁屏蔽薄膜屏蔽效能的测量装置［J］. 上海计量测试， 2018， 45（3）： 24-27.

CHEN Chaochan， MIU Yi， ZHU Jiangang， et al. Development on measurement tester of electromagnetic shielding effectiveness for electromagnetic shielding film［J］. Shanghai Measurement and Testing， 2018， 45（3）： 24-27.

［8］李美英. 屏蔽效能测量方法和一种屏蔽材料机理的研究［D］. 北京： 北京交通大学， 2021.

LI Meiying. Study on the Measurement of Shielding Effectiveness and the Mechanism of a Shielding Material［D］. Beijing： Beijing Jiaotong University， 2021.

［9］肖紅， 施楣梧， 钞杉， 等. 机织物有效结构模型的电磁屏蔽效能影响因素［J］. 纺织学报， 2015， 36（7）： 42-49.

XIAO Hong， SHI Meiwu， CHAO Shan， et al. Influential factors of electromagnetic shielding effectiveness based on effective woven fabrics structure model［J］. Journal of Textile Research， 2015， 36（7）： 42-49.

［10］GHIDA A A， LIONE P， LAURENT D， et al. Effective electromagnetic properties of woven fiber composites for shielding applications［J］. IEEE Transactions on Electromagnetic Compatibility， 2020， 62（4）： 1082-1089.

［11］关福旺， 肖红， 施楣梧， 等. 织物基频率选择表面材料的制备及应用［J］. 纺织学报， 2016， 37（2）： 141-148.

GUAN Fuwang， XIAO Hong， SHI Meiwu， et al. Fabrication and application of fabric based frequency selective surface［J］. Journal of Textile Research， 2016， 37（2）： 141-148.

［12］徐克平. 镀银纤维织物的防电磁辐射性能研究［D］. 天津： 天津工业大学， 2012.

XU Keping. Study on Electromagnetic Radiation Resistance of Silver-Coated Fabric［D］. Tianjin： Tiangong University， 2012.

［13］白婉欣. 周期开孔导体板的电磁屏蔽效能研究［D］. 北京： 华北电力大学， 2020.

BAI Wanxin. Research on Electromagnefic Shielding Effectiveness of the Conductor Plate with Periodic Apertures［D］. Beijing： North China Electric Power University， 2020.

Abstract： With the rapid development of information technology， the application of electronic equipment in communication， transportation， finance and other fields increases rapidly， resulting in increasingly severe electromagnetic environment in space. The electromagnetic shielding material is one of the main means to deal with the threat of electromagnetic environment. Among the commonly used electromagnetic shielding materials， the electromagnetic shielding fabric has been widely used because of its characteristics of softness， light weight and high strength. In the development process of the electromagnetic shielding fabric， the development cycle is long because of the complex fabric structure and many influencing factors. In addition， due to the softness of the fabric and the chance of manual operation， the test results will be unstable. Meanwhile， the test and evaluation of the shielding efficiency can only be carried out after the production of the fabric， which further increases the design cycle and experiment cost of the electromagnetic shielding fabric. Therefore， it has become a research hotspot to use scientific and effective simulation methods to predict the shielding efficiency in fabric design stage.

In order to guide the actual production and research， we developed a fabric shielding efficiency simulation method in the frequency range of 0.03-1.50 GHz， aiming at the testing method of flange coaxial fabric shielding efficiency with good platform performance and simple operation. Firstly， the structure model of the flange-coaxial device was constructed by CST microwave studio. Combined with the shielding efficiency test principle of the flange-coaxial method， simulation parameters were set and preliminary simulation was carried out to confirm the transmission performance of the device. Then， two equivalent models of the electromagnetic shielding fabric were established and their application range was analyzed. Finally， the shielding efficiency of silver-coated filament fabrics with different interweave spacing and layers was calculated by simulation， and the accuracy of the simulation was verified by fabric shielding efficiency tests. The results show that the simulation model can simulate the testing process of the shielding efficiency of the flange coaxial device. The mesh model can be used as the simulation equivalent model of the silver-coated filament fabric， and the fabric structure can be simplified into a flat plate model when the short axis size of the yarn section is less than 0.05 mm and the aperture ratio is less than 0.30. The test results of shielding efficiency of the silver-coated filament woven fabric with different embedding ratios and different layers are basically consistent with the simulation results， and the average error is less than 6%， which proves that the simulation model is feasible to predict the shielding efficiency of the silver-coated filament woven fabric.

In this paper， a fabric shielding efficiency simulation model based on the flange coaxial test principle is established， and it can quickly calculate the shielding efficiency of the silver-coated filament electromagnetic shielding fabric， shorten the experimental period and reduce the experimental cost for the design of this kind of electromagnetic shielding fabric. However， as the types of electromagnetic shielding fabrics also include surface metallized fabrics， metal fiber blended fabrics and conductive nonmetallic fabrics， this paper only takes silver-coated filament fabrics as an example. Whether this simulation model can be used to predict the shielding effectiveness of other types of electromagnetic fabrics needs further demonstration.

Key words： flange coaxial method; silver-coated filament fabric; electromagnetic shielding fabric; fabric model; electromagnetic simulation; shielding efficiency