结构纹理感知下的鲁棒光流估计及人脸活检应用

蔡泽民，廖小鑫，赖剑煌，陈军

1.汕头大学工学院电子系，汕头 515063；2.广东省数字信号与图像处理技术重点实验室，汕头 515063；3.中山大学计算机学院，广州 510006；4.机器智能与先进计算教育部重点实验室，广州 510006；5.佛山科学技术学院工业设计与陶瓷艺术学院，佛山 528000

0 引 言

光流估计作为计算机视觉的一个重要研究方向，在人群运动分割（Liu 等，2020b）、物体跟踪（You等，2021）、视频动作识别（Solmaz等，2012）和流体运动估计（邵绪强 等，2021）等方面有着广泛应用。尽管光流在计算机视觉领域受到了研究者的关注，但复杂背景条件下精确估计光流仍然存在许多挑战（张聪炫 等，2017）。本文提出一种基于STAR（structure-texture aware retinex）解耦的光流估计方法。首先采用结构纹理感知的Retinex 模型（STAR）将图像中的光照分量与反射分量分离。图1 是STARFlow 解耦过程的可视化结果，其表明STAR 图像解耦能在不影响结构细节情况下显著降低原视频帧的光照变化，与Wedel 等人（2009）提出的结构纹理分解方法相比，STAR解耦结果包含更丰富的细节信息，有助于提高光流计算的鲁棒性。为了在计算光流时保持良好的运动边缘，使用L0梯度最小化对模型进行平滑稀疏约束，以全局约束速度场分量非零元个数。此外，本文给出了求解新模型STARFlow的数值解法。在3 个具有挑战性的公开数据集上所进行的评估，验证了STARFlow方法优于众多基于变分框架及基于深度学习框架的光流估计方法。为了验证STARFlow 方法在生物特征识别应用上的有效性，本文通过STARFlow 提取脸部运动光流特征，在CASIA（Institute of Automation，Chinese Academy of Sciences）人脸反欺诈数据集上进行了人脸活体检测实验，实验结果进一步验证了本文方法在不同光照条件下具有良好的鲁棒性，更适合于人脸活体检测应用。

图1 图像解耦结果Fig.1 Image decoupling （（a）two consecutive frames in alley_2 （clean set）of MPI Sintel dataset；（b）visualization results obtained by the structure-texture method proposed by Wedel et al.（2019）；（c）visualization results obtained by the STAR decoupling method）

本文基于图像序列STAR 解耦，采用L0 平滑稀疏约束，建立起复杂环境下鲁棒光流估计模型STARFlow，保留了更多的运动细节，并给出了模型求解方法。

1 相关工作

近年来，大多数光流计算方法致力于在理想条件下提高光流估计精度（付婧祎 等，2021）。然而，连续图像间的光照变化可能非常复杂，在许多实际应用场景中，光流估计仍然面临重大挑战。为了提高光流计算对光照变化的鲁棒性，研究人员付出了很多努力。Brox等人（2004）采用亮度梯度恒常性假设作为变分模型的数据项约束，取代了众所周知的亮度恒定假设。同时，采用了由粗到细的流动扭曲技术，获得了高精度的光流场。然而，无论是亮度恒定假设还是亮度梯度恒定假设都无法准确建模光照变化，使得光流计算总是对光照变化敏感。Zimmer等人（2011）开发了一个补充框架，将数据项和正则化项中的可用信息结合起来。为了实现对光照变化和异常值的鲁棒性，模型在HSV（hue，saturation，value）颜色空间中采用了约束归一化和高阶恒定假设。Molnár等人（2010）提出了一种基于归一化互相关变换（cross-correlation transform，CT）的变分方案，适用于彩色和灰度序列。在此之后，Drulea 和Nedevschi（2013）提出了一种快速且可并行化的基于块的最小化方法，使用零均值归一化互相关作为块之间的匹配成本。Fang 等人（2013）为块匹配方法引入了正负投票策略。结果表明，与亮度恒常性假设相比，基于CT 的块匹配方法对光照变化更具鲁棒性。Chen 等人（2018）提出的基于Split-Bregman的光流模型在处理光照变化时沿用了Drulea 和Nedevschi（2013）提出的零均值归一化互相关方法。然而，基于互相关的光流方法仅在每一个图像块周围环境和中心像素之间具有相同的局部概率信息。韦伯定律可以应用于各种感觉模式（亮度、响度等），在此基础上，Mei 等人（2020）给出一种高效的全变分光流方法，称为加权正则化变换（weighted regularization transform，WRT），该方法优化了韦伯定律，以在光照变化条件下提供鲁棒的光流估计。然而，传统的基于块的数据项，包括人口普查变换（census transform，CT），由于其局部表面的强烈变化，导致无法处理尺度变化。

对连续两帧图像的预处理也为提高光流估计的鲁棒性提供了思路。Mileva 等人（2007）通过图像归一化、对数导数和颜色空间转换获得了光流计算中的光照不变量，采用Brox 等人（2004）提出的变分框架，提高了光流估计精度，但计算复杂度高。Wedel等人（2009）提出了一种图像分解方法，以消除光流估计中光照变化的影响，虽然该方法对光照变化具有鲁棒性，但由于图像分解中的信息丢失，其精度性能（如平均端点误差（end-point error，EPE）和平均角误差（average angle error，AAE））不够好。Kumar 等人（2013）提出了另一种解耦方法，以提高光流对不均匀光照的适应性。在计算光流时，将反射率和光照分量从图像亮度中分离出来，并结合了更优的反射率恒定性假设。然而，该方法并未将图像中的光照分量完全分离，反射分量中仍包含许多光照变化成分，导致模型在处理明显光照变化时鲁棒性不佳。

由于模型固有的不适定性，计算光流时通常需要正则化处理。在局部处理方法中，如Lucas-Kanade 所提出的，正则化是通过施加局部运动模式（恒定运动、仿射变换等）隐式实现的。在全局技术中，Horn 和Schunck（1981）所提出的稠密光流，通过使用显式Tikhonov正则化来增强目标运动场的全局平滑性。Tikhonov 正则化通常使用L2 范数，并通过保持小振幅系数均匀分布使其最小化，从而在光流计算中捕获全局模式。与L2 范数不同，L1 范数的最小化倾向于产生许多零系数或小振幅系数，而很少产生大振幅系数。对于离散信号，L1范数比L2范数能得到更好的结果。Bruhn 和Weickert（2005）提出一种新方案，通过使用L1 范数代替L2 范数来提高光流估计的精度，并获得了实时性能。现有变分光流模型在处理正则化问题时仍然采用传统的L1范数和L2 范数。图2 是Middlebury 数据集中的Grove3 序列的光流可视化结果。其中，图2（b）为基于L2 范数正则化的H&S 方法估计结果，图2（c）为基于L1范数正则化的TV_L1方法计算结果，图2（d）为基于L0 范数正则化的STARFlow 光流计算结果。使用L1 或L2 范数正则化可以产生平滑流场并保持运动非连续性。然而，如图2（b）（c）所示，计算结果丢失了精细尺度的运动结构并产生过多的分割伪影。

图2 Middlebury数据集上Grove3序列的光流可视化结果Fig.2 Optical flow visualization results of Grove3 sequence on Middlebury dataset（（a）ground-truth；（b）H&S；（c）TV_L1；（d）STARFlow）

2 Retinex感知解耦

本文方法在计算光流时，不是直接依赖亮度恒常性假设，而是采用结构纹理感知Retinex 模型，将图像亮度解耦成反射和光照分量，从而可单独执行反射或光照恒常性假设。

Retinex 模型用于建立人类视觉系统的颜色感知模拟（Land，1977），其物理目标是将观测图像分解为光照和反射分量，该模型可表示为

式中，L表示场景的光照分量，R代表场景的表面反射分量，⊙表示矩阵点乘。然而，Retinex 解耦问题是高度不适定的，还需增加适当的光照和反射先验来正则化解空间。定性地说，光照成分应该是分段平滑的，其捕捉的是场景中对象的结构；而反射分量主要呈现观察场景的物理特征，负责捕捉纹理信息（Wei 等，2009）。为了获取图像的结构纹理信息，引入平均局部方差滤波器（mean of least variance，MLV）（Cai等，2017），该滤波器可表示为

式中，Ω表示对应I中每个像素邻域的局部块（Danon等，2019）。|Ω|表示Ω中的元素个数。由于式（2）描述的MLV 滤波器更倾向于捕捉结构信息，因此不能直接应用于Retinex 解耦。如Retinex 理论所述，较大的导数归因于反射率的变化，而较小的导数则出现在平滑光照中。因此，考虑引入一种指数形式的局部导数，用于灵活调控结构和纹理估计。具体而言，通过控制指数的增长或衰减，使局部导数能更清楚地反映相应的内容结构或详细纹理，从而能更灵活地应用于结构和纹理解耦（Xu 等，2020）。指数化平均局部方差滤波器（exponential mean of least variance，EMLV）可表示为

式中，γ是用于控制图像I的梯度敏感度指数。通过对指数γ的分析，当γ= 0.5时，EMLV滤波器能更好地显示图像纹理，而当γ≥1 时，EMLV 滤波器更倾向于提取结构边缘。基于上述观察，得到一种初始化方案，即设置L0=R0=I0.5，同时建立相应的加权矩阵

式中，γδ＞1，γt＜1 用于调节光照和反射解耦时的结构和纹理感知，⊘表示点除运算，ε为常数，本文ε= 0.001。由此得到一种基于结构纹理感知的Retinex 图像解耦模型（structure-texture aware retinex，STAR），其能量泛函可表示为

式中，S0和T0是式（4）（5）中定义的加权矩阵，分别表示光照分量的结构图和反射分量的纹理图。φ和ψ是比例系数，用于调节数据项和正则化项之间的比重。式（6）中的目标函数涉及光照变量L和反射变量R，它们是可分离的，且分离后的子问题是凸问题，考虑采用交替求解的方式。记Lk和Rk为第k次迭代时得到的光照和反射分量，K代表最大迭代次数，则变量Lk和Rk的更新方式如下：

1）固定R，更新L。

在第k+ 1 次迭代时，关于L的优化问题可表示为

为了求解问题（7），考虑将方程矢量化。为此，使 用 矢 量 化 操 作 符vec( ·)，定 义i=vec(I)，l=vec(L)，rk=vec(Rk)，s0=vec(S0)。将具有前向差分离散梯度算子的Toeplitz 矩阵记作G，则Gl=vec(∇L)。记Drk= diag(rk)和Ds0= diag(s0)分别表示以rk和s0为主对角线的矩阵，则问题（7）可转化为标准最小二乘回归问题，即

通过对式（8）求关于l的导数，并将导数值置为0，可得到相应的解为

最后，将式（9）逆矢量化，得到相应的矩阵形式解为Lk+1=vec-1(lk+1)。

2）固定L，更新R。

由式（7）获得Lk+1后，可类似得到关于R的优化问题

近似地，可将问题（10）重新表述为矢量化格式，记r=vec(R)，t0=vec(T0)，Gr=vec(∇R)，Dlk=diag(lk+1)以及Dt0= diag(t0)，则问题（10）转化为一个标准最小二乘回归问题，即

同样，通过对r求导并置为0，可得到相应的极值解，即

将式（12）逆矢量化，得到相应的矩阵形式解Rk+1=vec-1(rk+1)。

由于目标函数（6）是凸函数，具有全局最优解，因此上述算法是收敛的。

3 基于结构纹理感知解耦的光流估计

Horn 和Schunck（1981）提出的H＆S 光流是经典的光流估计算法，常作为初始光流。该方法基于亮度恒常性假设，表达式为

式中，I(x，y，t)表示t时刻(x，y)处的亮度值，(dx，dy)是连续图像帧同一像素点的位移矢量。为了后续表示 方 便，将 上 述 向 量 分 别 记 做x=(x，y，t)，f=(dx，dy，dt) =(u，v，τ)，u为水平方向速度，v为垂直方向速度，τ为两个连续帧之间的时间间隔。则式（13）可表示为

为使估计误差最小化，采用平滑约束项对光流场进行局部约束，并将光流估计问题转化为能量泛函最小化问题。记H＆S 光流法的数据项为E′data，用于惩罚偏离亮度恒常性假设的情况，则相应的表达式为

式中，Ω表示图像计算域。

3.1 模型数据项

由式（15）两边取对数，可得

将解耦操作（式（1））作用于式（16）两边，有

该表达式有效分解了光流计算中的反射与光照成分，从而可以分别惩罚与反射恒常性假设和光照恒常性假设相关的偏差。由于反射成分不受光照变化影响，相对于光照恒常性，反射恒常性假设应当得到更充分的保障，以提高光流对光照变化的鲁棒性。因此，在进行光流估计时，反射和光照分量按一定比例融合，其中反射分量应占主导。相应的加权表达式为

式中，ξ控制着反射恒常性假设与光照恒常性假设的相关偏差。

更进一步地，采用滤波方式提取光照分量中的有用信息，相应的滤波操作可表示为

式中，L表示经滤波后的目标图像，L′代表滤波前的原图像分量，Fl是5 × 5 的低通滤波器。由此，经过加权和滤波处理后的数据项可表示为

将式（20）中与反射恒常性假设和光照恒常性假设相关的偏差惩罚项进行泰勒展开，可得

因此，有

式中，Lx，Ly，Lt分别表示滤波后光照分量L对x，y，t的偏导，而Rx，Ry和Rt分别代表反射分量R对x，y，t的偏导。u和v分别表示图像像素点的水平速度分量和垂直速度分量。由式（22）整理得到新的光流约束方程，可表示为

由此，得到最终的模型数据项为

3.2 L0范数正则化

为了光流计算时能保持良好的运动边缘，受Xu等人（2011）优化框架的启发，采用L0 梯度最小化方式对光流场进行平滑处理，正则化项可表示为

式 中，∇u=[∂xu，∂yu]T，∇v=[∂xv，∂yv]T。‖ ∇u‖0和‖ ∇v‖0分别为二元函数，定义为

则式（25）中图像域Ω内L0范数度量可表示为

式中，#表示计数运算符，式（28）（29）度量的是光流场水平分量u和垂直分量v的非零梯度个数。up和vp分别代表u和v分量在像素点p位置的水平和垂直梯度。

显然，当连续帧之间存在一些大的差异时，例如第1帧某些区域存在非零梯度值，而第2帧相应区域梯度为零，此时光流场梯度应具有稀疏性。基于此，本文提出了一种新的正则化函数，通过梯度L0 范数对模型进行平滑约束。采用稀疏梯度计数方式，可约束非零流动梯度的数量，以恢复重要的运动结构。

4 光流模型求解

为了从式（23）求解获得光流场(u，v)，可最小化STARFlow模型，具体为

式中，α用于调节数据项和平滑项之间的比例关系。该能量泛函采用L1 范数度量数据项的惩罚以处理光流场异常值，正则化项则使用L0范数作为平滑—稀疏约束。

4.1 数据项优化

为了优化数据项，在原数据项中引入一度量输出(u，v)与初始光流(u0，v0)之间差异的二次惩罚函数，以保证它们的相似性，即

为了最小化式（31），依据式（32）（33），引入带卷积操作的迭代式，具体为

式中，θ是SOR因子，通常设置为θ= 1。

4.2 正则化处理

为了约束输出光流场(u，v)与(un，vn)之差，考虑如下优化问题

式中，N1和N2分别约束分量u和v的非零梯度数量。通过引入加权系数η，式（38）和（39）可联立为

式（40）采用离散计数方案并以统计方式模拟全局不连续性，传统离散方法（如梯度下降法）难以解决该优化问题。考虑采用间接方法求解并保留模型属性。引入辅助变量p=[pu，pv]T和q=[qu，qv]T并采用二次惩罚函数来度量光流梯度(∇u，∇v)与辅助变量(p，q)之间的差异，可得

式中，λ是比例系数，辅助变量(p，q)与光流梯度(∇u，∇v)之间的相似性可通过λ调节。

为了估计式（41）（42）中的4 个未知量，并最终获得光流场(u，v)，设计了两阶段算法，具体如下：

阶段1）假设u，v已知，求解p与q。

由式（41）（42），有

为方便起见，根据u和v的梯度，令其中一项非负积分为0，则第k次迭代的基本可行解(p，q)为

阶段2）p，q已知。式（41）（42）转化为二次函数最小化问题，即

其离散欧拉—拉格朗日方程可表示为

式中，Δ是拉普拉斯算子，∇·表示散度。采用快速傅里叶变换（fast Fourier transform，FFT）作用于方程两侧，在重新整理排列后可得到光流场计算公式

式 中，F(·)是FFT 算 子，F*表 示F 的 复 合 共 轭，F-1(·)代表逆变换。算法的总体框架如图3所示。

图3 算法总体框架Fig.3 Overview of the proposed method

5 实 验

实验在3 个主流数据集上进行，分别是Middlebury 光流数据集（Baker 等，2011））、KITTI flow 2015光流数据集（Geiger 等，2013）以及MPI Sintel 数据集（Butler 等，2012），以验证光流估计精度，尤其是对光照变化的鲁棒性。实验将本文方法与其他基于全变分框架的光流方法进行比较，并在具有挑战性的KITTI 数据集上与部分基于深度学习框架的光流估计算法进行对比分析。

5.1 基于Middlebury数据集的实验

Middlebury 数据集由两组图像序列组成。训练集仅包含8 对具有ground-truth 的图像对，而测试集是12 对ground-truth 不公开的图像对，以供在线评测。Middlebury 数据集中所有序列的位移都比较小，通常低于10 像素。因此，本文方法可以在不进行空间金字塔运算的情况下对光流估计的准确性进行评估。本文方法的Middlebury 在线评估结果可在网站https：//vision.middlebury.edu/flow/eval/resultsxiaoxin-liao/results-e1.php 查询，本文方法取得了具有竞争力的排名。图4 显示了来自Middlebury 训练集中一些具有复杂纹理图像对的光流可视化结果，从上至下依次是Grove2、RubberWhale、Dimetrodon、Urban2和Venus序列。图4（a）是各序列对应的原始帧，图4（b）是相应的光流场真值，图4（c）是本文方法得到的光流场。从图4 可以看出，本文方法对于包含隐藏纹理的样本同样具有鲁棒性。

图4 Middlebury训练集光流可视化结果Fig.4 Visuallizations of estimated optical flow from Middlebury dataset （（a）original images；（b）ground-truth；（c）ours）

Middlebury 数据集是在稳定光照条件下生成的。为了使用Middlebury 数据集验证模型的光照鲁棒性，考虑对原始图像进行光照合成。

给定与原图像I大小相同的光照核f，则合成光照图像Ir满足

式中，s是图像中像素的2维坐标向量，Q=(1 -ω) +是f的加权核，通过比例参数ω控制光照强度。实验分别采用线性、正弦、高斯和混合高斯的光照模式渲染图像。例如，通过合成第2 帧图像的高斯光照成分使前后帧产生明显光照变化。即

式中，jc表示光照区域的中心，I是原图像，Ir代表渲染结果。提供Guassian 光照核，其高亮显示了原图像中jc中心周围的局部区域。

合成光照实验结果如图5所示。其中，第2列是Middlebury 训练集上RubberWhale 序列第2 帧的合成光照图像，第4—8 列是本文方法和其他4 种常见方法在不同合成光照变化条件下获得的光流场可视化对比结果。从上到下4 行的合成光照模式依次是线性、正弦、高斯和混合高斯（双核）。从图5 可见，在不同光照变化条件下，基于解耦的Wedel 等人（2009）方法和Kumar等人（2013）方法所获光流场严重失真，出现大量噪声，这是由于这两种方法在解耦时无法将光照分量有效分离。而本文方法可通过结构纹理感知方式将光照分量与反射分量充分分离，具有很好的光照鲁棒性，因此可获得最接近于ground-truth 的光流场。此外，基于互相关的SBFlow方法和基于块的WRT 方法虽然也能较准确计算光流，但是会出现零散的噪声，所恢复的运动边缘也存在模糊情况。

图5 合成光照实验结果Fig.5 Optical flow fields from synthtic images with illumination variations （（a）the first frame of RubberWhale sequence；（b）the artificially synthesized image；（c）ground-truth；（d）STARFlow（ours）；（e）Wedel et al.（2009）；（f）WRT；（g）SBFlow；（h）Kumar et al.（2013））

为了得到更客观的比较，图6 给出了在不同光照强度ω取值下这5 种方法在Middlebury 数据集上的平均终点误差（EPE）和平均角度误差（AAE）演变情况。从图6 可见，即使光照变化大（ω取值高），本文方法获得的光流场误差仍然很低且较稳定，这表明STARFlow计算精度高，对光照变化不敏感。

图6 不同光照变化条件下本文方法和其他4种光流估计方法的误差演变情况Fig.6 Error evolution of the proposed method and other four advanced illumination robust optical flow estimation methods under different illumination conditions （（a）linear；（b）sine；（c）Gaussian；（d）mixture of Gaussian）

5.2 基于MPI和KITTI数据集的实验

Middlebury 数据集在分辨率方面具有良好的质量，但该数据集仅包含40 幅合成图像，需要在真实图像序列上进一步评估算法的性能。

MPI Sintel 数据集提供了一个具有挑战性的评估基准。它包含多个具有大位移和镜面反射的真实图像序列。clean和final子集各包含23种不同场景，提供了1 041 个训练图像对和相应的光流场groundtruth。不同光流方法在该数据集上的评估结果如表1 所 示。EPE all（endpoint error over the whole frames）、EPE noc（endpoint error over regions that remain visible in adjacent frames）和EPE occ（endpoint error over regions that are visible only in one of two adjacent frames）分别代表在整个图像、非遮挡区域和遮挡区域计算光流所得的误差。

表1 不同光流方法在MPI Sintel评估数据集上的评估结果Table 1 Evaluation results of different optical flow methods on MPI Sintel dataset

从表1 可以看出，STARFlow 虽然基于变分思想，更适用于小位移序列，但在该数据集下仍然能获得比其他方法更优的估计效果，包括基于深度学习框架的FDFlowNet（fast deep flownet）（Kong 和Yang，2020）和PWC-Net（pyramid，warping，and cost volume net）（Sun 等，2018）方法、基于变分框架的WRT（Mei 等，2020）和SBFlow（Chen 等，2018），以及其他基于图像分解的光流估计方法。

MPI Sintel 数据集的cave 3 序列和Perturbed-Shaman 序列的光流可视化结果如图7 所示。其中，第1 行是MPI Sintel 数据集中的原始图像，第2 行是相应的真实光流场，第3—9 行分别是本文方法（STARFlow）、FDFlowNet、PWC-Net、SBFlow、WRT、Wedel 等 人（2009）的 分 解 方 法 以 及Kumar 等 人（2013）的解耦方法获得的光流场可视化结果。从图7可以看出，基于深度学习框架的FDFlowNet 和PWCNet 以及基于变分框架的WRT 和SBFlow 等方法虽然也能较准确计算光流，但所恢复的运动边缘模糊，缺少了许多运动细节，这表明当前的卷积神经网络（convolutional neural network，CNN）方法不能很好地恢复小尺度运动结构。而本文提出的STARFlow 方法在保留运动细节方面表现更出色，恢复的运动信息更清晰，保持了运动边缘，获得了更接近于ground-truth 的光流场。这得益于L0 正则化器的优势，本文方法在恢复具有高对比度的精细尺度运动结构方面显著优于当前最先进的光流计算方法，如图7 中的红框标记区域，其中流动边缘与groundtruth更加接近。

图7 MPI Sintel数据集光流可视化结果Fig.7 Visualizations of estimated optical flow fields from MPI Sintel dataset（（a）Cave 3 in clean set；（b）Cave 3 in final set；（c）Perturbed-Shaman in clean set；（d）Perturbed-Shaman in final set）

KITTI flow 2015数据集由194组图像序列构成，这些图像序列获取自一辆行驶中的车辆。该车辆配备了精确的测距仪，并对其自身运动进行精确定位，通过特定方法获得真实光流场。与MPI Sintel 数据集相似，KITTI 数据集包含了大量大位移运动，如快速行驶的车辆。通过在该数据集上的实验，同时与其他方法进行比较（其中大部分是基于深度学习的光流估计方法），本文方法（STARFlow）在Fl-bg（the percentage of flow outliers averaged over background regions）、Fl-fg（the percentage of flow outliers averaged over foreground）和Fl-all（the percentage of flow outliers averaged over all regions）3 个指标上相比于其他方法具有明显优势，如表2 所示。同时，图8 给出了不同光流方法在KITTI 评估集image_2 序列上获得的彩色编码光流图像及其误差图。误差图使用对数色标，正确估计和错误估计分别用蓝色和红色阴影表示，暗色调代表位于图像区域之外的被遮挡像素。结果表明，在各种具有挑战性的细节（如移动的车辆、路灯和建筑物等）中，相比于其他方法，STARFlow在保留运动细节方面表现更优，误差图中蓝色阴影更多而红色阴影更少，表明本文方法能更清晰地恢复运动特征，更多的运动边缘得到保持。KITTI数据集本身含有强光照变化，STARFlow 光流估计结果更接近于真实光流场，说明该方法精度高，鲁棒性强。

图8 不同方法在KITTI数据集上的光流图和误差图Fig.8 The estimated optical flow and error maps of different methods on KITTI dataset（（a）the 0000016 sequence in image2 set；（b）the 0000008 sequence in image2 set）

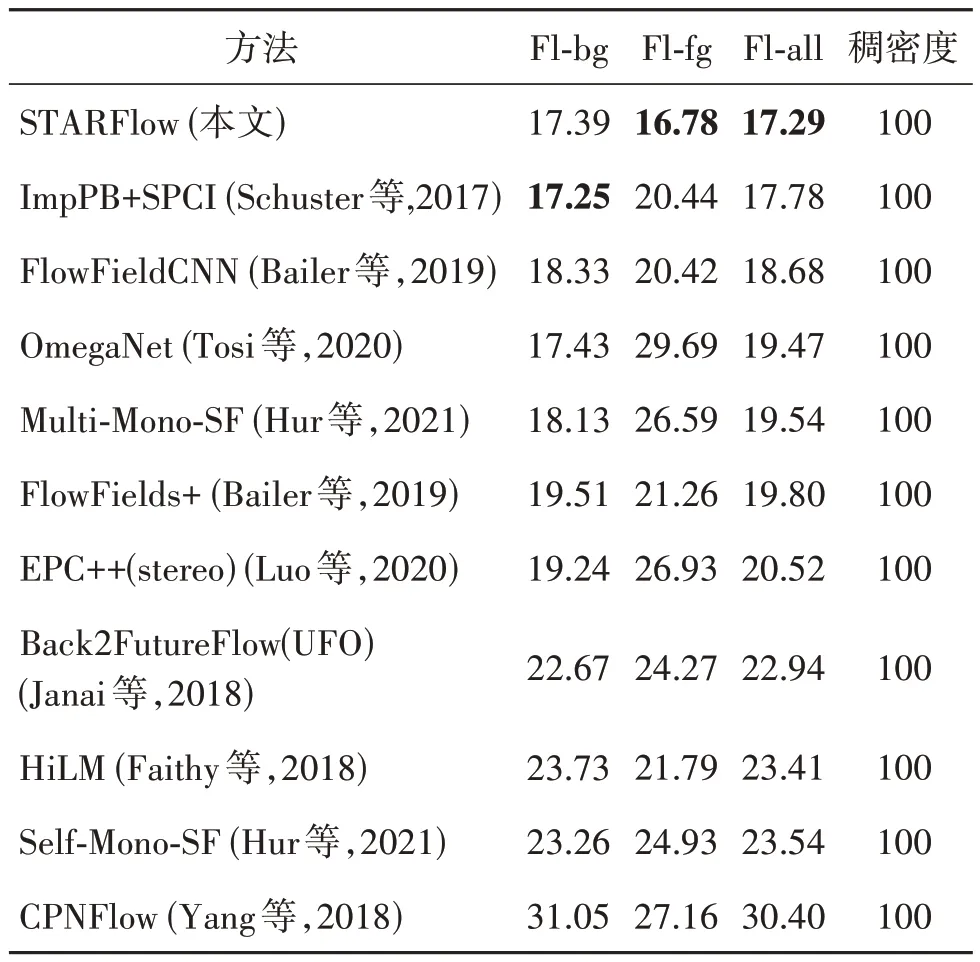
表2 不同光流方法在KITTI flow 2015评估数据集上的评估结果Table 2 Evaluation results of different optical flow methods on KITTI flow 2015 evaluation dataset/%

总之，尽管本文方法更适合于小位移运动恢复，但在Middlebury、MPI Sintel 和KITTI flow 2015 等具有挑战性的评测基准上均实现了高精度的光流估计。值得注意的是，尽管MPI Sintel 和KITTI 数据集中包含复杂光照变化，STARFlow 方法仍能取得鲁棒的光流估计结果。

6 STARFlow在人脸活体检测上的应用

为了验证STARFlow 光流方法在实际应用方面的有效性，本文将提取的光流特征在CASIA 人脸反欺骗数据集（Zhang 等，2012）上进行人脸活性检测实验。CASIA 数据集包含真实人脸和欺骗人脸的视频片段，这些片段具有许多复杂的欺骗模式，也包含较多的大位移，这对基于变分的光流方法是相当具有挑战性的。为了验证本文方法的光照鲁棒性，在数据集中添加了4 种不同的合成光照。此外，将STARFlow 光流方法与最先进的基于光流的反欺骗方法进行比较。例如，CASIA 团队的方法（CASIA）（Chingovska 等，2013）、基于深度网络的无监督光流方法ARFlow（Liu 等，2020a）、基于变分的光流计算方法WRT（Mei 等，2020）和SBFlow（Chen 等，2018）。实验统计了每种方法的反欺骗分类准确率和半总错误率（half total error rate，HTER）。HTER 是一类评判活体检测算法性能的重要标准，指的是错误拒绝率（false rejection rate，FRR）和错误接受率（false acceptance rate，FAR）总和的一半。反欺骗分类准确率和半总错误率的比较结果如表3 和表4 所示。其中，平均正确率表示在4 种合成光照条件下的准确率和半总错误率的平均值；平均变化表示不同光流方法在原数据集下的准确率和HTER 与平均值Average之差。

从表3 和表4 可以看出，本文方法比ARFlow，SBFlow，WRT，CASIA方法均具有更高的分类准确率和更低的半总错误率。在原数据集下分别提高了约3.5%，4.2%，4.4%，9.1%。与其他光流方法相比，STARFlow 光流方法在不同光照变化情况下的准确率和半总错误率也表现得更加稳定。与无光照变化情况相比，STARFlow 光流方法的准确率和半总错误率平均变化分别为1.1%和1.6%，明显优于其他方法。实验结果进一步验证了STARFlow 光流方法在不同光照变化下具有良好的鲁棒性，更适合于人脸活性检测应用。

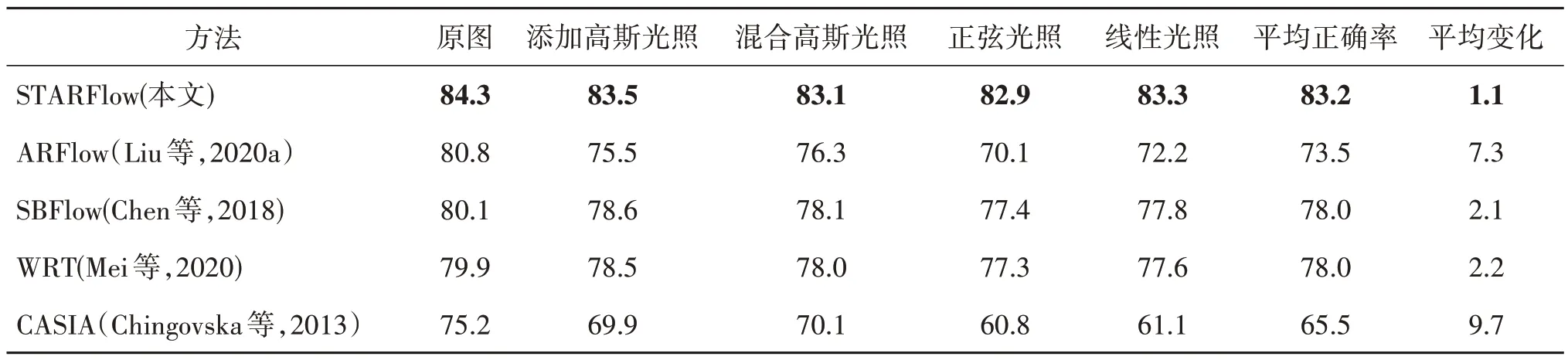
表3 在CASIA数据集上进行人脸活性检测的准确率对比Table 3 The accuracy of face liveness detection on the CASIA dataset under different illumination patterns/%

表4 在CASIA数据集上进行人脸活性检测的半总错误率对比Table 4 The HTER of face liveness detection on the CASIA dataset under different illumination patterns/%

7 结 论

本文提出了一种基于STAR 解耦的鲁棒光流估计方法，基于结构纹理感知Retinex 模型，将图像中的光照与反射分量分离。为了在计算光流时保持良好的运动边缘，使用L0 梯度最小化对光流场进行平滑处理，稀疏约束限制了速度与扩散梯度的非零个数。此外，给出了求解优化问题的数值办法。最后，在3 个具有挑战性的光流数据集上进行评估，验证了STARFlow 方法的计算精度与光照鲁棒性。将STARFlow 方法应用于脸部运动光流特征提取并进行人脸活体检测实验，对比实验验证了STARFlow方法更具鲁棒性，改善了人脸活体检测效果。在下一步工作中，将致力于提升本文方法的实时性能并将应用于生物特征识别、机器视觉等领域。