基于树莓派的高效卷积优化方法

郭晓龙,牛晋宇,杜永萍

(北京工业大学 信息学部,北京 100124)

0 引 言

随着深度学习的快速普及,卷积神经网络在图像识别、目标跟踪等视觉领域作为其算法的核心技术得到了广泛应用。通常卷积操作无论在参数量大小还是运算复杂度上已经占据了整个模型的80%以上。尤其针对低功耗等边缘设备,受其有限的算力和内存宽带资源的限制,能否在此类设备上落地应用成为亟需解决的优化问题。虽然各大厂商都推出了自己的推理框架,如Caffe、TensorFlow Lite、ncnn、mnn等,但是这些框架通常作为通用型推理框架,往往在某一特定平台(比如树莓派)下未必能够达到速度最优。比如Caffe使用Im2col技术做卷积优化,其核心思想是将卷积操作转化为两个矩阵相乘,为实现直接矩阵乘法,先要将输入数据和卷积核按照卷积规则在内存中重新排布变成二维矩阵。但在树莓派上其内存重排的耗时往往要大于直接卷积的耗时,还未包含后面的矩阵乘法运算耗时。此外还有国内的开源推理框架ncnn,针对卷积的padding操作也需要提前做内存重排,以及卷积的bias和relu操作也需要重新遍历一遍内存。可见其昂贵的额外访存开销变成了资源的额外浪费。

1 计算图优化

计算图优化[1]的作用是在不影响模型数值精度的基础上,通过拓扑图变化达到减化计算、减少访问等系统开销的目的,有助于特定设备推理加速。在推理过程中,对于不断的图片检测输入,计算图优化部分只需要在前期做一次即可,后期的每一次推理都可以直接使用优化结果。因此,图优化是整个推理框架[2]的首要准备及重要工作,也是收益最大的一部分。

1.1 算子融合

该文优化的模型为Retinaface[3],该模型基于MobileNet网络架构[4]。其中类似Conv+BN+ReLU的经典组合占据了模型的80%以上。为提升推理速度,可以采用算子融合的方法将3个算子变为1个算子,从而减少计算量和访存量。首先,Conv和BN进行合并的推导公式可以参考文献[5],提前把卷积新的Weight和Bias计算好,替换原卷积对应的Weight和Bias值,同时删除BN算子。其次,对于Relu算子,可以采用本地合并计算(inplace relu)方法,就是在卷积运算的类中设置标志bool relu,在卷积计算之后结果写到内存之前,根据保存的relu标志位来决定是否执行std::max(x,0)。由此优化掉了一次全局内存遍历。最终如图1所示。

图1 Conv+BN+ReLU算子融合

1.2 算子布局优化

为了充分利用CPU计算硬件特性,该文采用NEON SIMD方式进行计算加速。树莓派4B采用的ARM A72 64位CPU,NEON指令宽度是128 bit,即16字节,而float占4个字节,因此一条NEON指令可以处理4个float数据。又根据卷积的运算公式是卷积核与图像数据的对应位置相乘再相加到结果中,因此与NEON中的FMLA指令的处理方式相同。基于此,该文采用一种名为NHW4C的存储形式,将同一像素的连续的4通道像素连续存储在一起。每4通道所有W*H数据组成一组,一共分成C/4组。

2 卷积优化方法

经过上一步的计算图优化之后,已经合并了所有的BN+ReLU算子,拓扑图已经变成连续相邻的卷积算子,且所有卷积算子的Weight和Bias参数格式已转换为NHW4C。为了评估卷积的优化方法[6],该文采用Roofline模型分析方法。

Roofline模型[7]分析方法使用计算强度(Operational Intensity)进行定量分析,并给出了模型在计算平台上所能达到理论计算性能上限的公式。公式表达为算力上限π除以带宽上限β,两个指标相除即可得到计算平台的计算强度上限Imax,单位是FLOPs/Byte。树莓派4B的峰值算力π=1.5 GHz*1(FMLA指令为单发射)*(4+4)(FMLA指令一次可以完成4次加法和4次乘法)=12G Flops/s。内存带宽β=4G Bytes/s。因此树莓派4B的理论计算强度Imax上限=12/4=3 FLOPs/Byte(这里计算的值均为理论值,实测可能要稍低一点)。若计算出的强度低于3 FLOPs/Byte为带宽瓶颈区域,说明因为访存过大无法完全发挥平台算力。高于3 FLOPs/Byte为计算瓶颈区域,说明此时算法已经100%地利用了CPU的全部算力。该文的优化目标就是尽量接近Imax理论上限。树莓派4B的理论计算强度如图2所示。

图2 树莓派4B Roofline模型

2.1 3×3普通卷积

Retinaface模型的第一个算子就是3×3普通卷积,输入tensor为(1,IC,IW,IH),输出tensor为(1,OC,OW,OH),卷积核tensor为(OC,IC,3,3),输入通道IC=3,输出通道OC=8,步长stride =2。算法1给出了一个普通卷积的常规计算方法。

算法1:3×3普通卷积原始算法。

输入:input tensorI,kernel filterF,paddingP,strideS;

输出:output tensorO。

1 Mat IP=enlarge inputIwith paddingP

2O=add(O,bias)

3 forc=0 toCo-1 do

4 forw=0 toWo-1 do

5 forh=0 toHo-1 do

6 fork=0 toCi-1 do

7 fori=0 toWf-1 do

8 forj=0 toHf-1 do

9Oc,w,h+=IPk,w×s+i,h×s+j×Fc,k,i,j

10O=max(0.f,O)

算法1流程与ncnn中卷积算法基本一致,除了卷积计算部分(第3～9行)采用SIMD外。算法1对内存的所有操作包括:

(1)对输入数据进行padding扩张。读取输入数据后写入到扩张的新内存。共需要IC*IW*IH+IC*(IW+2*padding)*(IH+2*padding)内存读写。可省略为2*IC*IW*IH。

(2)将bias值提前写到输出数据中(第2行)。共需要OC*OW*OH内存读写。最后对输出数据进行Relu操作(第10行),先读取后写入,共2*OC*OW*OH。

(3)4层for循环中(第3～6行)输入数据共读取了OC*IC*IW*IH,输出数据先读取后写入总量2*OC*IC*OW*OH。

(4)卷积核共需OC*IC*3*3内存读取。

算法1的计算访存比为:

[OC*IC*OW*OH*3(KW)*3(KH)*2]/

[((2+OC)*IC*IW*IH+5*OC*IC*OW*OH+OC*IC*3*3)*sizeof(float)]

由 IC=3,OC=8,stride=2,可知OW=IW/2,OH=IH/2。因此可以进一步简化为:

可见算法1的计算强度仅为树莓派4B的理论计算强度的15%。已经明显属于严重访存瓶颈区域了,严重受限于访存瓶颈的限制,无法发挥硬件的算力。

2.1.1 访存优化

由于第一个算子的输入数据(Input Tensor)是每一次推理过程的外部传入的(通常为图像的RGB输入格式),其格式为NCHW,这里也可以将NCHW转为NHW4C再进行推理(如ppl.nn框架就是这么做的)。但即使输入数据尺寸为320*320,3通道的float类型图片数据,占用内存空间也达到了1 200 KB,在树莓派4B上一次Reorder转换耗时就要3 ms,一次padding扩张需要2 ms。尺寸为800*800的Reorder转换耗时高达18 ms,padding扩张也高达12 ms。所以进行一次内存格式转换是非常昂贵的。因此,算法2采用直接卷积方法,意味着输入数据为NCHW,卷积核和输出数据为NHW4C。同时对于算法1中第1行代码的padding操作,也采用9宫格分块的策略进行优化。该文提出的算法2总体的优化思路是减少所有不必要的访存开销。

算法2:3×3普通卷积优化算法。

输入:input tensorI,kernel filterF,biasB,paddingP,strideS;

输出:output tensorO。

1 out_neon_w_start=(left_padding+s-1)/s;

2 out_neon_h_start=(top_padding+s-1)/s;

3 out_neon_h_end=Ho-bottom_padding/s;

4 out_neon_w=(out_neon_w_end - out_neon_w_start)>>2

5 out_left_start=out_neon_w_start+out_neon_w<<2

6 out_left_w=Wo-out_left_start

7 for oc=0 toCo/4-1 in parallel do

8 for ic=0 toCi-1 do

9 fori=0 toWfdo

10 forj=0 toHfdo

11Ki,j=SIMD_Load(Foc,ic,i,j)

12 out_bias=(ic==0) ? Boc:0

13 relu0=((ic==Ci-1) &&relu_flag) ? 0:-max_float

14 for top=0 to out_neon_h_start-1 do

15 direct_padding(Iic, -left_padding, top×s-top_padding,Ooc,0,top,K,Wo,out_bias,relu0)

16 for top=out_neon_h_start to out_neon_h_end-1 do

17 direct_padding(Iic, -left_padding, top×s-top_padding,Ooc,0,top,K,output_neon_w_start,out_bias,relu0)

18 direct_padding(Iic,out_left_start×s-left_padding, top×s-top_padding, Ooc,out_left_start,top,K,out_left_w,out_bias,relu0)

19 for top=out_neon_h_start to (out_neon_h_end-1)/2 step 2 do

20 direct_simd(Iic,out_neon_w_start×s-left_padding, top×s-top_padding,Ooc,out_neon_w_start,top,K,out_neon_w, out_bias, relu0)

21 for top=out_neon_h_end toHo-1 do

22 direct_padding(Iic, -left_padding, top×s-top_padding,Ooc,0,top,K,Wo, out_bias, relu0)

23 Function direct_padding(IB,OB,K,ow,bias,relu0):

24 forw=0 to ow-1 do

25v=SIMD_fadd(SIMD_Load(OBw×4),bias)

26 fori=0 toWfdo

27 forj=0 toHfdo

28 if not in padding:

29 SIMD_fma_lane(v,Ki,j,IBw×s+i,j,i)

30v=SIMD_fmax(v,relu0)

31 SIMD_Store(OBw×4,v)

32 Function direct_simd(IB,OB,K,ow,bias, relu0):

33 forw=0 to ow -1 do

34 fork=0 to 3 do

35Vk=SIMD_fadd(SIMD_Load(OB(w×4+k)×4, 0), bias)

36Wk=SIMD_fadd(SIMD_Load(OB(w×4+k)×4, 1), bias)

37 fori=0 to Wfdo

38 forj=0 to Hfdo

39 fork=0 to 3 do

40 SIMD_fmla(Vk,Ki,j, IB(w×4+k) ×s+i, j)

41 SIMD_fmla(Wk,Ki,j, IB(w×4+k) ×s+i, j+s)

42 fork=0 to 3 do

43Vk=SIMD_fmax(Vk, relu0)

44Wk=SIMD_fmax(Wk, relu0)

45 SIMD_Store(OB(w×4+k)×4, 0,Vk)

46 SIMD_Store(OB(w×4+k)×4, 1,Wk)

9宫格分块策略。为了避免对输入数据进行padding的扩张,提出了一种9宫格的分块策略,如图3所示。9宫格的思想是建立一个虚拟的padding区域(虚线框),而实际的输入数据尺度是不变的(实线框)。之所以这样建立,是因为padding区域填充的元素都为0,而输入数据的0乘以任何卷积核元素都为0。例如图3中白底的卷积框所对应的卷积结果=k1*i1+k2*i2+k3*i3+k4*i4+k5*i5+k6*i6+k7*i7+k8*i8+k9*i9。其中k1/k2/k3/k4/k7所在区域为padding,所有值全为0。因此只需要计算非padding区域即可,最后简化为:k5*i5+k6*i6+k8*i8+k9*i9。这就是算法2中direct_padding函数所实现的功能。同理,算法只需对所有卷积核落在虚线框的padding区域中(即9宫格的外圈8格)统一调用direct_padding函数做特殊处理。那么剩下的中间input区域都是有效区域,卷积核的所有元素都可参与运算(如黑底的卷积框),就可以利用SIMD进行加速处理。9宫格的分块策略虽然增加了一些算法复杂度,但是节省了一次全量内存拷贝,相比于昂贵的内存开销,所增加的逻辑处理耗时要小的多。但是这里有一点需要注意的地方是,对于padding区域地址的计算会产生内存溢出,如算法2第15行对输入数据的地址计算,它指向了外侧虚线框的起始位置。这样使用主要是为了地址计算的统一性,只要提前判断,溢出的地址不访问,就不会报错(即便是内存泄露工具检测也不会报错)。

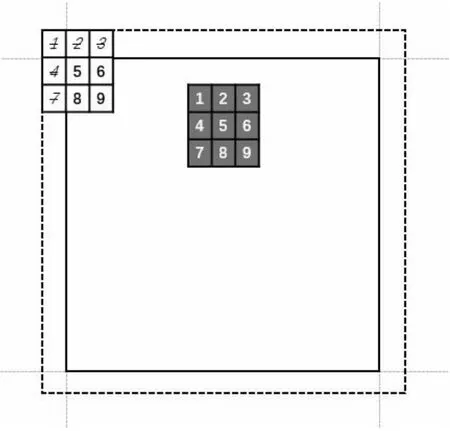
图3 卷积计算的padding策略

访存合并。此外Add bias的处理也可以优化到算法逻辑中,因为每一层的输出数据都是所有输入数据的全部channel层的卷积求和。因此,该文的做法是在每一次对输入数据channel的遍历都强制加上out_bias,只不过这里的bias只有在input channel第一层的时候才是真的bias参数,其他层为0。这么做的目的是为了指令流水线不被if指令中断,因为CPU的分支预测如果发生错误,就需要清空流水线,重新加载正确的分支,会产生Pipeline Bubbles,相对成本较高。而多加的一条SIMD_fadd指令最多只消耗4个时钟周期,而且吞吐量为2条,即4个时钟周期可以同时处理两条fadd相加指令。最后Relu的处理也类似,是在input channel最后一层,因为最后一层的卷积结果与前面所有层相加之后才是最终输出结果。因此,只有最后一层,relu0的值才为0,其他情况是float负数较大值,故SIMD_fmax只有relu=0时才会生效。SIMD_fmax指令延迟3个周期,吞吐量2条。

算法2中对内存的所有操作包括:

(1)由于输出数据和卷积核都采用了NHWC4格式(输入数据仍为NCHW),每次可以利用SIMD同时处理4个channel,因此最外层循环次数降为OC/4,所以输入数据读取降到了OC/4*IC*IW*IH。

(2)9宫格分块策略只是分开读取,但读取总量不变,因此输出数据先读取后写入总量为2*OC/4*IC*OW*OH*4。

(3)卷积核共需OC/4*IC*3*3*4内存读取。

算法2的计算访存比为:

[OC*IC*OW*OH*3(KW)*3(KH)*2]/

[(OC/4*IC*IW*IH+2*OC*IC*OW*OH+OC*IC*3*3)*sizeof(float)]

进一步简化为:

最终算法2的计算强度相当于算法1提升了3倍,相当于树莓派4B的理论一半。加上NEON指令的加持,推理速度得到大幅改进。

2.1.2 SIMD指令优化

使用SIMD指令计算量不变,只是利用ARM NEON指令一次可以处理4个float的乘加操作[8],提升计算速度,所以Roofline模型中算力上限π是不变的。SIMD的优化方法分为二部分:其一是padding区域的处理,这里使用了NEON Intrinsics函数,每次处理1个元素的4个通道卷积结果(如direct_padding函数)。其二是非padding区域的处理,这里使用了Asm Volatile内联汇编方式,每次处理8个元素的4个通道卷积结果(如direct_simd函数)。

根据Cortex A72优化手册,LD1指令,一次可以读取4个float,指令延时(Exec Latency)为5个时钟周期,吞吐量(Execution Throughput)为1,每时钟只能发射1条LD1指令。FMLA指令,一次针对4个float(Q-form)进行乘加操作,指令延时为7个时钟周期,每时钟只能发射一条FMLA指令。但LD1和FMLA所使用的执行端口(Utilized Pipelines)不同,这意味着对于数据无关的二条指令是可以并行执行的,如图4所示。

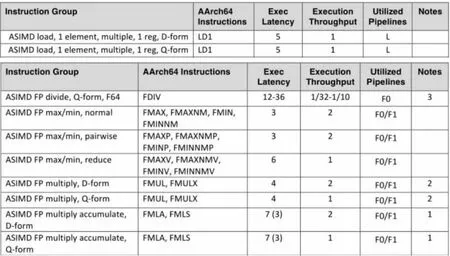
图4 Cortex A72优化手册

根据A72优化手册[9],一条读取指令LD1的耗时比FMLA少了2个时钟周期,意味着一条FMLA指令就可以遮盖LD1取数据的耗时,因此只要流水线设计合理,就不会使得LD指令变成瓶颈,运算器才不会因等待而浪费。鉴于FMLA指令的延迟为7周期,每周期吞吐量为1,因此最少需要7条无数据写依赖关系(读依赖不影响)的FMLA指令才能填满流水线。根据上述结论,算法设计为每次迭代输出2行,每行4个像素,共需要8条FMLA指令。一条FMLA指令可处理4个float,因此每次迭代共输出32个卷积中间结果。图5所示为stride=2的单次迭代卷积所有参数个数。

图5 3×3普通卷积单次迭代示意图

指令流水线设计。图5所示的输入数据格式是NCHW,卷积核Weight、Bias以及输出数据格式为NHW4C。为了避免Reorder操作,一条FMLA指令计算方法是将输入数据的1个元素分别与卷积核的1个元素4通道(同色块)相乘,结果与输出数据的1个元素4通道(同色块)相加。同理分别对卷积核的9个元素遍历运算,将每次运算结果产生的8*4个float输出数据求和累加,就得到了单通道输入图像的卷积结果(算法2第37～41行)。其中8*4个float输出数据是存放在neon寄存器中的,所以累加求和的操作并不会每次都要访存。故将算法分成了9组,每组有连续的8条不存在写依赖关系的FMLA指令,对输入数据的LOAD指令可以穿插在每组中间,而卷积核的9条LD指令在调用函数前就加载到neon寄存器中了。按此设计就可以充分发挥处理器流水线作业。同理,遍历输入数据的所有3个通道,将所有输出通道的卷积结果累加就完成了3×3普通卷积最终结果。这就是算法2中,函数direct_simd所实现的功能。

循环展开优化。实际编写代码除函数内第1行循环(第33行代码)外,direct_simd函数中的其他for循环都是不存在的。算法2中这样写是为了避免占用过长的篇幅。实际上for循环属于分支预测指令,如果预测失败,同样会导致清空流水线,重新加载正确的分支。因此,为了保证流水线不会产生气泡,direct_simd里第34行到第46行代码都是展开的,这种方法叫作循环展开优化[10]。

2.2 逐通道卷积(Depthwise Conv)

Mobilenet中逐通道卷积尺寸通常为:输入tensor为(1,C,IW,IH),输出tensor为(1,C,OW,OH),卷积核tensor为(1,C,3,3)。所有tensor的通道数是一致的。因为卷积运算只关心当前通道,因此不需要遍历输入层和卷积核的所有通道[11],所以相比于3×3普通卷积和逐点卷积访存效率要高得多。未优化版本如算法3所示。

算法3:逐通道卷积原始算法。

输入:input tensorI,kernel filterF,paddingP;

输出:output tensorO。

1 Mat IP=enlarge inputIwith paddingP

2O=add(O,bias)

3 forc=0 toC-1 do

4 forw=0 toWo-1 do

5 forh=0 toHo-1 do

6 fori=0 toWf-1 do

7 forj=0 toHf-1 do

8 Oc,w,h+= IPc,w+i,h+j×Fc,i,j

9O=max(0,f,O)

整体流程与算法1基本一致,只是中间少了一层对输入层通道的遍历。算法3中对内存的所有操作包括:

(1)对输入数据进行padding扩张约为2*C*IW*IH。

(2)Addbias:C*OW*OH。Relu操作:2*C*OW*OH。

(3)输入数据读取C*IW*IH,输出数据读写2*C*OW*OH。

(4)卷积核共需C*3*3内存读取。

算法3的计算访存比为:

[C*OW*OH*3(KW)*3(KH)*2]/[(3*C*

IW*IH+5*C*OW*OH+C*3*3)*sizeof (float)]

由stride =1,OW=IW,OH=IH,则进一步简化为:

同样算法3,也是严重访存瓶颈区域了,严重受限于访存瓶颈的限制。远远无法达到树莓派4B的理论上限3 FLOPs/Byte。

2.2.1 访存优化

与3×3普通卷积算法的优化方法相同,减少所有不必要的访存开销。同样采用9宫格分块策略和访存合并。因此,该文提出的逐通道卷积优化方法,如算法4所示。

算法4:逐通道卷积优化算法。

输入:input tensorI,kernel filterF,biasB;

输出:output tensorO。

1 Function depthwise_simd(IB,OB,K,ow,bias,relu0):

2 forw=0 to ow-1 do

3 fork=0 to 3 do

4Vk=SIMD_fadd(SIMD_Load(OB(w×4+k)×4,0), bias)

5Wk= SIMD_fadd(SIMD_Load(OB(w×4+k)×4, 1), bias)

6 fori=0 toWfdo

7 forj=0 toHfdo

8 fork=0 to 3 do

9 SIMD_fmla(Vk,Ki,j,SIMD_Load(IB(w×4+k)×4+i, j))

10 SIMD_fmla(Wk,Ki,j,SIMD_Load(IB(w×4+k)×4+i, j+1))

11 fork=0 to 3 do

12Vk=SIMD_fmax(Vk,relu0)

13Wk=SIMD_fmax(Wk,relu0)

14 SIMD_Store(OB(w×4+k)×4, 0,Vk)

15 SIMD_Store(OB(w×4+k)×4, 1,Wk)

Depthwise卷积对padding的处理同样采用9宫格分块策略,与算法2相同,这里就不重新列出了。

算法4中对内存的所有操作包括:

(1)输入数据读取为C/4*IW*IH。

(2)输出数据读写总量为2*C/4*OW*OH*4。

(3)卷积核共需C/4*3*3*4内存读取。

算法4的计算访存比为:

[C*OW*OH*3(KW)*3(KH)*2]/[(C/4*

IW*IH+2*C*OW*OH+C*3*3)* sizeof(float)]

由stride =1,OW=IW,OH=IH,则进一步简化为:

最终算法4的强度接近于树莓派4B的理论2/3。比优化前提升了3.5倍。

2.2.2 SIMD指令优化

指令流水线设计。与3×3普通卷积需要遍历二层(OC/4、IC)通道相比,逐通道卷积只需遍历一层(C/4)通道。另外,由于3×3普通卷积每次只能处理1个输入元素的1通道,而NHW4C格式的输入数据每次卷积运算就可以处理1个输入元素的4通道。可见仅靠NHW4C格式,就能将处理能力提升4倍。首先,为保证最少7条无数据写依赖关系的FMLA指令来填满流水线,算法设计为每次迭代输出2行,每行4个像素,共需要8条FMLA指令。其次,因卷积核大小为3*3,需要分别对卷积核的9元素运算,故分成了9组,每组有连续的8条FMLA执令,LD指令可以穿插在每组中间。每次迭代共输出32个卷积最终结果,如图6所示。

图6 逐通道卷积单次迭代示意图

循环展开优化。同样为了避免占用过长的篇幅,实际编写代码除函数内第1行循环(第3行代码)外,depthwise_simd函数中的其他for循环都是不存在的。采用循环展开优化技术,从而避免了分支预测指令和流水线产生气泡。

2.3 逐点卷积

Mobilenet中逐点卷积尺寸通常为:输入tensor为(1,IC,IW,IH),输出tensor为(1,OC,OW,OH),卷积核tensor为(OC,IC,1,1)。未优化版本如算法5所示。

算法5:逐点卷积原始算法。

输入:input tensorI,kernel filterF;

输出:output tensorO。

1O=add(O,bias)

2 forc=0 toCo-1 do

3 forw=0 toWo-1 do

4 forh=0 toHo-1 do

5 fork=0 toCi-1 do

6Oc,w,h+=IPk,w,h×Fc,k

7O=max(0.f,O)

算法5中对内存的所有操作包括:

(1)Add bias:OC*OW*OH。Relu操作:2*OC*OW*OH。

(2)输入读取OC*IC*IW*IH,输出读写2*OC*IC*OW*OH。

(3)卷积核共需OC*IC*1*1内存读取。

算法5的计算访存比为:

[OC*IC*OW*OH*1(KW)*1(KH)*2]/

[(OC*IC*IW*IH+2*(1+IC)*OC*OW*OH+OC*IC*1*1)*sizeof(float)]

由padding=0,stride =1,OW=IW,OH=IH,IC通常在8～256之间,则进一步简化为:

逐点卷积的计算强度为树莓派4B的理论的5.6%。

2.3.1 访存优化

对于1×1卷积,TensorFlow Lite[12]的做法是转换成二个矩阵的乘法[13-14],然后使用OpenBLAS高性能矩阵乘法库[15]来完成卷积运算。而该文由于采用NHW4C格式,转换成两个矩阵乘法的格式内存开销较大。因此,逐点卷积优化方法与之前相同,减少所有不必要的访存开销。优化如算法6所示。

算法6:逐点卷积优化算法。

输入:input tensorI,kernel filterF,biasB;

输出:output tensorO。

1 for oc=0 toCo/4-1 in parallel do

2 for ic=0 toCi/4-1 do

3 out_bias=(ic==0) ?Boc: 0

4 relu0=((ic==Ci-1) &&relu_flag) ? 0:-max_float

5 forn=0 to 3 do

6Kn=SIMD_Load(Foc,ic,n*4)

7 forw=0 to (Wo*Ho)/8-1 do

8 fork=0 to 7 do

9Vk=SIMD_fadd(SIMD_Load(Ooc,(w×8+k)×4), bias)

10Xk=SIMD_Load(Iic,(w×8+k)×4)

11 forn=0 to 3 do

12 fork=0 to 7 do

13 SIMD_fmla(Vk,Kn,Xk[n])

14 fork=0 to 7 do

15Vk=SIMD_fmax(Vk, relu0)

16 SIMD_Store(Ooc,(w×8+k)×4,Vk)

逐点卷积没有padding参数,因此不需要9宫格分块策略。算法6中对内存的所有操作包括:

(1)输入数据读取为OC/4*IC/4*IW*IH*4。

(2)输出数据读写总量为2* OC/4*IC/4*OW*OH*4。

(3)卷积核共需OC/4*IC/4*1*1*4*4内存读取。

算法6的计算访存比为:

[OC*IC*OW*OH*1(KW)*1(KH)*2]/

[(OC/4*IC*IW*IH+OC/2*IC*OW*OH+OC*IC*1*1)*sizeof(float)]

由stride =1,OW=IW,OH=IH则进一步简化为:

优化后的计算强度也仅为理论的22%,与逐通道卷积相差很大。从最终实验也知,逐点卷积效率是三者中最差的。

2.3.2 SIMD指令优化

由于逐点卷积的卷积核大小是1*1的,卷积操作每次只需要一个输入元素。所以输入/输出Tensor由宽和高组成的二维数组可以看成连续排列的一维数组,且输入和输出数据的一维数组长度相等,同时输入/输出的格式都是NHW4C。逐点卷积的设计原则依然是组成8条FMLA指令流水线,因此算法6中单次迭代(第7～16行)可以对8个输出变量进行1×1卷积运算,如图7所示。

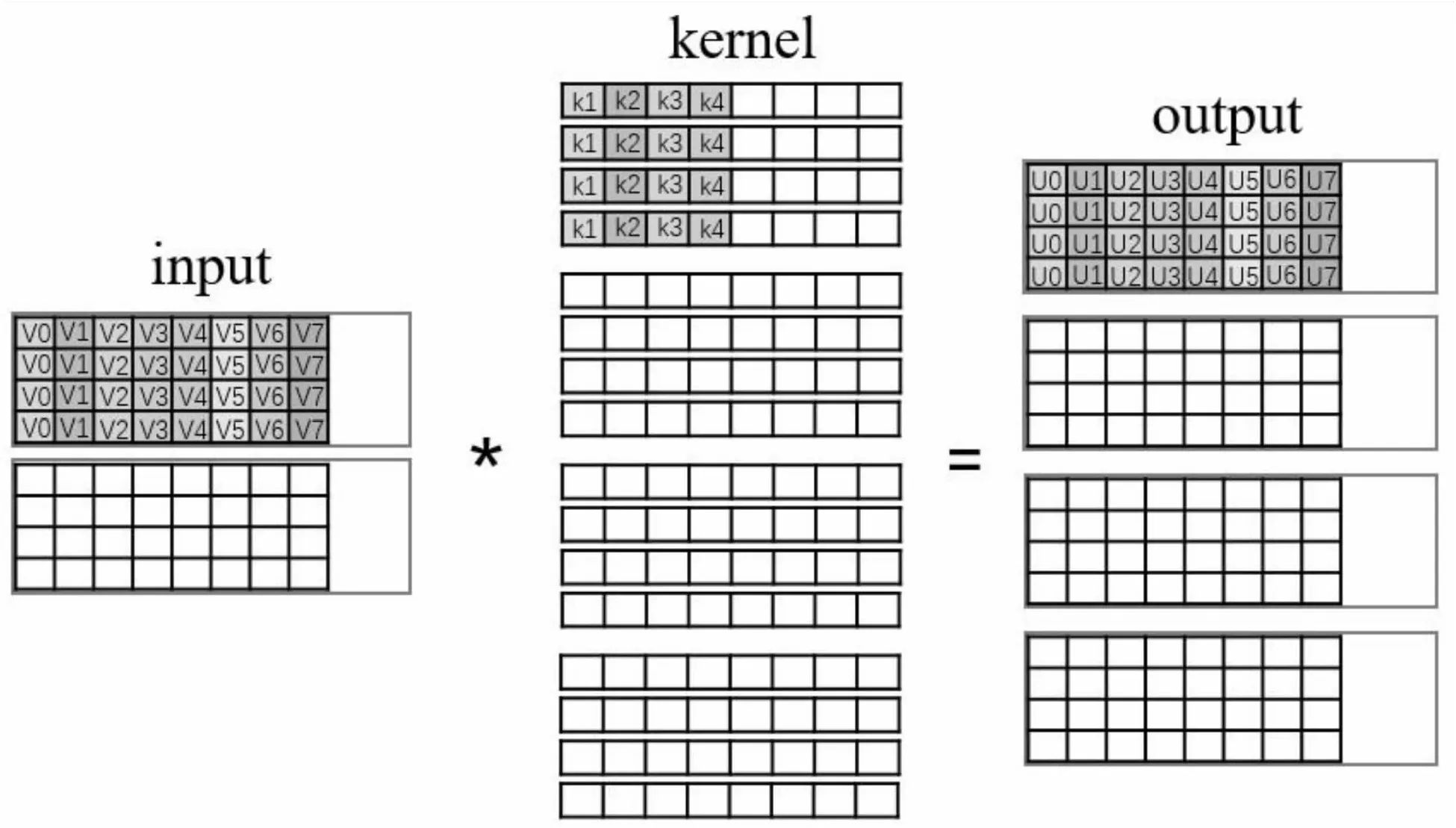
图7 逐点卷积单次迭代示意图

指令流水线设计。图7所示逐点卷积所有参数的例子,图的左侧是输入Tensor(1,8,W,H),中间卷积核Tensor (16,8,1,1),右侧输出Tensor(1,16,W,H)。其中输入数据和输出数据可以看成一维数组,长度为W*H,NHW4C格式由4个连续通道数据排列在一起,因此输入Tensor分成了上下两组(8/4),输出Tensor分成了四组(16/4)。卷积核大小为16*8个,同样分成了4组,每组中又分成2组(与输入数据通道数相对应)。算法的设计思想是,对于每一组的输出数据是所有组的输入数据卷积后累加求和而得(第2～16行代码)。为求得一个输出元素的4通道数据U0,需要对每组的输入数据分别用每一通道与1个卷积核4通道相乘,产生的4条FMLA指令结果累加而成。如:①U0=k1*V0[0]②U0+=k2*V0[1]③U0+=k3*V0[2]④U0+=k4*V0[3]。由于这4条FMLA指令存在写依赖关系,因此同时处理8个输出元素U0～U7,将上述4步的每一步分散在8个输出元素中,从而组成8条无写依赖的FMLA指令(第11～13行)。对于不满8条的剩余输入/输出数据,可以利用NEON Intrinsics函数,采用同样方法,每次可处理1个元素的4通道卷积。

循环展开优化。同样代码中第5～14行的所有for循环需要展开处理,与前面方法相同不再重复。

3 实验结果

测试平台为:树莓派4B 4 GB内存,Raspberry Pi OS 64位系统,Retinaface mnet 0.25模型。该文提出的三种算法分别与国产开源框架腾讯ncnn、商汤ppl.nn及阿里mnn做对比。分别测试三种不同分辨率图片在不同平台耗时。测试方法使用源码Release编译,开启OpenMP及O2编译优化选项,并在源码中添加耗时打印语句。注:这里统计的耗时不包含图优化部分,只有每一层的算子推理耗时。具体如表1～表3所示。

表1 3×3普通卷积耗时分析 ms

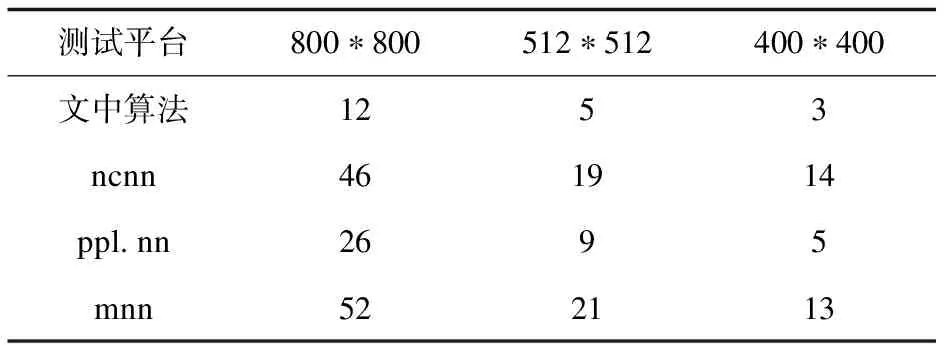
表2 逐通道卷积耗时分析 ms

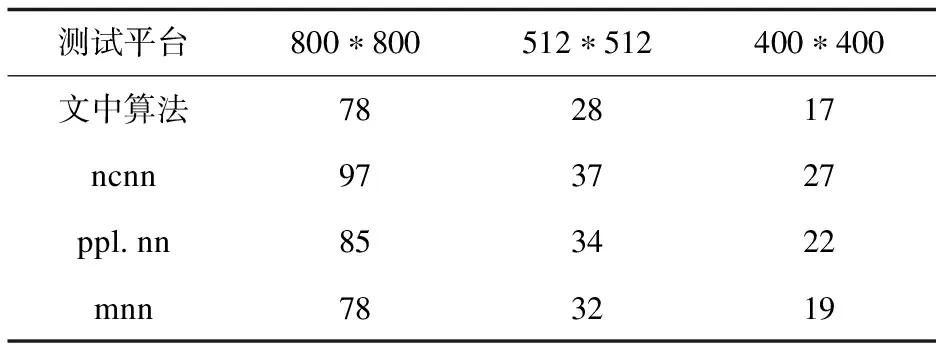
表3 逐点卷积耗时分析 ms

实验结果表明,针对普通卷积和逐通道卷积,由于ncnn框架需要提前做padding操作和单独的Add bias及relu操作,而该文提出的9宫格分块策略和访存合并优化避免了无畏的浪费,从而大大减少了访存时间,从一定程度上减少了卷积的推理耗时。在普通卷积实验中,ppl.nn之所以是几种平台中最差的,是因为需要提前将NCHW转为NHW4C之后才做卷积运算,而ncnn虽然不用提前做reorder转换,但多余的3次全量内存访问也严重影响耗时。根据2.1节分析,算法受限于访存瓶颈,因此文中算法采用直接计算(同时计算1通道输入数据和4通道输出数据),虽然无法发挥全部算力,但相比一次昂贵的reorder开销,实验表明推理耗时可以减少50%以上。

由于逐通道卷积的计算量较小,因此访存的增加反而变成最大的瓶颈,所以对于ncnn和mnn没有做访存优化(采用了单独的padding、Add bias、relu操作)。mnn虽然采用三分块(上中下)策略,对于padding策略依然使用了额外的内存布局转换,同时代码处理逻辑也是过于复杂,影响指令流水线,最后由于mnn采用NEON Intrinsics指令,相比Asm Volatile内联汇编方式要慢10%左右,而导致结果为所有平台中测试结果最差。而该文提出的9宫格算法和访存计算合并方法,对于输入数据、卷积核和输出数据,只需要从头遍历一遍即可完成卷积计算。相比于其他平台减少了至少2次以上的全量访存操作。同时又能完全发挥neon指令算力(同时计算4通道输入数据和4通道输出数据),最终算法的计算访存比达到为理论峰值的2/3。多种因素叠加使得优化高于其他平台1倍以上。且ppl.nn和mnn的代码逻辑过于复杂,过多的if语句也会导致流水线得不到充分发挥,指令预处理失败率也要高出很多。而该文从ARM A72 CPU指令性能进行分析,设计了一组能充分利用CPU流水线的指令序列,可以在同等计算量下最大化发挥处理器的算力,同时在减少分支预测和循环展开技术的加持下,最终提出的普通卷积和逐通道卷积算法耗时相比其他平台提升幅度高达75%～367%。

逐点卷积由于不需要padding操作,但ncnn依然存在多余的Add bias和relu单独操作。mnn采用了与该文类似的计算访存合并算法,因此也证实了计算访存合并方法有利地加速推理。由表3可见,与同分辨率下的逐通道卷积耗时相比也大了5～6倍。原因有几方面,首先,逐点卷积的计算访存比非常低,优化后的算法也只能达到理论的22%,相比于逐通道卷积达到理论的67%,大部分都浪费在访存上,算力得不到充分利用。其次,在相同分辨率下逐点卷积数据量要比逐通道卷积数据量多了50%,导致计算量和访存量都相应增加。最终相比其他平台提升幅度仅为9%～59%。

由于篇幅限制,仅对Retinaface典型的3种卷积算法进行针对性优化。至少在树莓派4B这一设备上,相比于国内成熟的开源框架ncnn提升了24%～367%。即使与商汤最新开源的ppl.nn框架相比,也有9%到143%不同幅度的领先。

4 结束语

针对树莓派4B设备,基于Roofline模型进行定量分析,提出了针对性的优化方法。从计算图优化,合并算子,NHW4C格式转换,到9宫格分块策略,SIMD加速方法等所有策略都是为了优化推理耗时。实验结果表明,在推理耗时上比国内大厂的开源框架ncnn和ppl.nn都有较大幅度的提升。限于篇幅原因,并未对卷积的其他类型进行分析,如dilation>1的空洞卷积。另外对于通道数比较深的卷积方法使用winograd方法[16]速度会更有优势。