一种基于阶阵列的BRIEF特征描述子

张娓娓,赵金龙,何 佳,陈绥阳,2,王 杰

(1.西安思源学院 电子信息工程学院,陕西 西安 710038;2.西安交通大学 理学院,陕西 西安 710071)

0 引 言

在图像处理领域,特征描述子对目标物的不变性研究具有重要意义。一个好的描述子应该能够抵抗目标物的尺度变化、光线变化、旋转变化、仿射变化和噪声干扰。一般而言,一个描述子的构成首先是从图像中提取一些特征点,然后根据特征点周围的区域形成描述子,最后,采用适当的距离度量方法来比对描述子的相似程度,判定描述子与目标物之间是否同一。对于视觉分类问题而言,常用的方法是通过特征向量来描述一类具有共同点的物体,然后形成可查找的视觉关键字[1-2]。假定关键点是已知的,理想的描述子应该是能够包含关键点周围区域的绝大多数重要且惟一的信息内容。

在实时性和稳定性要求严格的应用领域,描述子必须能够提供快速的计算和比对结果,这就需要设计一个稳定而高效的描述子,人们为此开展了大量的实验和研究。其中,为了满足描述子的抗尺度不变性,Lowe提出了基于直方图计算梯度主方向的方法[3-4],这一方法是在一系列尺度下,对经过高斯滤波的特征点周围区域的灰度值进行采样,计算出图像主方向。该方法被广泛用于描述关键点的方向性。类似的计算主方向的方法还有GLOH[5]和HOG[6]。虽然这些方法并不能很直观地反映图像空间频率关系,但它们拥有很准确的方向判断性。此外,SURF描述子主要利用特征点周围像素点对HAAR滤波的响应来提高运算速度[7-8],其性能不亚于SIFT描述子。即使如此,SIFT和SURF描述子的计算代价依然很高,不能很好地应用于实时图像处理。为此,Ke和Skthankar[9]提出在计算SIFT描述子主元时,采用PCA方法对特征点周围41×41的像斑区域进行计算,从而将原有的2×39×39维的向量降低成20维向量,形成更为精准的PCA-SIFT描述子。PCA-SIFT描述子保留了SIFT描述子的尺度不变性,同时降低了特征向量维数,但在计算描述子过程中会增加一定的计算量和损失少量的差异性。Bin基于阶序组合池提出了两种抗旋转不变的描述子[10]:一种是MROGH(Multi-support Region Order-based Gradient Histogram),主要是对特征汇聚策略进行了改进;另一种是MRRID(Multi-support Region Rotation and Intensity Monotonic Invariant Descriptor)。Miksik和Mikolajczyk通过实验验证了基于阶排列的描述子的计算复杂度要低于SIFT和SURF[5,11]。LIOP(Local Intensity Order Pattern)方法进一步证实这一观点[12],LIOP是一种用来刻画图像局部亮度顺序信息的特征描述方法。该特征描述方法利用图像(块)整体的亮度顺序信息将图像块分割为若干个局部子区域,以此来加快LIOP的计算速度。整个图像块的整体和局部亮度顺序信息被提取出来,构成LIOP特征。这种特征不仅对光照变换不敏感,对视角变化、图像模糊、图像有损压缩等也同样不敏感。

除了实时应用需求,在大规模数据运算和移动设备上,计算量也是一个至关重要的约束条件。计算量小的描述子主要有Calonder提出的二值特征描述子BRIEF[13-14],以及基于BRIEF的抗尺度变化和旋转变化的改进特征描述子BRISK[15]。此外,ORB也是一种具有抗旋转不变性、计算高效的描述子[16],它采用了基于FAST算子的特征点检测方法。Ziegler也提出了一种线性时间复杂度的描述子[17],该描述子通过对两张图片的RGB分块值进行排序,结合排序后序列的距离,实现对图片的特征描述[18]。

该文提出一种基于BRIEF的改进的阶排列描述子OPoBRIEF (Order Permutation of BRIEF)。OPoBRIEF采样多组对比对进行分析,并对采样点进行排列,从而形成局部特征描述。该方法比BRIEF描述子包含更多的局部信息,而且计算简单,易于实现。首先,介绍BRIEF相关概念;然后,将BRIEF描述子扩展到N维,为后续的阶排列提供基础,并分析采样过程中使用box filter的滤波效果,以及序列的距离度量计算方式;最后对OPoBRIEF的主要性能进行实验分析。

1 相关描述子简介

BRIEF特征描述子由Calonder等在ECCV’2010上提出[1],基本思想是对特征点附近的分块区域随机采样,将采样的像素对灰度化后进行比较,比较结果形成一个二进制串,将这个二进制串作为该特征点的特征描述子。BRIEF特征描述子的主要优点是计算简单,匹配效率高,能满足实时视频或者移动计算环境的要求。

1.1 BRIEF描述子

定义一个经过高斯平滑后的图像块p,图像块的大小为s×s,随机在块中采样一对像素点进行比较,比较结果由下式决定。

(1)

式中,I(p,x)表示第p个图像块中的像素点x的灰度值,I(p,y)表示第p个图像块中的像素点y的灰度值。在块p中随机采样n对对比对,形成一个n维的二进制描述串,也就是BRIEF描述子,如下:

(2)

在选取采样点时,采样点的空间分布应服从高斯分布,保证采样更为全局化。描述子向量之间的距离可以采用汉明距离,通过异或操作实现快速计算。通常,nd代表了形成的二值序列的维度,可以取值为128、256、512。BRIEF描述子的一个采样实例如图1所示。

图1 BRIEF 相关的空间采样

1.2 ORB描述子

BRIEF描述子本身仅考虑了单个像素,不具备方向,也就不具有旋转不变性。ORB描述子尝试给BRIEF添加一个方向,特征点的主方向是通过矩(moment)和图像矩心计算而来,然后,通过贪心算法寻找二值准则特征集中相关性最低的对比对集合,作为ORB描述子。图2显示了在大小为31×31的图像块上,采用5×5大小的子窗口进行处理后获得的ORB描述子。

图2 ORB相关的空间采样

1.3 BRISK描述子

BRISK描述子采用领域采样模式,即在以特征点为中心的每个离散化同心圆上,取均匀分布的N个点,如图3所示。BRISK描述子具有旋转不变性和尺度不变性的特点。文献[10]中BRISK采用了不同尺度高斯平滑去噪技术,并使用FAST算子值作为度量局部的最大性指标,在多尺度空间上寻找最值,使其具有尺度不变性;为了适应旋转不变性,在建立描述子的过程中,利用长距离点对的梯度累加从而估计特征点角点的主方向。

图3 BRISK相关的空间采样

2 OPoBRIEF描述子

Ziegler通过随机提取图像局部的像素对,比对灰度值形成二值序列,然后计算汉明距离(hamming distance)进行相似匹配[17]。考虑到灰度对比对的不稳定性,首先增加采样点数量,然后引入阶排列的概念,加强对二值对比对的条件约束,最后形成更为稳定的阶排列BRIEF描述子。

2.1 N维BRIEF描述子

Calonder提出的BRIEF描述子只是利用局部图像邻域内两个随机点的灰度关系来建立局部图像特征描述子,得到的是二值特征描述子。这种方法结构简单,计算速度快。但是,由于只选取了两个采样点,所构成的对比对的关系比较简单,使得描述子不够稳定。通过对局部图像块进行多次采样形成一个采样组,组内采样点数为n(n>2),进而引入采样点的阶排列的概念,提出OPoBRIEF描述子。

由于有多个采样点需要进行比对,首先对式(1)进行扩展。给定从基准图和测试图中提取特征关键点的集合为χ,χ⊆Rs,且采样图像的分块区域都经过平滑处理,降低了图像灰度值的一些噪声影响。获得描述子后,可以通过计算不同集合下采样组的相似关系来进行特征匹配。每组采样点中组内采样点的二值测试序列可以描述为:

(3)

实际上,Calonder所介绍的二值序列BRIEF特征描述子是ns=2时的情况,即式(1)替换表示为:

(4)

用来形成二值序列串的描述子式也可以扩展到nd维,表示为:

(5)

在OPoBRIEF中,阶排列是用在有多个采样点的情况。例如图4情况,在平滑过的子块上随机抽取4个采样点:I(x(j,1))=60,I(x(j,2))=160,I(x(j,3))=15,I(x(j,4))=200,该组采样点的阶排列字串为4 213。

通过计算得到的阶排列来替换BRIEF描述子中的二值测试序列,则OPoBRIEF描述子对每个特征点的维度变化为nd×ns。显然,ns值过大会造成阶排列字串过于复杂,通常ns取值为3和4较为合适,两者的阶排列模式只有6和24,计算开销较小。

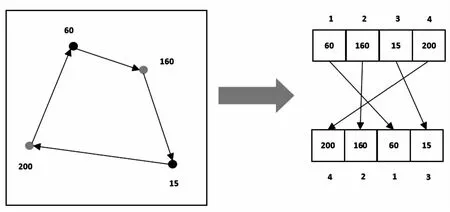
图4 构造阶排列的过程

2.2 平滑核的选择

高斯噪声可能损坏阶排列的稳定性,主要原因是噪声会引起像素值局部极大值或者极小值突变,从而改变灰度值在特征向量里的排列顺序。为此,采用不同大小的高斯核滤波和不同窗口的Boxing滤波,研究测试OPoBRIEF的稳定性。

通常来说,Boxing滤波的窗口尺寸越大,阶排列得到的结果就越稳定。但是,这会导致同样的阶排列生成不同的排列串。为避免这一问题,该文尝试通过在一些公共图像测试集上进行实验,寻找一个窗口大小合适的Boxing滤波。图5给出在测试图像集合Benchmark上,采用不同窗口大小的Boxing滤波算法,对不同种类的图像集合进行平滑后,描述子的正确匹配率实验结果。其中,分块大小p=48、维度nd=256,每一组实验包含了8个不同大小窗口的Boxing滤波测试的结果。由图可见,当k值在13附近时,Boxing滤波能够达到较高正确匹配率。

图5 不同窗口大小Boxing滤波后描述子的正确匹配率

Calonder建议采用48×48的分块、7×7的窗口和δ=2高斯核进行滤波处理,能够获得稳定的效果[11]。实验结果表明,采用boxing滤波比高斯滤波的效果更好,稳定性高于高斯滤波,实验结果优于文献[13]。另一方面,考虑到构造一个boxing滤波只需要四个点和三次加法运算,算法更为简单有效,更适用于进行区域分块平滑滤波。

2.3 阶排列距离度量

Ziegler介绍了三种不同的高效的距离计算方法[17]:Hamming距离、Cayley距离和Kendall's tau距离。其中Kendall's tau距离已经被证明在计算阶排列的距离上要比其他两种计算方法好,虽然它的计算复杂度为O(m2),高于汉明距离和Cayley距离的计算复杂度O(m)。

Kd(π1,π2)=|{(i,j)|(π1(i)<π1(j)∧π2(i)>π2(j))∨(π1(i)>π1(j)∧π2(i)<π2(j)),1≤i,j≤ns}|

(6)

3 实验与结果

在公共图像数据集上进行了不同采样大小的测试。首先计算了ns=3和ns=4情况下提取的OPoBRIEF描述子,并与BRIEF进行对比;而后又对OPoBRIEF的旋转不变性进行了实验和分析。实验硬件环境:Intel(R) 双核CPU-E7500,主频2.9 GHz,6.0 GB内存,软件环境:Linux系统,基于OpenCV类库采用C语言编程。

3.1 描述子稳定性实验

实验选取五个不同的图片数据集wall、ubc、leuve、trees和bikes进行测试,每组图片6个,如图6所示。这五个不同的数据集可用来测试在不同情况下图像变换对描述子稳定性的影响。其中,wall主要针对的是相机的镜头视点的改变;ubc主要针对的是图像压缩率的变化;leuve主要针对的是图像的光照变化;trees和bikes主要针对的是图像的模糊变化。

图6 图像测试集示例

Surf算法是OpenCV中一个快速和高效的特征点检测算法,因此,该文主要采用Surf进行关键点提取。表1是每组图片比对结果,在最高匹配率前面加上了星号做标记。表1记录了在nd=256的情况下,3采样点OPoB-3,4采样点OPoB-4和BRIEF(B-256)三种方法的实验结果。

表1 不同数据集的正确匹配率

通过分析表1的实验结果可以发现,除了第一组实验,OPoBRIEF比BRIEF的整体匹配效果好,其中,OPoB-4比OPoB-3的整体匹配效果更好,OPoB-4的正确匹配率高于BRIEF。实验结果同时说明选择的采样点数量越多,描述子包含的信息量越多,匹配的正确性也就越高。在测试描述子对旋转不变性的实验中,描述子OPoBRIEF的匹配效果并不比BRIEF描述子好很多。在trees和bikes测试集上的实验结果表明,OPoB-4的匹配效果明显优于OPOB-3和BRIEF。尤其是在trees的数据集上,描述子OPOB-4要比描述子BRIEF平均多出21对以上的正确匹配对,这说明描述子OPoBRIEF对图像的模糊有较强的抵抗性。而在用来测试光照变化对描述子影响的数据集leuve上,OPOB-4的效果也明显优于OPOB-3和BRIEF。最后在不同压缩率比图像的测试中,BRIEF的性能大多数情况会好过OPoBRIEF,但两者的差距并不是十分巨大。

3.2 OPoBRIEF的旋转不变性实验

为了检验OPoBRIEF的旋转不变性,设计了一组实验。实验所用的数据集是new york图片序列,该图片序列包含了35张图片,覆盖了从0到170和170到350度旋转的图片。特征点的提取算法使用的是最新版OpenCV中的SIFT和ORB算法,其中使用SIFT特征点提取法获得26 235对匹配对,使用ORB算法获得26 430对匹配对。如果考虑每10度作为一个错误区间,则有26 200对匹配对被衡量。实验结果如表2所示,提供了错误区间为10到50的实验结果。从实验结果可以发现,SIFT算法的主方向的准确率为69.03%,要远高于ORB算法的主方向的准确率57.95%,但在其他旋转度SIFT算法不及ORB。通常算法中都会选用10度到12度作为偏移区间,因此,SIFT主方向计算方法更能满足该文的主方向计算需求。SIFT与OPoBRIEF的对比结果如图7所示,表明OPoBRIEF的旋转不变性不亚于SIFT特征描述子的效果。

表2 不同旋转度的匹配率

图7 OPoBRIEF与SIFT特征描述子旋转不变性比较

3.3 实验结果

在上述稳定性实验中,选择采样点数量越多,描述子包含的信息量越多,匹配的正确性也相应越高,说明OPoBRIEF比BRIEF的整体匹配效果好。在测试描述子对旋转不变性的实验中,描述子OPoBRIEF的匹配效果也好于BRIEF描述子,对于SIFT特征描述子来说,OPoBRIEF的旋转不变性更加稳定。

4 结束语

对二值描述子BRIEF进行了改进,引入了更多的对比对来加强特征描述子的信息包含量,并引入了灰度值的序排序,提出了一种改进的描述子OPoBRIEF。与BRIEF描述子相比,OPoBRIEF需要增加的计算开销很少,适合移动与实时计算环境;选择三采样点(OPoB-3)和四采样点(OPoB-4)进行了实验,结果表明提出的描述子稳定性更好;进一步的实验还证明,采用Kendall's tau距离进行描述子匹配时,该方法的匹配效果更好。