激光微织构分布与形状对轮轨线接触下润滑性能的影响
周渝钧,区俊杰,郑润婷,欧洋婷,刘吉华,何成刚,林群煦
(1.五邑大学 轨道交通学院,广东 江门 529020;2.广东工业大学 机电工程学院,广东 广州 510006)
地铁作为绿色、环保、高效的交通工具,是未来城市轨道交通的发展趋势. 由于城市地理环境复杂,使得在地铁线路的设计中不得不采用数量众多的小半径曲线,这造成轮轨材料产生了不同程度的轮缘磨耗和钢轨侧磨[1]. 结合长期地铁现场运营积累的经验,以及各个城市和不同地铁路段的不同情况,我国学者对改善轮缘磨耗给出了相应的建议:如制定车轮定期掉头运行机制[2]、控制小半径曲线列车速度[3],对于已经发生轮缘异常磨耗的车轮通过镟修的方式恢复车轮至设计外形[4-5],在运行过程中通过使用轮缘/钢轨轨距角润滑系统来改善轮缘和轨距角的接触状态[6-7]. 国外轮轨关系研究学者针对轮缘润滑开展了大量的探索与研究. 美国联合铁路公司的Thelen等[8]早在1996年就基于全尺寸试验和现场试验发现轮轨表面粗糙度、轮轨型面尺寸等参数对轮缘润滑效率的影响规律. 巴西圣埃斯皮里图联邦大学的Almeida等[9]利用销盘试验机研究了不同车轮材料的轮缘与钢轨轨距角的滑动摩擦行为. 国内金泰木等[10]探究了轮缘润滑对重载列车曲线通过性能的影响,发现当机车通过小半径曲线且处于轮缘润滑状态时,轮对的导向性能将减弱. 西南交通大学温邦等[11]探究地铁车辆轮缘润滑对车轮磨耗的影响,建议在正线中、在润滑状态下给列车整车安装轮缘润滑器.
对于轮缘磨耗,英国谢菲尔德大学的Fukagai和Lewis教授[12]提出在车轮和钢轨表面引入表面纹理,以此降低车辆爬坡脱轨风险. 研究表明,在某些接触表面进行相应的凹坑设计可以起到储油与减磨的作用[13-14]. 激光表面微织构能够储存润滑介质,使得接触界面形成动压效应,进而改善摩擦副间的接触状态,已经被广泛运用于机械行业摩擦表面,如汽车内燃机中的密封环、气缸、止推轴承、机床导轨以及频繁启停的部件[15-16]. 本文拟将激光微织构应用于轮缘和钢轨轨距角的接触界面,利用大滑差线接触状态模拟地铁车辆通过小曲线半径类曲线路段,探讨不同激光微织构参数(形貌、分布率)及试验过程喷涂油量对轮缘/轨距角润滑效率的影响规律,旨在提高地铁车辆轮缘/轨旁润滑系统的润滑效率,缓解地铁车辆通过小曲线半径路段轮轨材料的损伤.
1 试验部分
1.1 激光表面微造型试验
用光纤激光打标机对钢轨试样表面进行表面微造型打标. 光纤打标机的主要参数包括:激光功率、激光频率、旋转轴速度以及打标次数,通过调节上述参数可以改变微造型的形貌. 对比分析不同激光功率与激光频率下凹坑三维形貌图发现:35 kHz、18 W 时所制备的凹坑深度、直径及外观形貌较为规律,且分布均匀.
由于地铁车辆通过小半径曲线路段时轮轨之间的接触应力很大(最高能达到1 600 MPa),若采用微米级的小凹坑很容易在试验过程中被磨除,所以本研究拟在规则的宏观形貌下填充微米级的凹坑,从而保证微造型凹坑不容易磨除. 本文设计了矩形、圆形与菱形的激光微造型,并以50 μm 的微小圆形进行阵排列,具体如图1-a所示,进而得到钢轨试样表面的激光微造型,如图1-b所示. 通过NaoMap-D型三维形貌仪对微造型形貌进行观察,发现制备的微造型中凹坑阵列形式明显、凹坑整体形貌规则有序,如图1-c所示.
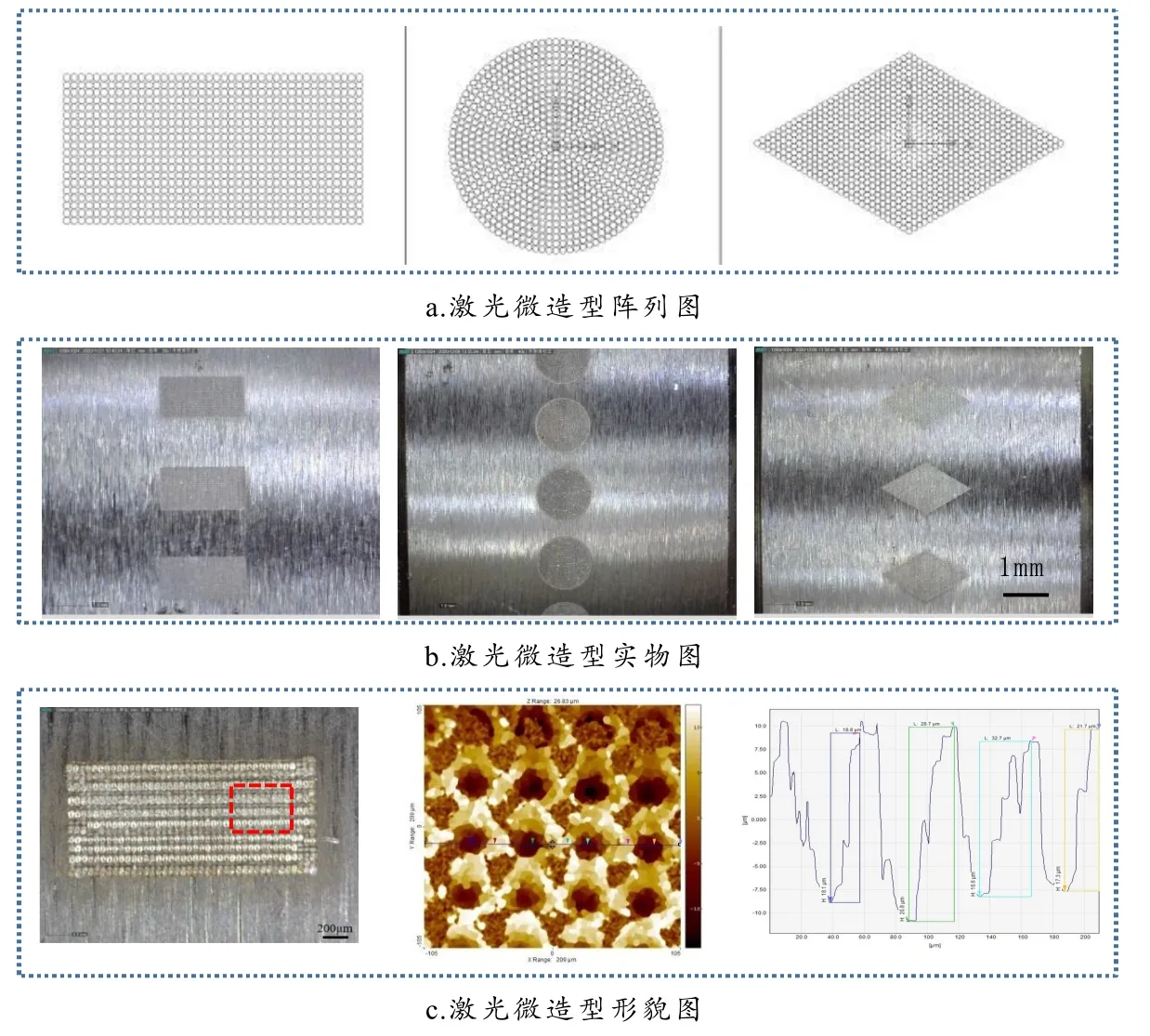
图1 不同激光微造型的分布、形状及局部形貌图
在钢轨试样表面制备矩形、圆形及菱形形貌,在各个宏观微造型内以小凹坑进行阵列填充,且保持各个宏观微造型面积均为 2 mm2,即矩形尺寸为1 mm ×2 mm,圆形直径为1.8 mm,菱形边长约为1.52 mm. 根据宏观微造型形貌面积及钢轨试样表面面积,对微造型分布率进行推导:
式中,n为凹坑个数;r为内部填充凹坑的半径,约20 μm;S为单个微造型面积;m为单个微造型个数;l为钢轨试样表面宽度;R为钢轨试样半径,20 mm.
1.2 轮缘润滑试验
本研究涉及微造型分布率、喷涂油量及微造型形貌三组试验水平变量,为优化试验引入正交试验设计,其具体因素水平如表1所示,得到的实验设计如表2所示.

表1 因素水平表
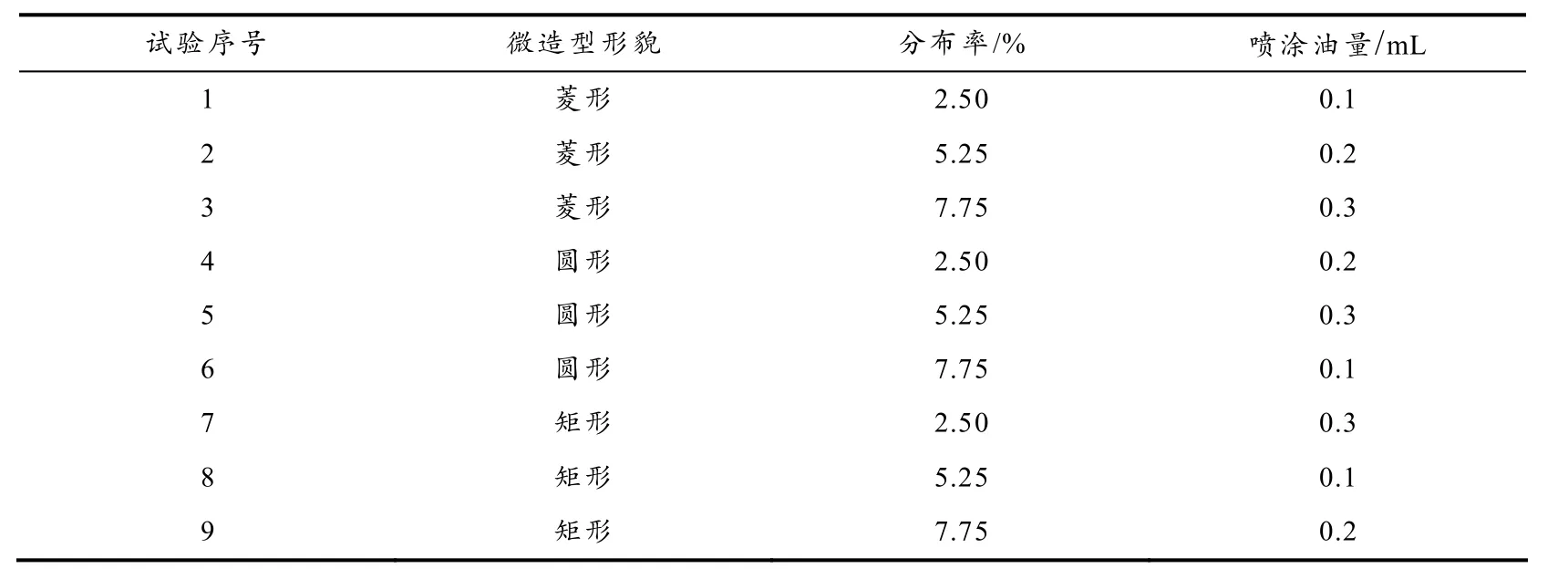
表2 三种变量下的正交试验设计
为探讨多因素水平对轮缘润滑的影响,本研究拟在MMS-2A磨损试验机上开展轮缘润滑饥饿试验[17]. 轮轨试样尺寸如图2-b所示,下试样为车轮试样,上下试样均为圆环形状,采用线接触形式.两试样内、外径分别为16 mm 和40 mm,轮轨试样接触宽度为5 mm. 根据赫兹接触模拟准则,实验室模拟轮轨间最大接触应力为400 MPa,轮轨间滑差率为10%,车轮转速为200 r/min. 经计算上试样转速为180 r/min,轮轨间垂向试验力为230 N. 本文拟通过轮缘润滑饥饿试验考察三种变量对轮轨润滑效率的影响,通过分析轮轨间摩擦系数变化规律得出润滑性能最优的方案. 考虑到试验过程中较大油量(如0.3 mL)的润滑持续时间远大于较小油量(如0.1 mL)的,为保证后期正交试验分析的准确性,本文以润滑状态时间与总时间的比值作为评判标准,即通过时间比来判断润滑性能的优劣.
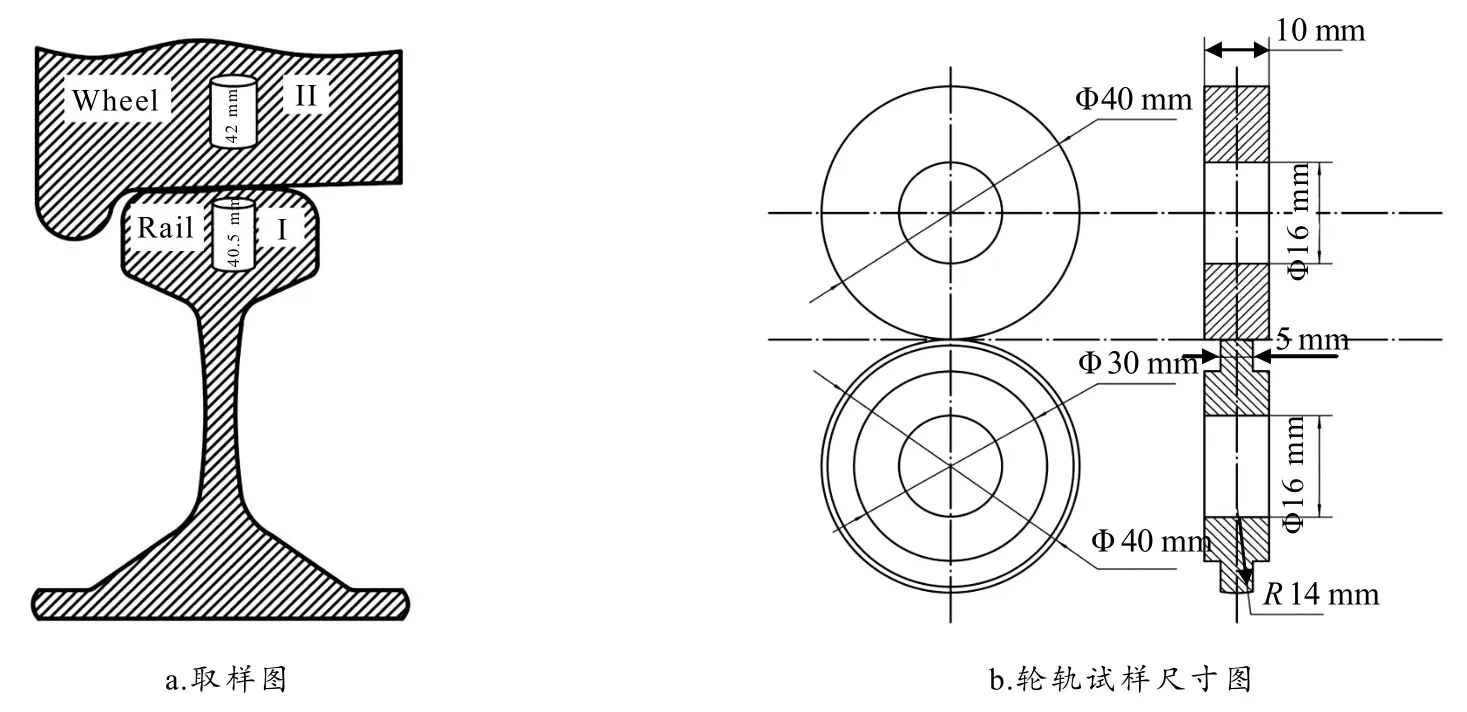
图2 取样图及轮轨试样尺寸
2 实验结果分析
2.1 轮缘润滑试验结果
按表2设计进行轮缘润滑饥饿试验,依次将钢轨试样与车轮试样安装到试验台,并设置转速、试验力等具体参数. 试验初期,轮轨之间进行干摩擦,摩擦系数随时间不断上升,当摩擦系数达到0.35左右并稳定后利用注射器从法向方向喷涂预先设计的油量,摩擦系数骤降,达到0.23左右维持稳定,轮缘润滑实物图如图3所示. 随着时间的推移,轮轨间的摩擦系数逐渐升高,最终再次维持在0.35左右,随后重复喷涂润滑油.

图3 润滑状态下的运行工况图
轮缘润滑饥饿试验后对轮轨摩擦系数进行归类分析,具体结果如图4所示:
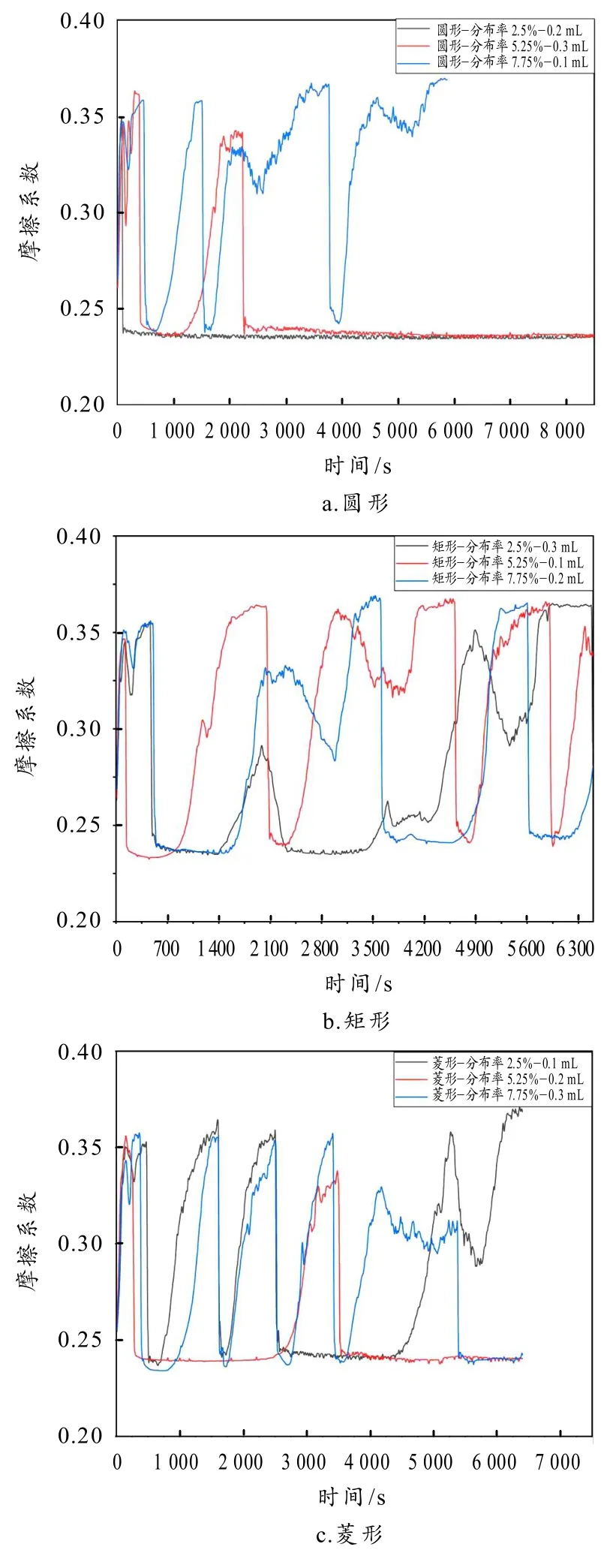
图4 三组形貌对应的时间-摩擦系数图
1)图4-a圆形形貌对应的三组试验,其润滑效率规律随机性较大,该形貌的润滑持续时间与未进行激光微造型处理的钢轨试样没有太大的区别. 在试验过程中,随着润滑脂的不断堆积,在轮轨润滑界面中出现了“二次润滑现象”[18],这导致了摩擦系数的波动.
2)矩形形貌的部分曲线可以总结出一定的润滑特性规律,但仍然受“二次润滑现象”的干扰,如图4-b所示. 值得注意的是在试验初期,由于还没有产生大量的润滑脂堆积,所以在第一个润滑周期内,摩擦系数极少出现再次润滑现象,但随着时间的推移,“二次润滑现象”更加明显. 在黑线(矩形、分布率2.50%和用油量0.3 mL)中,由于0.3 mL 自身的一次性喷涂量较大,在第一次喷涂后就造成了钢轨试样两侧大量的润滑油堆积,进而在第一个润滑周期内出现了3次“二次润滑现象”,其余两组试验均是在试验中后期出现二次润滑的现象. “二次润滑现象”在试验中有效提高了润滑时间与总时间的比值,从理论上看能够起到更好的润滑维持性能,但在未来的现场应用中,这种现象存在明显弊端,如在现场应用过程中很难随时把控其自身润滑规律,需要进行大量的数据调研和统计,才能大致推算出其润滑规律来指导现场应用.
3)图4-c为菱形形貌的时间-摩擦系数图,其在磨损试验初期均未出现“二次润滑现象”,其中黑线(菱形、分布率2.50%和用油量0.1 mL)与蓝线(菱形、分布率7.75%和用油量0.3 mL)的前4个润滑周期规律相似,且润滑持续时间相近,红线(菱形、分布率5.25%和用油量0.2 mL)工况下润滑持续时间较长,且在该状态下并未出现“二次润滑现象”.
4)图4-a中的黑线(圆形、分布率2.50%和用油量0.2 mL)与图4-c的红线(菱形、分布率5.25%和用油量为0.2 mL)在润滑状态下的持续时间比较长,显然与传统润滑的观点“所喷涂的润滑脂越多,其润滑时间就越久”[19-20]不相符,也证明了微造型对润滑有很大影响.
2.2 正交试验分析
本研究中数据组为3因素3水平的正交试验 L9(34)以及每一次实验所测得的润滑时分比H(润滑维持时间∶总时间),结果列于表3,加油时间点的选取、加油位置、加油速度、轮轨安装位置等条件一致. 从表3可以看出润滑时分比的范围为4.9%~78.59%,其中水平组合A2B1C2(菱形、分布率5.25%和喷涂油量0.2 mL)的润滑时分比H最高(78.59%).
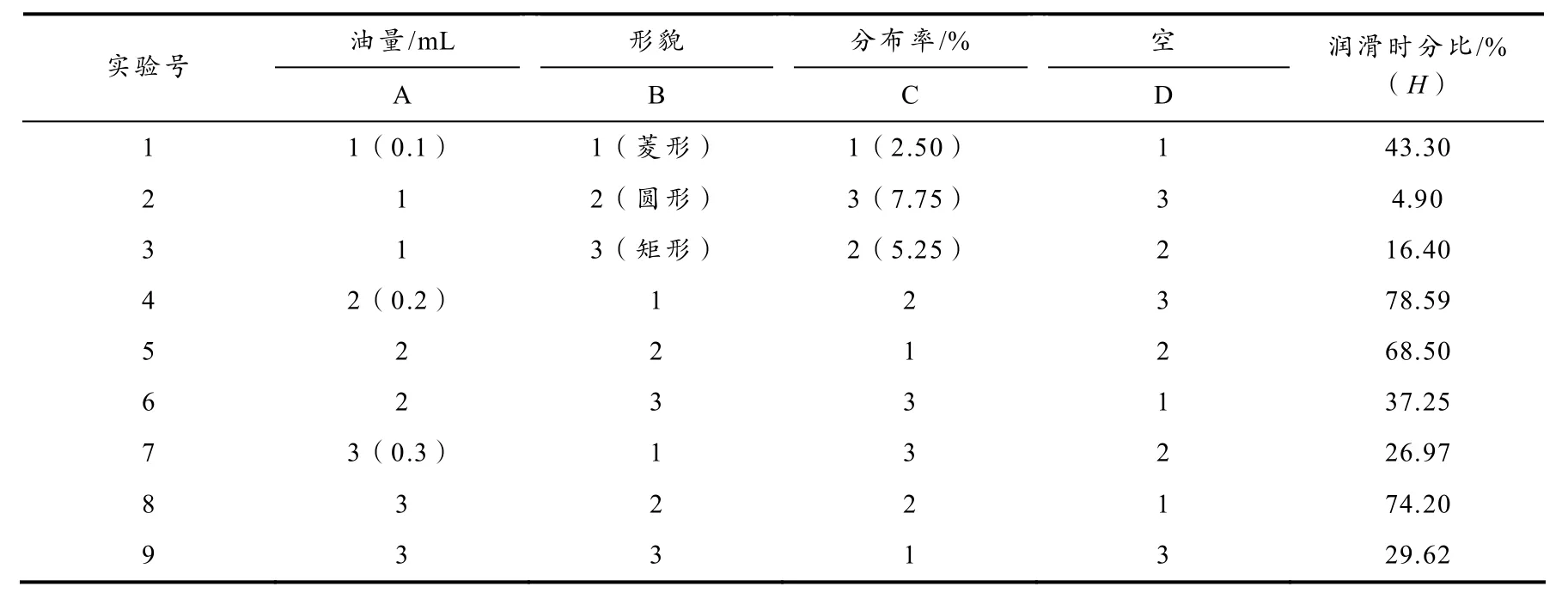
表3 正交试验分配表
三组水平变量试验所涉及的试验共有27组,而现根据正交试验设计只完成了其中最具代表性的9组试验. 由于这9组实验中最好的结果不一定是整个27组试验中最好的,故需要进一步利用正交试验进行分析. 本文采用正交试验的直观分析法来分析轮轨润滑效果的最优水平组合. 一般定义Tij为表3第j列中与水平i相对应的各次实验结果之和(i=1,2,3;j=1,2,3);记T为9次实验结果的总和,Rj为第j列的3个Tij的极差(极差越大对试验结果的影响越大). 按该方法,对因素A在每一水平下所做试验的H值进行加和、取极差,结果如表4所示.

表4 T 值计算结果
表4中因素A的Rj计算值最大,其9次试验结果的总和为379.73,四因素极差大小的顺序为A,B,C,D. 由此可以看出:要使润滑时分比H最优,需要优先控制好因素A(喷涂油量)和C(分布率),其次是要考虑因素B(微造型形貌)和D(空列). 为方便计算. 引入空列D作为数据组,在表4一列中选取最大的T21(即取水平A2),同理可选出最好的因素水平搭配是A2B1C2D1,即轮缘涂油量选用0.2 mL、激光微织构形貌为菱形形貌,分布率为5.25%时,这一组的时分比H最优,轮轨润滑效果最好. 直观分析法虽然直观、简单和便捷,但未考虑误差对试验数据的影响,极大降低了试验数据分析的准确性,可采用方差分析来确认数据的准确性. 方差分析又称“变异数分析”,它通过公式计算推导出各数据之间的差异是否显著,并以此确定多个因素的主效应和数据之间相互的交互作用[21-23]. 以上3种因素对H影响的显著性以及整个正交设计试验置信度的方差分析结果如表5所示.
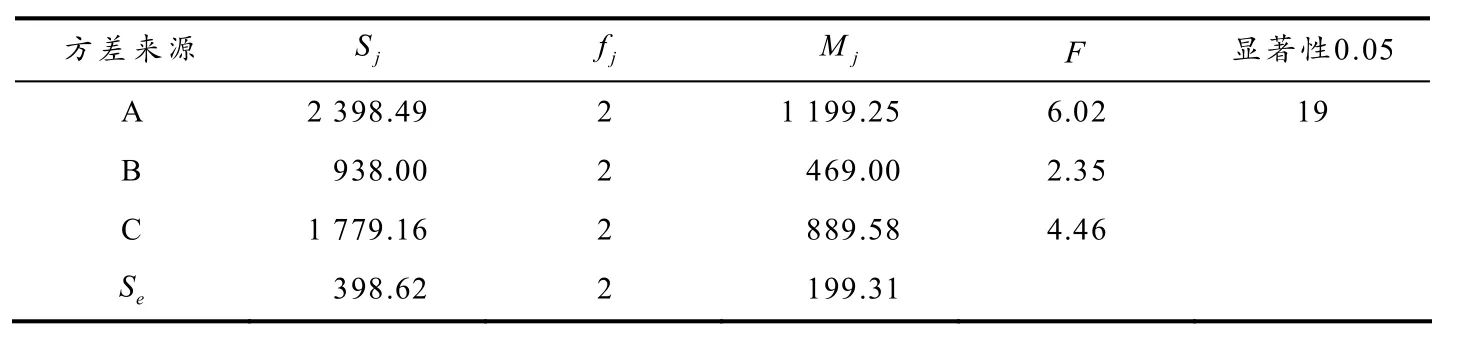
表5 方差分析表
表5结果表明:三个因素对时间比H的影响都不显著,究其原因是本例试验误差大且误差自由度小,使检验的灵敏度低,从而掩盖了考察因素的显著性. 由于各因素对摩擦系数影响都不显著,故不必再进行各因素水平间的多重比较. 此时,可从表4中选择平均数大的水平A2B1C2(菱形、分布率5.25%和用油量0.2 mL)组合为最优水平.
3 结论
为解决轮缘/轨矩角润滑容易造成轨道污染和润滑脂大量浪费的问题,创新性地在钢轨轨矩角表面制备具备储油功能的激光微织构,利用正交试验设计方法对试验和结果进行分析,得出以下结论:
1)在时间-摩擦系数曲线中,干态下摩擦系数始终维持在 0.35 左右,润滑状态下维持在 0.23左右,改变微造型形貌、分布率及润滑脂的喷涂量时,摩擦系数的大小均未出现明显的变化. 所以,在润滑状态下摩擦系数的大小只与润滑脂的自身性能有关,与激光微造型的形貌等因素无关. 对比菱形、矩形和圆形三组形貌的试验数据,可以清晰看到部分用油量大的试验组,其润滑性能并非全部优于用油量少的试验组,这打破了传统润滑“喷涂润滑介质越多,润滑状态保持时间越久,润滑性能越优异”的观点. 进一步试验证明,激光微造型形貌的种类与分布率在轮缘润滑过程中起着至关重要的作用,故将激光微造型技术引入到轮轨润滑界面十分必要.
2)通过正交试验设计出9组试验,并根据数理统计分析得出最优的方案为 A2B1C2D1(菱形形貌、分布率5.25%和用油量0.2 mL,D为空列). 三种水平变量(微造型形貌、分布率和喷涂油量)对轮缘润滑性能的影响中,润滑脂的喷涂油量与激光微造型的分布率起着主要影响因素,微造型形貌种类为次要因素. 这一结论为日后进一步开展相应课题研究提供了方向.

