条形基础加载下软弱夹层边坡应变特征及其与稳定性的关系研究
田野
(中铁十八局第五工程有限公司,天津 300459)
随着我国基础设施的快速发展,临近边坡区域常常会修建各种构筑物或建筑物,尤其是西部盆地和山谷地区,如重庆等[1-3]. 坡顶构筑物的修建将对边坡形成附加荷载,改变边坡内部应力分布及其稳定性状态,尤其是边坡在极端荷载作用下易发生失稳破坏,从而威胁公共安全[4-5]. 因此,对荷载作用下边坡的应变及位移等特征进行实时监测,进而对边坡稳定性进行判断已成为有关部门的重要任务.
目前,国内外学者在荷载作用下边坡稳定性方面进行了大量探索. 如Hanna[6]、Li[7]等采用全球定位系统(GPS)等方法对边坡地表位移进行监测,但该方法受降雨、植被等不确定因素影响较大.另一方面,Zhu[3]、Wang[8]、孙巍锋[9]等采用分布式光纤传感技术等对边坡应变特征进行实时监测,从而更精确对边坡稳定性进行评价. 对位移特征而言,边坡应力应变的累积变化更能体现边坡的劣化过程,因此通过对边坡应变分布规律进行分析,有助于评价边坡的稳定性状态与潜在滑面位置等.基于此,Zhu[3]、唐胜传[10]、黄诗渊[11]等学者基于数值模拟方法,分析了边坡稳定性系数与最大水平应变的关系,结果表明边坡稳定性系数与不同位置的最大应变存在较好的拟合关系,如线性关系、对数函数关系等. 实际工程中边坡多含有多层岩土体,且常常含强度较低的软弱夹层,对边坡稳定性造成一定影响;此外,现有研究已表明荷载的大小、宽度、位置等对边坡破坏模式、应变特征等具有重要影响[12-13],然而现有关于边坡稳定性与应变关系的研究主要针对均质土体边坡,且很少考虑荷载形式的影响.
因此,本文将建立不同宽度和位置荷载作用下软弱夹层边坡稳定性分析模型,采用有限元法分析加载过程中软弱夹层边坡不同高程处水平应变和位移的变化规律,探讨不同形式荷载作用下边坡稳定性与应变的拟合关系,为现场应变传感器等布置提供理论指导.
1 条形基础荷载作用下软弱夹层边坡稳定性计算模型
本文边坡模型参照S228 狼山至镇边城公路狼山至东花园段改建工程项目土质边坡[14],边坡土层为水平三层分布,其性能参数见表1,其中土体2 的物理力学性能较差,为软弱夹层. 图1 为边坡简化模型示意图,模型高15 m,长50 m,坡度为 1.5 :1,坡顶处施加条形基础载荷,三土体层从上至下的厚度分别为6 m、4 m 和5 m;计算模型具体尺寸参数见图1. 由于本文主要目的是研究不同形式条形基础荷载作用下软弱夹层边坡的应变特征与稳定性问题,因此根据有关学者研究[3,10-11],未考虑地下水对边坡的影响. 土体破坏准则采用摩尔-库伦强度理论. 为获得边坡在破坏过程中的变形演化情况,在边坡不同高程处从低到高按间隔2 m 依次设置H1、H2、H3、H4、H5和H6等6 条水平应变测线,以便监测边坡不同高程处的应变分布规律;在坡肩位置由外向里按间隔6 m 设置两条竖向位移监测线V1和V2,以便获得不同高程边坡处的水平位移.

图1 条形基础荷载加载下软弱夹层边坡计算模型及网格划分图
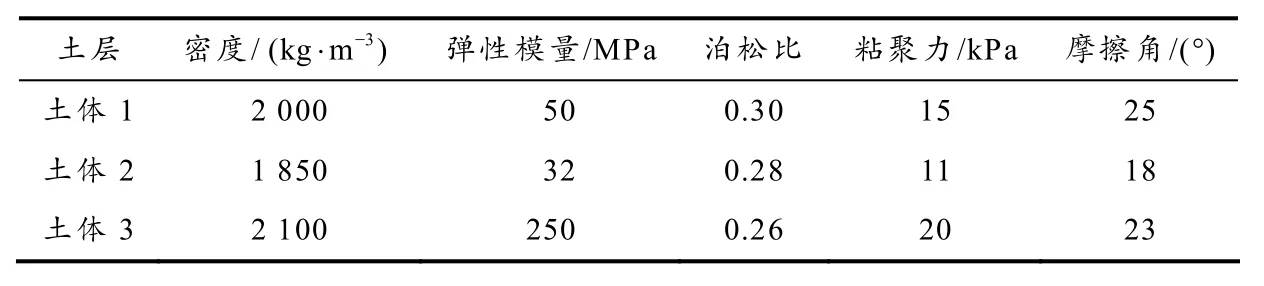
表1 岩土体参数表
为分析条形基础载荷宽度、载荷位置及其加载大小等对含软弱夹层边坡变形特征的影响及其控制,本文分别建立不同条形基础载荷宽度和载荷位置的边坡计算模型,具体为:1)固定条形基础载荷位置,即距坡顶距离1L为4 m,载荷宽度2L分别设置为4 m、6 m、8 m 和10 m;2)固定条形基础载荷宽度2L为4 m,距坡顶距离1L分别设置0 m、4 m、8 m 和12 m. 在边坡模型计算过程中,对条形基础载荷q进行线性逐级加载,每级加载10 kPa,直至边坡模型计算不收敛,表明该边坡已达到破坏状态[15-16]. 此外,利用Bishop 法计算不同大小载荷作用下路堤边坡的稳定性系数. 如图1 所示,模型网格大小设置为0.25 m;模型底部约束其水平位移和竖向位移,左右两侧约束其水平位移.
2 条形基础荷载作用下软弱夹层边坡的变形过程分析
2.1 加载过程中边坡变形分布规律
2.1.1 加载过程中边坡水平应变分布
对条形基础荷载距坡肩L1=4 m、加载宽度L2=4 m的软弱夹层边坡进行逐级加载计算,得到了不同大小荷载作用下边坡的应力应变特征. 图2 为条形荷载加载过程中软弱夹层边坡水平应变云图的演化过程. 在加载初期(如荷载为20 kPa),基础荷载与边坡顶部接触区域为压应变,而在荷载下部较深坡体内形成了较大范围的水平拉应变,且主要集中在软弱夹层中. 随着荷载加载的增加,荷载对边坡的作用区域压应变值不断增大,且作用范围扩大;坡体内部的水平拉应变值进一步增大,加载70 kPa 和120 kPa 时比20 kPa 分别增大了10.3 倍和21.5 倍,但其集中区域范围缩小,且向边坡上部移动. 随着荷载进一步增加,如荷载为120 kPa 时,基础荷载的左、右边界出现拉应变(尤其是左边界),且与坡体中上部的拉应变区域贯通. 当荷载进一步增大到边坡失稳时(170 kPa),坡脚处的水平拉应变增大,且与坡体中上部的拉应变区域连通,形成连续的拉应变滑带(如图2-d 所示),使边坡出现失稳破坏. 软弱夹层边坡的水平应变演化云图与唐等[10]均质坡体堆载产生水平应变的演化过程不用,均质坡体的拉应变是从坡脚处开始发展变化,而当坡体中存在软弱夹层时,荷载产生拉应变率先在软弱夹层中出现,且不断向荷载作用区域发展,然后坡脚处才出现拉应变,且向上与先前产生的拉应变贯通.

图2 条形基础荷载加载中软弱夹层边坡水平应变云图(拉正压负)

2.1.2 边坡不同高程处水平应变及位移分布
图3 为条形荷载加载过程中软弱夹层边坡不同高程处的水平应变分布曲线. 当基础荷载作用的坡顶区域(H6测线)水平应变为压应变,而荷载左右两侧表现为拉应变,尤其是左侧拉应变显著. 边坡压应变和拉应变随荷载的增加而增大,且增长速率随荷载呈指数型增加,荷载为130 kPa、150 kPa和170 kPa 时最大拉应变增长率达164 με /kPa、224 με/kPa和434 με /kPa(图4-a). 在170 kPa 时,荷载左右边界附近(滑弧位置)拉应变达到最大,分别为0.02 ε 和0.012 ε. 上述边坡水平应变分布符合地基破坏的典型模式,由此也可看出,坡顶拉应变突增预示着拉裂缝的形成. 对于坡体中H5~H1测线,条形基础荷载下部坡体表现为水平拉应变. 如图4 所示,当荷载相对较小时,最大水平拉应变随荷载增加增长缓慢;当荷载达到150 kPa 后,最大水平拉应变出现突增变化. 整体而言,坡体的最大水平拉应变随荷载增加呈现指数型增长趋势. 通过比较边坡不同高程处的水平应变分布曲线,发现距离坡顶越远,最大水平拉应变位置由荷载两侧向中部汇合,且以左侧应变为主,然后逐渐向右移动,最大水平拉应变值出现在H6测线坡顶,而在坡体内部最大水平应变值出现在H4测线. 对于H1测线,在坡脚处出现较大范围的压应变区域,主要是由于上部坡体变形对坡脚处形成了挤压作用. 此外,基于有效塑性应变给出的潜在滑动面位置与各测线上最大水平应变出现位置相同,表明软弱夹层边坡在条形基础荷载作用下,可以通过监测边坡最大水平拉应变位置来预测潜在滑动面位置.

图3 条形基础荷载加载中软弱夹层边坡不同高程处的水平应变分布
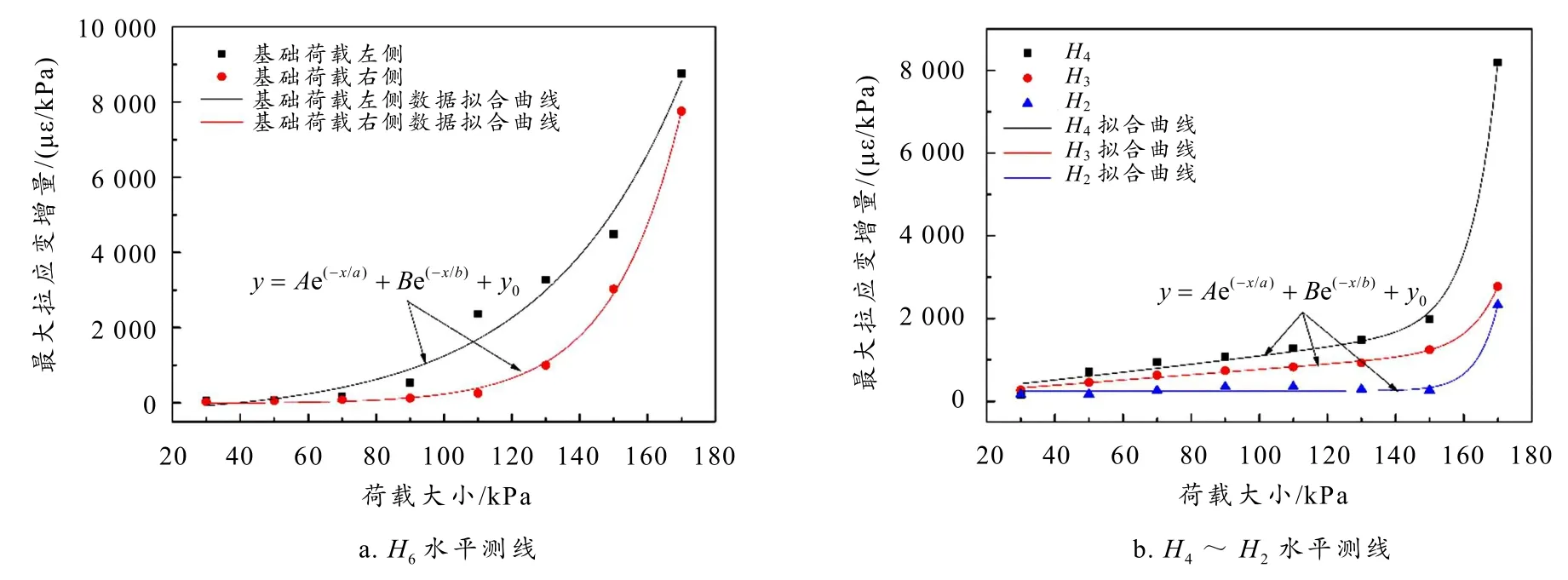
图4 边坡最大水平拉应变增量与荷载的变化曲线
图5 显示了不同位置竖向测线的水平位移分布规律. 对过坡顶的竖向测线1V而言,在边坡中等高程处水平位移较大,且最大水平位移随荷载呈非线性增长,当达到边坡临近失稳破坏的荷载时,水平位移出现突增,边坡破坏时最大水平位移为15.04 mm. 当荷载较小时,最大水平位移位置随荷载增加不断上移;当荷载超过一定值后,位置几乎不发生改变. 此外,软弱夹层边坡最大水平位移出现位置并不与潜在滑动面一致,滑面位于最大水平位移之下,表明滑面上方土体的水平位移大于滑面下方土体. 过荷载加载中心的测线2V也出现类似的变化规律,其区别是在高程9 m 附近出现压缩位移,且2V测线上最大水平位移出现位置高于1V测线,其原因是边坡将出现从左上方坡顶到右下方坡脚的滑动破坏趋势.
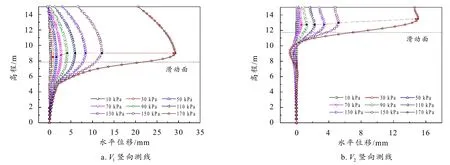
图5 条形基础荷载加载中软弱夹层边坡不同高程处的水平位移分布
2.2 边坡稳定性系数与水平应变的关系
根据上述研究内容可知,边坡的水平应变与其稳定性紧密相关,最大水平拉应变与边坡滑面位置相对应. 此外,文献[3]和[10]研究也表明,边坡水平应变与其稳定性系数之间存在较好的拟合关系,比如对数函数关系等. 因此,研究边坡水平应变与稳定性的关系对预测边坡稳定情况具有现实意义. 对L1=4 m、L2=4 m的条形基础荷载而言,当荷载加载到170 kPa 时,边坡稳定性系数为1.053,模型计算结束,可认为该软弱夹层边坡为极限失稳状态. 利用“边坡稳定(SRM)”求解类型,对不同大小荷载作用下软弱夹层边坡稳定性进行求解.
图6 为不同测线上不同荷载值加载时最大水平应变与边坡稳定性系数的关系,并采用合适的函数对数据进行拟合分析. 如图6 和表2 所示,在下层土体2 中,H1~H3测线上边坡稳定性系数与最大水平应变呈线性变化关系,拟合相关系数R2均大于0.96;而在上层土体1 中,H4~H6测线上边坡稳定性系数与最大水平应变为对数函数变化关系,表明在土层1 中稳定性系数降低时发生的应变更大. 综上表明,该软弱夹层边坡最大水平应变与稳定性系数之间具有很好的拟合关系,但不同土层拟合关系及系数不同,在实际工程中可利用边坡最大水平应变对其稳定性进行评价.

图6 软弱夹层边坡稳定性系数与最大水平应变的关系曲线
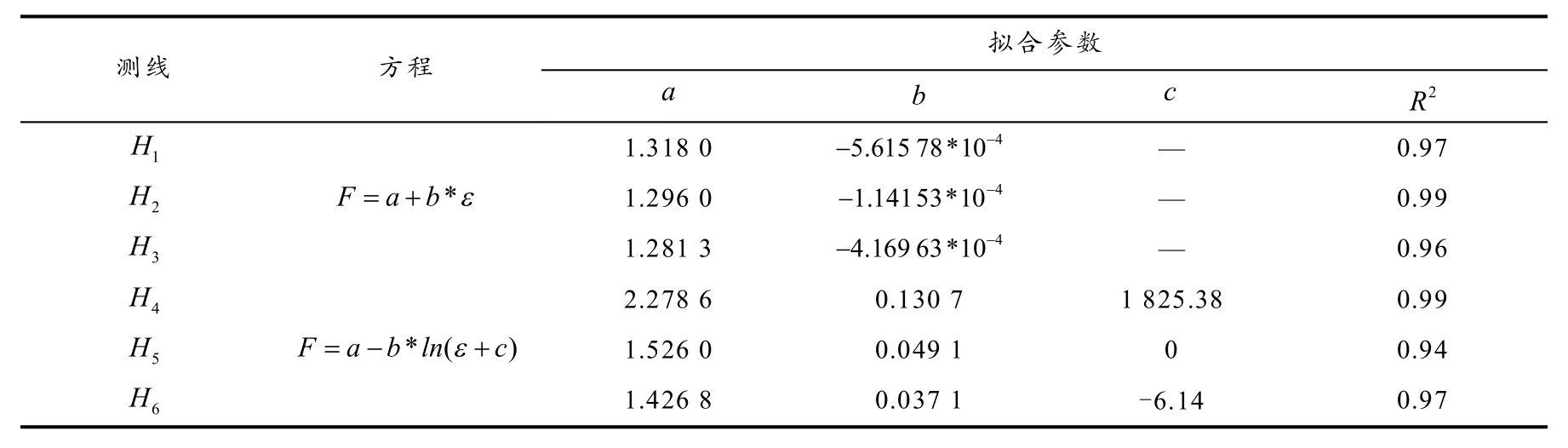
表2 软弱夹层边坡稳定性系数与最大水平应变的拟合参数
软弱夹层边坡稳定性与最大水平应变的关系为:
式中,F为边坡稳定性系数;ε为测线上最大水平应变;a、b和c为拟合系数,与土体参数、荷载形式、测线位置等有关.
3 荷载形式对边坡变形及稳定性的影响
3.1 荷载宽度的影响
当荷载宽度2L为4 m、6 m、8 m 和10 m 时(L1=4 m),边坡发生失稳破坏的极限荷载大小分别为170 kPa、170 kPa、160 kPa 和170 kPa,6 条水平测线上最大水平应变为14 032 με、14 650 με、19 005 με 和19 700 με. 可以看出,荷载宽度对边坡失稳时极限承载能力影响较小,但破坏时的最大水平应变随荷载宽度呈增长趋势. 图7 给出了不同宽度荷载作用下边坡稳定性系数与最大水平应变的关系曲线,发现边坡稳定性系数与各测线的最大水平应变均符合对数变化关系. 综上表明,当荷载距坡顶4 m 时,4 ~10 m 宽度荷载作用下边坡稳定性系数与最大水平应变的变化均符合对数关系,且测线高程越高,对数函数拟合效果越高.
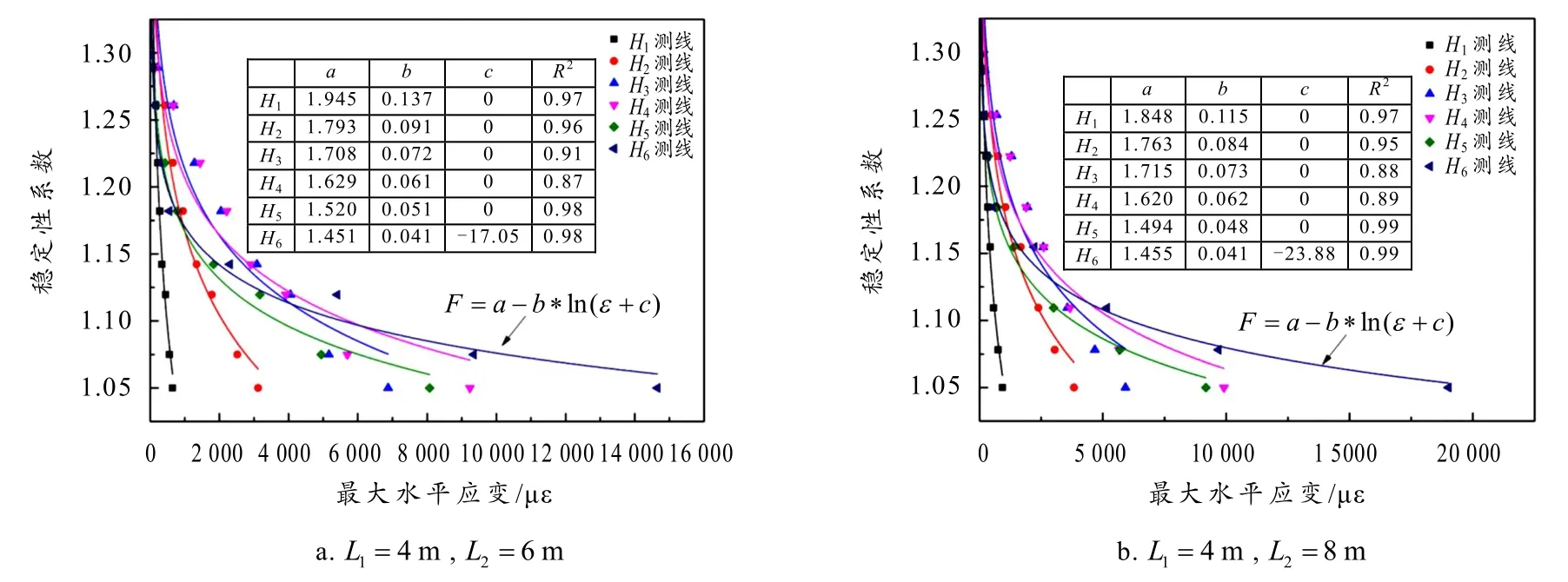
图7 不同宽度荷载作用下边坡稳定性系数与最大水平应变的关系曲线
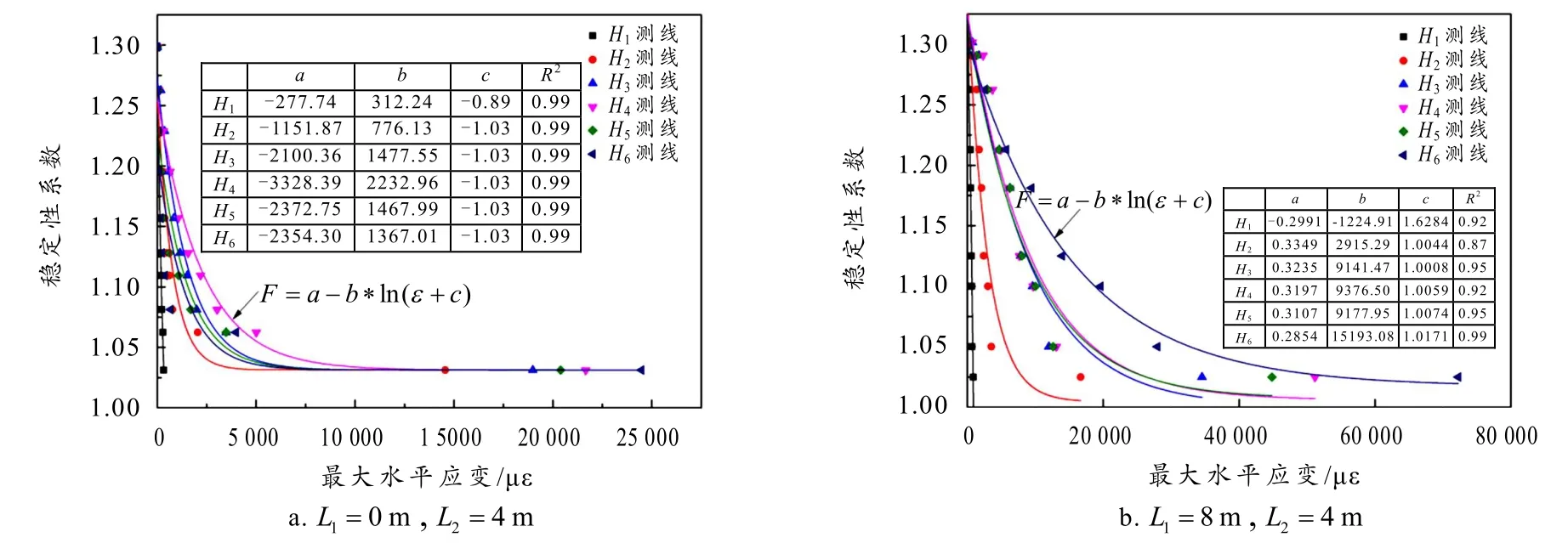
图8 不同位置荷载作用下边坡稳定性系数与最大水平应变的关系曲线
3.2 荷载位置的影响
当荷载距坡顶0 m、4 m、8 m 和12 m 时(L2=4 m),边坡发生失稳破坏的极限荷载大小分别为90 kPa、170 kPa、300 kPa 和420 kPa,6 条水平测线上最大水平应变为24 477 με、14 032 με 、72 269 με 和68 697 με. 当荷载离坡肩越远,边坡极限承载能力越大;当荷载位于坡肩(L1=0 m)或远离坡肩(L1=8 m、12 m)时,最大水平应变均较大,尤其是远离坡肩时,主要原因是边坡潜在滑面为穿过基础荷载左边界和坡脚的曲面,荷载离坡肩越远,滑弧越长,土体随荷载的增加将发生更大的应变. 图 8 显示了距坡肩不同距离荷载作用下边坡稳定性系数与最大水平应变的关系曲线.随着荷载的增加,边坡水平应变增大,稳定性降低;当荷载距离坡肩较近时,边坡稳定性系数与最大水平应变呈对数型变化关系,如L1=0 m、L2=4 m;当荷载距离较远时(L2=8 m),指数型函数更适合,拟合相关系数大部分高于0.92,而对数函数拟合系数多在0.83 以下. 说明软弱夹层边坡的变形及其稳定性与基础荷载加载宽度和位置紧密相关,荷载宽度和位置决定了边坡失稳破坏的极限承载能力和滑面位置,从而改变稳定性系数与最大水平应变的关系,荷载离坡肩越远,边坡发生失稳破坏的荷载越大,使土体产生更大程度的应变.
通过对比分析荷载宽度和位置对稳定性系数与最大水平应变关系的影响,可以发现H5和H6测线的拟合程度最好,意味着实际边坡变形及稳定性分析过程中,应在坡顶附近土体中布置测线对边坡应变进行监测,从而对边坡稳定性情况进行评价.
4 结论
本文对不同形式条形基础荷载作用下软弱夹层边坡的应变分布规律及其与稳定性关系开展了研究,获得主要结论如下:荷载与坡体作用区域为压应变,而其下部一定深度处为拉应变集中区;水平拉应变随荷载增加而增加,且拉应变集中区不断缩小且往上部移动,随后荷载左右边界和坡脚处出现拉应变,形成连续拉应变滑弧致使边坡失稳破坏;边坡不同高程测线上最大水平拉应变随荷载呈指数型增长,其出现位置随测线高程的降低逐渐向右移动,在失稳前发生应变突增,最大水平拉应变为坡顶荷载的左边界;边坡最大水平位移位于滑面之上;上部土层应变大于下部土层,边坡稳定性系数随两者土体中最大水平拉应变的增加分别呈现对数型和线性变化关系,拟合度达0.94 以上;荷载宽度对边坡极限承载能力影响不大,但最大水平拉应变随荷载宽度增加呈增长趋势,且与边坡稳定性系数符合对数关系. 当荷载离坡面越远,边坡极限承载能力越大,土体随荷载的增加发生更大的应变,且边坡稳定性系数与最大水平应变的对数关系逐渐转变为指数关系.
本文在研究不同形式条形基础荷载作用下软弱夹层边坡变形及稳定性问题时,未考虑地震、降雨等工况,当边坡受地震和降雨等影响时其变形特征与稳定性需做进一步研究.

