一种腔室可调的Helmholtz型声子晶体的带隙研究

刘 红,赵静波,姚 宏,韩东海,张晓生,王 晨,张广军

(空军工程大学基础部,西安 710051)

0 引 言

随着我国国防建设的持续推进,一大批高精尖装备陆续装配部队,比如大型飞机、舰艇等。然而密闭舱室内剧烈的噪声不仅会严重影响飞机的使用,还会对内部工作人员的身体健康造成极大危害,从而影响战斗力的有效发挥[1-2]。因此,密闭舱室内的噪声问题亟待解决。目前,解决噪声问题的传统方法主要是在结构中填充吸/隔声材料[3]、敷设阻尼材料[4]等。这些方法能够很好地抑制较高频的噪声,但对于低频噪声的抑制效果并不明显。因此,如何抑制密闭舱室内的低频噪声成为降噪领域研究的难题之一。

近年来,声学超材料的发展与应用为实现大型飞机的低频噪声控制提供了新的途径[5-9]。声学超材料的发展源于局域共振型声子晶体的研究,声子晶体是一种新颖的具有弹性波带隙的人工周期材料或结构[10]。弹性波在晶体结构中传播时,由于受到内部结构的作用会形成特殊的色散关系,这些色散曲线之间的频段称为带隙,位于该频段内的弹性波在结构中传播时会受到抑制而无法传播[11-12]。弹性波带隙一般有两种机制——Bragg散射机制与局域共振机制[13-14]。局域共振型声子晶体在进行弹性波的调控时具有小尺寸控制大波长的效果,使其在低频噪声控制领域具有十分重要的应用价值。另外,局域共振型声子晶体表现出负的等效模量、负的等效质量密度等奇异特性[15-16]。Helmholtz型声子晶体是一种典型的局域共振型声子晶体,该声子晶体由多个Helmholtz共鸣腔作为元胞进行周期排列而成,具有轻质和低频的优势,因此得到了众多学者的认可[17-19]。陈鑫等[20]将Helmholtz共鸣腔与弹性振子结构进行了耦合设计,并分析了带隙隔声特性,研究发现,该结构具有优异的低频隔声效果。Gao等[21-23]研究了含周期性自相似夹杂结构、分形结构以及两个谐振腔的二维声子晶体的带隙特性,结果表明,所设计的结构都具有较宽的低频带隙。Duan等[24]提出通过在六角形蜂窝Helmholtz共鸣腔中引入橡胶涂层来构建一种轻质可调谐声学超材料,实现从100 Hz到300 Hz的可调完美吸收。Rajendran等[25]提出了嵌入式颈部和螺旋式谐振腔,既节省空间,又能实现完美的吸声,提高了整个吸声面板的吸收性能。

目前,在Helmholtz型声子晶体的结构设计中,其带隙频率范围往往是固定不变的,无法根据噪声频率进行精准调控,且低频隔声性能较差。其原因主要有两个方面:一是Helmholtz型声子晶体的结构、腔体布局及开口长度不能改变,导致带隙频率不能根据噪声频率进行调节;二是在该类型的结构中,Helmholtz腔的通道长度有限,无法进一步降低带隙频率。因此,本文从增加开口长度和可调性腔体结构两方面对Helmholtz周期结构进行了优化设计,构建了一种腔体结构可调的Helmholtz型声子晶体。首先,该结构单元采用双开口设计方式,同时在开口处采用弓字形开口通道设计,能够在不增加腔体体积的条件下使开口长度有效增加;其次,通过伸缩螺杆来调整上下两腔的体积,改变带隙频段的位置,从而实现低频带隙频段的可调。为探究低频带隙的形成机理,本文建立了该结构的“弹簧-振子”等效力学模型,并与有限元法进行对比分析。建立该力学模型,不仅可以大幅降低结构设计的难度,而且可以定量分析出结构带隙随结构参数的变化规律,进一步揭示结构参数对低频带隙的影响。

1 声子晶体结构设计及能带分析

1.1 结构设计

本文所设计的腔体可调节Helmholtz周期结构采用弓字形开口的可调节双腔结构,其元胞横截面如图1所示,该结构内腔被活动伸缩螺杆连接的隔板分为上腔和下腔两部分,两腔分别通过弓字形开口的通道与外腔相通。在该结构中,采用弓字形开口通道的设计,增加了空气通道的长度,大幅延长声波在该结构中的传播距离,有效降低了低频带隙的下限。同时,通过调整伸缩螺杆的伸缩长度可以调整两腔的大小,从而改变结构构型,以期达到带隙可调的目的,实现对低频噪声的主动控制。该结构的各项参数如下:正方形框架结构的边长为l,结构管壁和隔板的厚度均为d,开口通道的宽度为s,长度为l1,伸缩螺杆伸出长度为b,上腔、下腔以及外腔的体积分别为V1、V2和V3,晶格常数为a。

图1 元胞横截面示意图Fig.1 Schematic diagram of cell cross section

1.2 周期结构能带分析

本文通过有限元法对该声子晶体的能带结构进行了分析和计算,在Comsol Multiphysics软件平台上构建该模型。由于该模型包含两个区域——空气域与固体域,因此在该软件平台上选用压力声学模块和固体力学模块。本结构中构成Helmholtz共振器结构的材料为钢,其声阻抗远大于空气的声阻抗,从而产生阻抗不匹配现象。当声波由空气向结构内传播时,仅有非常微小的声能量会穿过两者的界面进入结构内部,而大部分声能量会从两者的界面反射回空气中,故设定两者边界为刚性边界。因此,在仿真计算中将该结构视为刚体,仅对空气域进行计算,从而简化仿真计算模型。同时,在结构的上下左右边界处设置周期性边界条件,模拟无限周期结构。根据Bloch理论,采用Bloch-Floquet边界,其表达式如下:

p(r+a)=p(r)eika

(1)

式中:r是位置矢量;a为声子晶体晶格的格矢;参数k为波矢。为了分析该声子晶体的能带结构和共振模态,结构的尺寸参数如表1所示。

表1 结构尺寸参数Table 1 Structural dimension parameters /mm

通过Comsol Multiphysics平台对该结构进行仿真计算。经过计算,该结构的带隙图如图2所示。为了验证能带结构计算的正确性,用有限周期结构的隔声曲线图来进行对比,隔声量如图3所示。

图2 结构带隙图Fig.2 Structural bandgap diagram

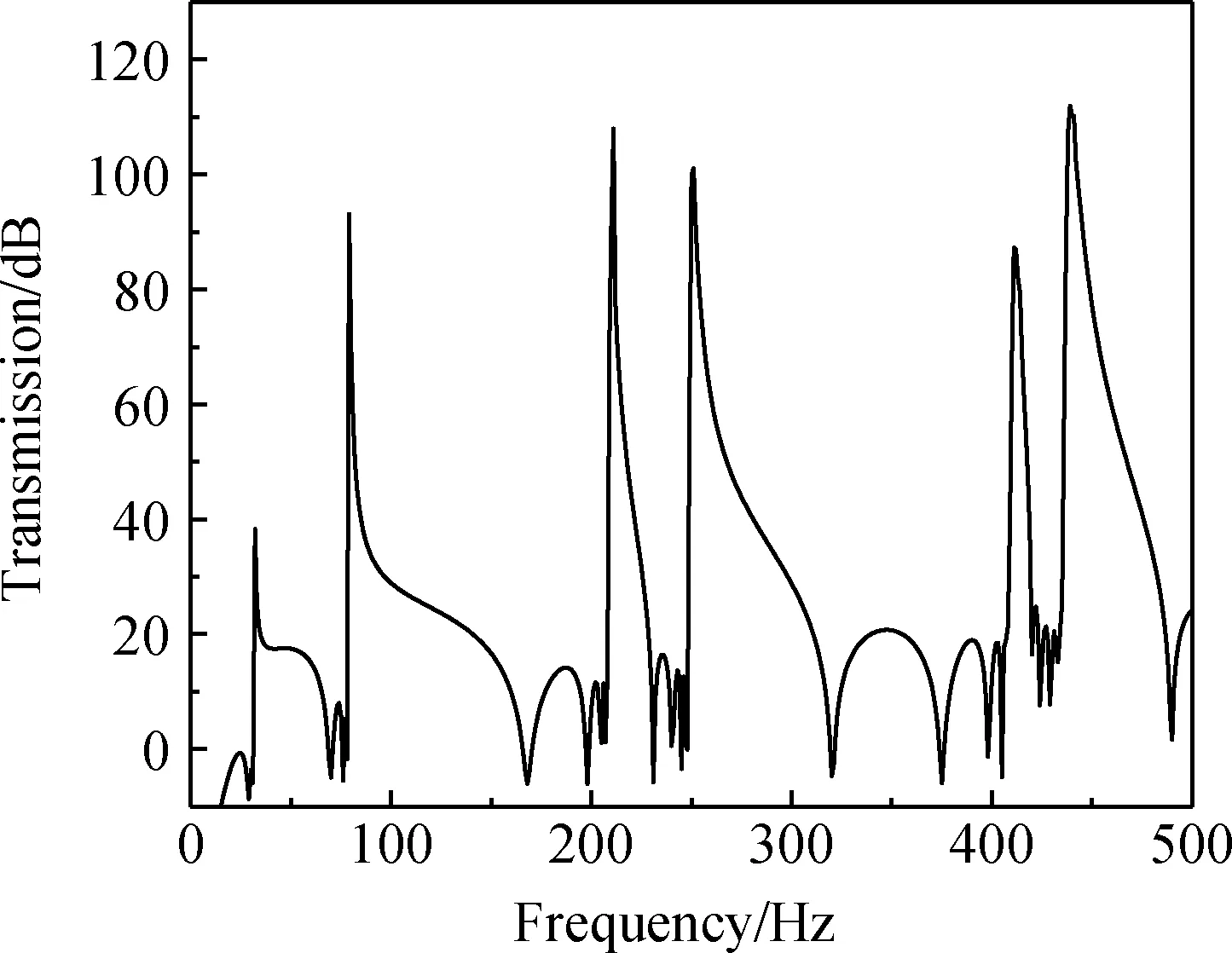
图3 隔声曲线Fig.3 Sound insulation curve

由图2可以看出,该声子晶体结构在0～500 Hz的频段范围内共有6条完整带隙(图2中深灰色部分),其带隙范围分别为31.34～51.79 Hz、79.02～126.53 Hz、210.26～229.18 Hz、250.62～296.21 Hz、412.88～425.78 Hz和439.42～478.39 Hz。同时,该结构将第一低频的带隙下限降至31.34 Hz,有效降低了传统声子晶体的低频带隙下限。由图3可以看出,该结构在500 Hz以下频段范围内共出现6个隔声峰,带隙频段内的声波受到了抑制,隔声效果较好,且声波的抑制范围与带隙频段吻合度较高,证明了带隙计算的正确性。

2 低频带隙形成机理建模分析

2.1 带隙机理研究

为进一步揭示该结构(结构尺寸参数如表1所示)带隙产生机理,探究其低频隔声特性,针对该结构的第一、二带隙上下限的声压场进行分析,如图4所示。

由图4(a)可知,声压几乎全部局限在下腔,上腔和外腔声压场几乎没有压力。此外,在下腔开口通道内的声压呈现梯度变化,由内向外逐渐减小。该现象说明此处出现局域态,声波的振动局限在下腔中。因此,声波无法继续传播,此时第一条带隙被打开。

由图4(b)可知,第一带隙的上限声压场与下限声压场有较大不同。从图中可以看出,声压在结构内腔和外腔均有分布,上腔的声压高于下腔声压,且上下腔声压相位相反。表明结构不能隔绝声波的传播,第一带隙截止。

采用相同分析方法,如图4(c)所示,第二带隙下限处的声压场与第一带隙下限处声压场相似,呈现出局域共振态。但与第一带隙不同的是,此时下腔和外腔处声压场压力接近于0,声波被局限在上腔中。并且,在上腔的开口通道内,声压场呈现出梯度变化规律,由内向外逐渐减小。表明第二带隙下限处出现与第一带隙下限处相似的模态,此时第二条带隙被打开。

图4 带隙上、下限声压场Fig.4 Upper and lower limit sound pressure fields of the first and second bandgaps

如图4(d)所示,第二带隙上限处声压分布于结构的内腔和外腔,下腔与上腔声压相位相同,且上腔声压高于下腔声压。表明声波能够在结构外部与内部正常传播,此时第二条带隙截止。

通过上述分析,可以得出如下结论:该结构由于内外腔共振可以打开多条带隙,将声波局域于结构内部,阻止声波传播;带隙的打开与内腔具有高度联系,第一带隙起始频率主要是下腔共振的结果,而第二带隙起始频率则是上腔作用的结果;当外腔空气层与内部结构共同作用时,带隙截止。

2.2 等效模型的建立

为了进一步揭示带隙产生机理,建立该结构在带隙上下限处的“弹簧-振子”等效模型,通过等效模型对该结构的带隙上下限进行计算。

为了建立该结构的等效模型,将元胞结构划分为5部分,分别为外腔、下腔、下腔通道、上腔,及上腔通道,并对该Helmholtz腔作如下假设:

1)弓字形通道体积远远小于上下腔的体积;

2)该元胞结构的线度远远小于低频声波的波长;

3)腔壁为刚性腔壁,在内腔中空气压缩和膨胀时,不发生形变。

对于弓字形通道中的空气,由于弓字形通道的体积远小于腔体的体积,故可认为开口通道中的各部分空气在振动时是相同的,该部分的空气可以看作在开口通道内振动的振子,上腔通道和下腔通道两部分空气等效振子的质量分别为m1和m2,其表达式为:

m1=m2=ρal1s

(2)

式中:ρa为空气密度;l1为上腔通道或下腔通道的长度;s为上腔通道或下腔通道的宽度。

对于上腔、下腔和外腔中的空气部分,当上腔通道和下腔通道中的空气在通道内发生振动时,由于腔壁不发生形变,因此上腔、下腔和外腔中的声压会随着通道内空气的振动而发生压缩和膨胀,此时各腔内的空气可看作空气弹簧。其等效刚度分别为k1(上腔)、k2(下腔)和k3(外腔),其表达式分别为:

(3)

(4)

(5)

式中:V1、V2和V3分别为上腔、下腔和外腔的体积;c为空气中声速。

结合第一、二带隙上下限处各点的声压场,对各点处的振动模态进行分析,并建立对应的等效模型。对带隙下限处的声压场分析可知,第一、二带隙下限处的振动模态相似。如图4(a)所示,第一带隙下限处外腔、上腔和上腔通道的声压场几乎为0,因此可忽略外腔、上腔和上腔通道中空气的作用,只考虑下腔、下腔通道两个区域。根据声力类比原理,狭长通道可以等效为振子,而下腔的空气可等效为空气弹簧,其构成的“弹簧-振子”模型如图5(a)所示。同理,如图4(c)所示,第二带隙下限处外腔、下腔和下腔通道的声压场为0,因此可忽略外腔、下腔和下腔通道中空气作用,故此时构成的“弹簧-振子”模型如图5(b)所示。

图5 带隙下限等效模型Fig.5 Equivalent model of lower bandgap

在上述等效模型中,第一、二带隙下限fdown1和fdown2的表达式分别为:

(6)

(7)

对于带隙上限处的振动模态,如图4(b)、(d)所示,外腔、下腔、下腔通道、上腔和上腔通道五个区域都具有声压分布,因此在对带隙上限处进行模型等效时,外腔、上腔和下腔空气等效为空气弹簧,而上腔通道和下腔通道中的空气等效为振子,因此其构成的“弹簧-振子”模型如图6所示。

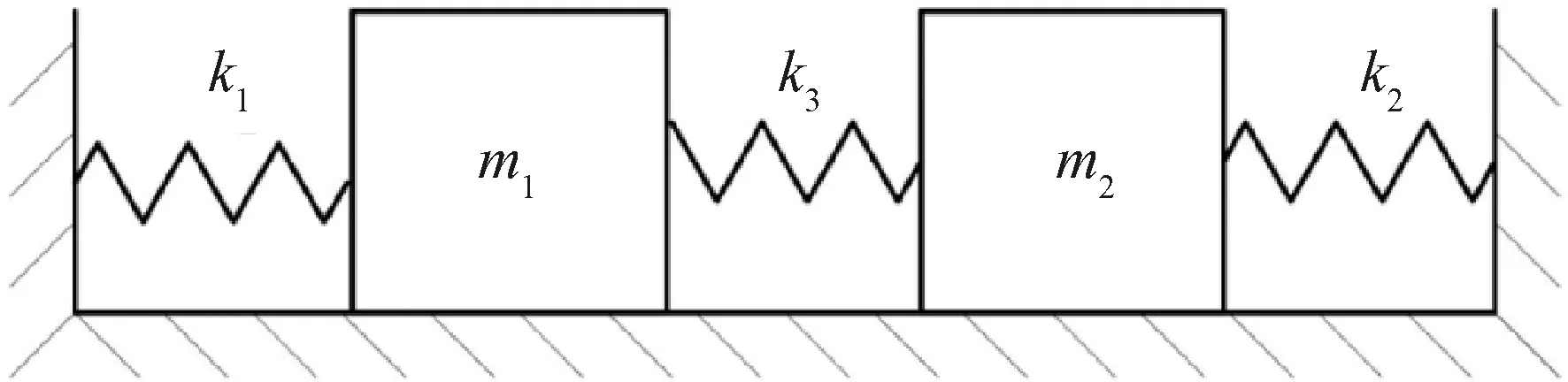
图6 第一、二带隙上限等效模型Fig.6 Equivalent model of the first and the second bandgaps upper limit

根据上述模型,构建其刚度矩阵表达式为:

(8)

振子的质量矩阵为:

(9)

根据多自由度系统的振动理论,第一、二带隙的上限fup1和fup2表达式为:

(10)

通过等效模型的方法推导出该结构带隙的计算公式,其计算结果与仿真实验计算结果误差较小,证明了计算公式的正确性。同时,通过两种方法计算得到的结果之间的误差主要来源如下:在仿真实验中,当伸缩杆伸出长度b为25 mm时,上腔的体积较小,因此,开口通道不再是体积远小于内腔的细管道,使得Helmholtz腔“声力类比”的假设条件弱化,从而导致出现误差。

3 低频带隙影响因素分析

通过对结构的低频带隙形成机理进行分析,注意到其低频带隙起始频率主要受上下腔布局的影响。当调整上腔、下腔的大小,即调整伸缩杆长度时,其结构将发生改变,从而改变协同共振区域,影响带隙结构。而带隙的截止频率与外部空气层有关,即结构排列空隙间隔。因此对伸缩杆长度、结构排列空隙间隔这两个因素进行分析,研究其对低频带隙结构的影响。

3.1 腔体结构对带隙影响

在分析双腔可调局域共振结构的伸缩杆长度对低频带隙的影响时,取结构参数a=61 mm,l=60 mm,s=0.5 mm,l1=847.5 mm不变,伸缩杆长度b由25 mm减小到0 mm,计算出其带隙结构变化如图7所示。

图7 内腔不同构型情况下带隙结构图Fig.7 Bandgap structure diagram with different configurations of inner cavity

从带隙产生的机理可知,第一带隙主要是下腔与其开口通道局域共振的结果,而第二带隙则是上腔与其开口通道局域共振的结果。通过对图7伸缩杆的不同伸缩长度的能带图分析可知,当伸缩杆从25 mm减小到0 mm时,上腔体积不断增大,下腔体积不断减小,上腔的增大使第二带隙不断下移,下腔减小使得第一带隙缓慢上移。当伸缩杆伸缩长度为0 mm时,两腔体积相等,第一带隙和第二带隙合并为一个带隙。从总体上看,第一带隙在伸缩杆变化过程中小幅度变化,但第二带隙在伸缩杆长度不断减小的情况下,带隙不断下移,覆盖了较大低频段。在工程应用中,该结论对于噪声波峰进行特定消除具有良好的适应性。

为进一步研究这种结构的适应范围,本文分析了在可调板变化后,结构的第一、第二带隙变化情况,如图8所示。伸缩杆长度从25 mm到0 mm的变化过程中,内腔结构发生变化,导致带隙结构发生变化。由图8可以看出,随着伸缩杆长度的减小,第一带隙的宽度逐渐减小,同时第一带隙的下限值在不断增大。相反,对于第二带隙来说,其宽度在不断增大,并且第二带隙的下限值在不断减小,从整体上看,两条带隙在可调板移动的过程中不断趋近,最终合为同一条带隙。

3.2 结构单元间隔对带隙的影响

本文分析了双腔可调局域共振单元结构排列间隔对低频带隙的影响,取结构参数b=25 mm,l=60 mm,s=0.5 mm,d=0.5 mm,l1=847.5 mm不变,晶格常数a由61 mm增加到70 mm。通过分析计算,得到周期排列间隔对带隙结构的影响如图9所示。

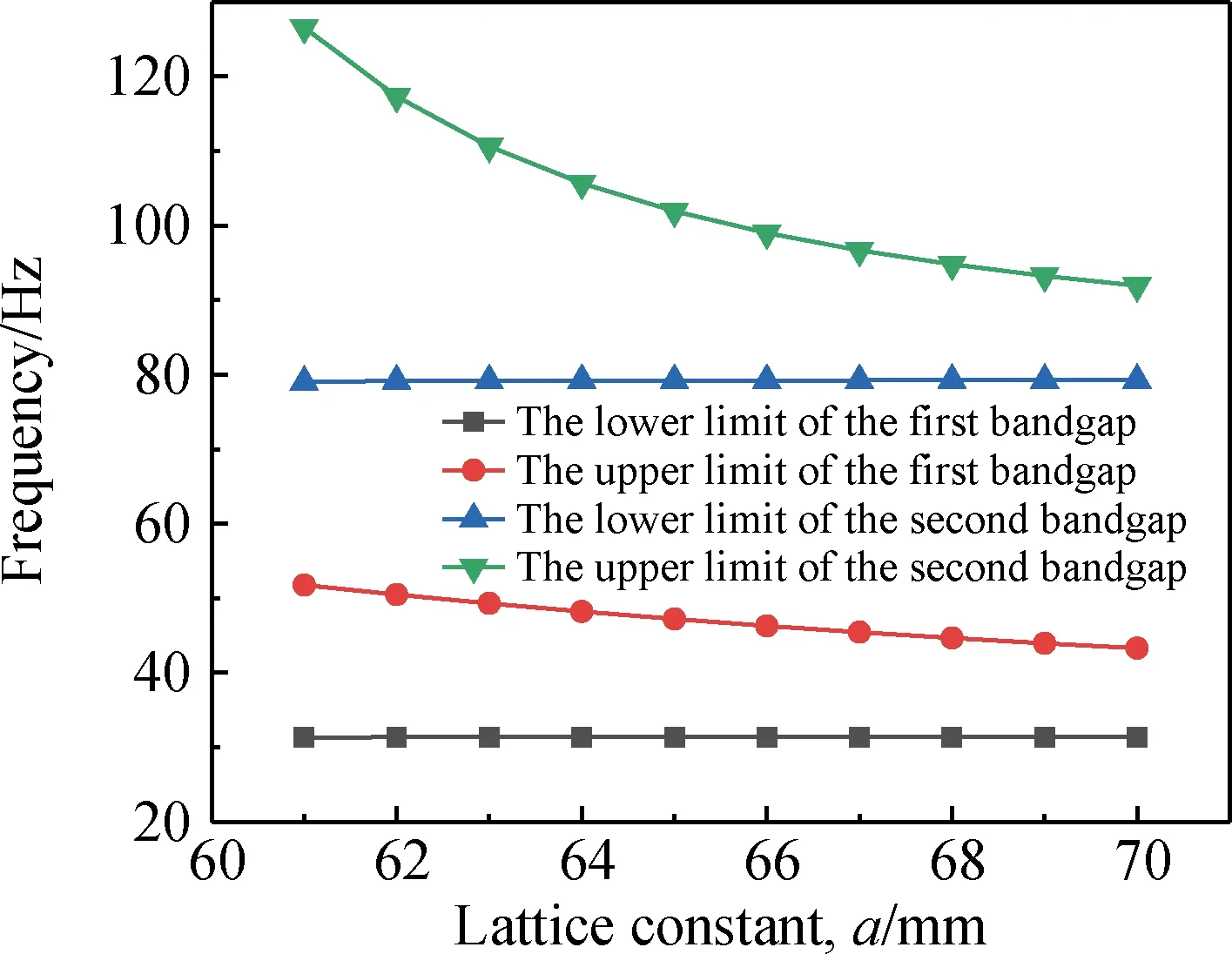
图9 晶格常数对带隙的影响Fig.9 Impact of the lattice constant on bandgap

图9结果表明,针对本文所设计的结构,当其他参数不变,只改变晶格常数时,第一带隙和第二带隙的下限基本不受影响,而带隙的上限随晶格常数的增加而减小(第一带隙上限由51.78 Hz变为43.33 Hz,第二带隙上限由126.53 Hz变为91.95 Hz)。对于带隙上限的减小,其原因在于当正方形框架结构的边长不变时,随着晶格常数的增加,外腔的等效刚度k3减小,从而导致带隙的上限下移。因此,第一带隙和第二带隙的宽度都大幅减小。由以上分析可以得出,保持较小的排列间隔是增加该结构低频带隙宽度的一种有效方法。

4 结 论

本文利用影响Helmholtz周期结构带隙和隔声特性最重要的两个因素——开口深度和腔体结构,设计了双开口通道的腔体可调节的Helmholtz周期结构。通过仿真计算、理论推导等方式进行了相互验证,结果表明,该结构具有良好的低频隔声特性,并可以根据噪声环境调节结构达到特定频段的隔声效果。同时,讨论了该结构的结构参数对低频带隙特性的影响,研究表明经过合理设计的两个腔体,能够得到多条低频带隙,并且通过调整腔体布局、大小等方式可以将多条共振带隙相连而拓宽带隙。另外,在Helmholtz结构周期排列设计中,采用较小的单元间隔,合理利用局域共振双耦合机制,也可以大幅提高带隙的范围,能够达到在较大频率范围内隔声的目的。