基于最小约简的粗糙集数据挖掘算法研究*

杨晓波

（浙江树人学院 杭州 314408）

1 引言

近年来，粗糙集理论在数据挖掘领域的应用日益广泛。Christie 等［1］提出了利用粗糙集实现数据弹性变化的方法，但未解决数据规则随条件变化的问题；Y.Zhang 等［2］提出了粗糙集的决策表生成算法，但没有降低粗糙集的时间复杂度；Raghuwanshi等［3］提出了模糊理论与粗糙集相结合，但关联规则的生成较复杂；Fetouh 等［4］提出了在粗糙集中引入遗传算法，提高了运算效率，但也带来一定的误差；G. H. Zhang 等［5］提出在关系数据库中引入粗糙度模型，数据的检索效率有所提高，但并未降低计算复杂度；Choubey 等［6］通过采用递推算法确定关联规则，但对多维度的数据挖掘效率较低。随着数据分析和挖掘技术的不断改进，传统的粗糙集理论已经越来越不适应新形式的需求，也暴露出数据挖掘效率较低、算法单一、误差较大等问题。粗糙集理论虽然能够分析隐藏在数据中的事实且不需要提供数据的附加信息，但在实际应用中，还需要处理数据中的噪声和有效计算等问题。因此，需要寻求有效的约简算法以扩展经典粗糙集理论。本文提出一种基于最小约简的粗糙集数据挖掘算法，优化改进传统粗糙集在数据挖掘领域应用的不足。

2 算法原理

约简算法在数据挖掘领域，用于在原始数据集中发现最小子集，并将数据进行分类。相关学者通过分析数据的内在关联提出了几种主流约简算法。Connolly等［7］提出利用属性值获取最小约简的方法，但计算准确度较差；Y.He 等［8］利用深度层次聚类算法计算最小约简，计算的准确度有所提高，但耗时较大；B. Xu 等［9］提出以区分矩阵为基础获取最小约简，运算效率进一步提高，但生成规则较复杂。本文将在总结专家学者研究的基础上，提出一种基于粗糙集理论的优化约简算法。

该算法以属性特征为基础，利用其在区分矩阵的出现次数构造生成规则，通过计算获得最小约简。由于约简与区分矩阵之间存在一定联系，在算法设计时应予以考虑，具体的算法设计流程如图1所示。

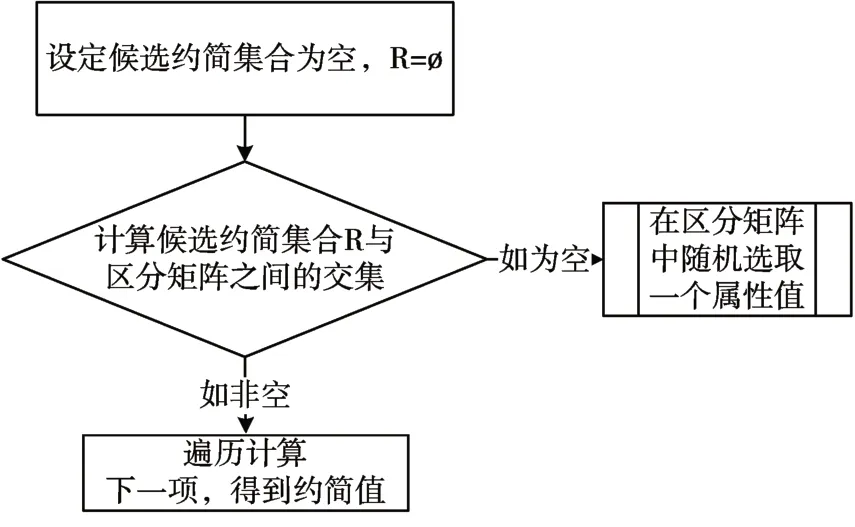
图1 优化约简算法流程图

从图1 得到的约简值，不一定是最小约简，要获取最小约简需要制定相应的约简生成规则。

制定生成规则首先将区分矩阵成员c 进行排序，然后计算每个成员项的属性值，区分矩阵的属性值唯一，则成为约简候选成员；另外还需计算区分矩阵成员的长度和频率，一般长度与频率成正比，长度值可以通过计算成员属性的加权平均值获得，频率值可通过计算成员属性的加权求和获得。

区分矩阵成员的属性值每计算一次，便更新一次属性频率，属性频率的表示如下：

其中p(a)表示属性频率函数，N表示满足条件的属性个数，c表示区分矩阵的成员项。

从式（1）可知，属性频率与属性个数N 成正比，与每个成员项的属性值成反比。属性频率值越大，当计算区分矩阵的成员项时，越有可能得到最小约简。

为了清晰表达如何通过生成规则获得最小约简，算法的实现流程如图2所示。

从图2 可知，区分矩阵是计算最小约简的基础，通过计算成员项的属性频率来建立生成规则，并从属性频率中找到频率值最大的属性，以确定最小约简。利用生成规则可以大概率确定最小约简，即使没有获得最小约简，也会获得次优约简，同时降低算法实现的复杂度。

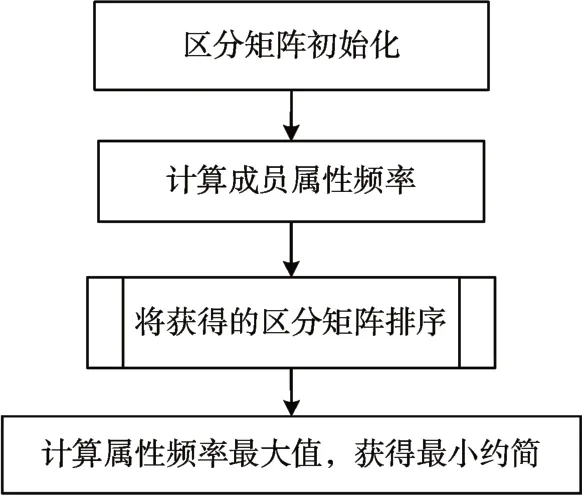
图2 利用生成规则获得最小约简

3 扩展模型

约简算法在实际应用中，经常面临噪声干扰、数据不完整等问题，为了解决这一问题，我们采用在粗糙集中引入扩展模型。

引入扩展模型目的是提升约简粗糙集的抗干扰能力，提高获取最小约简的准确度。本文提出一种精度可变的粗糙集扩展模型，当数据集中的数据变化较剧烈时，可以通过改变精度降低误差。

通常模型的分类误差有一定范围，一般小于5%，可以利用可变精度参数α(0 ≤α≤0.5) 来表示。

假设集合A 与集合B 均为论域U 的非空子集，我们利用式（2）表示约简算法的扩展模型。

当集合A 与集合B 中的元素存在一一对应时，分类误差的概率小于α。当α=0 时，说明集合B包含集合A；当α≠0 时，说明集合A 与集合B 存在一定的近似关系。

集合A 的下限一般表示集合元素在集合A 的分类误差小于α，与之相对应，集合A 的上限通常表示集合元素在集合A的分类误差大于α。

借助集合的下限特点，我们可以定义属性之间的近似关系，这种近似关系以可变精度参数α为基础，通过计算分类误差来评测可变精度参数α的分类能力。需要说明的是，近似分类有别于传统的粗糙集分类，传统的粗糙集以精确度为分类基础，更多地依赖于函数特性。

可变精度扩展模型与传统粗糙集模型可以做到相互兼容，我们可以将可变精度参数α近似看作约简的最小子集，当α=0 时，可变精度扩展模型便等价于传统粗糙集模型，因此可变精度扩展模型继承了传统粗糙集模型的基本特性，因而适用面更广。

当数据集元素的属性值缺失，传统粗糙集模型的分类误差将增加，这时，我们借助可变精度扩展模型的近似关系，降低分类误差，提高数据分类的准确度。

当使用可变精度扩展模型的近似关系区分数据类型时，相似类与原集合存在部分重叠，且相似类不再用于区分数据类型，我们可以利用相似集S(x)来划分原集合。

式（3）中S(x)表示元素与属性集合B 之间的相似度，相似集S(x)并不代表决策类，为了确定决策类集合，我们可以借助相似集S(x)定义决策类。

集合B 包含于论域U 之中，如U 中的任意元素存在与集合B 中元素相似，则说明两个集合的决策值是相同的。相似关系的属性约简算法过程表示如图3所示。

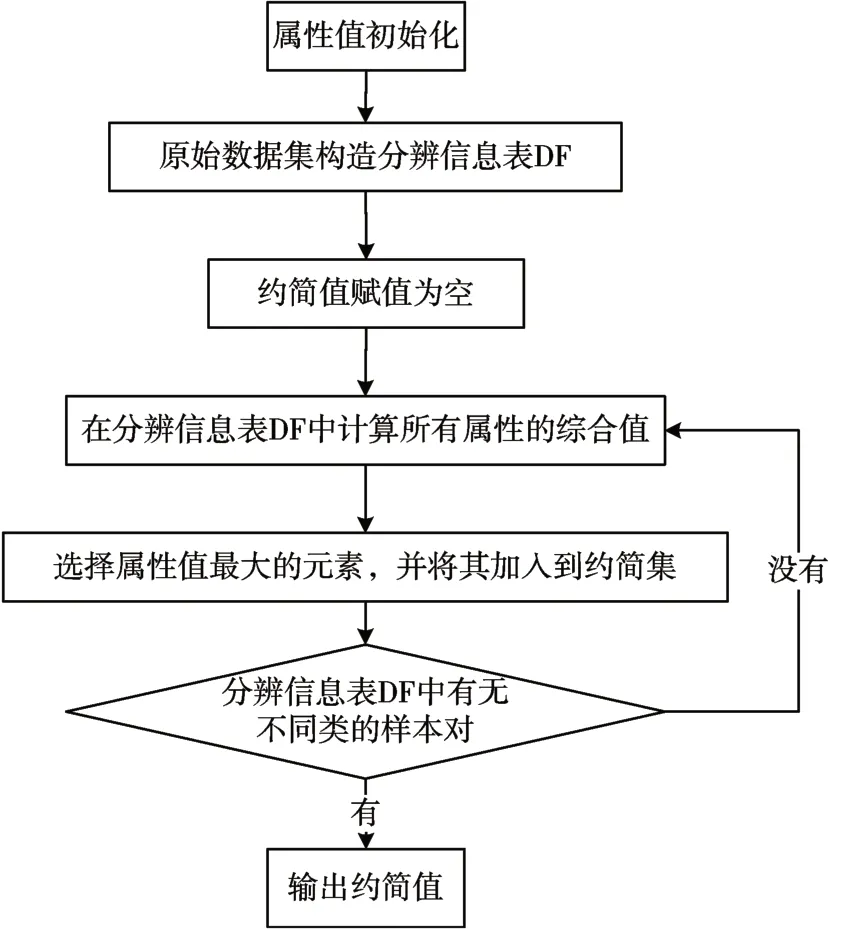
图3 相似关系的属性约简算法

从图3 可知，属性约简首先初始化属性值，再从属性集合中选取最大值，并将属性加入到约简集中，最后在信息表中查找不同类型的样本对，并输出约简值。

在此算法中，分辨信息表DF 用于评价属性在对象类中的相似性，与传统分类矩阵相比，该表增加了同类样本的属性差异值，因此，评价属性特征时，可以从同类样本的相似性和不同类样本的相异性两方面衡量。分辨信息表DF的定义如下：

其中论域U={x1,x2,…xn} ；

条件属性C={c1,c2,…cm} ；

决策属性D={d1,d2,…dn} ；

属性值域V=[0 ,1] ；

信息函数f=U×C。

4 实现过程

区分矩阵往往占用的空间较大，甚至比原始数据集还要大，为了节约存储空间，可以用0或1表示区分矩阵每项的属性，当值为0 时，表示该项不存在属性，不需要存储；当值为1 时，表示该项存在属性，这时才需要存储，这样就可以节约大量存储空间。

最小约简的粗糙集数据挖掘算法，实现过程如图4所示。

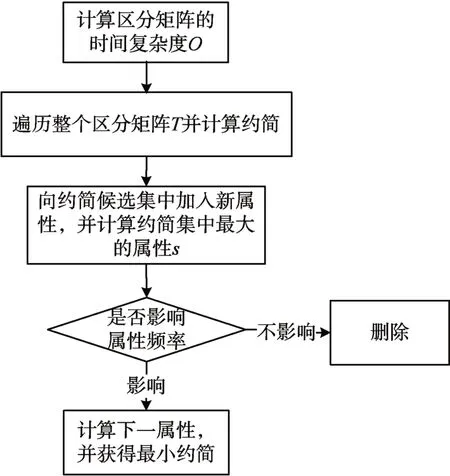
图4 最小约简算法的实现过程

另外，借助区分矩阵的生成规则约简算法表述如下：

输入：区分矩阵T

输出：约简集合

Begin

初始值Red=φ

计算区分矩阵T 并同时计算每项的属性频率p(ai),i=1,…n；

5 实验分析

为了检验本文所提算法的可靠性，拟采用40个数据集进行测试，测试环境是：硬件平台，Intel Core i6-4790 4.5GHz CPU，IntelG51 Express Chip⁃set，8GB DDR3 Ram；软件平台，Visual Studio 2010，数据集采用具有连续属性的数据集，首先利用熵方法对数据集进行离散化，然后利用区分函数方法［11］计算数据集中的所有约简，最后借助本文算法找出数据集中的最小约简。同时采用RSL 算法进行对比，分析两种算法的优劣性。

经过计算，在40个数据集中，有17个数据集存在唯一约简，两种算法均能成功找到这些约简，它们都是由长度唯一的区分矩阵组成；另外，有5 个数据集无法计算所有约简，说明不是每个数据集都存在唯一约简。实验数据集的基本特性如表1 所示。

表1 数据集的基本特性

以数据集Forest 为例，介绍利用约简算法找到约简的过程，为简单起见，属性名采用整数进行编码。

RSL算法找到的约简如下：

本文算法找到的约简如下：

两种算法都找到了最小约简：（0 1 3 5 9 10 11）。

对于数据集Connect 1，RSL算法找到的约简如下：

（0 1 2 5 6 10 13）；（0 1 3 5 6 11 15）；（0 3 2 5 7 10 17）

其中最小约简为（0 1 2 5 6 10 13）。

本文算法找到的约简如下：

（0 3 2 5 6 12 15）；（0 3 1 5 7 10 17）；（0 1 2 5 6 10 13）；（0 3 2 5 6 11 18）；（0 1 3 5 6 10 13）

本文算法所得到的最小约简超集为（0 1 2 5 6 10 13）。

对于数据集Food，两种算法所得到的约简均为

其中第2 个约简，本文算法得到的是一个次优解。

从表1的数据比较中，可以得到如下结论：

1）在大多数情况下，两种算法都能找到最小约简。本文所用算法有16 个数据集表现比RSL 好，RSL在两个数据集中超过本文算法。

2）两种算法在执行实例数较小的数据集时，运行时间比较接近，当在实行实例数较大的数据集时，本文算法的时间复杂度较低，而且运行时间也少于RSL算法。

3）对大多数数据集而言，较短的时间内就可以求出所有约简，约简算法的执行时间取决于两个主要因素，即实例数及核的长度，当核较大时，约简计算相对简单，同时产生的约简个数也较少。

存在唯一约简数据集的计算结果如图5所示。

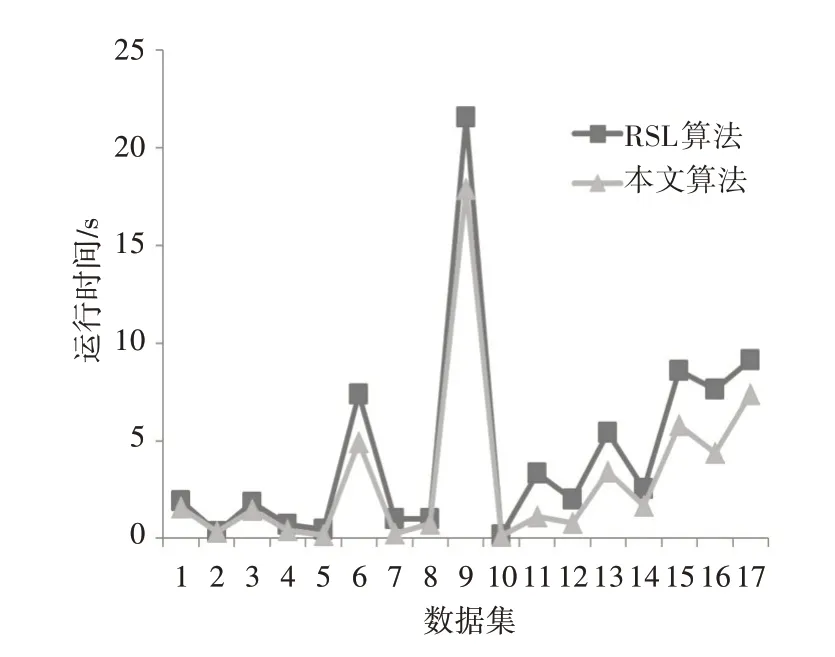
图5 两种不同算法效率对比图

从图5 可知，17 个数据集中，RSL 算法的运行时间均超过本文所提算法的运行时间，前者的平均运行时间比后者多出近30%，换言之，本文所提算法的运行效率优于RSL算法。

6 结语

本文提出一种基于约简粗糙集的数据挖掘算法，通过算法分析和对比性实验得出以下结论：

1）利用区分矩阵中项的长度和属性频率信息，制定启发规则，并从中寻找最小约简，在大多数情况下，可以找到最小约简，即使找不到最小约简，也会找到次优约简，且算法复杂度较低。

2）采用精度可变的粗糙集扩展模型可以提升粗糙集的抗干扰能力，同时能够提高获取最小约简的准确度。为了客观评价属性在对象类中的相似性，提出相似关系的属性约简算法。

3）为了验证本文所提算法的可靠性，采用40个数据集进行对比性实验，结果表明：本文所提算法的运行效率高出其他主流算法近30%。

4）今后的研究方向包括开发更有效的属性频率加权机制，进一步降低本文所提算法的复杂度等。