结合ACGAN 和多重多维混沌系统的无载体信息隐藏*

孙 昊 姜子豪 郝晨茜 石 慧

（辽宁师范大学计算机与信息技术学院 大连 116033）

1 引言

近年来，无载体信息隐藏方法通过结合各种生成式对抗网络（Generative Adversarial Networks，GAN）达到了较好的信息隐藏的效果。周琳娜［1］提出了一种基于GAN 的无载体信息隐藏方法，由噪声作为驱动来产生图像样本，当输入噪声后GAN就可以输出随机的特定图像，信息隐藏则是将秘密信息作为噪声的替代，便可以进行以秘密信息为驱动的无载体信息隐藏。文献［2］提出一种基于生成对抗网络（Improved Wasserstein GAN）的信息隐藏，利用网络的特点对方法进行了改进。文献［3］利用ACGAN（Auxiliary Classifier GAN）［4］，将秘密信息作为类别标签，与随机噪声作为驱动因素相结合，生成标签对应的特定图像，从而实现无载体信息隐藏。

上述算法对于信息安全性考虑不多，本文将ACGAN与多重超混沌系统、DNA加密有机结合，提出了新的无载体信息隐藏的方法。ACGAN 相较于原始GAN 和其它派生GAN，它的特点兼优点是采用了辅助分类器，使得生成图像可被设定的标签进行分类，以增强生成器。本文正是反向利用该特点，通过分类获得图像标签，最后用标签还原出秘密信息以达成无载体信息隐藏。本文以新四维超混沌系统为基础，对原始图像进行复合置乱、DAN加密，再将秘密图像作为类别标签对ACGAN 进行训练，结合排序拼接成组合图像并进行加密，最后将训练后的ACGAN 与加密图像集一同进行发送，接收方通过该ACGAN得到相应的图像信息。

2 相关知识

2.1 多重新超混沌系统

新超混沌系统作为一种基于数字信号的新型加密算法被应用于图像加密中，该方法的初始灵敏度高，随机性好，并且有多个利雅普诺夫指标，具有良好的保密性能，在实现加密算法时可以提供巨大的密钥空间。

本文使用了两种不同的四维新超混沌系统叠加而成的多重新超混沌系统来进一步提升安全性。相比于其它新超混沌系统加密算法而言，本文所使用的两种新四维混沌系统较为新颖、简单且更容易实现。其综合性能良好，迭代后的随机性较好。

本文使用的第一个混沌系统数学模型为式（1）所示：

其中a,b,c,d,m,f,g,r为实常数。当参数a=20.5,b=68.8,c=42,d=5,m=4,f=4.5,g=5,r=20 时，系统存在一个典型的混沌吸引子［5］。

第二种新四维超混沌系统的数学模型如式（2）如下所示。其中，当a=24，b=25，c=3 及d=0.5 时，系统处于混沌状态。该算法的密钥敏感度很高，将其与第一种混沌系统交替使用可有效增加混沌序列的复杂性及敏感性。

2.2 DNA编码与解码

DNA 加密具有加密容量大，对系统性能占用比率较低，可被广泛应用等特点。其中A 与T 是互补的，同样G与C也是互补的。将四个碱基分别编码为00、01、10、11 时，共可以产生二十四种编码方案。但满足Waston－Crick互补规则的只有其中八条，如表1 所示。在DNA 算法快速发展时期，研究者同时为DNA序列构建了基因算法，如表1 所示。

表1 DNA 编码和解码规则

2.3 ACGAN

GAN 是一种基于二人零和博弈思想的无监督模型，其作用是能生成不存在于真实世界的数据，ACGAN（基于辅助分类器生成对抗网络）是在GAN的基础上派生出的新模型，它的构造与GAN 相似。该模型的生成器不但能够产生特定特性的图像，也能将判别器的损失函数进行优化，从而提高整个对抗网络的精准度。其原理示意图如1 所示，其中G为生成器，D为判别器。

图1 ACGAN原理示意图

ACGAN 使计算机拥有了能够模仿现有数据从而生成独特数据的能力，并增加了模型的类别，其应用广泛，对于实现无载体信息隐藏具有重要意义。

3 图像加密

本文利用新四维超混沌系统为基础对原始图像进行复合置乱加密和DNA 加密，得到秘密图像，加密的流程图如图2所示。

图2 图像加密流程图

3.1 新四维超混沌系统的生成

原始图像P 的长为l，宽为h。将原始图像矩阵P'作为哈希函数的初始参数，利用MD5算法生成一段长度为32位的十六进制信息摘要密钥序列Q，生成公式如式（3）所示。

索引序列Q 均分为四个部分，分别通过式（4）中得到x，y，z，w四个新超混沌系统的初始参数。hex［］是生成固定长度十六进制序列的哈希函数，hex2dec()的作用是将生成的序列从十六进制转换成十进制序列。

将式（4）中得到的初始值X0,Y0,Z0,W0代入新4 维超混沌系统中，迭代N 次。其中N=(l×h/3)mod 8。

新4维超混沌系统的模型如式（5）所示：

迭代后的X′，Y′，Z′，W′即作为混沌系统中的四维。

3.2 图像复合置乱

3.2.1 位置置乱

Step 1. 将图像P进行分块；

Step 2.以第一个块作为初始块，每次将以前一块为顶点，以i×i(i=1,2,3,4…) 大小子块为单位，进行块旋转θ度，其中θ=(l'mod 3+1)×90°，得到置乱后的图像P1，其中l'为图像分块后每一行的块数。

3.2.2 像素置乱

将图像P1代入式（6）中，得到灰度置乱图像P2。

其中，n为图像P1的灰度值，n'为图像P2的灰度值，X 为新四维超混沌系统中的第一维。再将灰度置乱与位置置乱进行复合置乱。

3.3 DNA编码与解码

在灰度图像中，每个像素点采用8 位二进制表示后可以按照DNA 编码规则转换成一个对应的四位DNA序列。

步骤1 取出迭代后的新四维超混沌系统中的第二维Y′序列和第三维Z′序列，并根据行列选择不同的DNA规则，

步骤2 由(l+h+y′)mod 8 得到该像素块使用的编码规则，由(l+h+z′)mod 8 得到使用的解码规则。

当DNA 编码和解码只选择单一的规则时，会导致图像灰度值变化较少，所以对不同行列的灰度值使用不同的规则进行变换。

3.4 遍历

在实验中根据图像长和宽和的奇偶性对图像进行顺逆时针遍历，设l为图像的长，h为图像的宽。

若l+h为奇（偶）数，则以顺（逆）时针遍历的方式进行DNA编码与解码的加密。

4 基于ACGAN的无载体信息隐藏

本文提出的无载体信息隐藏的流程图如图3所示，在ACGAN中，它的生成装置可以通过输入不同类别标签以获取特定图像，判别装置则可以从特定图像中提取输入的类别标签，完成了秘密信息的提取，创建了一种无载体信息隐藏方法。

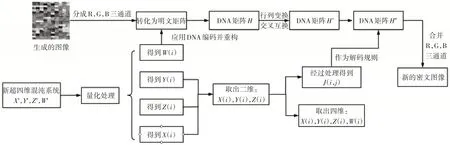
图3 无载体信息隐藏流程图

4.1 ACGAN生成图像排序组合

1）信息隐藏可以使用ACGAN 类别标签的特性。发送方首先对二进制秘密信息S按照长度L进行了索引，得到S={s1,s2,s3…,sn} ，n 为秘密信息段的数目。

2）分别将s1,s2,s3…sn作为生成器的标签，与噪声z 一同作为输入生成图片，将所有的生成图片根据公共通道中的密钥按特定顺序组成一幅组合图像。

3）通过对组合图像进行加密置乱操作，以获得加密组合图像，并交由安全信道向接收方传输。

根据本文对秘密图像的加密方法使用的混沌系统和DNA 编码，在文献［6］的加密算法基础上加以改进，具体流程如图4所示。

图4 ACGAN训练流程图

4.2 多维多重混沌系统序列生成

通过发送方选择的Logistic 映射函数初始值对其进行量化处理得到长度为M×4N且取值为1～9的混沌序列L(i)，如式（7）所示：

根据L(i)决定两个混沌系统的序列长度，通过混沌序列加强两个混沌系统的交替切换，可有效解决混沌收敛问题并增加混沌序列的复杂性。图5给出了示意图。

图5 混沌序列生成示意图

其中x1表示式（2）的混沌系统第一维度X，x2表示式（3）的混沌系统。

4.3 组合图像加密

将新图像分解成R，G，B 三通道，进行以下操作：

1）通过发送方选择的初始四维，分别对两个新超混沌系统的第四维W 量化处理，得到一个M×4N 的混沌序列W（i），如式（8）所示，并使得取值为1～8。

利用混沌序列W（i）将明文转成的大小为M ×8N 的二进制矩阵，以W（i）中的值为DNA 编码所使用的规则对与其对应的两比特位进行DNA 编码，最后重构成大小为M×4N的DNA矩阵H。

2）借助于新超四维混沌系统产生的第一维x和第二维y 形成两个长度分别为M 和4N 的向量，利用式（9）对其进行量化处理：

使得DNA矩阵H的第i行与第X（i）行互换，第j行与第Y（j）列进行互换，得到矩阵H'。

3）将新超四维混沌系统的四维分别作为交叉点对矩阵H'进行交叉置乱，各交叉点如式（10）所示：

其中，Rt（i）和Re（i）分别为矩阵H'中第i 行进行行交叉的头交叉点和尾交叉点，而Ct（j）和Ce（j）分别为第j列进行列交叉的头交叉点和尾交叉点。

交叉置乱实质是对矩阵H'选定两行（列）的头交叉点Rt（i）（Ct（j））与尾交叉点Re（i）（Ce（j））中的部分碱基置换。

本文是对矩阵H' 的第i 行（j 列）与第M-i 行（4N-j 列）分别进行一次交叉置乱，然后再对第i 行（j列）与第M/2+i行（2N-j列）进行交叉置乱，按照各交叉点进行交叉置乱后得到矩阵H''。

4）对H''利用J(i,j)解码规则进行解码获得R通道的加密图像R'。J(o)的解码规则如式（11）所示：

其中i 和j 为H''中碱基的坐标，利用混沌系统的前三维生成J(i,j)作为该碱基的解码规则，经试验证明，该方法可有效降低相邻像素之间的相关性。

5）使用上述方法对R，G，B三个通道进行相同操作得到R'，G'，B'，最后将三通道合并得到经过加密置乱后的生成图像组合排序的新图像。

当发送方使用不同的混沌系统初始值与解码规则时，可以得到不同视觉效果的加密组合图像。接收方需从安全通道获得密钥，才可以正确解密。

4.4 信息提取与恢复

发送方需将训练好的ACGAN判别器与加密组合图像和使用的密钥发送给接收方，具体步骤如下：

1）接收方获取加密组合图像和ACGAN 判别器后，根据接收到的密钥得到混沌系统初值和解密规则进行解密操作，得到由生成图片组成的图像，再根据公共密钥依次提取出有类别和顺序的生成图像集合。

2）使用ACGAN 判别器对生成图像集合进行判别，获得顺序的类别集合NC，将其按照顺序排列即为二进制秘密信息S中所对应的秘密信息片段。

3）由密钥Q 获得混沌系统的四维，对二进制秘密信息S 根据加密的逆过程进行解密即可还原出原始图像。

5 实验

本文实验中ACGAN 的训练在Windows 11 操作系统上完成，使用Tensorflow1.14.0 深度学习平台，计算显卡设备为NVIDIA RTX 3060。样本数据集是纹理图像数据集，如图6 所示，均为96×96 像素的纹理图片，输出图像为48×48 像素。网络的学习率为0.0002，训练epoch为4000，步长为100。

图6 相关数据集

5.1 实验结果

本文的实验首先对秘密图像进行了基于新超4 维混沌系统的加密，图7（a）为实验中采用的原始图像，为保证实验表现的准确与效率，本文实验所选择的图像大小为512×512，图7（b）则是其加密后的图像。

图7（c）为分段处理的秘密信息与噪声一同输入ACGAN 获得生成图像集，对其按照公共密钥进行排序组合获得新图像如图7（d）所示。

图7 加密过程生成图像

最后对组合图像进行加密置乱操作，本实验Logistic初值为3，两个四维混沌系统使用的初值均为x=5，y=6，z=4，w=7，解密规则使用的是规则3，最终得到经过加密置乱后的组合图像如图7（e）所示。经提取秘密信息并解密还原得到的图像为图7（f）。

5.2 实验结果分析

本文算法与一般使用GAN 的信息隐藏算法不同，秘密信息隐藏在类别标签中，对组合生成图像也进行了加密置乱，所以只需保证判别器的准确率稳定即可。

5.2.1 隐藏容量分析

本文的隐藏方法是使用已经训练好的数据集作为标签载体，此时所使用的数据集图像数量直接决定了隐藏容量。

在式（12）中，Ls为秘密信息总长度，Lc为每个生成图像所能携带的秘密信息的长度，Tw和Th表示生成图像的宽度和高度，Gw和Gh表示生成图像的宽度和高度。设生成图像长宽为1080×1080，不同数据集所能携带的秘密信息长度如表2所示。

表2 不同数据集所能携带的秘密信息长度

此时的隐藏容量与标签的长度和与秘密信息的相关度成正比，发送者可在不同情况下选择最适合的标签进行训练。

5.2.2 图像直方图

灰度直方图是通过计算图像中灰度值的分布，把各个灰度值的数量表示出来。本文对比了组合图像和加密组合图像R 通道的直方图，如图8 所示。

图8 R通道灰度直方图

从图中可以看出组合图像是多种生成图像的组合，在其R通道的直方图中显示出灰度值分布不均匀，而在加密置乱后有效均衡了灰度值的分布。

5.2.3 相邻像素相关性

相邻像素相关性反映了图像相邻位置像素值的关联情况。我们对彩色的尺寸为512×512×3的Lena 图像进行了本文组合图像的加密置乱，并根据该像素位置分析了水平、垂直、对角像素三个部分，在各方向上任意选取了7000 对相邻像素点利用式（13）计算相关系数进行分析。

式中，xi和yi分别为相邻像素的灰度值，N 代表所选取的像素对的数量，本文中N为7000。相关系数计算结果如表3～5 所示。可以看出，所有明文图像的相邻像素相关系数都较大，而在其加密置乱图像中，相关系数分析结果较为接近零。此外，对比改进前的文献［6］中的加密算法以及文献［7］和文献［8］提出的方法，本文的方法能够更好地消除相邻的像素的相关性，且更有助于对组合图像数据特征的掩盖。

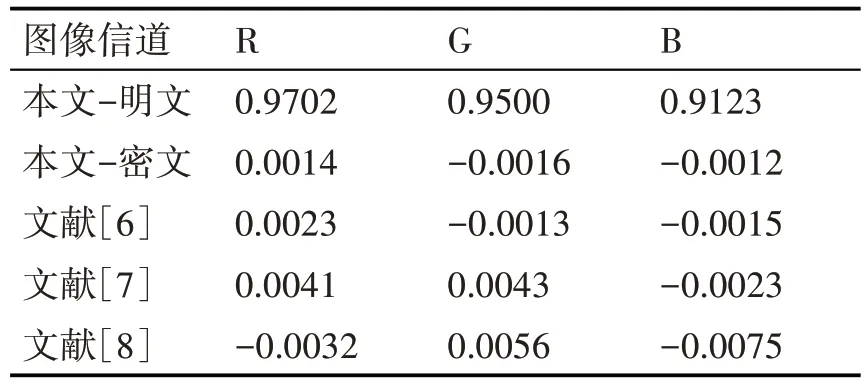
表3 水平方向相关系数值

表4 垂直方向相关系数值

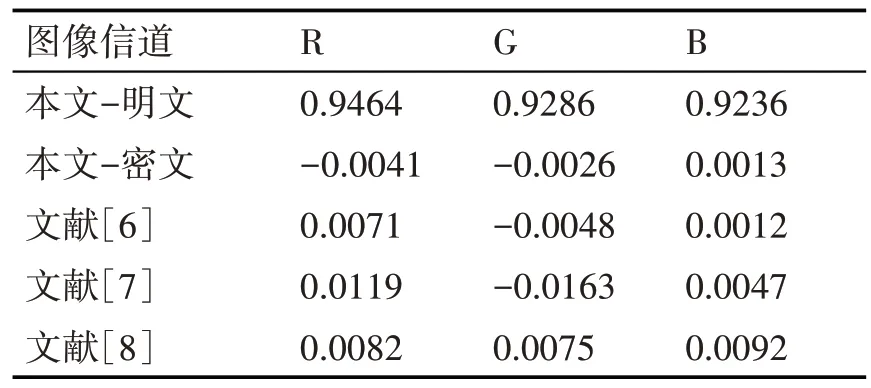
表5 对角方向相关系数值

5.2.4 提取准确率

本文在提取出的生成图像上做了类别提取准确测试。在不同训练次数情况下使用发送给的判别器对生成图像进行判别获得类别标签，在训练前期提取标签的错误率较高。当训练次数达到3000时，提取错误率降低至0.03%，加入冗余码还可进一步降低，可保证提取出的秘密信息的准确性。

6 结语

本文提出了一种基于ACGAN和多重多维混沌系统的无载体信息隐藏方法，将新四维超混沌系统、DNA 编码、ACGAN 与无载体信息隐藏有机结合。既保证了图像传递的安全性与隐蔽性，又避免了修改原始图像。与其他信息隐藏算法相比，本文提出的算法安全性高、容量大、准确性高。然而，本文所采用的数据集相对简单，最终生成的图像质量仍可提升。通过添加冗余码的方法可进一步降低提取的错误率。未来的研究工作将上述方面进行优化，并选用更优数据集来改善图像质量并提高算法的隐蔽性与安全性。