俯冲带板间地震竖向加速度谱的阻尼修正系数模型

张峻华,黄 斌

(山东建筑大学 土木工程学院,山东 济南 250000)

0 引言

我国台湾省和南海东部地区的地质构造复杂和地震频发,位于太平洋板块与亚欧板块共同作用的俯冲带区域[1]。随着我国对南海区域的不断开发,近海交通建设工程与海洋工程日益增多,俯冲带地区抗震研究越来越重要,但由于我国地震观测网络的建设起步较晚,可供研究使用的俯冲带地震记录较少,针对俯冲带的地震特性研究将是海洋工程开发中需面临的重要课题。

目前对俯冲带区域地震动特性的研究多基于5%阻尼比的结果,例如ZHAO等[2]。但在海洋工程中广泛使用的钢结构建筑的阻尼比要低于5%;空间网架结构、长悬臂结构和大跨度组合楼板的阻尼比同样低于5%[3-5];安装抗震耗能构件的建筑物阻尼比要高于5%,由此可见5%阻尼比的设计谱无法满足复杂多样的设计需求。利用阻尼修正系数(Damping Modification Factors,DMF)的方法来克服5%阻尼比设计谱的局限,是在现阶段抗震设计中常用的方法。阻尼修正系数是地震记录在某一阻尼比下的反应谱谱值与其在5%阻尼比下反应谱谱值的比值,加速度谱阻尼修正系数Ba定义如式(1)所示：

(1)

式中：ζ为阻尼比,T为谱周期(s),Sa(T,ζ)和Sa(T,0.05)分别表示谱周期为T、阻尼比为ζ和5%时的加速度反应谱值。

早期研究者们发现反应谱的形状和谱周期与阻尼比有较为紧密的联系,NEWMARK等[6]在1982年建立了最早的阻尼修正系数模型,该模型只包含阻尼比一个参数,对绝对加速度、相对加速度和相对位移反应谱分别给出了阻尼修正系数,并被应用于当时的美国抗震设计规范。随着地震研究的逐步深入,更多影响DMF的因素被不断发掘。LIN等[7]认为谱周期和阻尼修正系数值有较大的关联;蒋建等[8]使用我国观测的地震数据研究各阻尼比下不同场地类别的阻尼修正系数,认为阻尼修正系数与场地相关;王国弢等[9]利用美国PEER地震数据,采用非线性回归分析,建立了位移谱阻尼修正系数模型,该模型考虑了地震持时与震级两类影响因素;李恒等[10]认为近场范围内不同场地类别的阻尼修正系数差异显著,并且随着距离增大这种差异逐渐缩小;HAO等[11]认为研究震级和震源距离等因素对阻尼修正系数的影响时,需要使用控制变量法进行分组研究,避免各种因素之间的相互影响产生误差。

过去关于地震动衰减关系与阻尼修正系数的研究多以水平向为主,针对竖向地震动采用反应谱比的方法,将其取值为水平向地震动的2/3。但在近几十年的地震中多次出现竖向地震加速度峰值高于水平地震加速度峰值的记录[12],需直接建立竖向地震动阻尼修正系数模型,以保证大跨结构和长悬臂结构等竖向抗震能力薄弱的结构具备充分抵御竖向地震作用的能力。

此外,俯冲带区域地质构造复杂,不同类型地震动衰减特性有较大差异。按传统方式,俯冲带地震可划分为板间地震(Subduction Interface)与板内地震(Subduction Slab),这种划分方式主要考虑了板块的俯冲角度,震源深度以及岩石圈厚度等影响因素。针对俯冲带地震的研究最早兴起于上世纪80年代,主要的研究区域集中在美国西海岸地区与日本地区。关于俯冲带地震衰减关系的研究,早在2000年SI等[13]通过分析日本地区的地震记录发现板间地震、板内地震和浅壳地震(Shallow Crustal)三者之间的地震特性有明显差别。此后ATKINSON等[14]综合分析了全球矩震级处于5～8.3级的俯冲带地震记录,认为在全球任何地区,不同类型的俯冲带地震其衰减关系都有明显的差异性;胡进军等[15]利用数值计算结果和实际的地震记录,分析后得出：板内地震,浅壳地震,板间地震的衰减依次减慢。因此分类研究研究俯冲带地震是极为必要的。本文使用ZHAO等[16]提出的更为细致的俯冲带地震分类方法,该方法通过对比日本气象厅、美国国家地震信息中心与国际地震中心提供的震源坐标,并借助美国地质调查局的Slab1.0俯冲带几何模型,根据地震动衰减关系的拟合优度与震源相对于俯冲板块的位置,将俯冲带地震进一步划分为板间地震、板内地震、浅壳地震和上地幔地震(Upper Mantle)。

按照以上四种地震类型,分水平向地震与竖向地震,研究团队建立了一系列相对应的位移谱DMF模型和加速度谱DMF模型,如：张衡等[17]、杨新格[18]、苏开潍等[19]、姜明秀等[20]、张潇男等[21]、刘名吉等[22]、张洪博等[23]、姜妍旭等[24]、王本三等[25]、陈心锋等[26]和靳羽阳[27]。本文的研究是研究团队一系列研究成果的最后一部分,通过使用K-NET与KiK-net台站记录的俯冲带板间地震数据,依据ZHAO等[28]分四类场地建立包含阻尼比与谱周期两个参数的俯冲带板间地震竖向加速度谱阻尼修正系数模型,并利用残差标准差分析模型误差的来源。该研究所得到的模型是为修正无指定震级及震源距离参数的设计反应谱,因此模型不考虑这些参数导致的残差偏移。最终结果可为我国俯冲带地区(台湾省和南海地区)的抗震设计提供参考。

1 地震数据选取与场地划分

1.1 数据筛选

根据ZHAO等[16]提出的分类方式,俯冲带板间地震被定义为：震源深度在俯冲板块高度的上下5 km以内,震源深度小于50 km,震源机制为逆断层,其中破裂面的倾角应在俯冲板块倾角的上下15°范围内。本文选用的俯冲带地震记录均在此范围内。

为获取有效可靠的地震数据,本文对地震记录的原始数据进行以下处理：

(a)剔除矩震级MW<5.0的地震记录、缺少竖向分量的地震记录、场地信息不完整的地震记录和震源信息不完整的地震记录。

(b)检查记录的加速度时程,去除P波或S波不完整的或波形有明显错误的地震记录。

(c)仪器响应校正与基线校正。

(d)滤波：考虑到采用频率的影响及不同频率地震动对工程结构的影响,对于采样频率为50 Hz和100 Hz的记录,分别选用24.5 Hz和33.3 Hz作为低通截止频率。高通截止频率则根据位移时程,通过人工判别确定,最终所确定的高通截止频率位于0.05 Hz与2.0 Hz之间,未选用高通截止频率大于2.0 Hz的地震动。

通过以上处理流程,可消除地震记录中影响地震信息的噪声。同时,利用距离与震级关联的方法选取震源距300 km的范围内的地震记录。最终筛选出来自日本K-NET与KiK-net台网的76个俯冲带板间地震的3 552条地震动记录用于建立DMF模型。筛选的地震数据在各个矩震级下的分布情况如图1所示。

图1 强震数据的分布Fig. 1 Distribution of strong-motion date

1.2 场地类别划分

依据ZHAO等[28]的场地分类方法,按照场地周期Ts将场地类别(Site Class,简称SC)划分为SC Ⅰ～Ⅳ四类,Ts的定义如式(2)-式(5)所示：

(2)

(3)

(4)

(5)

式中：H为地表至基岩上表面的土层厚度(m);Vsite为H深度范围内的土层传播时间加权剪切波速(m/s);hi为第i层土层厚度(m);vi为第i层土层厚度(m);TVS30为伪场地周期。表1所示为本文使用的地震数据按照场地类别分组。

表1 不同场地的场地周期划分与对应的地震记录数量Table 1 Division of site periods for different sites and the number of records to each site classes

2 建立加速度谱阻尼修正系数模型

2.1 不同场地类型下的DMF分布

在阻尼比1%～30%的范围内选取1%～10%和15%～30%共计14个常用的阻尼比,在谱周期0.01 s～5.00 s的范围内选取0.01～0.10 s、0.12～0.20 s、0.25～0.50 s、0.60～1.00 s、1.25和1.50～5.00 s共计36个谱周期来计算阻尼修正系数几何均值用作本文的计算数据。

利用半对数坐标,图2(a)-图2(d)分布给出了阻尼比为1%、4%、10%和25%时,四类场地的阻尼修正系数几何均值随周期变化的趋势。可见：(a)同一阻尼比和不同场地类别时,阻尼修正系数几何均值的分布曲线随谱周期变化趋势相同,但仍有小范围内的差异,在谱周期0.03 s 0.32 s时,SC Ⅳ曲线走向较其它三类场地分散。(b)在T<0.03 s时,四类场地的阻尼修正系数几何均值在各阻尼比下均趋近于1。(c)在1%≤ζ<5%时,四类场地的阻尼修正系数几何均值随谱周期先增后减;在5%<ζ≤30%时,四类场地的阻尼修正系数几何均值随谱周期先减后增。

图2 SC Ⅰ～SC Ⅳ场地几何均值随谱周期的分布图Fig. 2 Distribution of geometric mean values with spectral period for four site class

同时本文使用t检验对四类场地的阻尼修正系数进行显著性检验,分析场地类别与阻尼修正系数之间的关联性。统计值Z如式(6)所示：

(6)

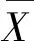
本文选取1%、4%、20%和30%阻尼比的四类场地阻尼修正系数几何均值,检验每两类场地阻尼修正系数之间是否具有显著差异性,检验结果如图3所示。①图3(a)为SC Ⅰ与SC Ⅱ场地阻尼修正系数关联性检验结果,在谱周期<0.1 s的范围内,各阻尼比下的|Z|均大于1.96,两类场地阻尼修正系数差异显著,在谱周期>0.1 s时,低阻尼比下的两类场地阻尼修正系数差异显著。②图3(b)与图3(c)为SC Ⅰ与SC Ⅲ、SC Ⅳ场地阻尼修正系数差异性检验结果,在大多数谱周期内,不同阻尼比下,两类场地阻尼修正系数均有明显差异。③图3(d)为SC Ⅱ与SC Ⅲ场地阻尼修正系数差异性检验结果,在部分长周期范围内|Z|≥1.96,两场地阻尼修正系数有明显差异,且阻尼比越小,差异越明显。④图3(e)与图3(f)为SC Ⅳ与SC Ⅱ、SC Ⅲ场地阻尼修正系数差异性检验结果,在长周期范围内,两类场地阻尼修正系数之间有明显差异。

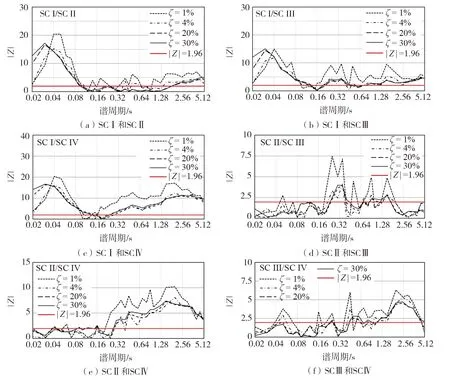
图3 四类场地显著性检验统计值Fig. 3 |Z| values for four SC Ⅰ～SC Ⅳ sites

综合以上分析,在大多数谱周期范围内,统计值|Z|≥1.96,表明不同场地的阻尼修正系数之间有明显差异,场地类别与阻尼修正系数之间有明显关联。为保证模型建立方法的科学性,需分场地类别建立阻尼修正系数模型。

2.2 建立DMF模型

分场地建立DMF模型过程中,对四类场地分别取谱周期为0.02、0.2和5.0 s的阻尼修正系数几何均值的自然对数ln(Ba),绘制ln(Ba)关于阻尼比自然对数值ln(ζ)的分布图,如图4所示,可以发现利用阻尼比自然对数的三次函数曲线,即可对各个谱周期下对应的散点分布有良好的拟合效果。若使用二次函数曲线拟合,则拟合效果较差,不能准确反映两者之间的趋势走向;若使用四次函数拟合,会致使拟合参数较多,拟合方程复杂。最终考虑阻尼比与谱周期两类参数,选取阻尼比自然对数的三次多项式方程建立DMF模型,如式(7)所示：

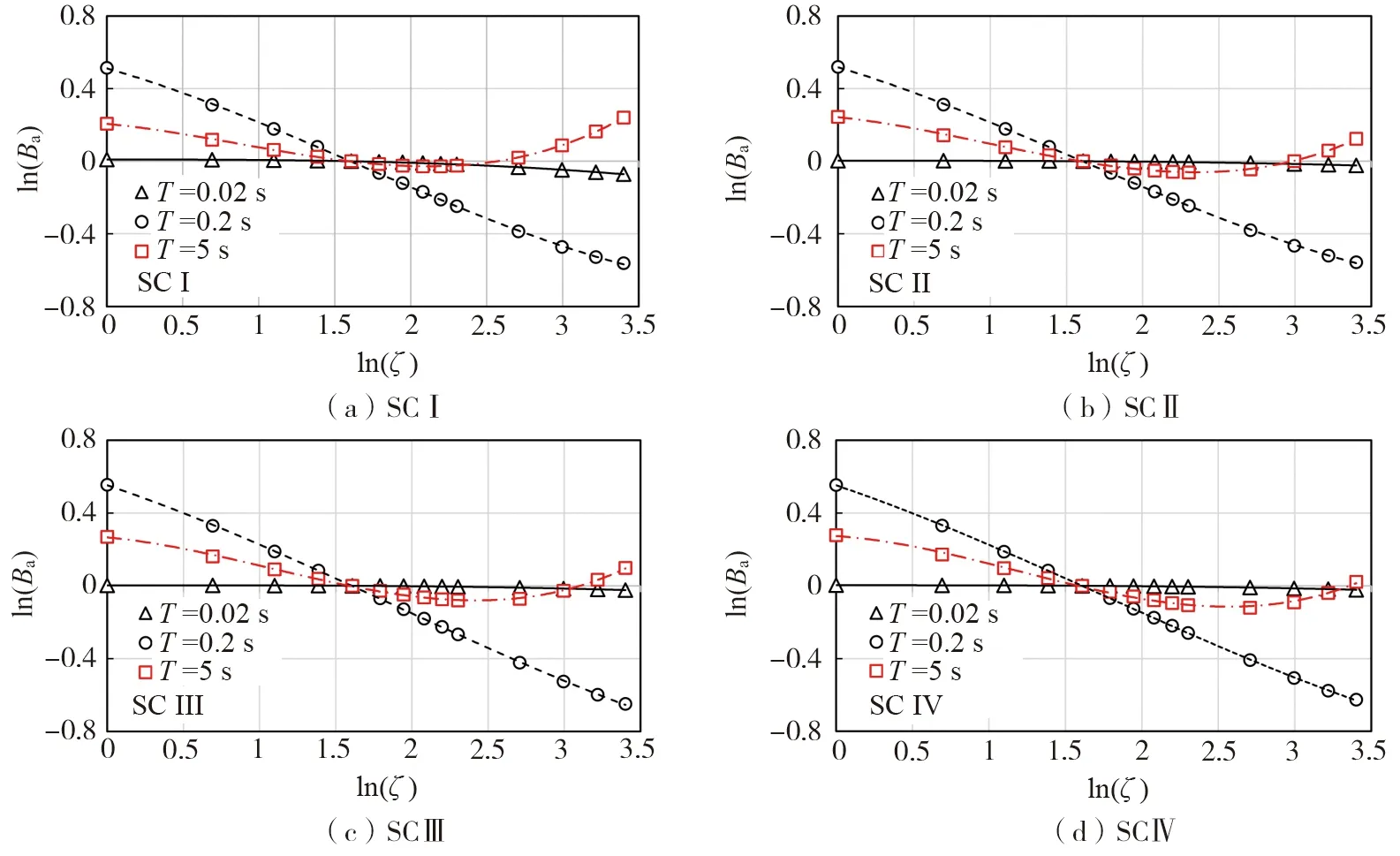
图4 SC Ⅰ～SC Ⅳ场地阻尼修正系数几何均值的自然对数值随阻尼比自然对数值的变化趋势Fig. 4 Trend of the natural logarithm of the geometrical mean of damping modification factors with the natural logarithm of the damping ratio for SC Ⅰ～SC Ⅳ sites

(7)

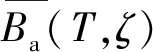
在对DMF模型曲线进行平滑时：第一步,从a、b和c中任选一个系数,使用谱周期自然对数的四次函数式进行平滑;第二步,将已平滑的系数,带入DMF模型方程可得另外两个系数的新值,从这两个系数中再任选其一,重复第一步,将平滑后得到的系数固定,并代入回归方程得到最后一项系数的新值;第三步,对最后一项系数进行平滑,平滑过程与前两步相同。在第一次完成上述过程后,得出的曲线可能尚不具备良好的拟合效果,因此需要多次重复上述过程,并对系数进行适当调整。

确保模型拟合度为前提,利用四次函数把谱周期大于0.06 s时的ak、bk、ck与谱周期对数进行线性回归得出另一个系数uk,i,j,以减少模型计算所需的数据量,由此式(7)可写为式(8)所示的形式：

(8)

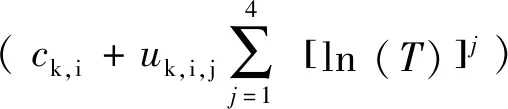
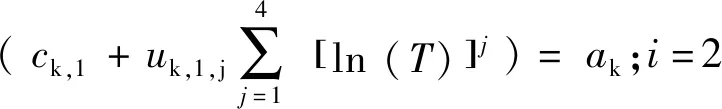
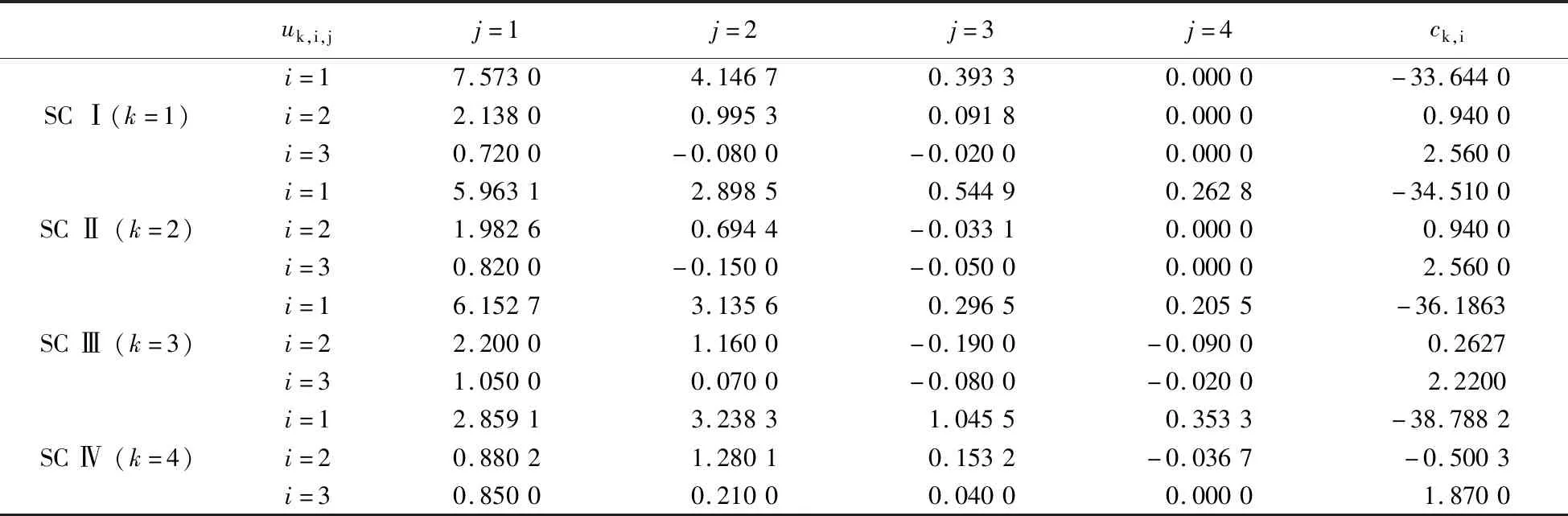
表2 系数uk,i,j(×100)Table 2 Coefficient uk,i,j(×100)

谱周期小于0.06 s时的ak、bk和ck的由表3给出。

表3 DMF模型回归系数Table 3 Model parameters for the DMF models

图5所示为7条不同阻尼比下的DMF模型在四类场地中的拟合曲线与实际的阻尼修正系数的几何均值的对比。可见：在各个谱周期内计算曲线与实际数据都有良好的拟合效果,计算曲线符合在周期0.01～0.3 s范围内趋近于1,以及在不同场地中,阻尼比在1%～5%范围内先增后减,5%～30%范围内先减后增的规律。

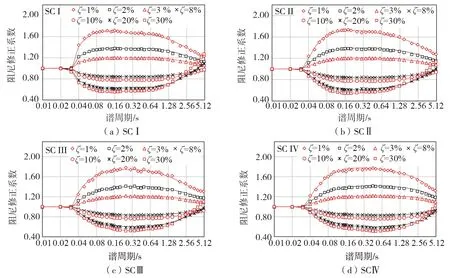
图5 四类场地DMF模型拟合曲线与Ba几何均值的对比Fig. 5 DMF curves and the geometrical mean of Ba for SC Ⅰ～SC Ⅳ sites

3 DMF模型残差与标准差分析

分析前文中DMF计算曲线的拟合优度并分析模型误差来源,需对残差标准差进行分析。采用随机效应模型[29],将总残差分为事件内残差与事件间残差,用于分析DMF模型与每条地震记录之间的拟合优度。其中总残差表达式如式(9)所示：

(9)

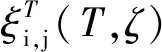
将总残差分为事件间残差与事件内残差,如式(10)所示：

(10)

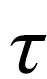
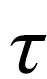
(11)

现阶段,国内外研究成果均表明震源效应与路径效应都是对DMF模型有重要影响的参数。但本文建立的模型适用于调整无震源效应和路径效应的5%阻尼比下的加速度设计反应谱,并未考虑震源效应与路径效应对DMF模型的影响。

选取谱周期为0.16 s和阻尼比为30%,绘制如图6所示的事件间残差与震级、震源深度的分布图。图6(a)所示的事件间残差随震级分布的趋势线有明显倾斜,表明两者之间具有较强的相关性;图6(b)所示的事件间残差随震源深度分布的趋势线有明显倾斜,表明两者之间具有较强的相关性。以上现象可通过引入震源效应这一因素提高模型拟合度,降低模型误差。

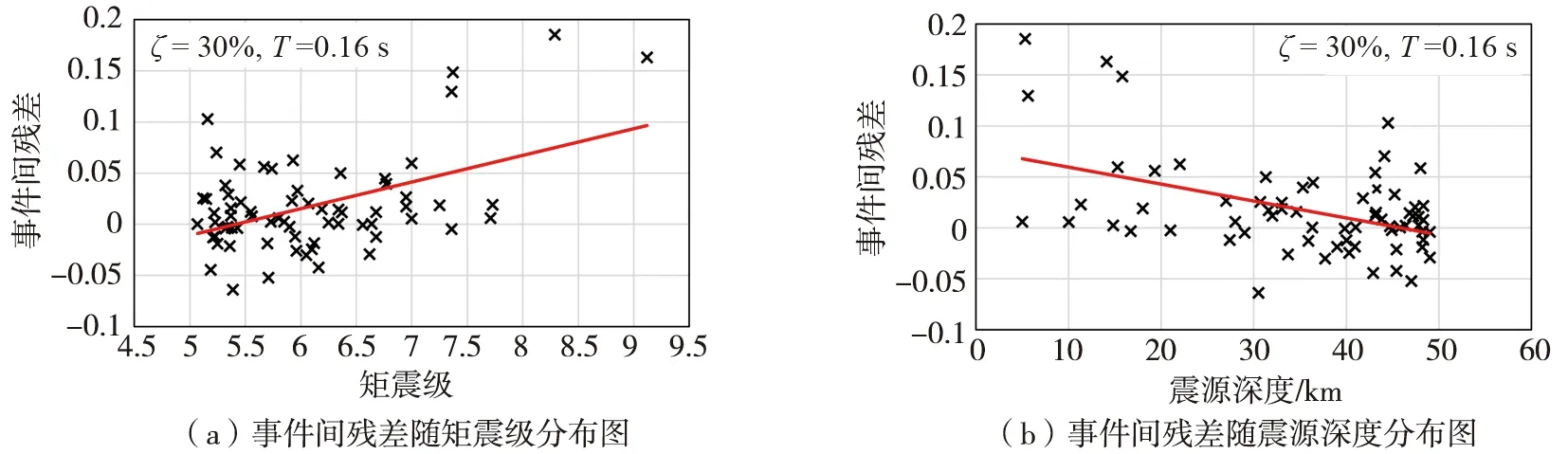
图6 事件间残差分布图Fig. 6 Distribution of residuals between events

在谱周期为0.16 s、阻尼比为30%的情况下,绘制事件内残差与震级、震源距的绘制,如图7所示。其中：图7(a)显示事件内残差与震级分布图的趋势线趋近于水平,表明两者之间相关性弱;图7(b)显示事件内残差与震源距分布图的趋势线明显倾斜,表明两者之间具有较强的相关性。因此,可通过引入路径效应与场地效应项提高模型拟合度,降低模型误差。

图7 事件内残差分布图Fig. 7 Distribution of residuals within events

事件内残差标准差、事件间残差标准差和总残差标准差分别由表4-表6给出。残差标准差值越小,说明模型计算值越接近实际值,模型的拟合度越好。根据表中数据可见：当阻尼比处于1%～5%范围内,残差标准差均随阻尼比增大呈递减趋势;当阻尼比处于5%～30%范围内,残差标准差随阻尼比增大呈递增趋势;总残差标准差在谱周期5 s和阻尼比30%时数值最大为0.734,表明拟合效果良好。

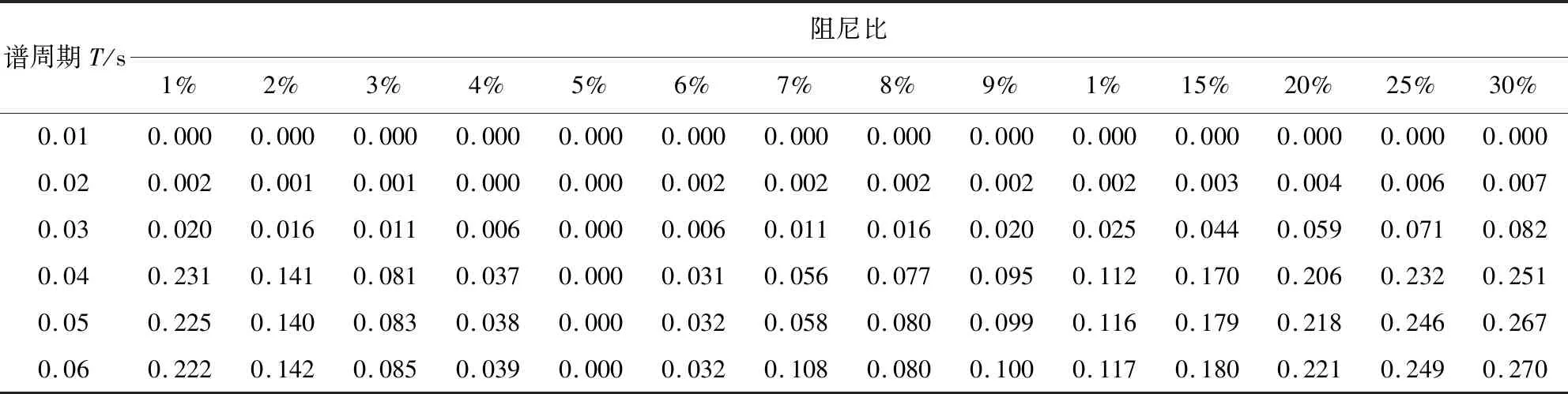
表4 事件内残差标准差Table 4 Within-event standard deviations

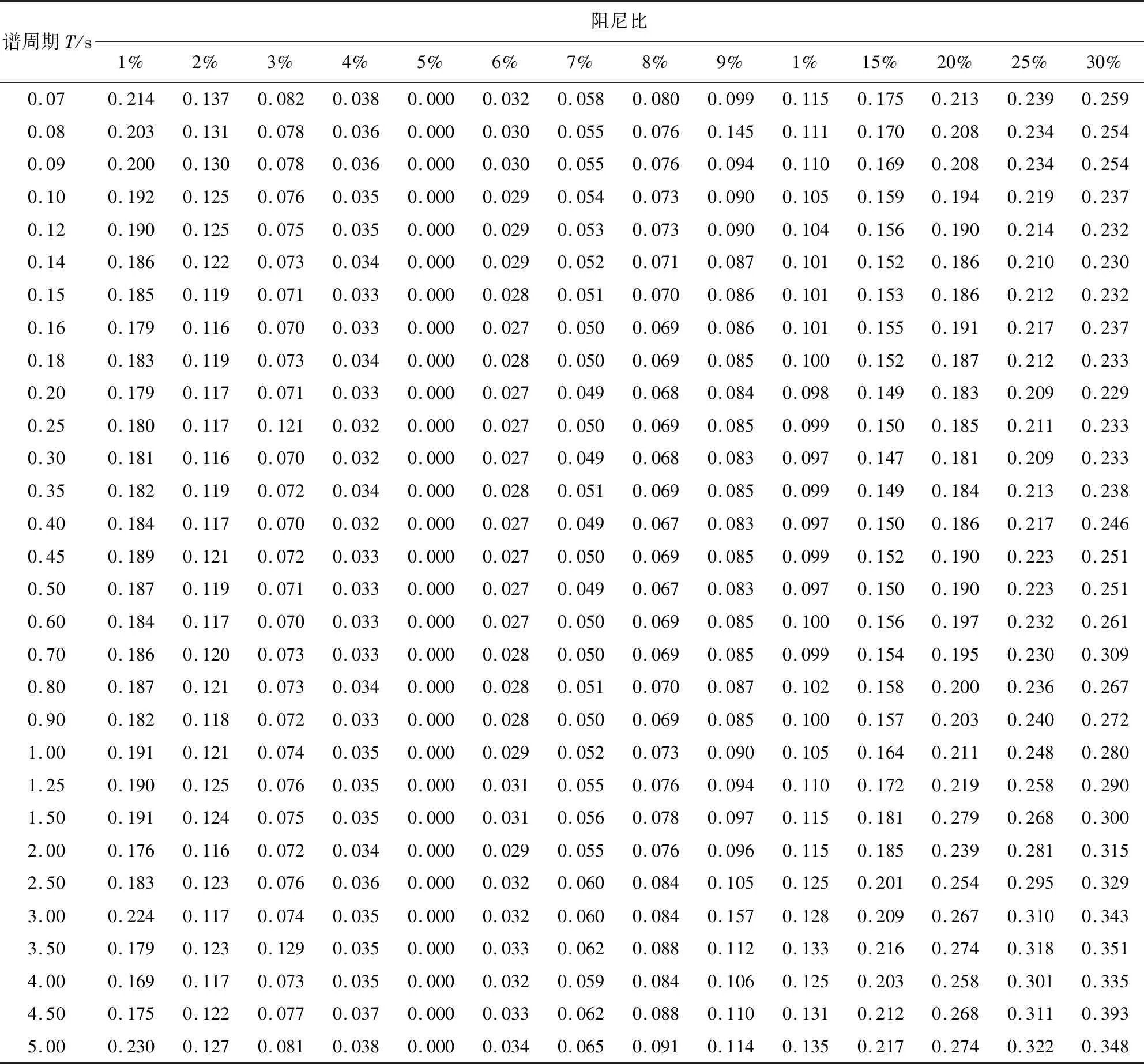
续表

表5 事件间残差标准差Table 5 Between-event standard deviations

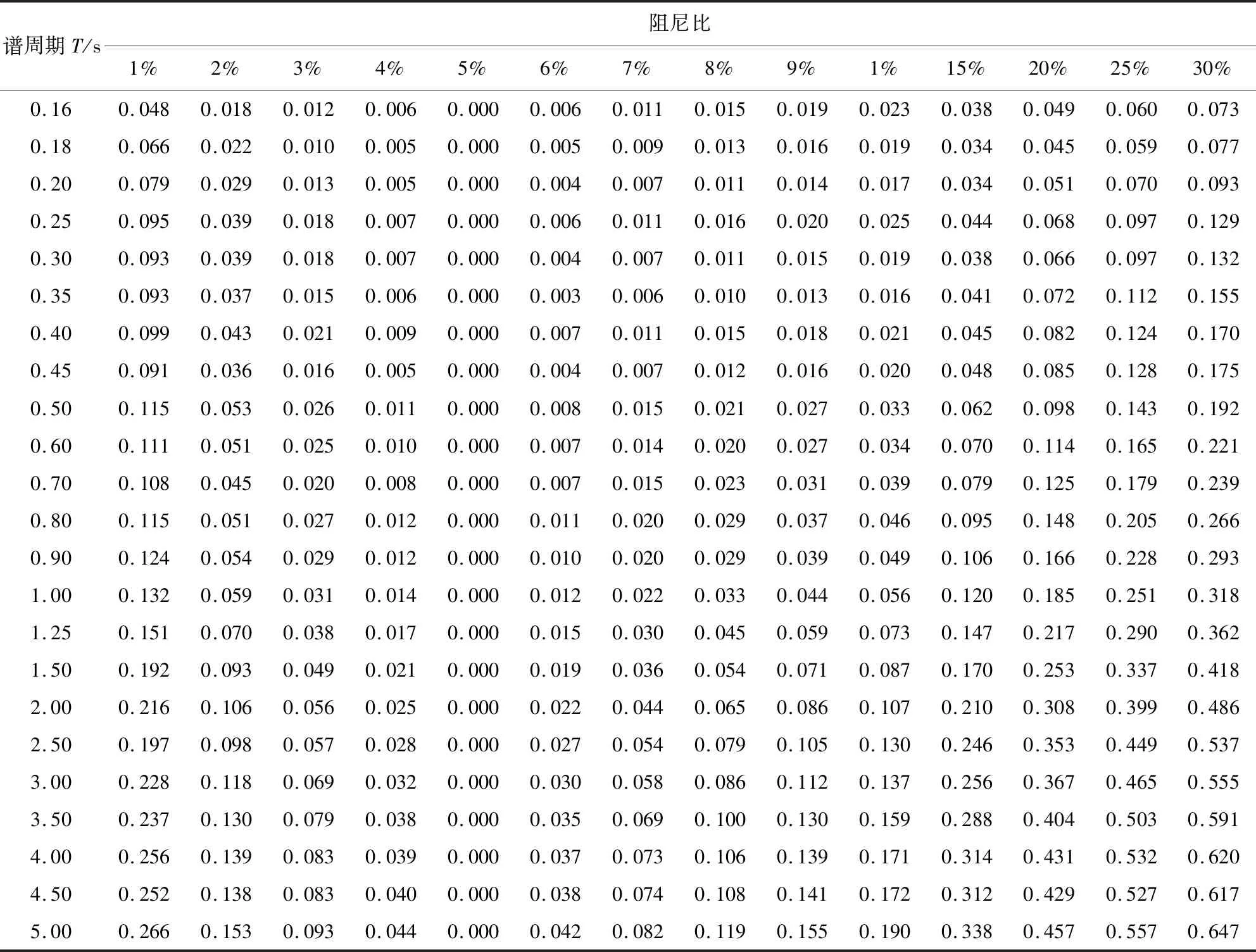
续表

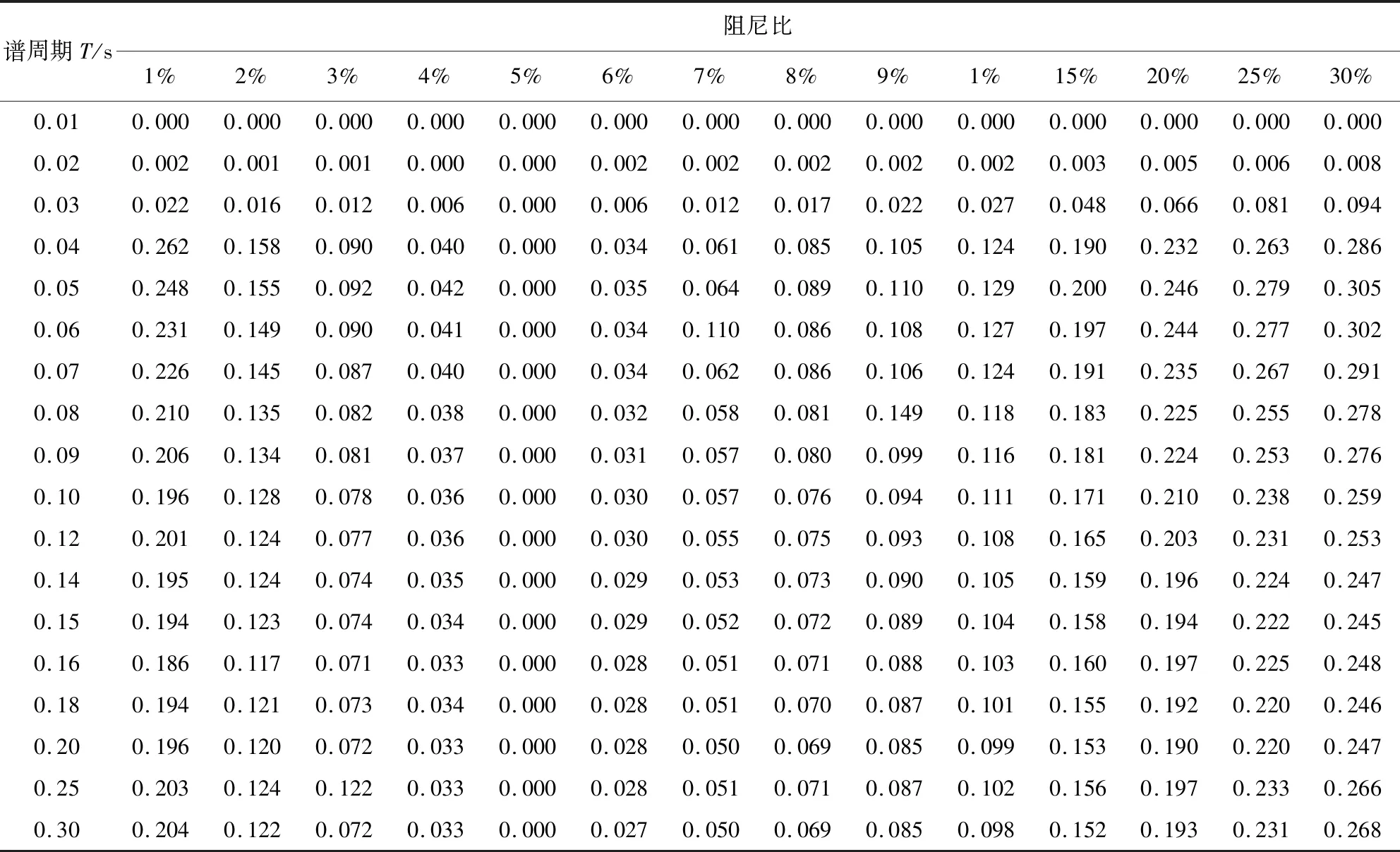
表6 总残差标准差Table 6 Total standard deviations

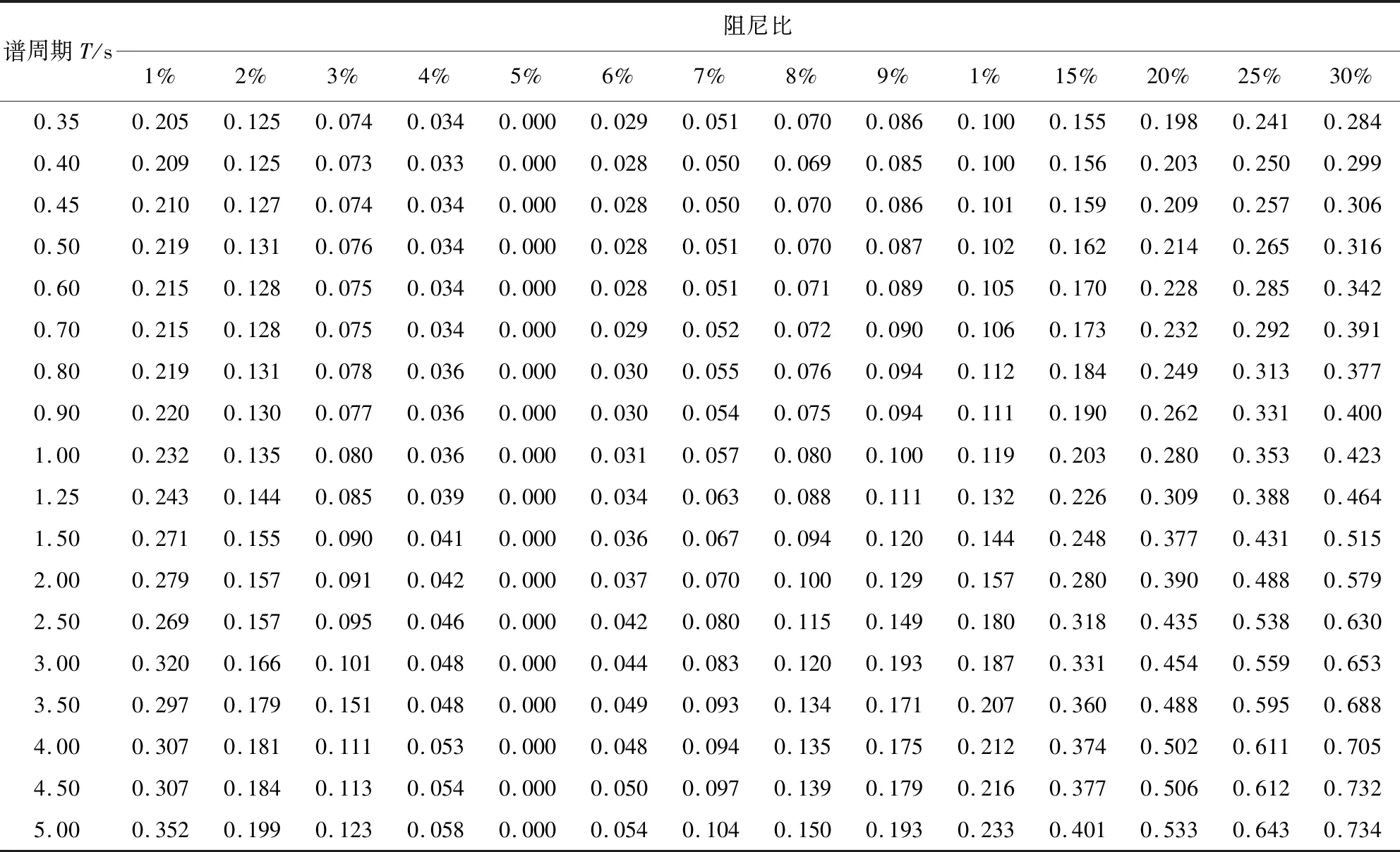
续表

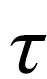
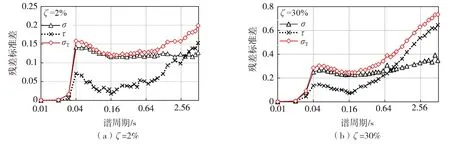
图8 残差标准差分布图Fig. 8 Distribution of standard deviations (σT,,and σ)

以上现象表明：在短周期内,路径效应与场地效应的引起的误差大于震源效应引起的误差;长周期时,震源效应的误差大于路径效应与场地效应引起的误差,且随着阻尼比增大,路径效应与场地效应引起的误差呈增大趋势。

事件内残差由场地内残差与场地间残差组成,其标准差σ与场地内和场地间残差标准差的关系可通过式(12)表示：

(12)

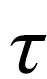
图9为四类场地总标准差在不同阻尼比下的分布图,其变化规律为：阻尼比小于5%,总标准差随阻尼比增大而减小;阻尼比大于5%,总标准差随阻尼比增大而增大。此外,SCⅠ场地在谱周期小于0.06 s的范围内的标准差通常要高于其它三类场地。

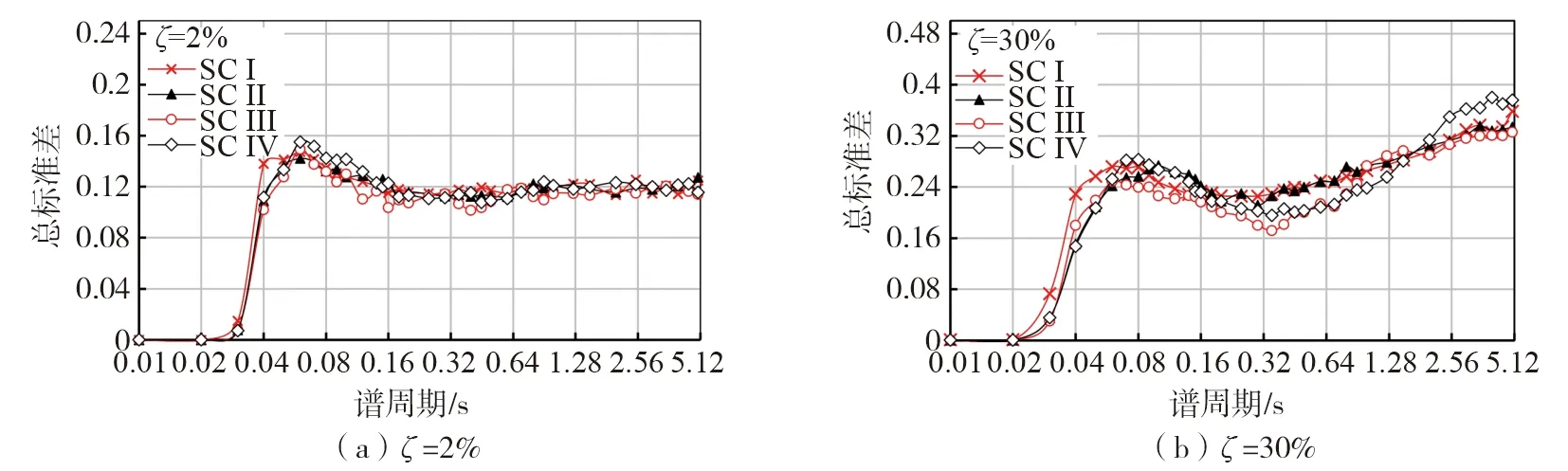
图9 四类场地总标准差分布图Fig. 9 Distribution of the total standard deviation of the four site classes

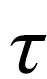
图10 SCⅠ场地模型总标准差分布图Fig. 10 Distribution of total standard deviations for SCⅠ

4 对比现有DMF模型

4.1 对比XIANG和HUANG(2019)模型

XIANG和HUANG利用日本地震数据库中的3 198条竖向地震动数据[30],以5%竖向反应谱为基准,在谱周期0.03～10 s,阻尼比0.5%～40% 的范围内建立了未考虑场地条件与地震类型的竖向阻尼修正系数模型(后文简称“XH2019模型”),并计算了竖向伪加速度谱与竖向加速度谱的阻尼修正系数。其中竖向加速度谱阻尼修正系数模型如式(13)和式(14)所示：

DMF=a5(lgT)2+b5lgT+c5

(13)

DMF=a6+b6cos(f6lgT)+c6sin(f6lgT)+d6cos(2f6lgT)+e6sin(2f6lgT)

(14)

式(13)适用于谱周期0.03 s≤T≤0.12 s;式(14)适用于谱周期0.12 s≤T≤10 s。

XH2019模型按照谱周期划分为两段,针对每个阻尼比设置了9个回归参数,并将其与本文模型进行相互比对,以验证本文DMF模型建立的合理性。DMF值在两段周期交界点处不平滑,容易造成计算反应谱在交界点附近的周期出现峰谷值。

以SC Ⅱ场地与SC Ⅳ场地为例,图11为本文建立的DMF模型的计算值与XH2019模型的计算值在阻尼比为1%、3%、15%和30%情况下的对比,从图中可见：(a)不同场地条件,不同阻尼比下,本文所建DMF模型与XH2019的计算值随谱周期变化趋势一致,表明本文所建DMF模型正确合理。(b)阻尼比为1%与3%,在谱周期<0.16 s的范围内,本文所建模型的计算值小于XH2019模型的计算值,且谱周期越短差异越明显;在谱周期>0.16 s的范围内,本文所建模型的计算值大于XH2019模型的计算值,且谱周期越大差异越大。(c)阻尼比为15%与30%时,在谱周期<0.16 s的范围内,本文所建模型的计算值与XH2019模型的计算值差异微小;在谱周期>0.16 s的范围内,XH2019模型的计算值大于本文所建模型的计算值,两计算值之间差异明显,且随谱周期的增加而逐渐变大,在谱周期为5 s时,XH2019模型的计算值远大于本文所建模型的计算值。

图11 本文模型与XH (2019)模型的计算值对比Fig. 11 Comparison of the DMF values in this paper with those predicted by Xiang and Huang (2019)

虽然本文与XIANG和HUANG均使用了日本俯冲带地震数据[30],认为震级因素与震源因素会对DMF值产生影响：一方面,XIANG和HUANG的研究中仅有1/3的地震数据含有VS30的信息[30],记录VS30的范围包括了110～1 270 m/s,其余数据则缺少VS30信息。并且按照VS30的数值划分六个区间,分别对比加速度谱DMF值与伪加速度谱DMF值在不同VS30区间内随谱周期的分布曲线后认为：VS30对T≥0.10 s的加速度普DMF值与伪加速度谱DMF值均无影响,VS30对T≤0.10 s的加速度普DMF值与伪加速度谱DMF值有较为明显关联,但在这一谱周期范围内难以发现VS30与DMF值之间的规律。所以不再考虑VS30对DMF值的影响;另一方面,XIANG和HUANG使用的地震数据中[30],震源深度最大超过了150 km,震源距离最远达到了526 km,未针对某一类地震选取相应的地震数据。因此本文推断产生以上差异的原因可能是由于XH2019模型未纳入VS30对DMF模型的影响,以及未划分地震类型进行研究所致。

4.2 对比张潇男等(2019)模型

利用本文模型对比张潇男等[21]在2019年建立的水平向加速度谱DMF模型,以分析同种地震类型下水平向DMF与竖向DMF之间的区别。

图12对比了各类场地中阻尼比为1%、4%、15%和30%时本文模型与张潇男等(2019)模型的DMF计算值随谱周期的变化。由图中可见：

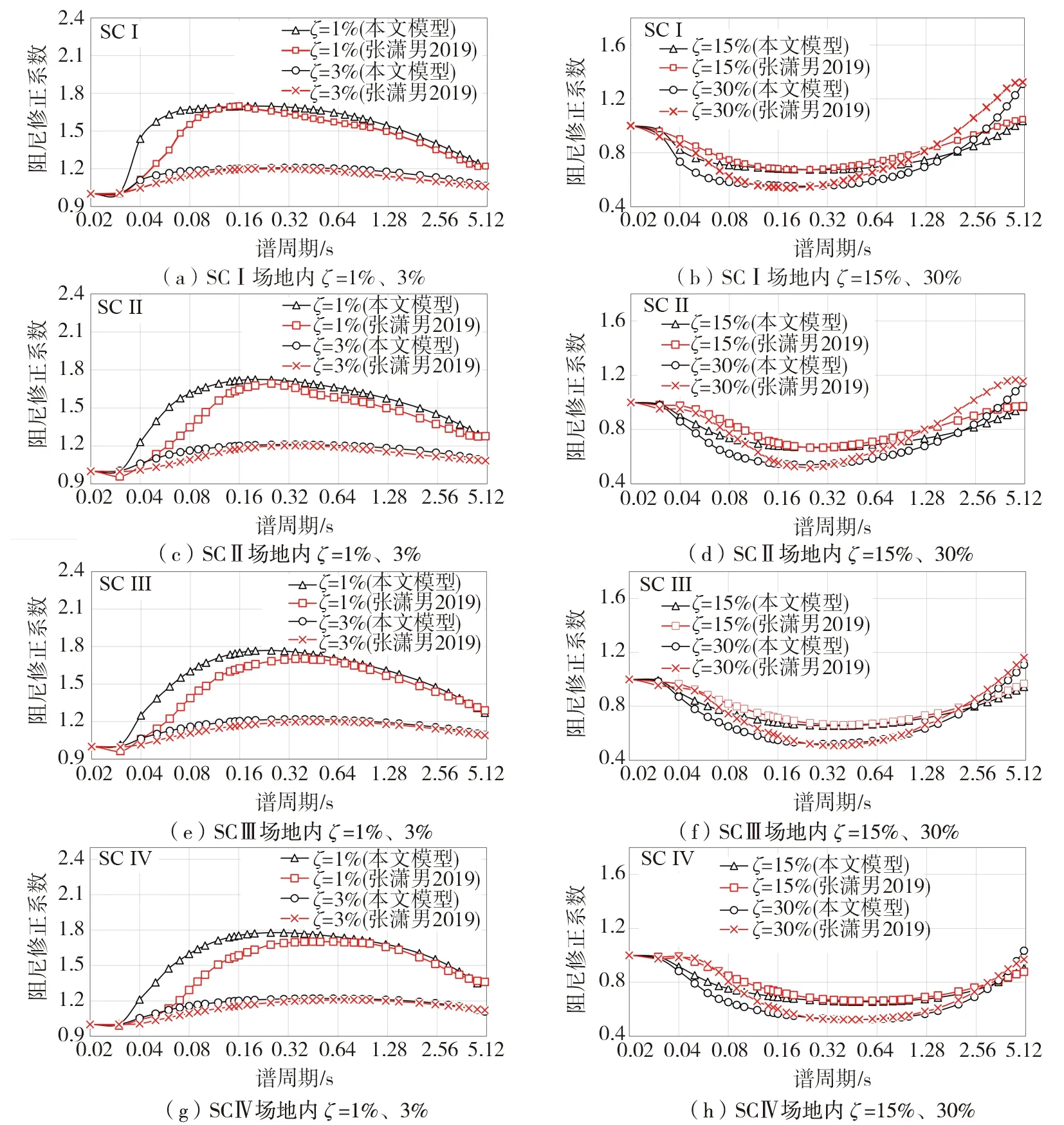
图12 本文模型与张潇男等(2019)模型Fig. 12 Comparison of the DMF values in this paper with those predicted by Zhang et al. (2019)

(a)水平向DMF模型曲线与竖向DMF模型曲线在不同场地类别、不同阻尼比下随谱周期的变化规律一致,在阻尼比小于5%的范围内模型曲线的峰值与阻尼比大于5%的范围内模型曲线的最小值出现的谱周期均随场地周期Ts的增加而增加,即峰值与最小值出现的谱周期SC Ⅳ>SC Ⅲ>SC Ⅱ>SC Ⅰ。

(b)在阻尼比小于5%的范围内,阻尼比越小,水平向DMF模型曲线与竖向DMF模型曲线差异越明显,在长周期范围内两者曲线基本相同,两模型间最大差距出现在SCⅠ场地,阻尼1%,谱周期为0.05 s处竖向DMF计算值为水平向DMF计算值的1.27倍。

(c)在阻尼比小于5%的范围内,以阻尼比1%为例,水平向DMF模型曲线与竖向DMF模型曲线交点位置所处的谱周期分别为SC Ⅰ场地0.15、SCⅡ场地0.28、SCⅢ场地0.64和SCⅣ场地1.25 s,随场地周期Ts的增大而增大,即曲线交点位置所处的谱周期SC Ⅳ>SC Ⅲ>SC Ⅱ>SC Ⅰ。

(d)在阻尼比大于5%时,水平向DMF曲线与竖向DMF曲线在SC Ⅰ场地与SC Ⅱ场地条件下只在某一小段谱周期内数值相近,在其他谱周期上,水平向DMF曲线数值均要大于竖向DMF曲线。而在SC Ⅲ场地与SC Ⅳ场地,两DMF模型曲线间的分布规律与阻尼比小于5%时相似,即在短周期内差异较大,随着谱周期增大,两曲线数值差距逐渐缩小,数值最终趋近相同。此现象产生的原因或与场地周期Ts的某一临界值相关,若进一步研究需对场地周期的划分方法进行改进。

通过以上对比可见：水平向加速度谱DMF模型与竖向加速度谱DMF模型不能通过某一固定参数实现两者之间的相互转换,或可通过建立与地震类别、场地类别、阻尼比和谱周期相关的方程实现。

5 结论

本文利用K-NET与KiK-net台站记录的3 552条俯冲带板间地震记录,分场地建立包含阻尼比与谱周期两个参数的竖向加速度谱阻尼修正系数模型,该模型适用于求解俯冲带地区无震源信息与路径信息下非5%阻尼比的竖向设计反应谱。利用随机效应法对模型的残差标准差进行分析,探究阻尼比和谱周期以外其它因素对模型的影响。最终得出以下结论：

1) 显著性检验表明阻尼修正系数几何均值有明显的场地差异性,需分场地建立对应的模型使计算结果更为准确。

2) 利用三次多项式方程建立的阻尼修正系数模型对阻尼修正系数的几何均值进行拟合,使各阻尼比与各谱周期下总残差标准差分布处于0.734以内,从而达到良好的拟合效果。

3) 由残差标准差的分析结果可知：事件间残差受矩震级与震源深度的共同影响,可通过向模型中加入反映震源效应的参数来提高模型精度;事件内残差主要受震源距的影响。由场地内残差与场地间残差的分析结果可知：分场地建立DMF模型可有效降低场地效应产生的误差,谱周期>0.16 s后,模型误差主要受路径效应影响,可通过向模型中加入反映路径效应的参数来提高模型精度。

4) DMF模型计算值在短周期内的误差主要受场地效应与路径效应的影响,在长周期和高阻尼比时震源效应引起的误差远大于路径效应与场地效应引起的误差。

5) 对比XH2019模型可见：两模型DMF拟合曲线趋势一致,但在小阻尼比、短周期,大阻尼比和长周期时两个模型计算值之间的差异显著,这可能是H2019模型未考虑地震类型与场地类型对DMF的影响所致。对比张潇男等(2019)模型可见：水平向加加速度谱DMF模型与竖向加速度谱DMF模型在短周期范围内模型的计算值差异显著,且两类DMF模型无法通过固定的参数值实现相互转换。