柔性格栅式防波堤消波性能试验研究

邹昊男 吴静萍 杨师宇

(武汉理工大学船海与能动工程学院1) 武汉 430063) (高性能船舶技术教育部重点实验室2) 武汉 430063) (中国船舶集团有限公司第七〇三研究所3) 哈尔滨 150078)

0 引 言

防波堤是一种为遮掩水域提供一个安全、稳定可靠的停泊和作业环境的海上消波装备.传统的坐底式防波堤从水底基础开始建造,因工程造价高、施工难度较大和阻断水质交换等因素而被水面式防波堤替代.相较于传统的坐底式防波堤,水面式防波堤具有低成本、运输便利、不受海底地质条件和水深的影响等优点,通常可以快速地为临时施工的水域形成一种安全、可靠、稳定的作业环境.通过对波浪能量分布的研究,人们发现深水波浪的能量主要集中在水面和水下3倍波高的区域.水面防波堤的消波主体主要位于水面附近,与波能分布特点相匹配[1],有效地利用了资源.新型水面式防波堤的研究一直受到了专家学者的关注.

目前,常见的水面式防波堤结构形式主要有浮箱式[2-3]、浮筒式[4-5]和浮筏式[6]等三种形式,虽然水面式防波堤形式多样,但对较长周期海浪(涌浪)的消波效果缺乏经济而有效的措施,还需要继续寻找更优的消波结构形式.

水面式防波堤主要通过波浪反射、波浪干涉、波能被转换或损耗消减波浪[7],在消减波浪时,消波主体的水平尺度和竖直尺度起关键作用.波长越长,尺度越大,如箱型浮式防波堤相对宽度超过0.35才能达到50%的明显的消波效果[8].然而,水面式防波堤通常采用钢筋混凝土等刚性材料建造,大型的消波主体不适合于灵活、临时使用,并且一旦在恶劣海浪中被毁坏将造成二次灾害.而柔性材料常用橡胶、合成材料和聚合物材料等,具有高强度的力学性能,质轻,适合大型建造,已经在不同的海洋装备中得到应用.柔性膜材料在水面式防波堤中,已经展开了诸如张紧的竖直柔性膜[9]和水平膜[10]、充满流体的柔性膜弹性囊、防波堤的柔性膜附体[11],以及框架形式等结构形式的研究和应用.

本文借鉴格栅在防风固沙上的成功应用,采用柔性材料制作格栅式防波堤, 采用柔性透明PVC板制作试验模型,格栅由直立方格组成.改变格栅模型宽度和浸深,改变方格边长,制作了6种模型,将模型固定在金属框架上,在小型推板造波水槽中展开试验研究.保持水深不变,保持模型出水高度不变,对6种模型展开了不同周期规则波和波陡的系列试验.讨论了格栅宽度、格栅浸深、格栅格子边长在不同波陡和波浪周期下的透射系数变化规律,试验结果表明:本文提出的柔性格栅式消波模型具有优良的消波性能.

1 模型试验

1.1 试验设备

本文物理模型试验地点在武汉理工大学流体力学实验室进行.小型波浪水槽全长18 m、宽0.6 m、高0.8 m,见图1.水槽的一端安装推板造波机,通过输入波浪参数远程驱动推板造波.水槽的另一端,为了尽可能减少池壁反射的作用,使水面快速恢复平静,水槽末端配有U形设计、放置多层缓坡透空板作为水槽消波段的消波装置.水槽壁面采用2 cm厚的钢化玻璃,方便观察试验时水槽内部发生的现象.

图1 波浪水槽照片

浪高仪为YWS200-DXX电容式数字浪高仪,最大量程为300 mm,测量绝对误差为±1 mm.

试验时,试验模型固定在水槽试验段,其中心距离造波板8.75 m,在模型前后布置浪高仪测量波面抬升.试验时水槽布置示意图见图2.

图2 波浪水槽试验布置示意图

文中物理试验时,布置4支浪高仪,沿着波浪传播方向分别以P1、P2、P3和P4依次命名.其中,P1和P2位于模型迎浪侧,用来处理反射波和反射系数;P3和P4位于模型去浪侧,用来处理透射波和透射系数.浪高仪P1放在距离造波板前缘6 m处,浪高仪P2距离模型中心1.75 m;浪高仪P3放在距离模型中心1.75 m处,浪高仪P4放在浪高仪P3后端1 m处的位置.

1.2 物理模型

采用柔性薄膜构造格栅,格栅的格子竖向贯通,格子水平面为边长S相等的正方形,在迎浪侧和去浪侧黏上两块有机玻璃板.固定安装的格栅模型见图3.

柔性薄膜为透明软质PVC材料,厚度1.5 mm,密度微大于水.有机玻璃板长56 cm、宽5 cm、厚5 mm,用胶水粘在柔性膜表面的上方,一方面减小柔性膜在波浪作用下的变形,另一方面辅助反射波浪.有机玻璃板和柔性薄膜材料见图3.

图3 柔性格栅模型安装图

铝杆构造的刚性框架固定在水槽上.钢片与柔性膜螺栓连接,将柔性格栅模型固定在框架上.另外,在固定试验模型的框架上方增加与水槽长度方向平行的铝杆,减小试验模型在波浪作用下发生的摇摆.

为了讨论模型宽度B、浸深d和格子边长S对柔性格栅消波性能的影响,设计了6种试验模型.模型尺度定义符号见图4,具体数据见表1.其中,模型M1和M2用于讨论模型宽度B的影响,M1、M3和M4讨论浸深d的影响,M2、M5和M6讨论格栅格子边长S的影响.模型统一露出水面1 cm,波浪翻越时加强波浪破碎,消耗波浪能量,增加消波效果.格栅模型在水槽宽度方向的长度尺寸均为58.5 cm.除了留出的与水槽壁面之间的安装缝隙,模型几乎贯穿整个水槽宽度.

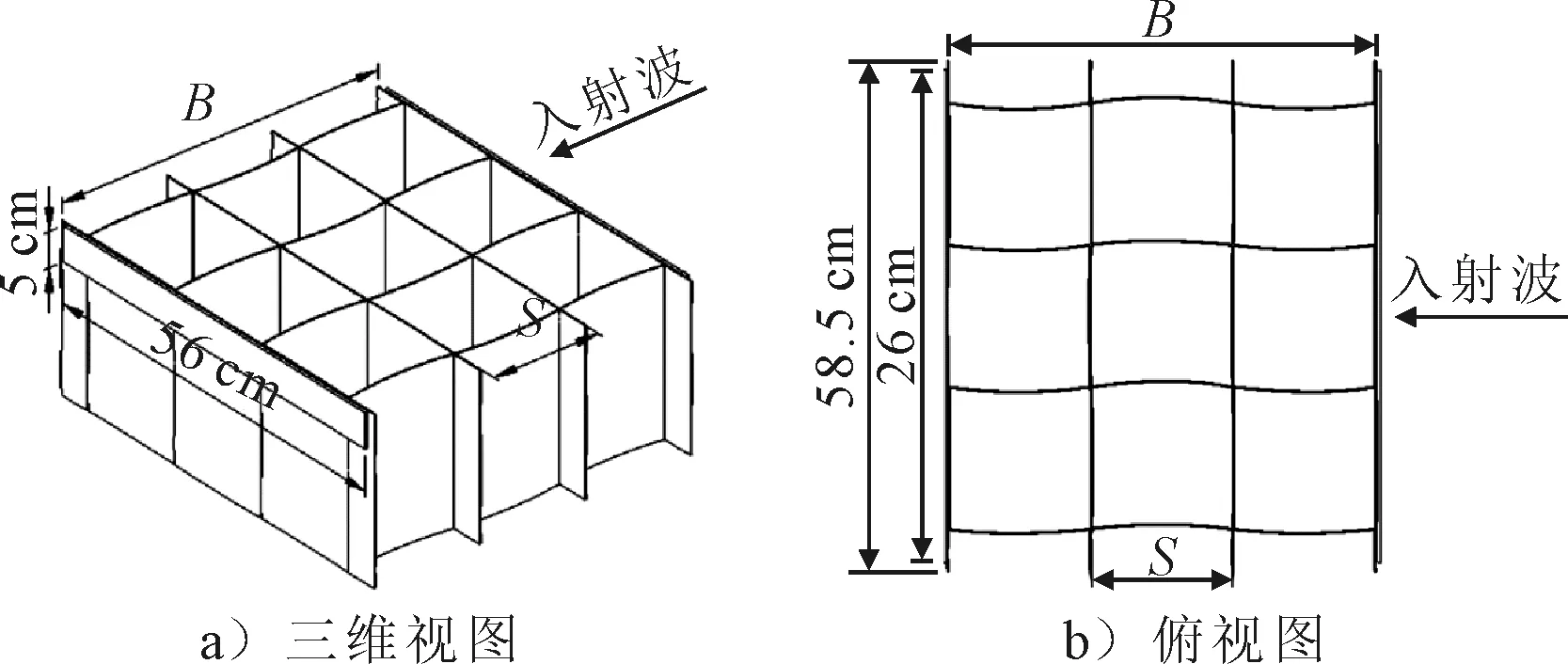
图4 柔性格栅模型示意图

表1 格栅试验模型的尺度 单位:cm

1.3 波浪参数

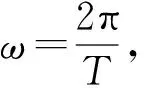
表2 波浪参数

1.4 透射系数处理方法

透射系数Kt是透射波高Ht与入射波高Hi的比值,即:

Kt=Ht/Hi

(1)

浪高仪P3和P4用来处理透射波和透射系数.实际使用P3,P4备用.入射波高Hi采用无模型时,浪高仪P3所测得的稳定波高H的平均值.透射波高Ht采用有模型时,浪高仪P3所测得的稳定波高H的平均值.计算式为

(2)

(3)

式中:N为所选取的连续稳定入射波和透射波波段中波高H的个数.由于本文的水槽长度和试验波长范围的限制,取N=3.实际测量波形和波高计算见图5.

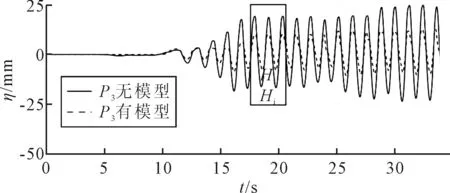
图5 浪高仪P3测量的波形和波高计算(T=1.2 s,H/L=0.02,Hi=35.42 mm,Ht=18.26 mm,Kt=0.52)

每次试验重复做了两次.由于水槽造波重复性很好,所以结果分析只采用其中一次.

2 试验结果分析

2.1 模型宽度B的影响

模型M1和M2的浸深d=11 cm,格子边长S=8 cm相同,但是它们的宽度B不同.M1的宽度B=40 cm,M2宽度B=48 cm.模型高度D=12 cm,出水高度为1 cm.

图6为波陡H/L=0.02, 0.05下,透射系数Kt随着无因次波浪参数kh的变化.

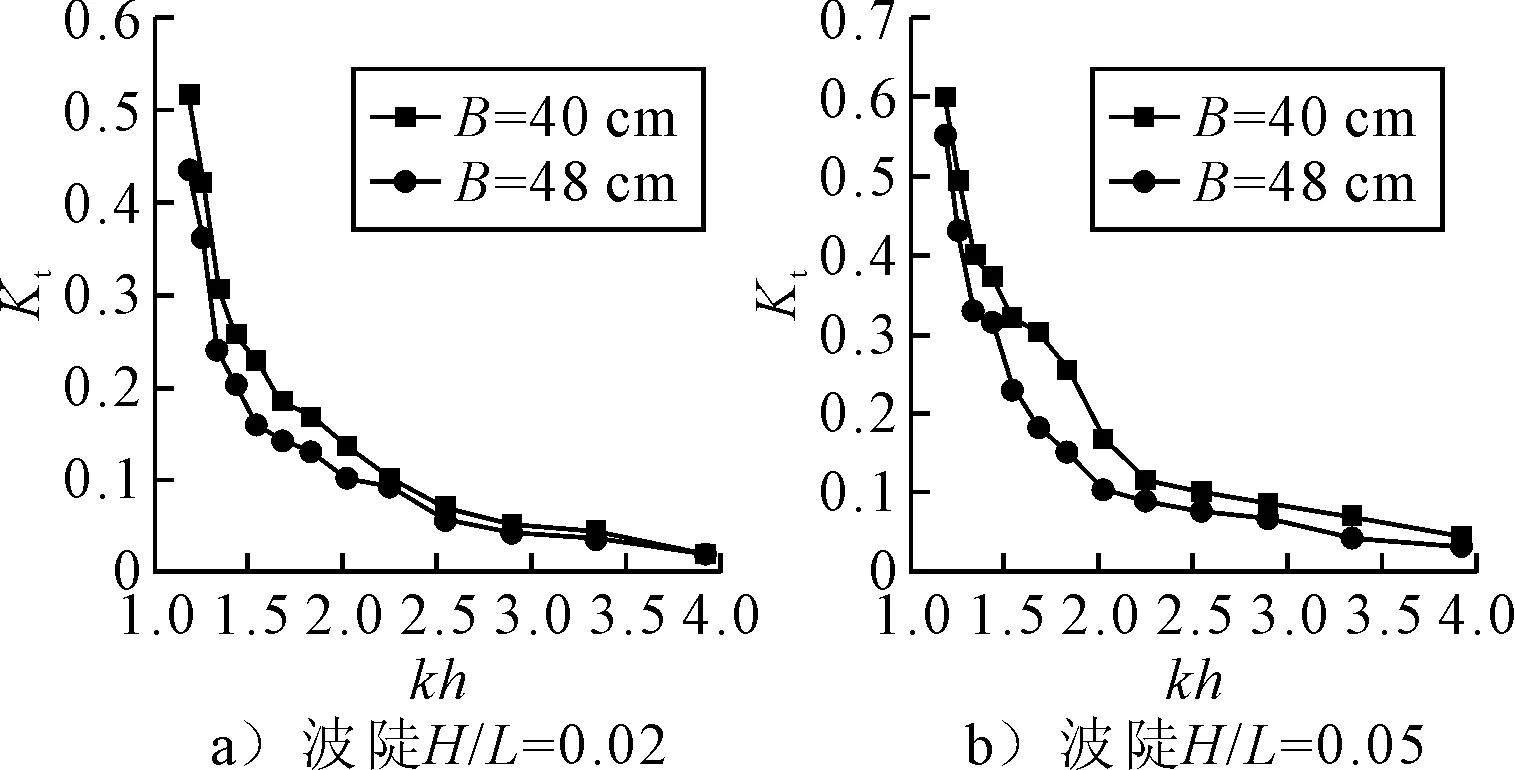
图6 模型宽度B对透射系数Kt的影响

由图6可知:模型M1和M2的透射系数Kt在波陡0.02和0.05下随着kh增加而下降的变化趋势大致相同,并且宽度B=48 cm的模型M2的透射系数Kt均小于宽度B=40 cm的模型M1.说明宽度越大,消波效果越好,这与水面式防波堤的消浪特性一致.另外,在kh>2.25的较小周期波情况下,模型M1和M2的透射系数Kt相趋于接近,说明此时模型M1和M2将小周期波几乎完全消减了.

2.2 模型浸深d的影响

模型M1、M3和M4的宽度B=40 cm,格子边长S=8 cm,但是他们的浸深d不同.分别为d=11,19,35 cm.它们的高度D也不同,分别为D=12,20,36 cm.出水高度均为1 cm.

图7为波陡H/L=0.05, 0.08下,透射系数Kt随着无因次波浪参数kh的变化.

图7 模型浸深d对透射系数Kt的影响

由图7可知:模型M1、M3和M4的透射系数Kt在H/L=0.05, 0.08下随着kh的增加均呈现下降趋势.浸深d=19 cm的模型M3的透射系数最小,而最大浸深d=35 cm的透射系数大于另外两种浸深较小的模型.这说明,柔性格栅消波装备存在最佳浸深,后续将进一步研究.发生这个现象的原因可能在于柔性体变形和摆动,以及波浪绕过模型底部的分离涡.

2.3 格子边长S的影响

模型M2、M5和M6用于分析格子边长的影响,格子边长分别为S=8,16,24 cm.宽度B=0.48 m,浸深d=11 cm,D=12 cm,出水高度为1 cm.

图8为波陡H/L=0.05下,透射系数Kt随着相对宽度B/L的变化.

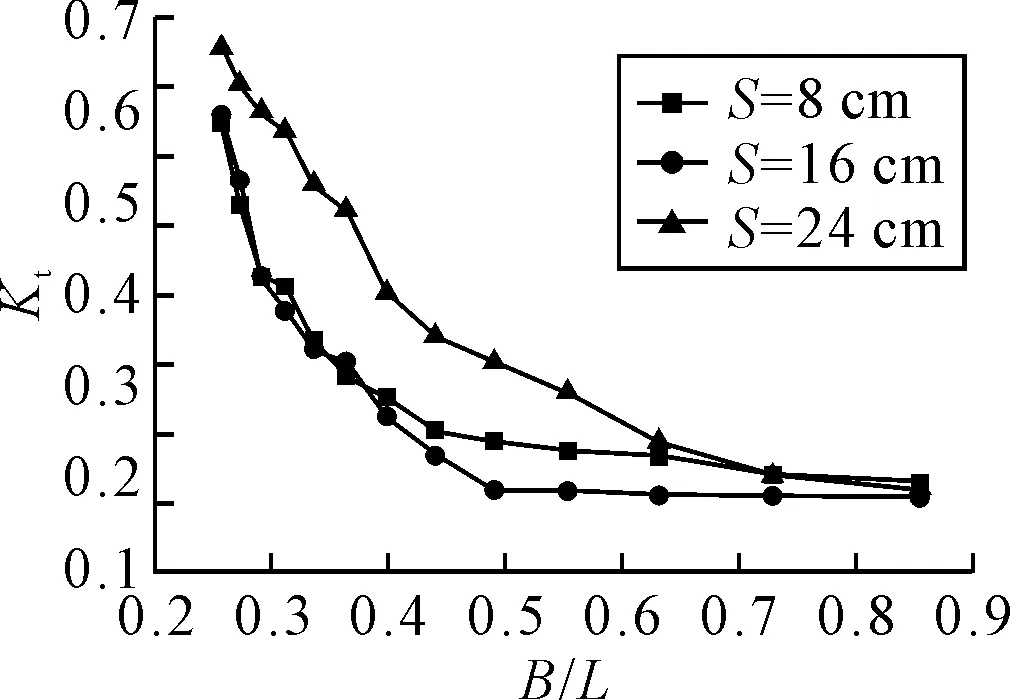
图8 格子边长S对透射系数Kt的影响

由图8可知:模型M2、M5和M6的透射系数Kt在波陡0.05下都随着B/L的增加呈现下降趋势.很明显,格子边长S=24 cm的模型M6的透射系数最大,消波性能最差;格子边长S=16 cm的模型M5的透射系数绝大多数B/L下是最小的.并且,格子边长S=8 cm,16 cm的模型M2和M5,当相对宽度B/L<0.4时,透射系数Kt曲线几乎重合,显示出相近的消波性能.

2.4 波陡H/L的影响

选取模型M1和M2分析波陡H/L的影响.两模型的宽度B不同,分别B=40,48 cm,其他几何参数一样,浸深d=11 cm,格子边长S=8 cm.

图9为模型M1和M2在波陡H/L=0.02,0.05和0.08下的透射系数Kt随着无因次波浪参数kh值的变化趋势.

图9 波陡H/L对透射系数Kt的影响

由图9可知:模型M1和模型M2的透射系数Kt在H/L=0.02,0.05和0.08下的变化趋势仍然大致一致,并且波陡大的都是系数完全大于波陡小的.这说明模型在大波陡的消波效果比小波陡的差,这与水面式防波堤的一般消波特性一致.

3 结 论

1) 增加模型的宽度B可以降低透射系数Kt,提升模型的消波性能.但是,当kh较大时,模型宽度对于透射系数Kt的影响较小.

2) 在一定范围内增加模型的浸深d同样可以降低透射系数Kt,提升模型的消波性能.但是,当模型触底时,模型的消波性能反而会变差.存在最佳浸深,后续进一步研究.

3) 在三个格子边长S中,两种较小的格子边长,消波性能比较接近,而最大的格子边长,消波性能最差.