内河无人船的自主路径规划模型研究

杨 娇 张庆年 杨 杰 吴绩伟 凌 强

(武汉理工大学交通与物流工程学院1) 武汉 430063) (武汉理工大学信息工程学院2) 武汉 430070) (上海国际港务(集团)股份有限公司3) 上海 200135)

0 引 言

自主路径规划技术是提高无人船自主决策能力的关键技术之一[1].常被分为局部及全局的路径规划,前者主要规划无人船与动态障碍物会遇时的避让路径,对模型的实效性、安全性要求更高;后者则主要避开静止障碍物等,对路径的经济性、安全性要求较高.

近年来,深度强化学习(deep reinforcement learning,DRL)逐渐成为驾驶决策新的研究方向,克服了通常智能算法需要样本数据的缺点,与传统路径规划相比,有更大的连续动作输出及较小的决策误差.Chen等[2]基于Q-learning的无人船路径规划方法,其可学习动作奖励并获得最佳动作策略.Shen等[3]提出了一种基于Dueling DQN算法的多船自动避碰方法,结合船舶机动性、船员经验和避碰规则来验证无人船的路径规划和避碰能力.Wang等[4]结合DDPG算法提出了一种USV航向跟踪控制方案,取得了良好的实验效果.Zhao等[5]采用近端策略优化(PPO)算法,结合船舶运动模型和导航规则,提出了多船的无人船舶自主避碰模型.能获得多艘船舶的时间效率和无碰撞路径,对未知的复杂环境具有良好的适应性.

这些经典的DRL方法中,DQN和Q-learning算法[6]均难以实现高维的连续动作.PPO算法采样效率较低,需要在每次梯度更新时采集新样本.而DDPG算法可解决连续状态行文空间下的DRL问题,结合了DQN算法具有经验回放池和目标网络的优点,但对超参数较敏感,最终策略次优甚至不能收敛[7].双延迟深度确定性策略梯度(twin-delayed deep deterministic policy gradient,TD3)算法针对深度确定性策略梯度(deep deterministic policy gradient,DDPG)算法的缺点做出三个关键性的优化,这使TD3算法的性能远远超过DDPG,故本文预先建立基于TD3的无人船自主路径规划模型.

1 船舶运动模型

采用地理坐标系和船体坐标系两个坐标系来描述船舶的运动.图1为船舶平面运动坐标系示意图,O0X0Y0为平面的上地理坐标系,OXY是平面上的船体坐标系.

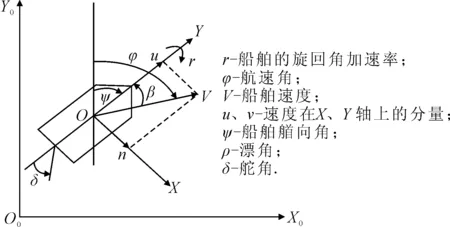
图1 船舶平面运动坐标系示意图

在图1中,两个坐标系之间的坐标转换为

(1)

船舶运动方程为

(2)

式中:(x0,y0,ψ)为无人船在地球坐标系的位置和航向;(u,v,r)为在船体坐标系下无人船的前向速度、横向速度及航向角速度.模型中考虑到船舶的操作性能时,可设置不同的参数训练模型.

响应模型中视船舶为动态系统,将船舶的各个部分视为一体,借助控制理论对船舶的运动进行分析.系统输出的首向角等与输入的舵角等参数之间存在动态响应关系.表达式为

TP+r=Kδ

式中:T为船舶追随性指数;P为r的一阶导数;K为船舶回旋性指数;r为旋回角加速度.K、T的计算见文献[8].

2 模型构建

2.1 TD3算法

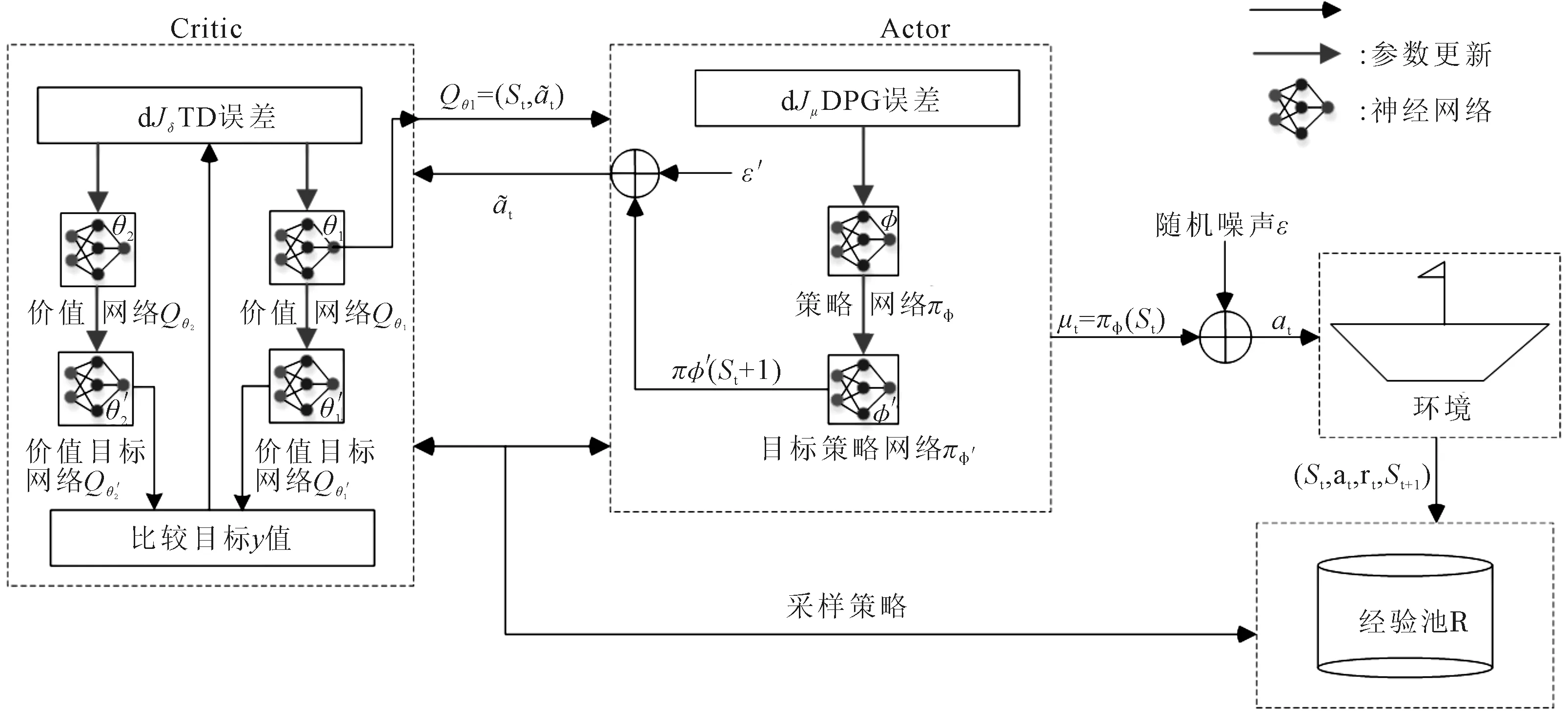
图2 基于TD3算法的无人船自主路径规划过程示意图

步骤1初始化价值网络Qθ1,Qθ2和策略网络πφ的参数θ1,θ2,φ.

步骤3初始化经验池R.

步骤4对每个周期episode,初始化状态s,循环以下步骤.

①根据当前状态st,选择动作并加入噪声:a～π(s|φ)+ε,ε～N(0,σ);

②执行动作at,得到奖励rt和新状态st+1;元组形式保存(st,at,rt,st+1)到R中;

③从R中随机选取m个样本;

④通过价值目标网络计算动作的期望回报:

c>0

⑥每隔d步,通过确定性策略梯度更新策略网络参数:

⑧结束此循环.

步骤5直到无人船到达终点状态或周期数达到设计值.

2.2 环境建模

在全局路径规划时,环境中的静止障碍物是已知的.为提高算法的效率,对不同的静止障碍物(含:礁石、水深不足、紊乱流态区、不可航区等)进行统一的简化处理.文中视任意不规则静止障碍物为多边形,然后计算任意两点的距离,见图3.取最大值为直径dm,取这两点的中点为圆心Om画圆.当无人船与Om的距离DOm≤min(1.5L,1.25L+dm)时(L:船长),则表示存在碰撞风险,环境将给予无人船惩罚.无人船通过与环境的不断交互,最终学会避开静止障碍物.

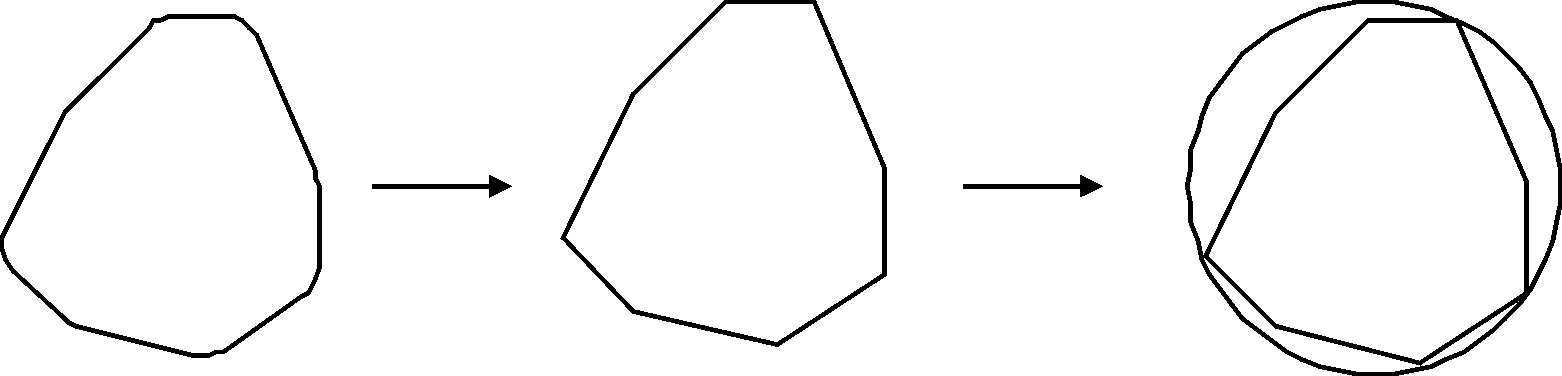
图3 静止障碍物处理示意图

2.3 模型结构设计

2.3.1模型结构

图4为基于TD3算法的无人船路径规划模型结构.模型通过获取的环境信息及船舶状态数据作为AC框架的输入状态.通过从经验池中随机抽取数据进行重复训练及学习,输出最优动作策略.无人船可在船舶动作控制器的帮助下避开障碍物并到达终点.

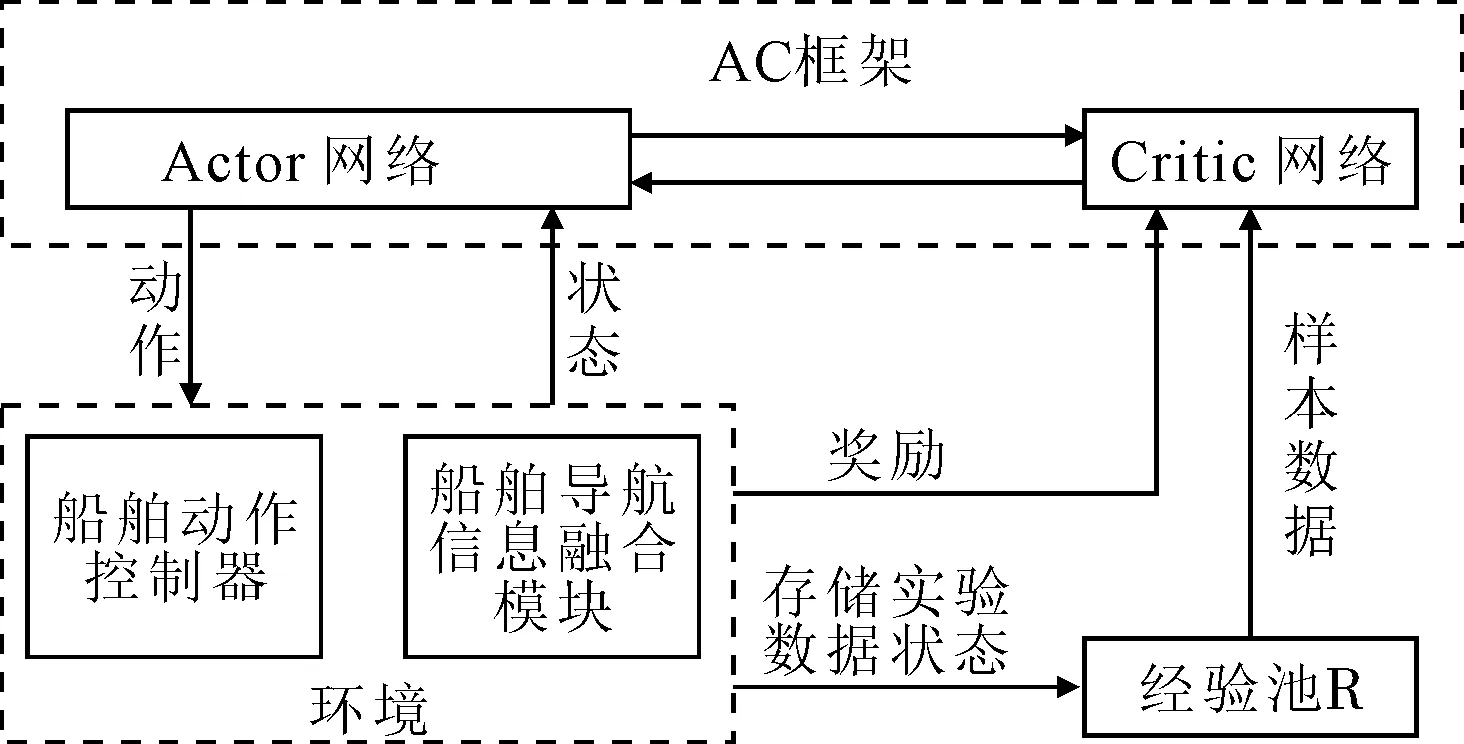
图4 基于TD3算法的无人船路径规划模型结构

2.3.2AC网络结构设计

Actor网络和Critic网络的输入参数为船舶状态数据,图5为AC框架的具体网络结构.

图5 AC框架的网络结构

TD3算法的六个神经网络中,Critic网络与Target Critic网络结构相同,Actor网络与Actor目标网络结构相同.其中,都包含了两个隐含层,且隐含层中均采用激活函数ReLU来控制输出范围.Actor网络中神经元的数量分别为300和600.Actor网络以船舶初始状态st作为输入,通过隐藏层后在网络的最后一层使用Tanh控制输出动作值范围[-1,1].Critic网络隐藏层神经元的数量均为200,在输出最终动作值Q时,不再用激活函数来控制网络输出结果范围.Actor网络输出动作的评价值称为Q值,用于评估Actor网络的输出动作.与Actor网络的输入参数不同,Critic网络以船舶初始状态st和Actor网络的输出动作at作为输入参数.

2.3.3状态空间设计

假设本研究中所需的状态信息均可由GPS、AIS、雷达等设备获取.将状态s定义为Agent在给定的单位时间步长t内所接收的环境信息.状态空间为s(x0,y0,V,ψ,xm,ym),其中,(x0,y0)为无人船的位置;V为航速;ψ为航向;(xm,ym)为障碍物圆心Om的位置.

2.3.4动作空间设计

无人船的行动策略主要包括行动控制及行动探索策略.在动作控制策略方面,Actor网络的输出动作之一用于指示转向aφ,Tanh激活函数用于控制输出范围,其值的范围为[-1,1],右边+左-.考虑船舶操纵性能约束,设Dmax表示单位时间t内的最大偏转角,取值范围为[0°,35°],Δφ表示船舶实际航向偏差值.计算公式为

Δφ=Tanh(aφ)Dmax

(3)

另一个输出动作是船速变量aV,Vmax是船舶速度变化的最大值,取值范围[-10,10]kn,增正减负.ΔV为船速的实际变化.计算公式为

ΔV=Tanh(av)Vmax

(4)

在动作探索策略方面,在输出动作中加入随机噪声以使无人船探索到更好的动作.定义随机噪声为

μ′(st)=μ(st)+Nt

(5)

式中:μ′为探索策略;Nt为添加的随机噪声.

采用Ornstein-Uhlenbeck (OU)方法作为无人船动作策略的随机噪声,它在连续动作空间有很好的效果,具体定义为

dxt=λ(μ-xt)+∂dWt

(6)

式中:λ为变量逼近平均值的速度;μ为动作均值;∂为随机过程的波动程度;Wt为Wiener过程.

2.3.5奖励函数设计

奖励函数是环境评估无人船动作优劣的反馈,正值为奖励,负值为惩罚.基于良好驾驶经验增加障碍物虚拟区以引导无人船可规划安全路径,当船舶与障碍物的距离DOo=max(1.5L,1.25L+dm)时设置障碍物区域,否则无.方法与对静止障碍物的处理方法相同.当船舶进入障碍区,环境就会对其进行惩罚.船离障碍物越近惩罚越大,反之越小.同时采用目标吸引策略,奖励与相邻时间船舶与目标的距离呈正相关.奖励函数设计为

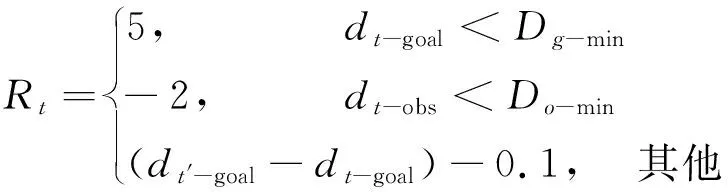
(7)

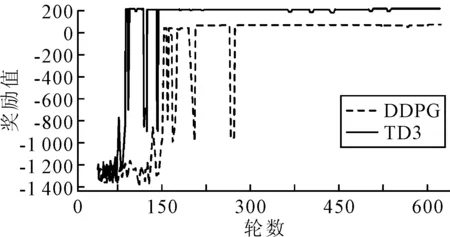
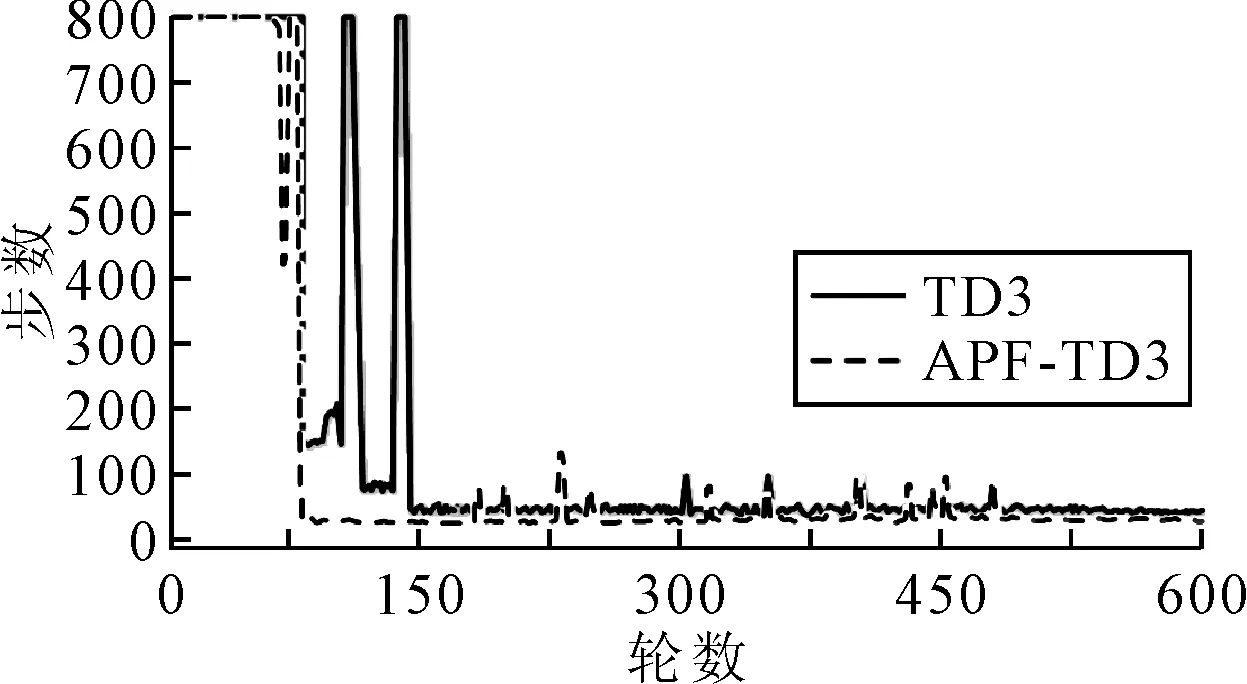
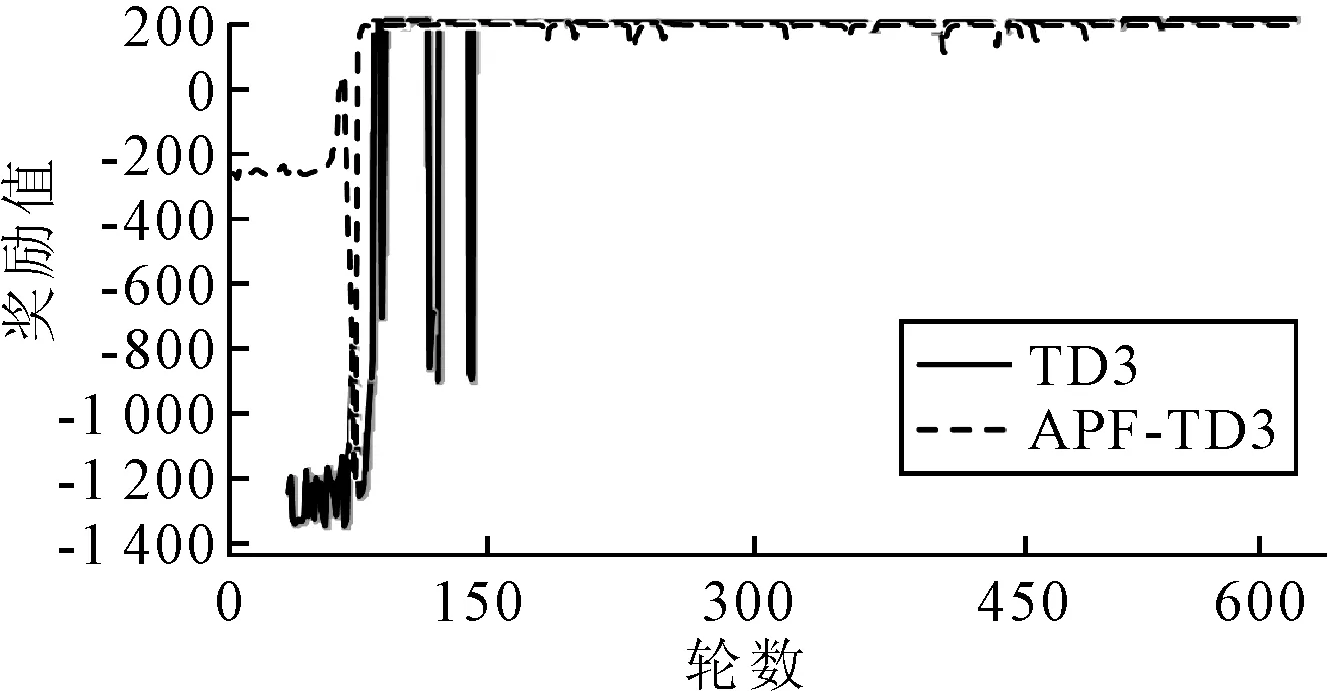
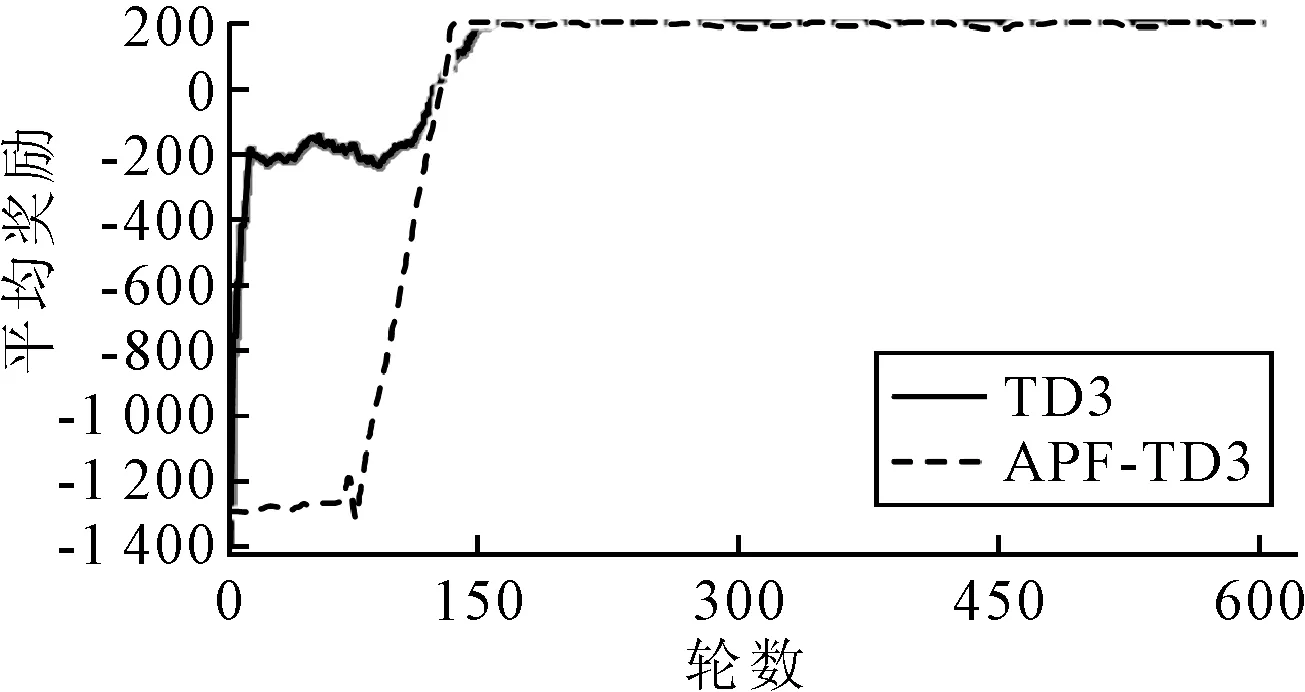
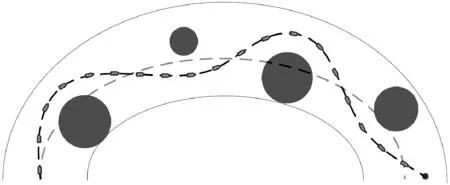
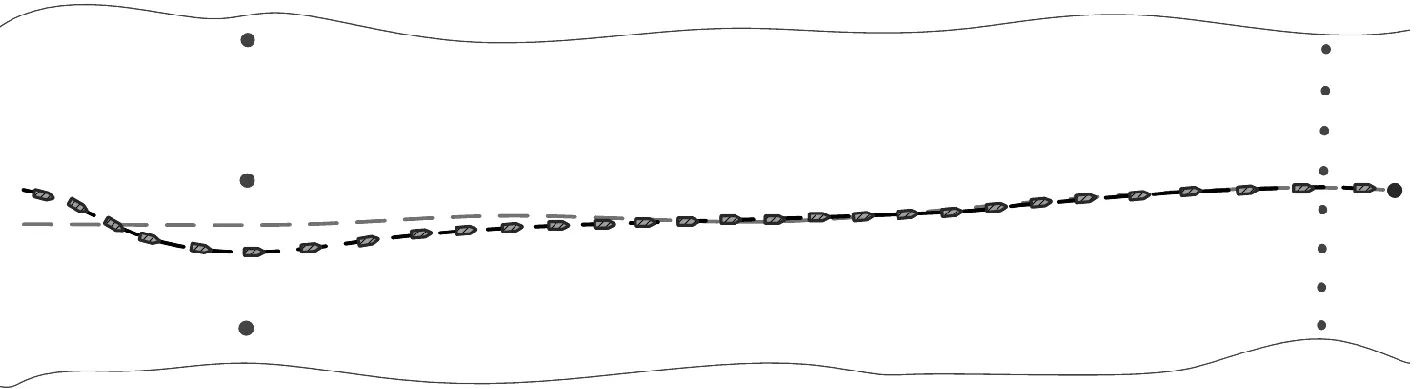
式中:dt-goal为当前时间t时船舶与目标点的距离;dt′-goal为前一时刻t′时船舶与目标点的距离;dt-obs为当前时间t船舶与障碍物的危险距离;Dg-min为船舶到达目标点的最小阈值;Do-min为船舶与障碍物的最小危险距离阈值.训练时,当船舶到达目标范围时,即dt-goal

3 模型训练仿真

3.1 模型训练过程

Actor网络和Critic网络都使用Adam网络优化器,其余参数见表1.控制变量对不同方法进行训练,获得训练步数、奖励和平均奖励.

表1 TD3算法用于路径规划时的参数

图6为无人船自主路径规划过程中TD3与DDPG两种算法每轮的训练步骤.由图6可知:TD3在约90轮时模型的训练步数达到最大,说明模型触发了训练的终止条件,没有实现路径规划或落入局部障碍区.从第95轮到第145轮,每轮的训练步数开始减少,平均训练步数维持在50步,表明无人船学习到越来越多的行动策略,自主规划完整路径.大约在第170轮之后,模型的训练步数保持在每轮45步以下,说明无人船已经充分学习到最优动作策略,没有碰撞风险.在第300轮附近,由于算法的探索性策略,训练步数增加,使得无人船尝试随机动作.而DDPG算法在170轮之后,模型的训练步数在100步左右.

图6 每轮步数

每轮累积奖励越大,学习效果越好.图7为模型每轮的累积奖励.在前60轮中,模型每轮的奖励较低,并且处理了波动状态,这表明无人船没有找到正确的路径,正在不断尝试新的行动策略.在第80轮左右,模型的奖励开始增加,表明找到了通往目标点的路径.第145轮之后,模型每轮的累积奖励趋于最大值,说明无人船已经找到了最优的行动策略.与图6相比,每轮累积奖励的趋势与每轮步数的变化一致.

图7 每轮累积奖励值

平均奖励反映了学习过程的效果,也更直接地观察了奖励的变化程度.图8为模型每150轮的平均奖励.

图8 每轮平均奖励

由图8可见:平均奖励值的总体趋势是增加的.大约在第15轮,平均奖励的增长速度开始放缓,然后逐渐趋于平稳.在第140轮之后,平均奖励趋于稳定,然后保持在一个较大的值,这表明该模型已经找到了此时的最优动作策略.

3.2 自主路径规划的改进模型

APF是一种虚拟引力场和斥力场的方法,目标点在虚拟环境中产生引力势场,障碍物在虚拟环境中产生斥力势场,引力场和斥力场叠加得到总场强.物体利用引力场接近目标点,利用斥力场避开障碍物,为

U(s)=Ua(s)+Ur(s)

(8)

式中:Ua(s)为s点引力场势能值;Ur(s)为s点斥力场势能值;U(s)为s点的势能.Ua(s)为

(9)

其中:ka为引力场的比例因子;ρg(s)为点s与目标的最小距离.

Ur(s)为

(10)

其中:kr为斥力场的比例因子;ρob(s)为点s到障碍物的最小距离,即ρob(s)为障碍物影响系数.

在无人船的路径规划问题中,奖励函数的稀疏性导致初始学习效率低和多次迭代等.因此,根据目标点和障碍点的位置信息构建APF.此时,势场中每个状态的势场值代表该状态si的最大累积奖励R(si),关系式为

R(si)=|U(si)|

(11)

式中:U(si)为在虚拟势场环境中状态si的势场值;R(si)为在状态si下采取最优行动时的最大累积奖励.基于APF-TD3的自主路径规划方法步骤如下.

步骤1根据虚拟环境中的目标点和障碍物构建势场,建立以目标点为中心的重力势场.

步骤2根据式 (11) 定义势能场中的势能值U(si)为状态si下的最大累积回报R(si).

步骤3船舶从起点开始探索环境,选择当前状态si下的动作.环境状态更新为状态st+1,并得即时奖励值r.

步骤4根据状态值函数更新Q值:Q(si,a)=r+γR(si+1).随后,更新在线Critic网络.

步骤5观察船舶是否到达目标点或达到设定的最大学习次数.如果两者满足其中一个,则本轮学习结束,开始下一次迭代.否则,返回步骤3.

当目标点位置加入重力场后,无人船更快到达目标点,动作策略的选择也更加稳定.基于APF-TD3的路径规划实验参数与3.1中的TD3算法参数相同.APF参数设置如下:ka=1.6,kr=1.2,ρ0=3.0.

图9为每轮步数.由图9可知:基于APF-TD3的每轮训练步数在第76轮开始下降并收敛,并且在后续的训练过程中波动,这是由算法的动作探索策略引起的.图10为每一轮的奖励值.基于APF-TD3的每轮的奖励值从训练到76轮开始增加,然后逐渐达到最大值,说明此时找到了更好的动作策略.图11为每轮的平均奖励值,基于APF-TD3的在第76轮开始时迅速增加然后稳定在最大值.

图9 每轮步数

图10 每轮累积奖励值

图11 每轮平均奖励

基于APF-TD3的每轮步数在第76轮左右开始减少.通过纵向对比两种方法,可以发现基于APF-DDPG的路径规划方法到达目标点的轮数更少,收敛速度更快,稳定性优于TD3算法.

基于APF-TD3的每轮奖励在第76轮开始增加并更快地达到最大奖励值.而基于TD3的在第80轮左右,模型的奖励才开始增加;在第145轮之后,模型每轮的累积奖励趋于最大值,无人船找到最优的行动策略.

基于APF-TD3的平均奖励在第76轮增加并更快地达到最大平均奖励值,比其他算法收敛得更快.实验过程的纵向比较表明,APF-TD3以最少的时间实现了最大的平均奖励,并且始终保持几乎不变.

3.3 路径规划模型仿真

3.3.1顺直河段

从船舶航行角度而言,顺直河段的航行条件是最佳的.此时航道宽度大、水深也大,可发充分发挥船舶的效率,所以在可保证安全时尽量提高航速.在此任务中,使用APF-TD3算法训练Agent避开静止障碍物并规划最佳路径.令点(50,400)为无人船的初始位置坐标,船长为100 m,航向为90°,航速为17 kn,令点(1 800,400)为目的地位置坐标.其中,最左边原点为起点,最右边原点为目标点,灰色实心圆表示障碍物,浅色虚线为水域主流线,箭头为船舶,深色虚线为规划的路径.仿真结果见图12.

图12 顺直河段仿真图

由图12可知:改进的模型在顺直河段中可以规划处光滑、安全、经济的航行路径.

3.3.2弯曲河段

弯曲河段航道受限、水深分布不均匀、流态紊乱,对船舶航行安全不利.同理,令点 (150,50)为无人船的起始位置,点(1 800,50)为目的地位置,航向为0°,航速为14 kn,其余保持不变进行仿真.仿真结果见图13.

图13 弯曲河段仿真图

由图13可知:规划得到的路径是以安全为前提的最小曲度的,同样,航线光滑度较好,经济性也明显.

3.3.3架桥河段

船舶通过桥区时,应提高航速以抑制与桥墩非正交的主流,避免船位偏移.起点为 (50,400),终点为(2 800,400),初始航速为15 kn,其他保持不变.仿真结果见图14.

图14 弯曲河段仿真图

由图14可知:规划得到的路径平滑,且在过桥时,提高了航速.同时,也充分的利用主流航行.

4 结 论

1) 量化内河良好驾驶经验,将其用于无人船全局自主路径规划模型中;其次历史经验数据的充分利用,也提高了算法的效率与准确率.

2) 基于APF-TD3算法的无人船路径规划模型可在已知环境中采取最佳、合理的行动,模型收敛快,精度高,规划的路径平滑无冗余.其成功完成内河无人船的全局路径规划任务,实现无人船端到端的学习方法.

3) 通过改进的无人船全局路径规划模型规划出的路径,可用于无人船的避碰研究中,作为避碰前后的航路,引导无人船避碰决策.